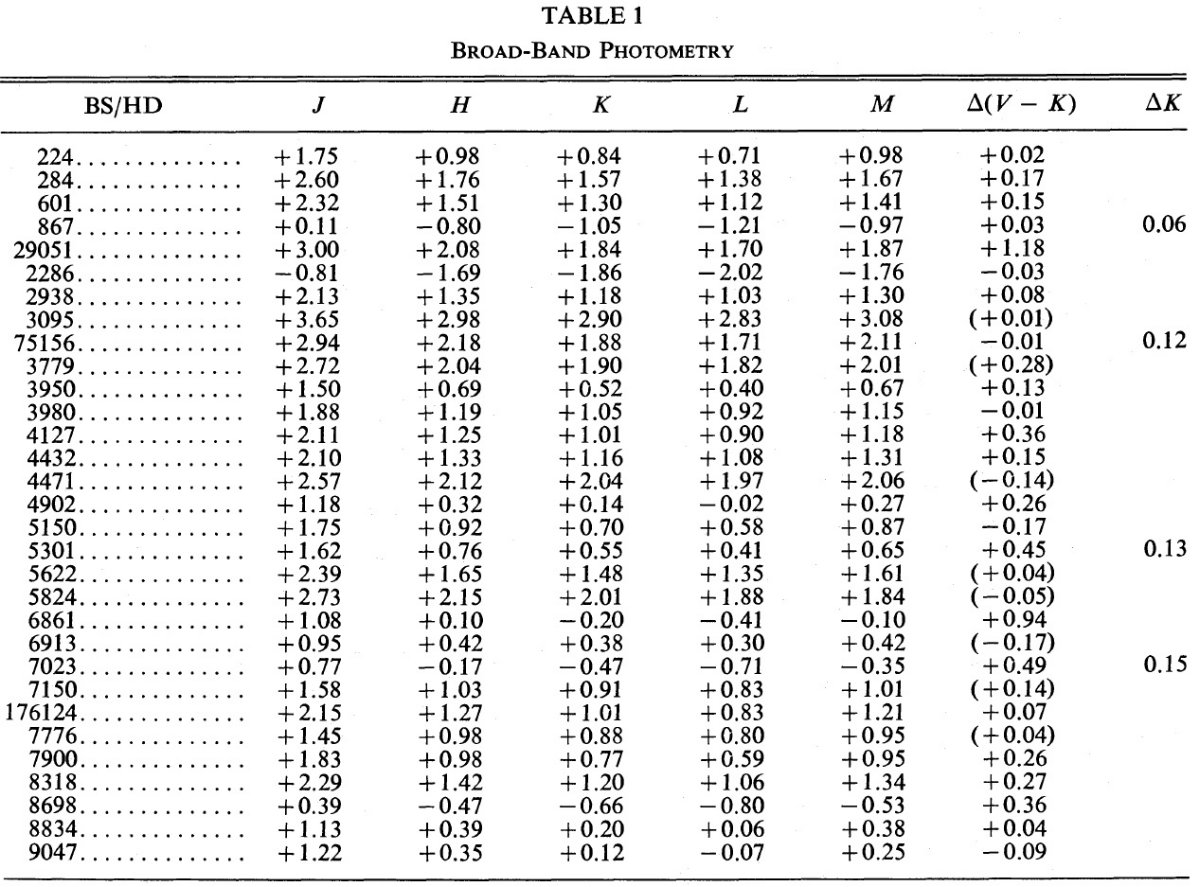
| 月掩蔽観測による角直径を赤外測光と組み合わせて K0 - M6 巨星の有効温度 Teff を求めた。Teff と 色温度、MK スペクトルタイプ、 V-K, I(104)-L との 関係を導いた。 | 主な結果として、低温側の巨星で Teff が以前よりも高くなった。調べた範囲 内で、最近のモデル大気との一致は良かった。 |
|
対象星 これまで、星の角直径の測定は数少なかった。しかし過去5年間に掩蔽観測から 62 星に対して 94 測定が得られた。19 星での複数回測定の結果は高い整合性 を示している。これ等の測定結果を用いて早期 K-型から中期 M-型の Teff 較正 を試みた。光度クラスは II, III とし、超巨星は除いた。超巨星の 赤化補正には不定性が大きく、したがってその固有カラーが怪しいからである。 その上、星周層の散乱や球状性効果 Tsuji 1978b などで測定された角直径が 光球を表しているかどうかが疑問となる。また、ミラ型星も除いた。我々の リストには5個の変光星が含まれるが、本質的には非変光星を扱う。 |
温度スケールを上げる これまでにも温度スケールを上げる必要があることは示唆されていた。Hayes 1978 は掩蔽観測結果から、M0 - M4 で Johnson 1966 よりかなり高い有効温度 を提唱した。我々の集めた新しい測定結果は M-型星温度が以前信じられていた より高いことを示す。実際それは Hayes の温度スケールよりも上に来る。 |
|
α Sco 掩蔽 41 milli-arcsec Evans 1957 40 Pease 1931 スペックル 42 Labeyrie, Stachnik 1972 干渉計 42 Braunstein 1978 この星の角直径が大きすぎるので掩蔽には不適当なケースである。 α Leo α Leo B7 V は 強度干渉計 1.3 Hanbury Brown, Davis, Allen 1974 掩蔽で測れる限界に近い。1980 年に掩蔽が起きる。 |
μ Gem μ Gem は M3 III 星である。その角直径は 掩蔽 12 milli-arcsec Ridgway, Wells, Joyce 1977 干渉計 14 Braunstein 1978 α Tau α Tau は 現在掩蔽を繰り返しており、将来の解析が有望である。 掩蔽の最適な大きさ 掩蔽の最適な大きさは 3 - 12 milli-arcsec である。しかし、現在他の手法の データが少ないので比較ができない。 |

|
輻射補正は不正確 通常、輻射等級を求めるには、可視等級に星のスペクトル型に対応する輻射 補正を施すのだが、この方法は特に低温度星に対しては大きな誤差を生む。 有効温度が低くなると、輻射補正の値が大きくなり、かつスペクトル型に敏感 になるからである。したがって、スペクトル型を正確に決める必要があるし、 さらに同じスペクトル型に対する輻射補正値の散らばりが大きい可能性がある。 この論文では、したがって多バンド測光結果から輻射等級を直接求める。 多色測光 KPNO 1.3 m 鏡で JHKLM 測光を行った。表1にその結果を示す。表3には それらの別名も載せた。UBVRI 等級は Johnson et al 1966, Barnes, Evans, Moffett 1978 などから集めた。短波長側、長波長側はスペクトル を外挿して総フラックスを台形積分した。 色超過の指標 Δ(V-K) 表1には色超過の指標 Δ(V-K) を載せた。これは観測 (V-K) カラーと スペクトル型に対応する星の平均カラー(Johnson 1966) との差である。可能な 場合次章で述べる狭帯フィルター測光からのスペクトル型を使用した。分光から 決めたスペクトル型を用いた場合には Δ(V-K) に括弧を付けた。 |
色超過 E(V-K) Δ(V-K) は色超過 E(V-K) とは違う。なぜなら、光度クラスやメタル量 の影響(おそらく)で (V-K) とスペクトル型との関係には散らばりがあるはず で、かつサンプル星は近いので赤化が起きるとは考えにくいからである。実際、 Δ(V-K) が負のサンプルも存在する。Δ(V-K) > 0.2 の場合に のみ、Δ(V-K) = E(V-K) と考え、それ以下では E(V-K) = 0 とする。 |
|
狭帯8色測光の用途 角直径測定から導いた有効温度の主なる用途は(スペクトル型、Teff) 関係 の確立である。この理由で我々は狭帯8色測光 Wing 1971, White, Wing 1978 によるスペクトル型とブランケッティング・フリーな色温度の取得に重点を 置いている。このシステムは K3 より晩期型でスペクトル型の2次元分類を 与える。7100 A 付近の TiO 吸収は温度クラスを与え、その精度は写真分光 による分類より遥かに高精度である。CN バンドは光度クラスにも鋭敏であるが、 化学組成にもよる。 カラー温度 8色測光の較正済み 8000, および 10,500 A 付近でのフラックスに黒体輻射 をフィットして色温度が得られる。これらの色温度は分子、原子ブランケッテ ィングの影響を通常の広帯カラー V-R, R-I より受けにくい。 |
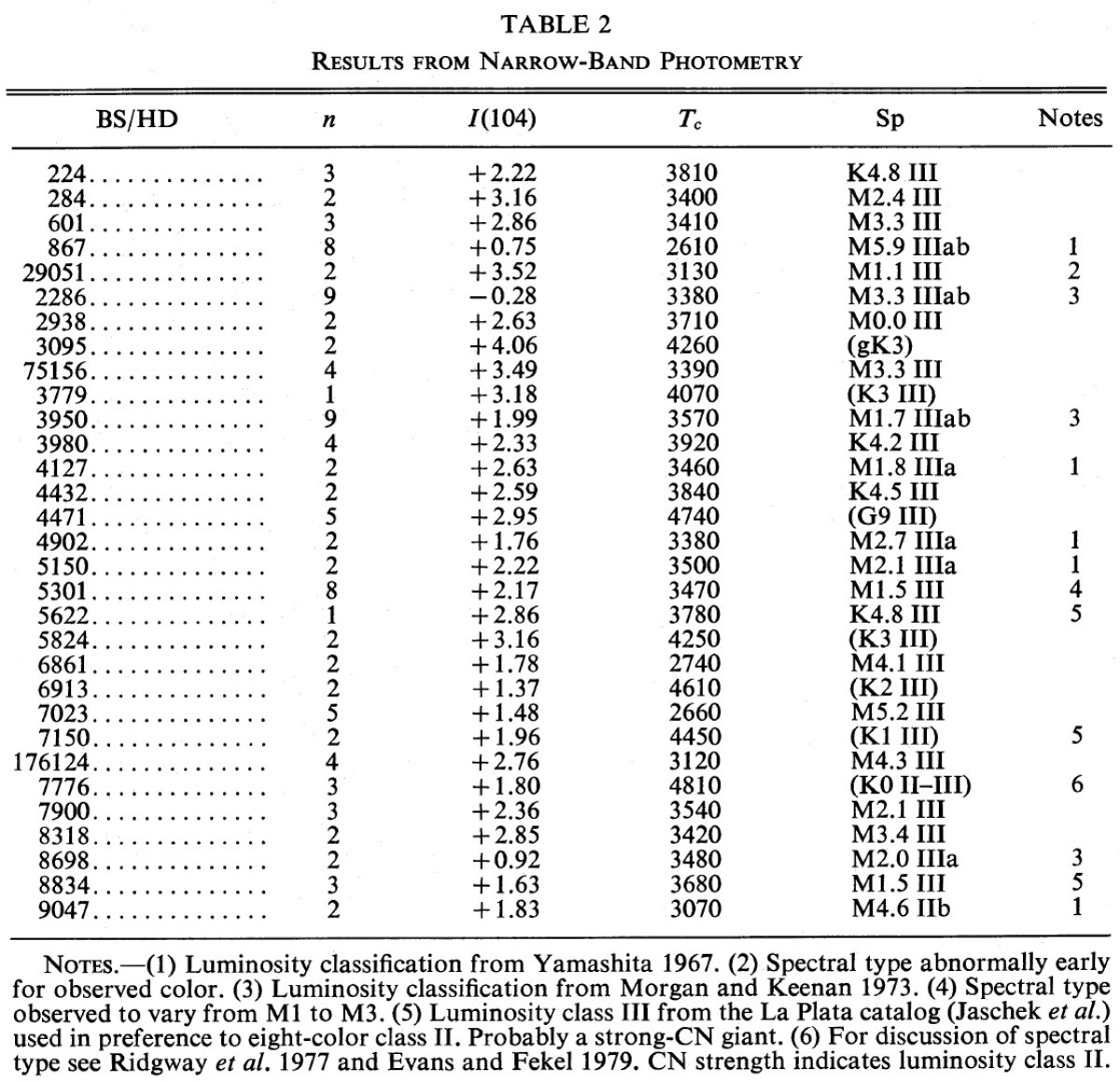
8色測光分類 8色測光データの一部は Wing 1978 から、残りは KPNO と ローウェル天文台 での観測から得た。結果は表2に示す。 I(104) は 10,400 A で測られ、 ベガでゼロ等とした。Tc = カラー温度である。スペクトル型は8色測光から 決めたが、例外として (1)K3 より早期型は TiO バンドを欠くので、スペクトル型は他文献から。 (2)CN 強度による分類よりも原子線の吸収による分類(MK-分類)を優先する。 8色測光は クラス II の通常 CN 強度の巨星と強い CN 強度のクラス III 巨星 を区別できないからである。星によっては測光から得た温度クラスを文献の MK 光度クラスと併記した。 |
|
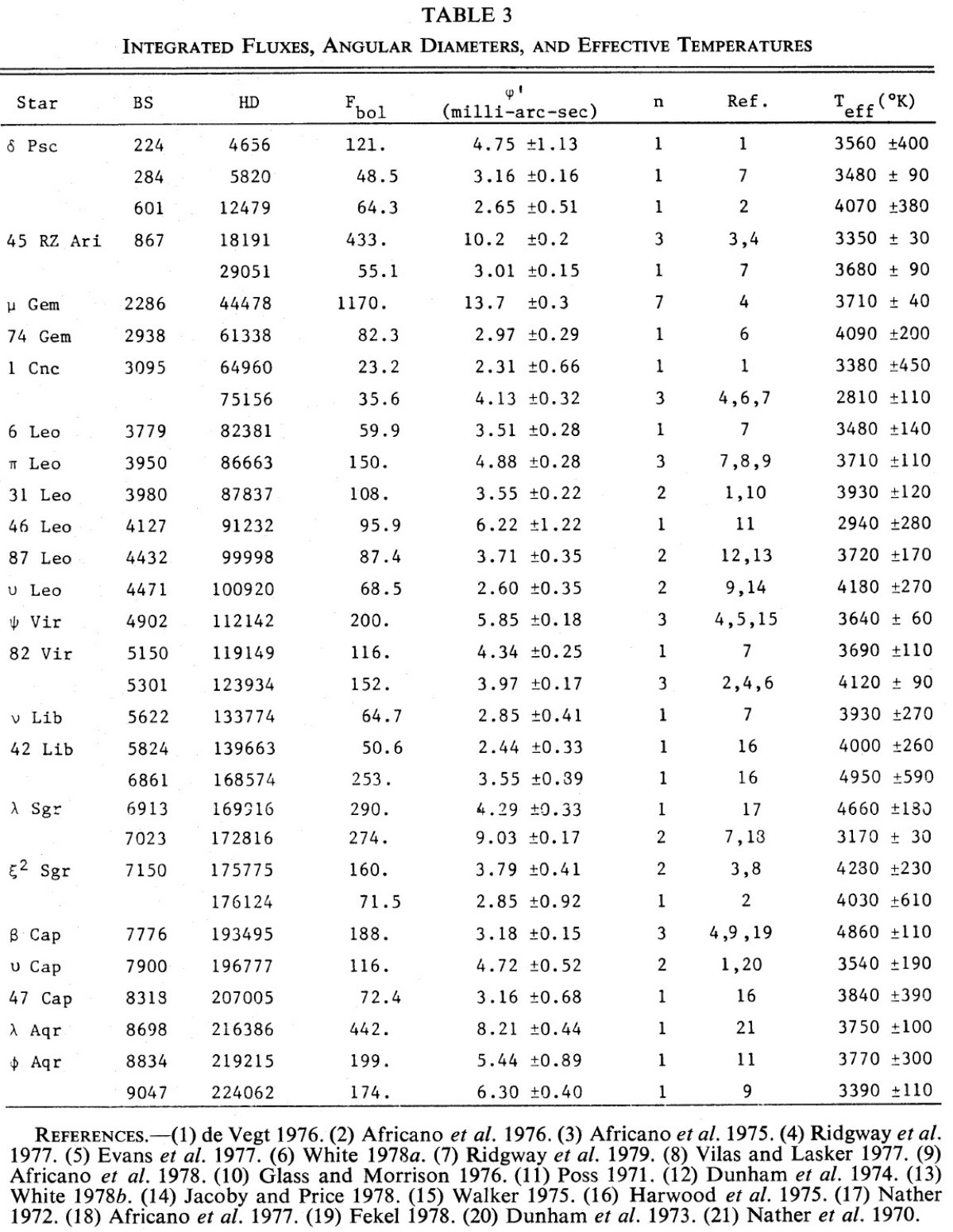
有効温度の定義 有効温度 Teff は次の式から決める。 F = (φ/2)2σTeff4 計算に便利な表記にすると、 Teff = 2341(Fbol)1/4/(φ')1/2 ここに、Fbol は 10-8 ergs cm-2s-1 を単位とし、φ' は milli-arcsec 単位である。 リムダークニング "fully darkened disk" の直径は "uniform disk" の 1.13 倍である。 リムダークニングの効果を Ridgway, Wells, Carbon 1974 が計算した。 |
1.6 μm 視直径 オパシティの波長依存性のため、視直径は波長により変化する。特に、 1.6 μm 吸収極小における視直径は可視直径よりも小さい。 その効果は 3 % 程度で、Teff に 50 K の変化をもたらす。 物理的にはエネルギーピークに近い 1.6 μm 視直径を採用すべきである。 ただし、モデルの欠如等の理由でここではその補正を行わない。 輻射等級 リムダークニング補正ファクターを用いて文献にある視直径を直した。 修正した視直径は表3に示す。この表で n = 独立な測定回数である。Fbol の単位は前に述べた。Fbol と輻射等級との関係は、 mbol = -2.5 log Fbol + 8.5 である。 |
|
図1= Teff-Tc 関係 表3の視直径のエラーが有効温度で 250 K 以下に収まる星が 20 個ある。 図1にはそれらのみを使った Teff - Tc 関係を示す。Teff ≤ 4000 K, M-型星は系統的に Teff = Tc を表す破線より上にずれる。実線=データに フィット、を描くに当たり、以下に留意した。 (1)M2, M3 (Teff = 3500 - 3700 K)の質の良いデータ点の中央を通る。 (2)最低温の 45 Ari と BS 7023 を通る。 (3)高温部では漸近的に Teff = Tc になる。 図2=エラーの大きなデータ 図2にはエラーが 250 - 700 K の低精度データを示す。明らかにこれらは 温度較正に使用不能である。 低温側での乖離 図1の著しい特徴は低温になると Teff が Tc から離れていく傾向である。 ラインブランケッティングや連続吸収の効果で、短波長がわでは明らかにフラックス が抑えられている。例えば M0 - M6 星では 7540 A 中心の 50 A 巾フィルター。 これが Tc を低く見せている。その原因ははっきり分からない。非常に低温の 星では VO 吸収がこのバンドに現れるため M7 より晩期型星では 8 バンド 測光の Tc が非常に低くなる。しかし、その効果は M0 - M3 では小さいだろう。 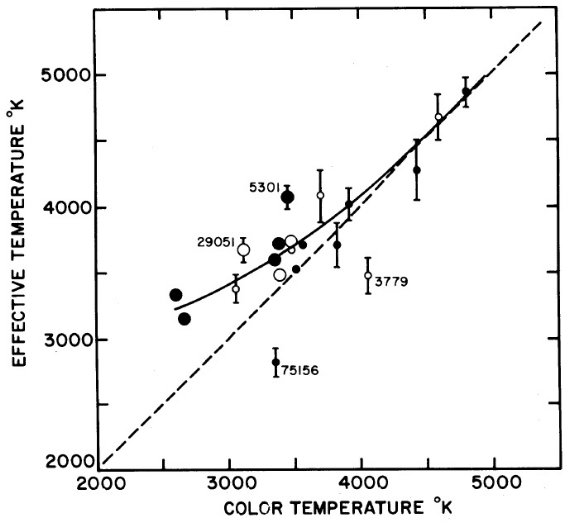 図1.表3からの有効温度と表2からの色温度の関係。大丸 = 1σ エラー 100 K 以下のデータ。小丸 = 1σ エラーが 100 - 250 K データ。黒丸 = 数個の独立測定存在。実線=適用較正曲線。破線は1 Teff = Tcolor.数字は HD 又は BS 番号。 |
この領域には原子吸収線は殆ど存在しない。低温になると自由電子数が減少
するので H- 吸収強度は逆相関になる。また、C は CO, N は
N2 に取り込まれるから CN も逆相関である。TiO 線吸収は
温度依存性は合っているがこの波長帯に TiO 吸収線がない。
フィットに乗らない星 乖離の原因は不明だが、図1の乖離自体は実際に存在すると考える。 考え得る原因は先に検討した効果の複合かも知れない。Tc のエラーは 30 - 40 K と小さく、図1のエラーの主原因は視直径の測定にある。 しかし、いくつかのおかしな星も存在する。 BS 5301 は Teff = 4120, Tc = 3470 でフィット線から外れている。この 星の測光データ、視直径測定は数回行われ整合している。しかし、スペクトル 型には変動が見られ、スペクトル型変動星らしい。 HD 29051 の場合 Teff = 2819 K, Tc = 3390 K で 実線を大きく 800 K も 下回っている。 HD 29051 の場合、色温度とスペクトル型が合わない。 Tc = 3130 K は M4 を 示すが、スペクトル型は M1.1 である。V-K カラーもスペクトル型からの予想 値より赤く、Δ(V-K) = 1.18 となる。以前に決めた手続きに従うとこれは 赤化のためとするのだが、この星がヒアデス付近にあることを考えると 無理がある。 Tc - Teff 関係の有用性 以上のような特異例は存在するが、一般には Tc - Teff 関係は 良い。この関係を使えば 8 バンド測光から決めた Tc から Teff を決められる。 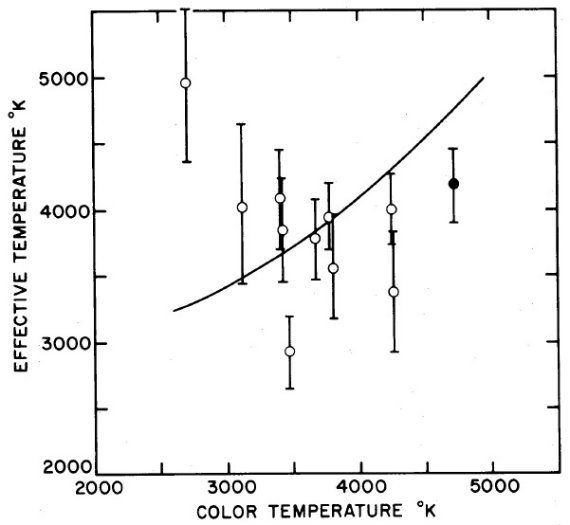 図2.図1と同じだが、 1σ エラーが 250 K より大きいデータ。 実線は図1から採った。 |
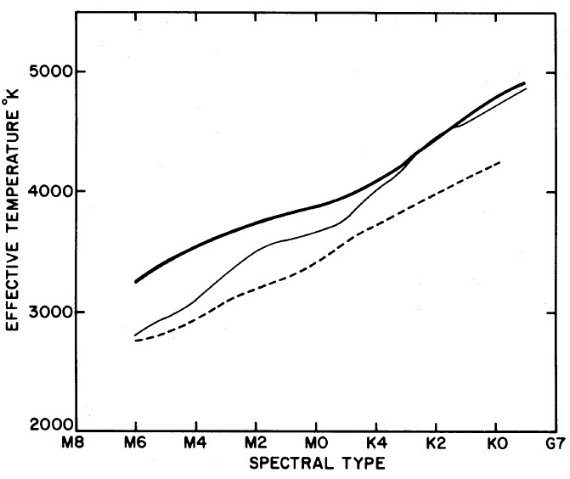 図3.太線=図1の Teff - Tc フィットを (Teff, MK スペクトル型) に 変換。細実線=Johnson 1966 の Teff 較正。破線= Kuiper 1938 の Teff 較正。 |
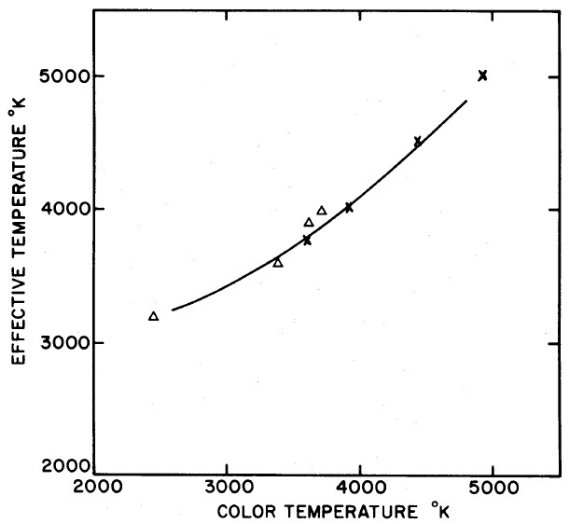 図4.図1の (Teff, Tc) 関係を最近の二つと比較。 x 印= Bell et al 1976 のモデル。△= Tc 既知の4巨星の Teff (Tsuji 1978) |
|
Teff - B-V 関係 Teff - B-V プロットは B-V = 1.6 の周りの散らばりとなり、 観測点は Flower 1977 がモデルから出したラインを再現しない。 温度指標としては役に立たない。 V-K B-V よりは役に立つ。V フィルターは TiO バンドを含む。この吸収帯は 通常の巨星では温度に鋭敏で V-K を増加させる。しかし、例えば球状星団巨星 Mould, McElroy (1978) のように (Teff, TiO) 関係が異常な例には適用不能である。 温度指標の条件 カラーが温度指標として最適であるためには、 (1)二つのバンド内に線吸収がない。 (2)似たような連続吸収。 (3)しかし、異なる温度依存性。 非常に低温度の星で以上を満たす波長帯として、Johnson 1966 は I-L を推奨 した。I バンド内の TiO 吸収を避けるために Dyle et al 1974 は I (104)-L を用いた。I (104) は8カラー測光系の等級である。このカラーは辻 1978a が観測フラックス分布にモデルをフィットする際に用いたものと大体同じで ある。λ < 1 μm での分子ブランケッティング効果を避けるため、 辻はフィットの重みを 1 μm 付近と 2 μm より長波長側に掛けた。辻の Teff は I (104)-L または I (104)-L と緊密に関係するはずである。 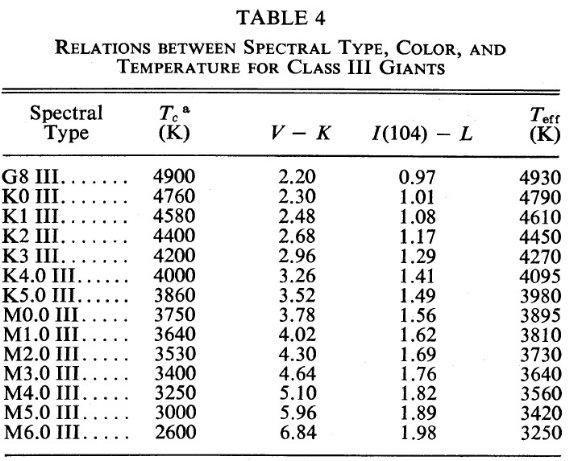 表4.クラス III 巨星のスペクトル型、 Tc, カラー、Teff |
図5= Teff - V-K または I (104)-L 関係 図5に示した Teff と V-K, I (104)-L との関係は図1に示した Teff - Tc 関係を既知の Tc と V-K, I(104)-L 関係 (表4)でつないだものである。 二つのカラーのスケールにはファクター5の違いがあることに注意せよ。 V-K はサブクラス1毎に 0.35 mag の変化を示し、温度変化に対し大変敏感で ある。一方 I (104)-L は サブクラス1毎に 0.07 mag で変化は小さい。しかし、 元素組成が不明または通常でない星に対しては、前に述べた理由により、 こちらの方が安定して使える。 表4=スペクトル型、カラー、色温度、 有効温度関係 スペクトル型、カラー、色温度、有効温度の間の 関係を表4に示す。これは Wing, Ridgway 1979 の結果である。初めの4列の 数字は測光値だけから得られる量なのでよく決まっている。有効温度は Tc の 関数として図1から採った。これらの関係は太陽組成で光度クラス III の巨星 に当てはまる関係である。 ( 表4のスペクトル型・有効温度 関係はAQには採用されていない。現在の定説値は何だろう?) 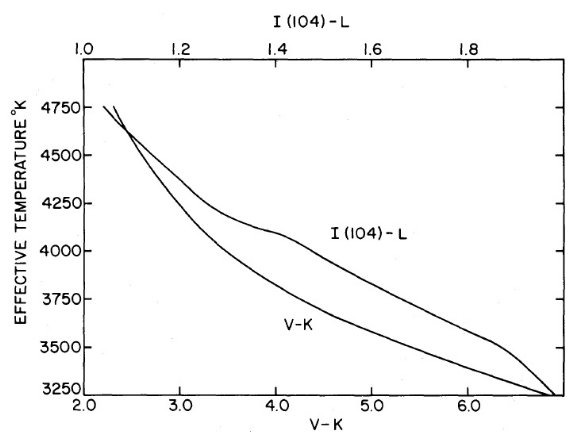 図5.図1の (Teff, Tc) を (Teff, V-K), (Teff, I(104)-L) に変換。 |
|
3つの大きな影響 有効温度較正は多くの分野に影響するが、特に次の3つは重要である。 1.HR図上の赤色巨星 HR図上の赤色巨星位置を研究するにあたって、今後は中間 M-型星 (M4 - M6) 有効温度が 450 K 高いことを考慮する必要がある。辻 1978 が述べているように、 低温度星温度の上昇は非常に晩期型の巨星の進化上の問題を軽減する。 更に興味深い問題はより低温度の星、特に非ミラ型星、の Teff 較正である。 |
2.化学組成 多くの分光研究が現在も (Teff, スペクトル型) 関係を使用している。組成 決定に必要な吸収線の多くが温度に鋭敏なので、温度スケールに系統誤差がある とそれが組成に反映される。例えば、温度に間違いがあると H2O バンド強度から 出す C/O 比が変わる。 3.低温度巨星の大気構造 低温度巨星の大気構造を研究する際には温度の値は重要なパラメタ―である。 例えば、 Ramsey 1977 は電離平行に及ぼす non-LTE 効果の影響を研究した が、 Carbon 1979 によると有効温度が上昇すると見かけ上の non-LTE 効果 が減少する。 |
|
辻と合う 新しい有効温度の決定は K0 - K3 では依然と同じとなったが、M0 - M6 では著しく高い結果になった。これは定性的には辻によるモデル大気を用いた 最近の結果と合致する。 |
掩蔽観測は発展途上の技術であるが、Teff 決定においては既に最も豊かな 結果を出している。複数観測の相互対照から、観測エラーが十分に小さいことが 確認されている。 |