Star Counts Redivivus I. A New Look at the Galaxy at Faint Magnitudes"

Reid,N., Majewski
1993, ApJ 409, 635 - 662



　アブストラクト

モデルと観測とのずれ　

　北銀極方向の深いスターカウントデータ(Majewski 1992) を銀河系恒星分布モデルを 用いて解析した。カラーを無視した等級分布は予想と合うが、 V > 20 でのカラー 分布に大きな差が生じた。その等級で、「標準」モデルはハロー星を超過予想、円盤星 を過小予想した。実際には V = 21 では円盤種族が多い。

暫定モデルのハロー　

　この差の原因を追究し、より合う暫定モデルを提案した。我々の見出したのは、 「標準」モデルのハロー光度関数が球状星団と全く合わないということだ。もしも、 青い星のカウントに Mv = 6.25 まで球状星団の平均光度関数を, それより下には近傍星光度関数を用いればフィットは向上する。それは、Mv = 5 付近で二つを合わせるより良い。それにハローの密度規格値を円盤の 0.15 ± 0.03 % に取り、軸比を C/a = 0.8 ± 0.05 にすると良い。 		暫定モデルの円盤　

　広がった厚い（E/T）円盤のスケール高は 1400 - 1600 pc で規格値が 2.0 - 2.5 % がよい。この円盤の色等級図が古い円盤([Fe/H] = -0.1) と 47 Tuc ([Fe/H] = -0.65) の中間だとカラー分布が良く合う。

(B-V) ∼ 1.5 で V > 19 星の密度の問題　

　カラー (B-V) ∼ 1.5 で V = 19 より暗い星のかなりを説明するには M v > 10 星の局所密度を上げるか、古い円盤内の M 型矮星スケール高を ∼ 400 pc くらいにする　（同じ事じゃないのか？） 必要がある。

　１．イントロ　

ハーシェルから HST へ　

　ウイリアム・ハーシェル 1785 が 20 フィート望遠鏡を用いて「星の寸法取り」 ( star gaging ）を試みて以来、スターカウントは銀河系構造を調べる方法として 用いられてきた。初期の研究は単純で、ハーシェルは全ての星が同じ燭台力 (candlepower) を有すると仮定していた。しかし、最近１０年間には Bahcall, Soneira 1980, 1984, Gilmore 1981, 1984 のようなモデルにと進化してきた。大規模な写真乾板 自動計測(Kron 1980) や HST の打ち上げがこの方面の研究を加速している。

「厚い円盤」　

　近年の研究の初期には、特に「厚い円盤」の存在を廻って議論 (Gilmore, Reid 1983, Bahcall 1986) が交わされた。現在では、Gilmore, Wyse, Kuijken 1989, Casertano, Ratnatunga, Bahcall 1990 に見られるように合意に達している。ただし、 個々の成分の特性に関しては未だ決定解はない。我々はモデルと観測との間に多くの 矛盾を見出している。この論文の動機はこれらの矛盾に光を当て、モデルを観測に 適合させることである。

シュミットデータ　

　最近のスターカウントへの興味の高まりに比して、実際の観測例は少ない。その上、 大部分はシュミット乾板 (Buser, Kaeser 1985, Gilmore, Reid 1983, Gilmore, Reid, Hewett 1985, Stobie, Ishida 1987) で 19 等までしか達していない。その結果 これらのデータはハローの構造を探るには適していない。

SA 57 の深い測光　

しかし最近、Majewski 1992 は Kron 1980 の SA 57 領域 0.29 deg2 乾板の再解析を終えた。多くの 乾板と CCD 測光に基づく高精度較正により、この研究では V ∼ 21 までの正確な 測光のみならず、銀河の混入を効率よく取り除くことができる。現在まで V > 21 に達したデータは本研究以外にはない。Kron 1980 は同じくらい暗い等級に達している が銀河の除去が不十分である。本データセットのみが銀河面からはるか上方の準矮星 を現場で測ることができるのである。

暫定モデルの提示　

　SA 57 データをスターカウントモデルと較べた結果、大きなズレが発見された。 この論文では暫定結果の述べ、パラメターの修正を今後の論文で行う。一箇所のみの データでは確実な結果に到達することは難しい。しかし、我々の結果はこれまで発表 されたどのモデルも SA 57 の深いデータを説明できないことを明らかにした。

　２．SA 57 領域の深い測光　


　２．１．観測　

測光　

　データの詳細は Majewski 1992 にあるのでまとめを述べる。暗い星の測光は KPNO 乾板の PDS 測定で行われた。星像は Stetson 1979 のプロファイルフィット で測定され、異なる乾板間の同じ星の測定は変換で共通システムに統一された。 共通システムでは装置等級が平均される。BJ の決定には 20 乾板が 使用され、RF の決定には 11 乾板が使われた。限界等級は BJ ∼ 21.5, RF ∼ 22.5 である。装置等級較正のために 72 星が 光電測光された。これらの参照星の等級は全域に及んでいる。測光ランダムエラーは BJ = 22 で　0.02 等以下、RF = 21 で 0.03 等以下である。

混入銀河　

　Kron 1980 の星・銀河カタログに基づき銀河を分離した。このカタログは過去１０ 年間、星、銀河、ＱＳＯのサーベイの基礎であった。そして、我々が扱う範囲では 分類は信頼できることが判っている。Kron カタログから得られるカラー分布をスター カウント解析に使用したのは Bahcall, Soneira 1980, 1984, Gilmore 1984 だけで ある。我々のカタログは Kron に較べ幾つかの点で優れている。

　まず、Kron より多くの乾板を使用し、プロファイルフィットで処理されている。 測光標準星の数も多い。また、較正が乾板がサチる BJ ∼ 19 と　 RF ∼ 18 より明るい方まで伸びている。最後に、最近の QSO 種族 の解析結果が取り込まれている。（Kron et al 1991）Kron カタログは Majewski 1992 より深いことを注意しておく。我々は彼の深いサンプル RF > 21.5 より 暗い部分はデモ用に図に入れた。


　２．２．スターカウントへの銀河混入


図．1. SA 57 領域における銀河混入。
　　　縦軸＝ log N(/0.29 deg2/mag)、横軸 = RF
　　　実線＝星。点線＝銀河。破線＝ＱＳＯ+コンパクト銀河。
　　　一点破線＝Majewski 修正(星からＱＳＯへ)の効果
　　　上は全カラー、下二つはカラー制限。青いサンプルで銀河混入が大きい。

諸天体の光度関数　

RF ∼ 20 より暗い方では銀河の混入が問題となる。図１に光度関数を 載せた。 RF > 20.5 の暗い天体では銀河が星の５倍にまで増加する。 これが暗い天体では星と銀河の分離が重要となる理由である。銀河は Kron 1980 の 銀河カウントから取った。QSO とコンパクト輝線銀河は Kron が現在進めている QSO サーベイからとった。コンパクト輝線銀河はサーベイの 25 % を占めている。

QSO + コンパクト輝線銀河 の混入　

　図１の左パネルを見ると、18 < RF < 21.5 ではこれらの系外 天体のナンバーカウント上の割合は 5 % - 10 % で小さい。
　銀河の方が多く見えるけど？　「系外天体」に銀河は 入れていない？　
しかし、暗い等級では星のカラー分布に及ぼす影響は小さいとは言えない。それは、 右パネルの BJ - RF < 1.17 （ B - V < 1.0 ）と BJ - RF < 0.7 （ B - V < 0.6 ）天体のカウウント に現れている。( QSO + コンパクト輝線銀河 ) の混入は最も青いカラーでは一番大きい。 20.5 < RF < 21.5 で見ると、B - V < 1.0 では星対( QSO + コンパクト輝線銀河 )比 = 101:23 であり、B - V < 0.6 では 39:13 である。 このように、暗く(V > 20.5)青い(B - V < 0.6) 星状天体の少なくとも 25 % は 銀極方向では系外天体なのである。

QSO の同定　

　Kron et al 1991 カタログはこの等級で最も完璧な QSO サーベイであるが、 実際の QSO 混入はより大きいかも知れない。第１に、ここまでは、分光で確認さ れた QSO とコンパクト輝線銀河だけを扱ってきた。しかし、 RF ≥ 21 ではかなりの数の候補天体が確認に十分なスペクトルを欠き、未だに星カタログ に載っている。第２に SA 57 の最近の研究（Majewski et al 1991, Trevese et al 1993）によると、変光を示すが固有運動が検出されない星状天体が UBV



カラーが恒星と同じため以前には発見されなかった QSO と判った。我々の 星カタログに載っているこれらの QSO 候補天体が確認を待っている。図１には、 一点鎖線で QSO + コンパクト輝線銀河 と星のカウントの双方が、もしこれらの 追加 QSO 候補が真の系外天体であったら、どう影響されるかを示している。 測光が信頼できる最も暗い区間 20.5 < RF < 21.5 では、星と QSO + コンパクト輝線銀河 の比が、B-V ≤ 1.0 で 91:33, 、B-V ≤ 0.6 で 35:17 まで下がるかも知れない。

系外天体除去が不十分だと　

　要するに、銀河系を V > 20 の暗いところで調べるなら、星/銀河/QSO の正確 な分離の重要性は強調し過ぎることは無い。二つの重大な効果は
（１）星の見かけ面密度は減少するため、V = 20 までには星の数は銀河の数に
　　　圧倒されてしまう。
（２） QSO + コンパクト輝線銀河 の見かけ面密度は増加するので、その割合が
　　　正確に評価されないと、青い星の見かけ数を 30 - 50 % 増加させる。
これらの系外天体の除去がきちんとなされないと、遠方ハローの密度を過大に見積もる、

　３．モデル　


　３．１．モデルの構造　

新しい表示法　

　スターカウントモデルは次に示す Seeliger 1898 式に基づいている。

　A(m, S) = ΣAi(m, S) = ΩΣ∫Φi (M, S) Di(r) r2 dr

ここに、A(m, S) はスペクトル型（またはカラー）が S で見かけ等級が m の星全ての 数、Φi(M, S) は i-種族の光度関数、 Di(r) は密度則 である。
　これまでのモデルは n (b, l, m, カラー）を表で与えていた。本論文では、 n (b, l, r, M, カラー, 速度）の表 (Reid 1992) を作る。こちらの方がより柔軟な扱い が可能だからである。

副種族の色等級図　

　我々の方法は副種族毎に色等級図を選ぶことから始まる。CMD に沿って区切り点を 打っていき、その区間内の星密度 (星 pc-3) を決める（光度関数）。 この方法は非均一な等級区間分けを可能にする。この方法で準巨星、レッドクランプ、 水平枝などの特徴を考慮に入れやすくなる。さらに、異なる副種族の系列を組み合 わせて種族内の年齢分布、組成変化を表現することが出来る。

モデルの構築　

この先の内容が判らない。逐語訳を載せる。
　次に、円錐形の標本領域を距離で区分し、区間内の星の数 n または絶対等級 Mv+ΔMv を採用した密度則に従って求める。 各星には ΔMv の範囲内で出鱈目に選んだ等級が付けられる。 この等級範囲はカラーでは ±Δ(B-V) または ±Δ(V-I) に対応する。カラーはその等級 Mv に釣り合った値を付ける。もし、 その星に付ける等級を

　　　　　 Mv' = ⟨ Mv ⟩ + 0.3 ΔM v

とするなら、

　　　　　(V-I)' = ⟨ (V-I) ⟩ + 0.3 Δ(V-I)

である。それに距離 r もつける。星間吸収は無視する。距離は r3 で 一様になるよう分布させる。最後に、観測された等級とカラーは、色―等級関係の コスミック分散と観測不定性を許容するようにガウス分布の摂動をかけられる。この モデルを Bahcall, Soneira モデルと Gilmore 1984 モデルで試し、彼らの結果を 再現することが出来た。

　３．２．円盤成分　


　３．２．１．古い円盤　

暗い端での光度関数の形　

　近傍星の大部分は高速で回転する円盤種族の一員である。それらの光度関数は Wielen, Jahreiss, Kruger 1983 により Mv ∼ +13 まで良く決 められている。その下になると、近傍星は平坦な光度関数を示唆するが、深い 測光（Reid, Gilmore 1992, Tinney, Mould, Reid 1992）は Mv = 12.5 でピークに達していることを示す。後者に含まれる連星がその差の原因と いう意見もある。しかし、Reid 1991 は連星の影響は無視できる程度であると 主張している。ただ、V = 21 より暗くならないとこの問題の影響は効いてこない。

近傍星の色・等級関係　

　近傍星は円盤の色-等級関係を与える。Bessell 1990 は Gliese 1969 カタログ から選んだ 900 星の BVRI 観測を行った。一方、Leggett 1992 は彼女の集めた データにJHKL 赤外データを加えた。我々はBessell の色-等級関係を使用したが、 Leggett との差は非常に赤い星の部分だけである。そこに含まれない巨星枝に 対しては NGC 188 (McClure, Twarog 1977) を使った。ただし、巨星枝は V ∼ 14 より暗い所では無視できる効果しかない。


スケール高　

　銀河面に垂直方向の速度分散 σz は年齢と共に増加して行く。 Wielen 1974. スターカウントモデル Bahcall, Soneira 1984, Gilmore 1984, Yoshii, Ishida, Stobie 1987, Robin, Creze 1986 はスケール高を、Mv &le: +2 に対する 100 pc から Mv >: +4 に対する 350 pc へと変化する 指数関数型密度則の採用でこれに応じてきた。これらの観測的基礎は Reid, Gilmore 1983 に与えられている。 Mv >: +10 の星に対してはスケール高の観測 はない。最近 Kuijken, Gilmore 1989 は K 型矮星に対し 249 pc という小さな値を 与えた。距離は測光視差[Mv, B-V]で与えられた。彼らは広がった/厚い円 盤のスケール高にも 1000pc という小さな値を得ている。しかし、これらは小さすぎる ことを後に示す。


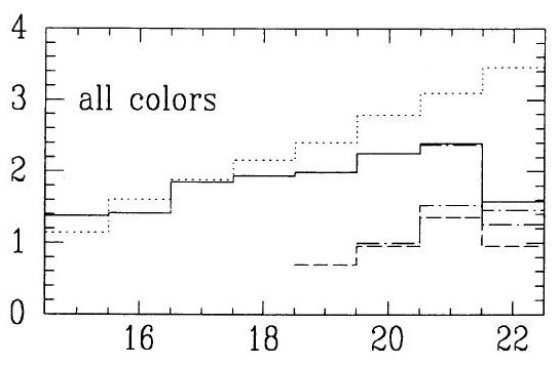
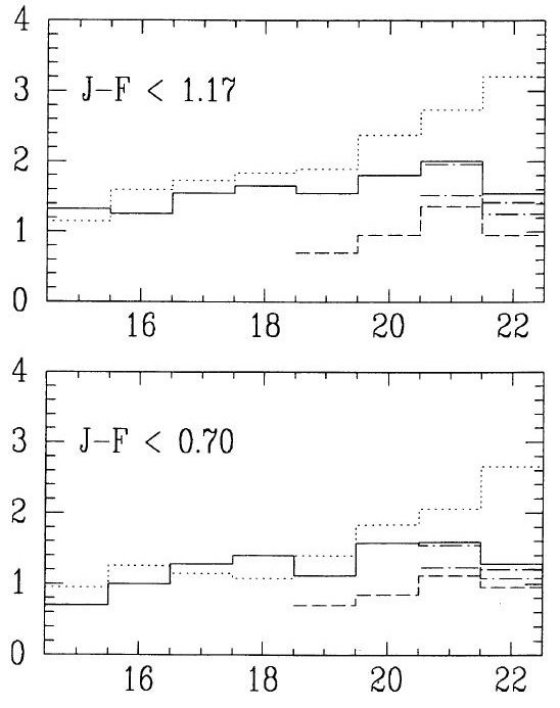
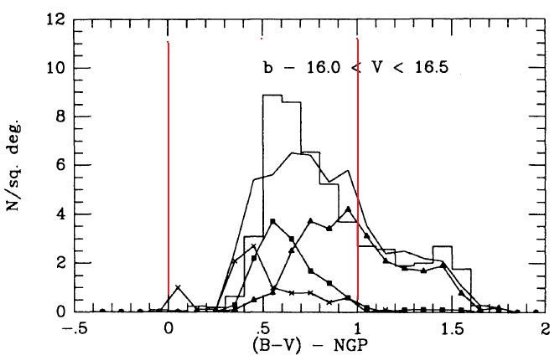
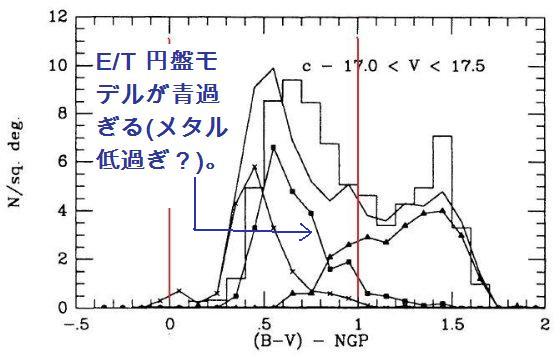
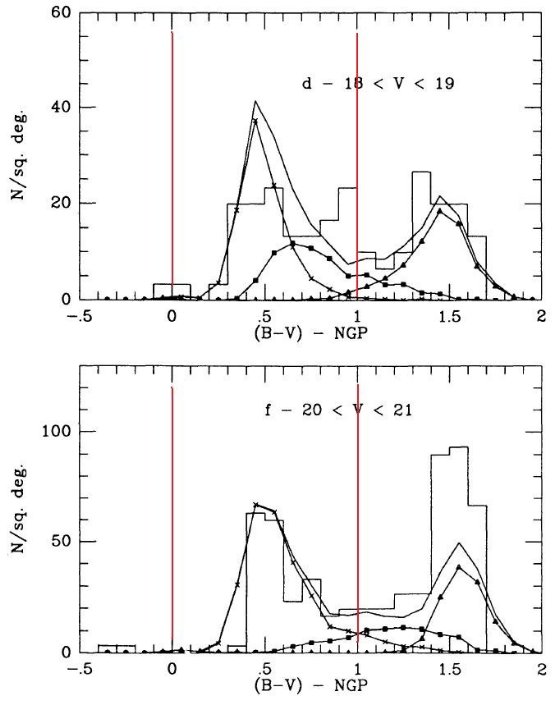
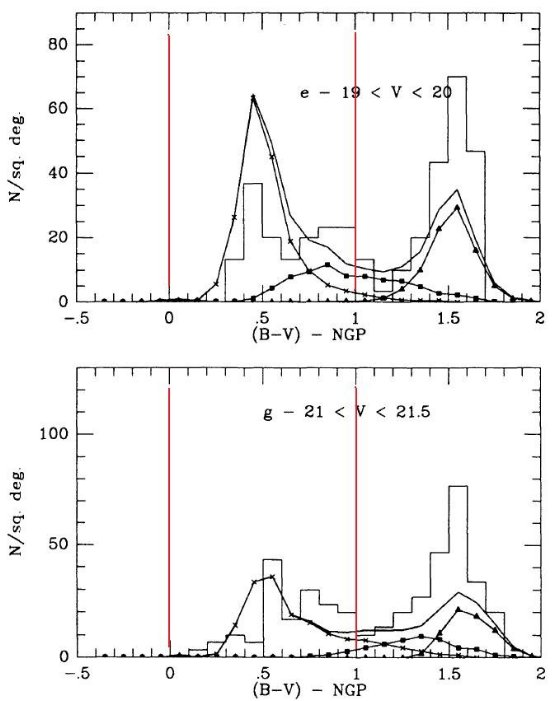
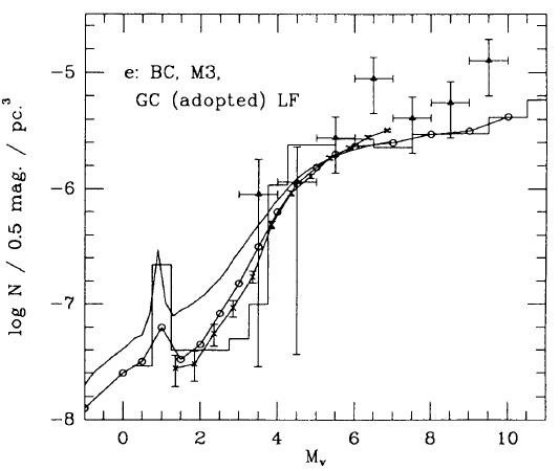
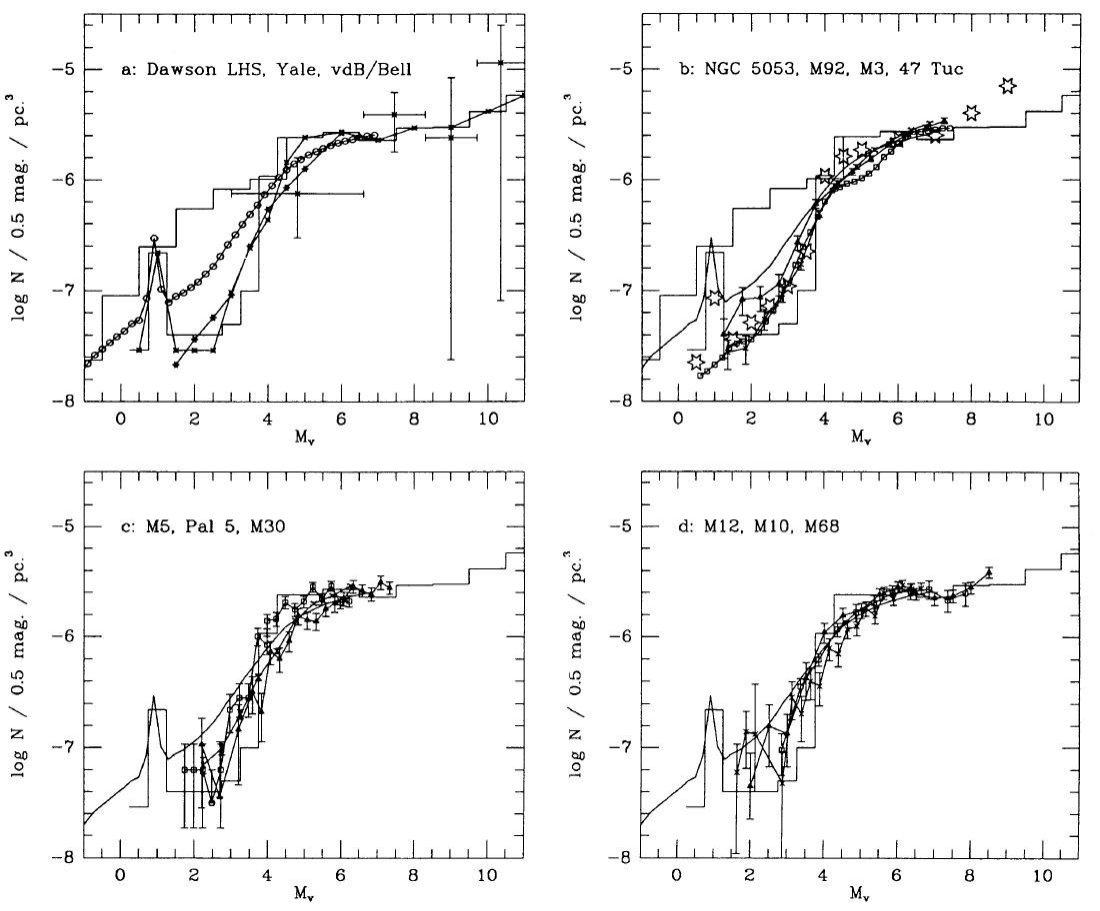
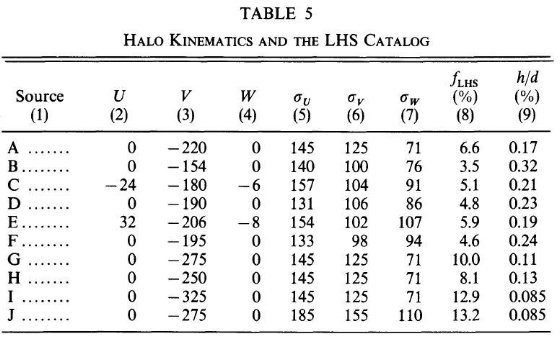
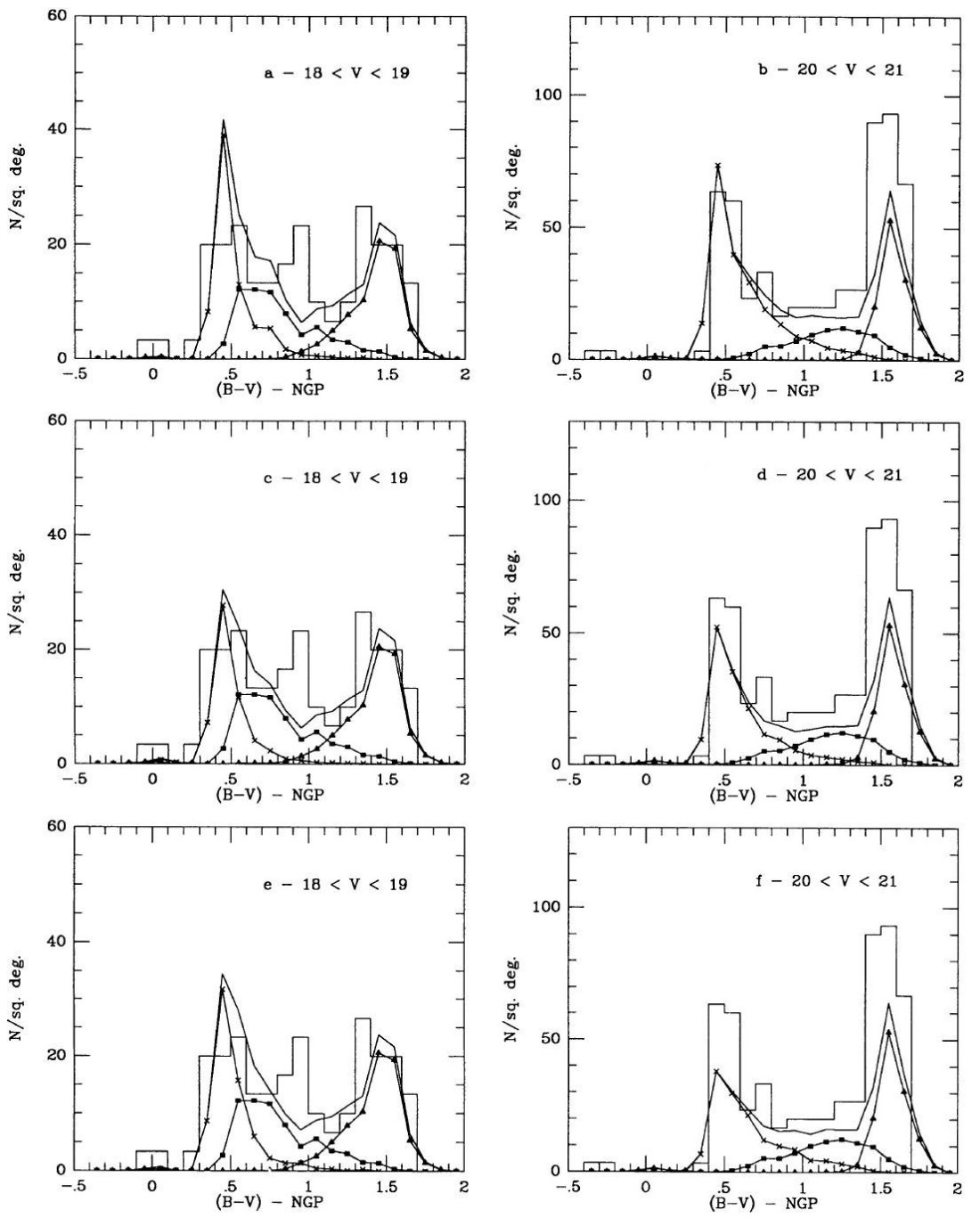
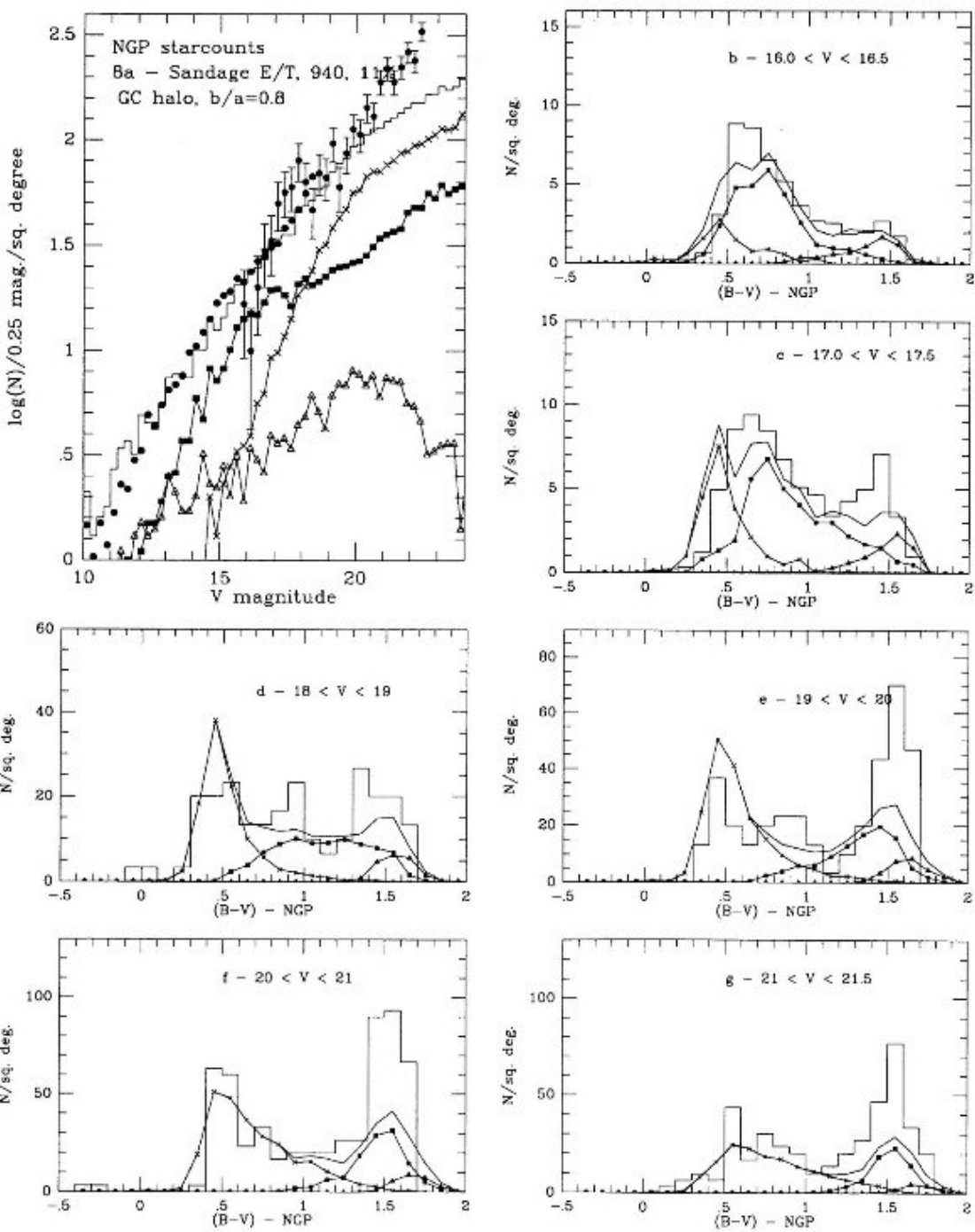
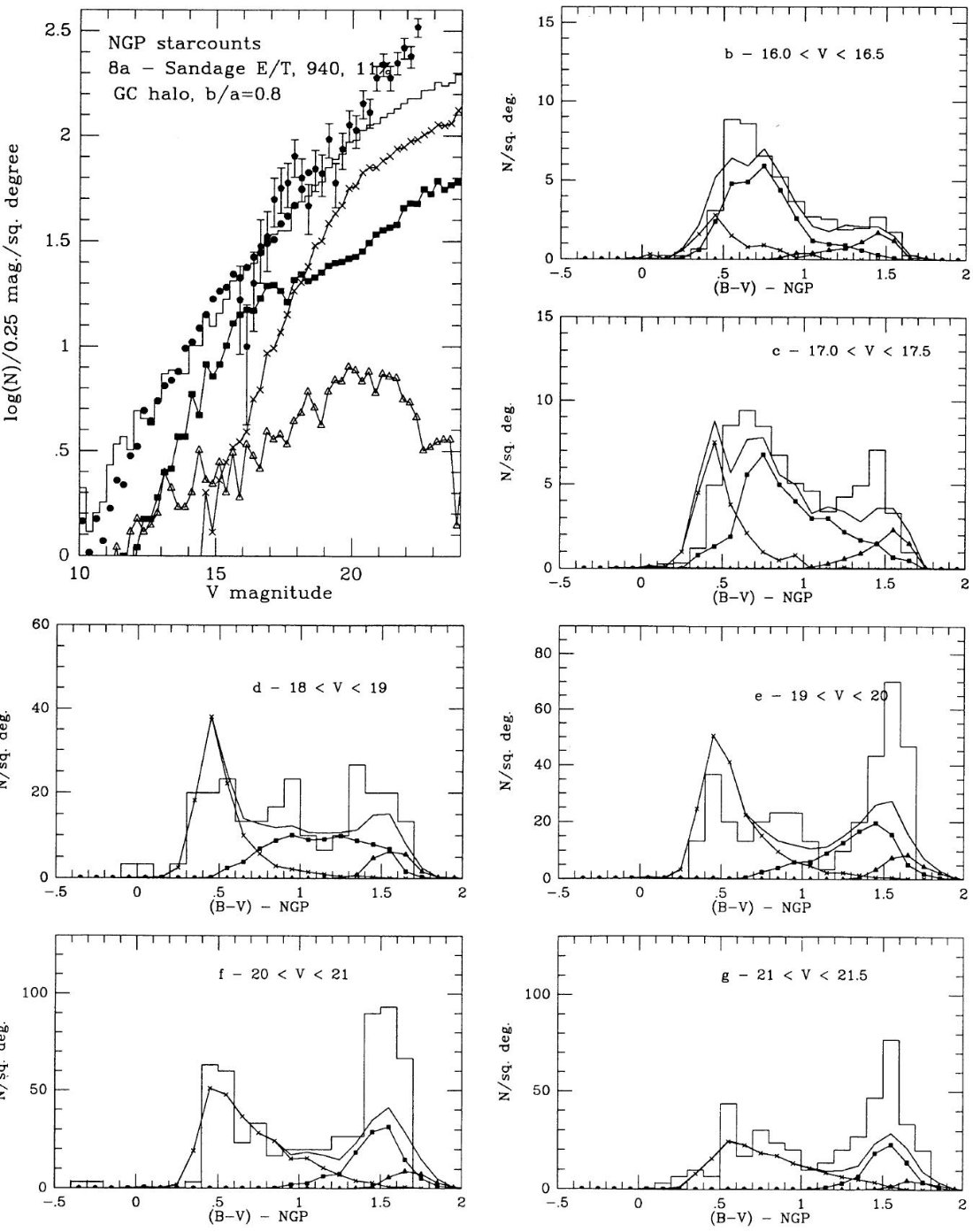
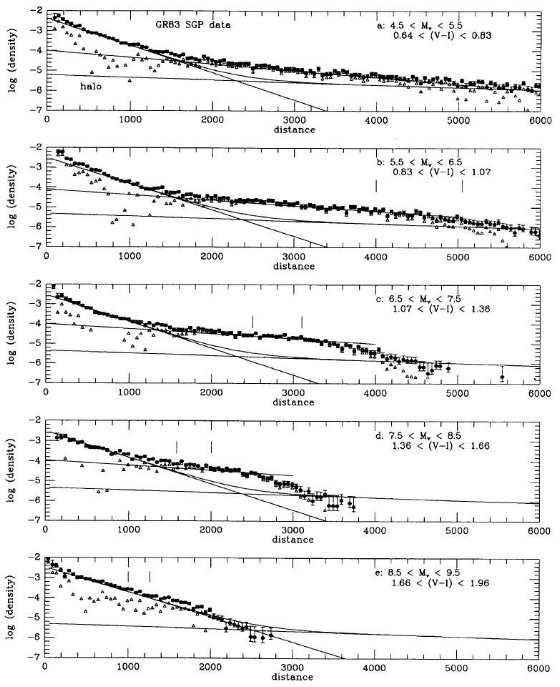
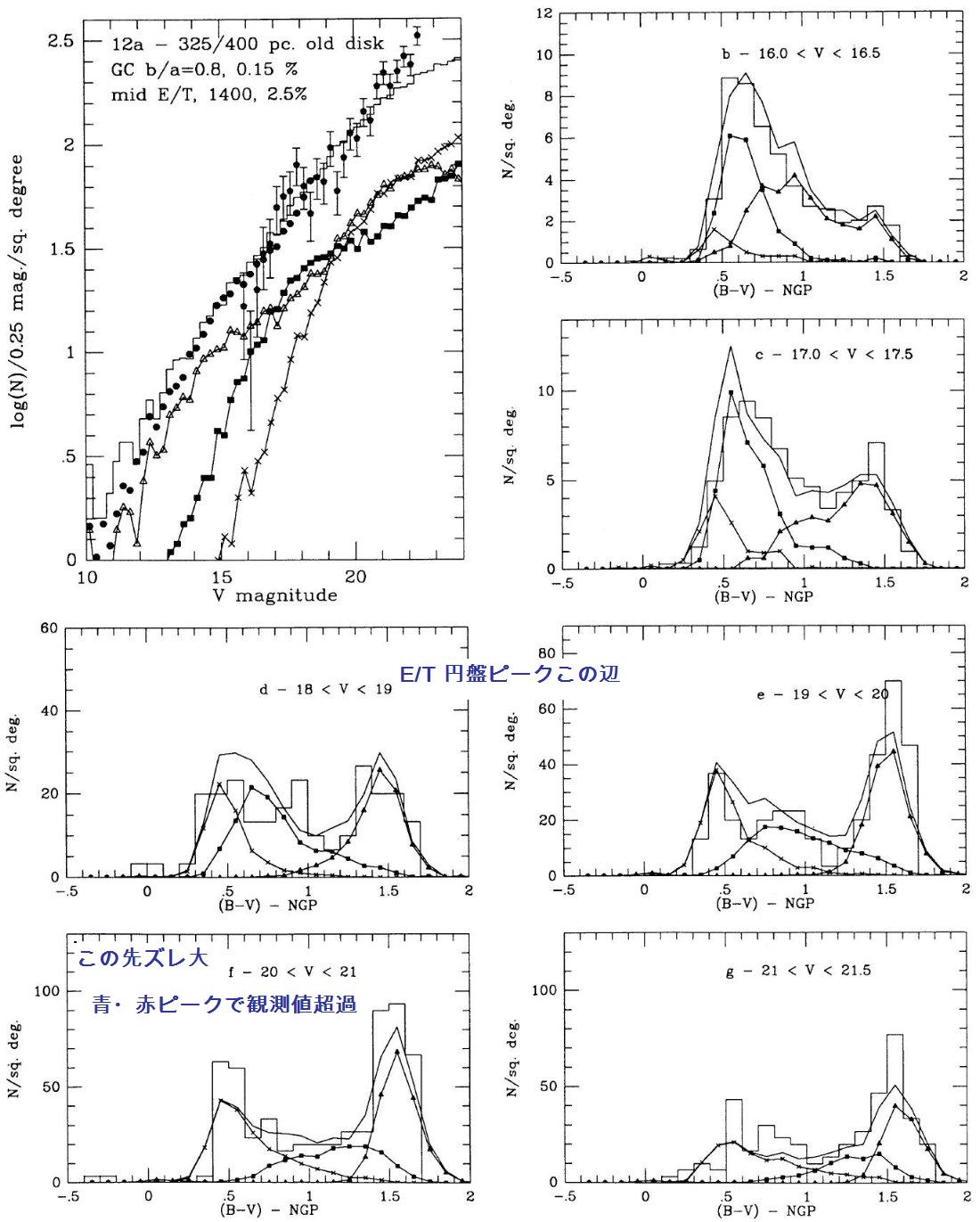
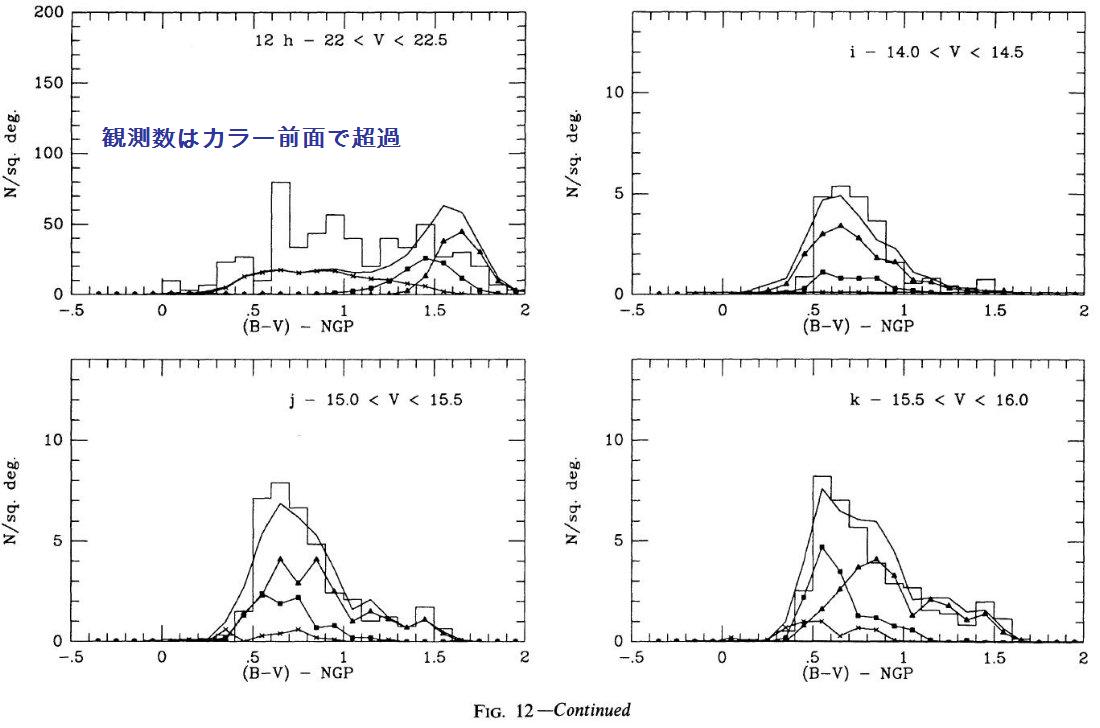
　３．２．２．広がった/厚い（E/T）円盤　

銀河面に垂直方向の密度分布　

　銀河面に垂直方向の密度分布、Elvius 1965, Becker, Fenkart 1976, は勾配 が高度 1 - 2 kpc で変化することは以前から知られていた。Gilmore, Reid 1983 はこの事実を、スケール高 325 pc の薄い円盤の上に別の恒星種族が広がっている と解釈した。彼らはそれを 1958 年バチカン会議で定義された 中間種族 II に 関連すると考え、厚い円盤と名付けた。中間種族 II と関係があるとした最大の 理由は厚い円盤のスケール高が 1450 pc であり、速度分散 σz ∼ 60 km/s を示唆していたからである。この値は近傍 RR Lyr 星, Woolley 1978, Strugnell, Reid, Murray 1987, のそれと近い。この星は太陽に対し回転遅れ ∼ 100 km/s を有し、高速で回転する古い円盤と異なる起源を持つことを予想させる。

光度関数の明るい端　

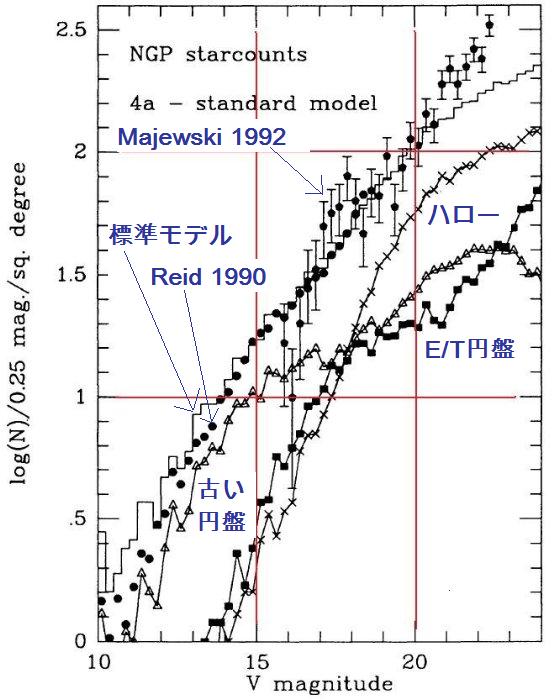
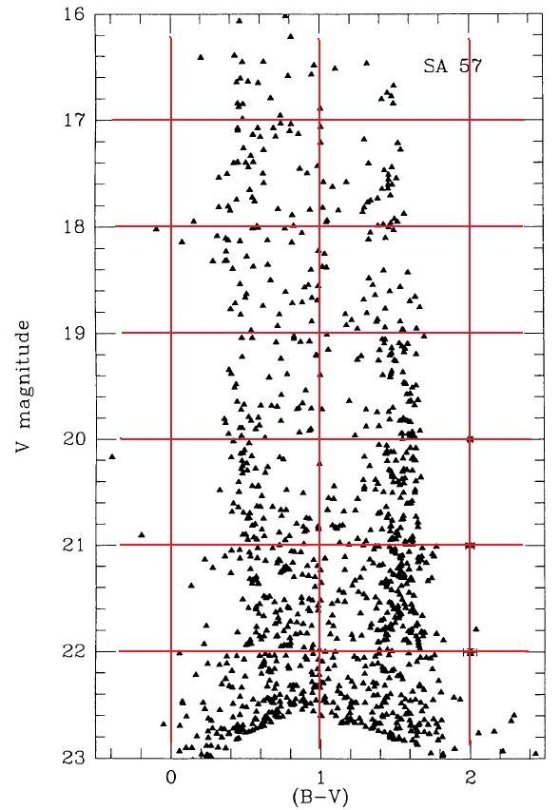
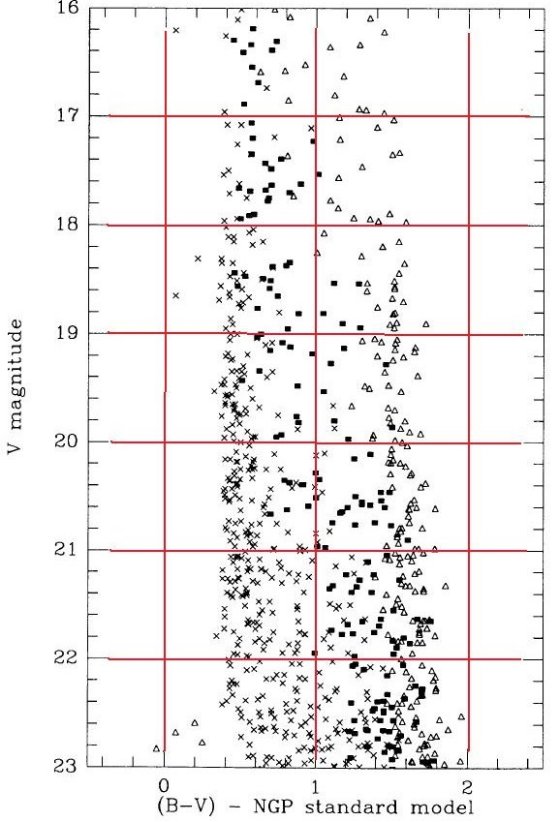
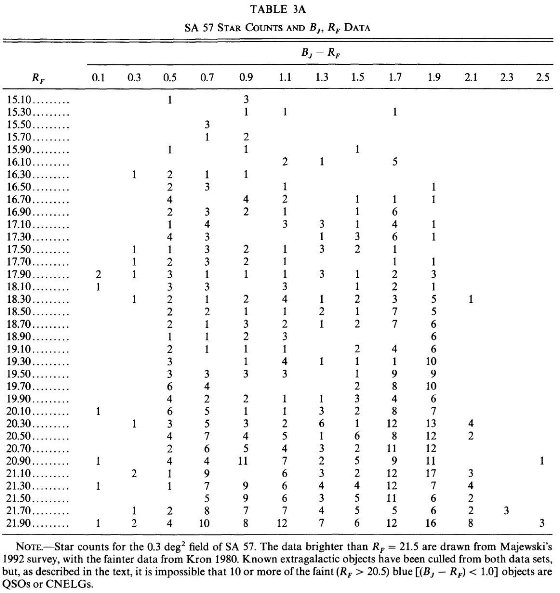
　Gilmore, Reid 1983 はまた、銀河面から上がっていくに連れ光度関数の明るい端 の勾配が急になっていくことに注目し、それを厚い円盤は古い(数 Gyr)種族であると 考えた。彼らは厚い円盤の規格値を 2 % と見積もった。Gilmore et al 1985 は l = 37°, b = -51° での　V = 19 までのスターカウントは上のパラメター と合うことを示した。

厚い円盤は独立の種族か？　

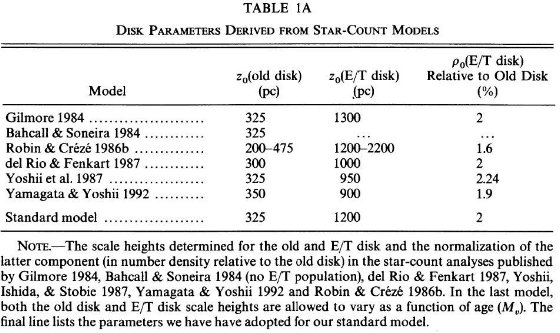
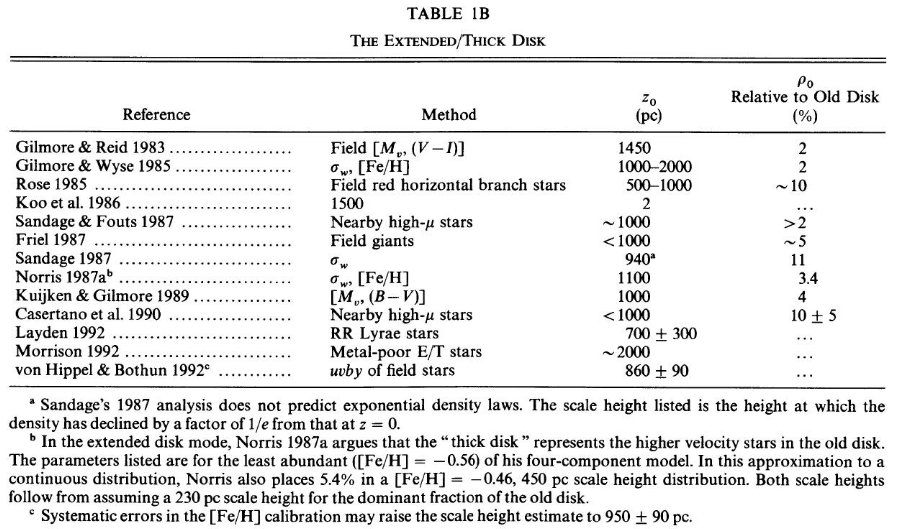
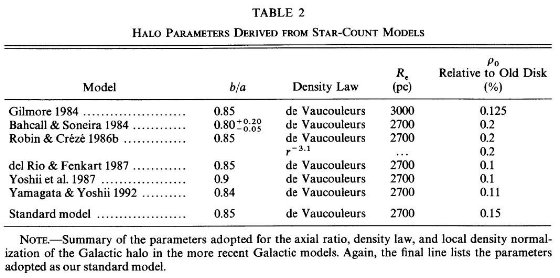
　厚い円盤が独立の種族か、Gilmore, Wyse 1985, Gilmore et al 1989, Carney, Latham, Laird 1989, 単に古い円盤の速度分散高速テールに過ぎない, Norris 1987, Norris, Green 1989, Norris, Ryan 1991, かの議論は今も続いている。表１A には スターカウント全体をフィットする解析で厚い円盤を表に出した銀河系モデルのパラ メターを載せた。一方、表 1B には特定の星をトレーサーに使用して厚い円盤を 調べた研究を集めた。Gilmore, Wyse 1985, Sandage, Fouts 1987, Sandage 1987, Casertano et al 1990 は速度に基づいて厚い円盤種族と看做せる星のサンプルを 解析した。Friel 1987, Morrison, Flynn, Freeman 1990 は巨星を使った。Rose 1985 は赤い水平枝星を使ったが、Norris 1987, Norris, Green 1989 はそれらは 古い円盤のレッドクランプ星ではないかと疑っている。Layden 1992 は高メタル RR Lyr 星を用いた。表 1B には普通のフィールド星に対する測光視差の解析結果、 Gilmore, Reid 1983, Koo, Kron, Cudworth 1986, Kuijken, Gilmore 1989, Hippel, Bothun 1992 も含めた。ただし、スターカウントモデルで色等級図からそれらの 結果が予言できるかどうかのテストは行われていない。その点で無矛盾性は確立し ているとは言えない。特に最近のスケール高は小さい。

厚い円盤のスケール高　

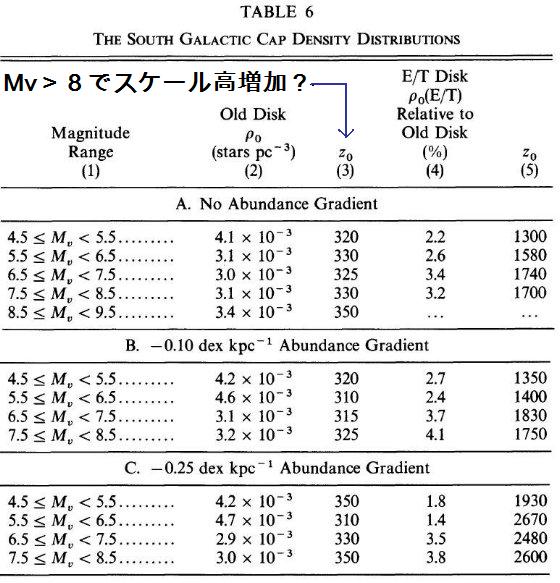
　広く見て、表１b のスケール高は当初の Gilmore, Reid 1983 より小さく、規格値は 大きい。我々は 3.5 kpc という等しいスケール長を古い円盤と厚い円盤の双方に適用 した。しかし、銀極データのみを扱っているのでこの値自体は結果に影響しない。

厚い円盤のスケール高　

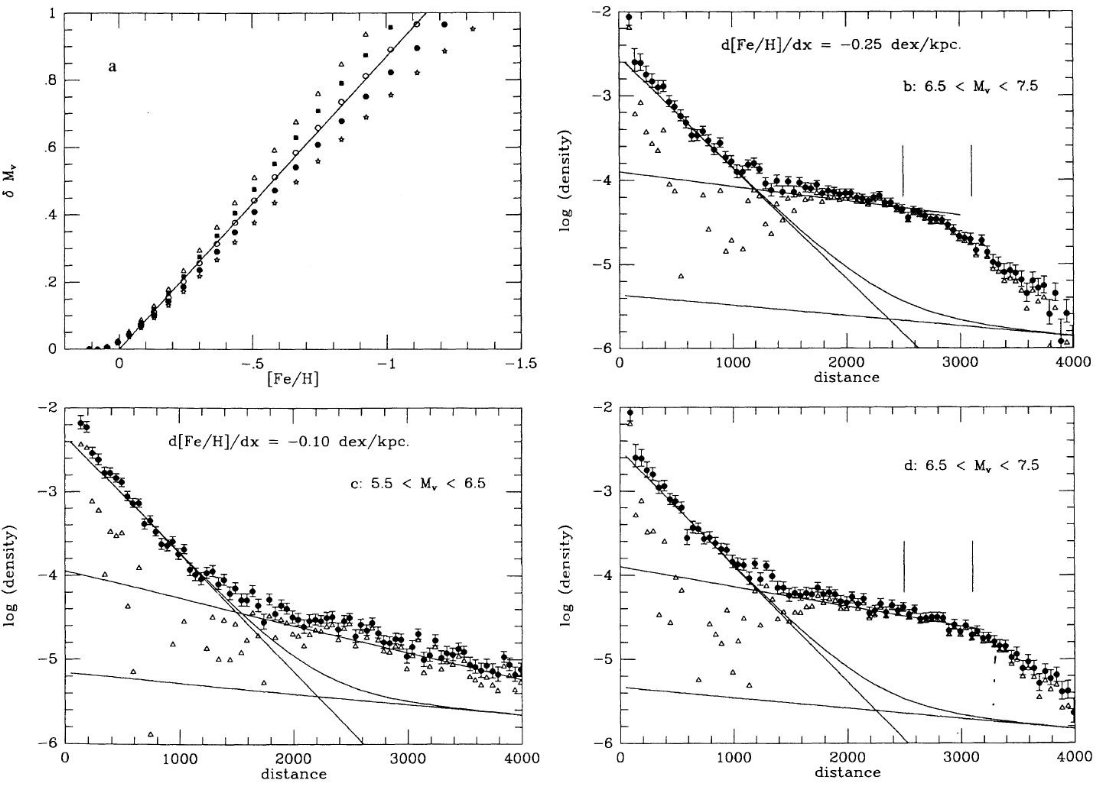
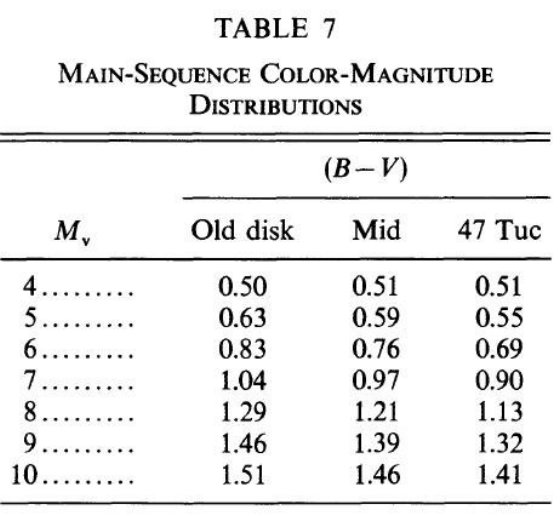
　Morrison et al 1990 の観測は 厚い円盤のメタル量分布が [Fe/H] ∼ -1.5 まで 達し、平均は [Fe/H] ∼ -0.6 であることを示した。(Gilmore et al 1989, Carney et al 1989) そのうえ、それらの星は高メタル厚い円盤球状星団と関係すると された Zinn 1985, Armandroff 1989. これらの結果及び Rose, Agostino 1991, Friel 1988 の研究を考慮して、高メタル([Fe/H] ∼ -0.65)球状星団 47 Tuc を我々の 標準モデルにおける厚い円盤の色等級図に採用した。47 Tuc の B-V カラーは Hesser et al 1987 の観測から、R, I データは VandenBerg, Bell 1985 モデルから決めた。
ちょっと変則的な決め方である。
この星団は、厚い円盤のメタル量として定めた [Fe/H] = -0.6 より僅かに 低メタル [Fe/H] = -0.65 である。しかし、 VandenBerg, Bell 1985 モデルによると、 (B-V) で　0.02 のズレがターンオフで [Fe/H] = -0.5 に合わせるのに必要である ここのところ意味不明。 Carney et al 1989 		RR Lyr と 47 Tuc　

　47 Tuc を厚い円盤の標準に選ぶことには議論があるかも知れない。厚い円盤の トレーサーとしてよく用いられる RR Lyr は 47 Tuc に少ないことで有名であるから。 ここで指摘しておきたいのは、これらのモデル（？）は最終的なものではなく、ハロー の水平枝を研究することは目的にしていないという点である。47 Tuc が選ばれたのは その主系列が他の高メタル球状星団より詳細に調べられていたからであり、RR Lyr を 持つ他の高メタル球状星団 M 71, NGC 6171 は赤化がそれぞれ 0.31 Arp, Hartwick 1971, 0.38 Da Costa, Mould, Ortolani 1984 と 47 Tuc の 0.04 に較べて大きいため 不適当であるからである。さらに最近の研究では、厚い円盤の運動学は高メタル RR Lyr とそれほど一致せず、それらが厚い円盤の代表であるかどうか怪しくなっている。

厚い円盤という名称（１）　

　厚い円盤の特徴は Gilmore,Reid 1983 で余りの星が出たのと高メタル RR Lyr 星 から来た。厚い円盤のスケール高 1500 pc から Gilmore, Reod 1983 はその速度分散 を σz ∼ 60 km/s と見積もり、RR Lyr 星の運動から厚い円盤 の回転遅れを ∼ 100 km/s とした。( Strugnell et al 1987). その後の観測から 太陽に対する回転遅れは ∼ 35 - 40 km/s (Dawson 1986, Morrison et al 1990, Casertano rt al 1990) と変わった。しかし、Murray 1986, Spaenhaver 1989, Majewski 1992 はその非対称ドリフトが高度と共に増加することを見出している。 その間「厚い円盤」は円盤やハローと異なる独立の恒星集団であると看做されて きた Carney et al 1989, Wyse, Gilmore 1989. 特に Carney et al は固有運動から 選んだ厚い円盤星のメタル量分布が古い円盤と異なり、別の種族であることを示唆 すると主張している。

厚い円盤という名称（２）　

　一方、Norris 1986, 1987a,b は銀河面から垂直な方向での複雑な密度分布は、 円盤には異なる速度分散と従って異なる垂直密度則を持つ異なる年齢の星が含まれ ていることを反映している、と主張している。Norris 1987a の４成分モデルの中 で最も速度分散が大きいグループは σw = 33 km/s で、銀河面の 上方離れた所で観測された 40 km/s より少し小さい。注意するのは、Wielen, Fuchs 1983 によると、銀河系円盤の歴史の間に十分な量の降着があれば 40 - 50 km/s の 速度分散が達成される。いずれにせよ、大きなスケール高を持つ「広がった円盤」は 円盤の最も古い星を含み、それらは銀河面から最も大きな散乱を受けているのである。 Norrius, Ryan 1991 は、固有運動で選ばれたサンプルのメタル分布を 説明するには、このモデルの方が良いと主張している。

厚い円盤という名称（３）　

「厚い円盤」も「広がった円盤」のどちらの術語も好ましくない特定の形成モデル との結びつきを産み出してしまう。これはバチカン会議で使われた「中間種族II」 と似ている。我々は、可能性のある起源説に関係なくデータを処理したい、つまり 円盤ができてからの期間の間巨大な天体による継続的散乱によるのか、円盤の歴史の 初期に合体した天体に対する力学的反応なのか、に無関係に。そこで、中間の柵の 上にまたがる命名 「E/T 円盤」という名前を採用する。


表１a．厚い円盤を使った解析と使わなかったスターカウント解析の例


　　　　　　　　　　　　　　　　表１b．厚い円盤のパラメター

　３．２．３．「標準」モデルのパラメター　

５つのスターカウントモデル　

　ここで標準モデルを作る目的は、SA 57 の深いデータに最近の銀河系モデルが どの程度耐えられるかを試す事にある。表 1A は最近のスターカウントモデルで 使われた古い円盤と E/T 円盤のパラメターである。一番下に波我々がそれらの 平均として適当と思った値を載せた。表 1A ( 1B と間違 えている) の５つのモデルはスターカウント解析から導かれた最新結果 であり、つまり自己無矛盾な銀河系全体のモデルであって、特定の個別天体に 付随するパラメターではない。

Robin, Creze 1986a,b の連続モデル　

　５つの中で Robin, Creze 1986a,b が最も複雑である。彼らは薄い円盤と E/T 円盤(彼らの用語では中間種族II)の双方で年齢と共に上昇するスケール高を採用 している。したがって、年齢 3 Gyr の円盤星（σw ∼ 20.5 km/s ）はスケール高 z0 ∼ 360 pc で、 5 Gyr（σw ∼ 25 km/s ）は z0 ∼ 475 pc となる。同様に、 中間種族II はスケール高 1180 (12 Gyr) から 2210 pc (14 Gyr) まで分布する。 我々も似た方法を採用するが副種族の数はもっと少ない。

「標準」モデルパラメター　

　我々の（表1A 最後の列）「標準」モデルパラメターは以前の結果の平均を取って いる。薄い円盤に対しては３つの副種族、
　　　若い円盤：　　　　　年齢 ∼ 3 × 108 yr, スケール高 100 pc,
　　　　　　　　　　　　　　　　ヒアデス的 CMD (Upgren, Weis, Hanson 1985)
　　　中間年齢円盤：　　年齢 ∼ 2 Gyr, スケール高 250 pc, 近傍星 CMD
　　　古い円盤：　　　　　スケール高 325 pc, 近傍星 CMD (Bessell 1990)
一方、E/T 円盤：　　　　スケール高 1200 pc, 47 Tuc CMD

を採用した。これらから作り出される「星」には V 等級不定性として σ ∼ ± 0.05 mag, カラーには σ ∼ ± 0.08 mag のガウス型エラー を加える。


太陽の浮き加減　

　太陽は銀河面より少し浮いている。Blaauw 1960 は若い星から約 30 pc のズレを、 Magnani, Blitz, Mundy 1985 は分子雲から似た値を、Toller 1981 はパイオニア 10 データから 12 ± 2 pc を得た。Djorgovskii, Sosin 1989 は IRAS データ から 15 - 22 pc, 山縣、吉井 1992 は北銀極と南銀極スターカウントから 40 pc を得た。我々は 30 pc を採用する。

円盤副種族の光度関数　

　各副種族の光度関数は Wielen et al 1983 による Mv < +11 近 傍星の結果にそれより暗い星に対する測光視差に基づく追加 Reid 1987 を加えて 得た。そして、Miller, Scalo 1979 による主系列寿命を用い、円盤寿命を 10 Gyr と仮定して、星を副種族に配分した。こうして Mv < +2 の全ての 星、 Mv = +2 の 30 %, Mv = +3 の 20 %, Mv = +4 の 10 %, Mv ≥ +5 の 3 % は若い円盤に付けられた。そして、 +2 ≤ Mv ≤ +3 残りの星、 Mv = +4 の 45 %, Mv ≥ +5 の 17 % は中間年齢円盤に付けられた。Mv = +4 の 10 %, Mv ≥ +5 の 80 % は古い円盤に付けられた。 極方向スターカウントは若い円盤も中間円盤もスターカウントに寄与しない。


「標準」円盤での E/T 円盤　

　「標準」円盤での E/T 円盤は古い円盤と同じ光度関数を持ち、規格値＝ 2 % で あると仮定する。

　３．３．ハロー的成分　

　３．３．１．以前のハロー研究　

ハロー星サンプル　

　スタ−カウント以外では、近傍の高速度星、低メタル星もように 運動学的性質から推測するものや、RR Lyr、 K 型巨星のような遠方の明るい星 を代表標本として直接そこでの密度分布を決める方法などを用いて、ハローの 構造は研究されてきた。初めの近傍星を用いる方法では、高速度星の多くは準矮星 である。そこで、ハロー対円盤星の比は準矮星のカタログに基づいて決められること になった。初期の Schmidt 1975 の研究では V/Vmax 法を横速度 Vt > 250 km/s の　17 星に適用して、太陽近傍でのハロー対円盤 星の質量比を0.125 %, 数の比としては 0.25 % を得た。この値はハローに付加する 運動学的性質に依存する。その後の研究、Richstone, Graham 1981, Dawson 1986, Bahcall, Casertano 1986 はモンテカルロシミュレーションで付随する選択効果を 評価しながら固有運動データを解析している。彼らの結果では数密度の規格値は 0.15 - 0.35 % で、値の開きは主に仮定したハローの運動学による。この点は 4.1．節で詳しく述べる。現在のところ、近傍 RR Lyr (Suntzeff, Kinman, Kraft 1991, フィールド水平分枝星 Preston, Shectman, Beers 1991) は低い方の値 を支持していることを指摘しておく。

ハロー光度関数　

　近傍星の固有運動もハローの光度関数を求めるのに使われた。Schmidt 1975, Bahcall, Casertano 1986 のどちらも準矮星の光度関数は古い円盤種族の光度 関数と矛盾しないという結論に達した。Richer, Fahlman 1992 はハロー光度関数 は円盤と違い Mv ∼ +12 を越えても上昇していくという結果を 得ている。しかしそれらは V = 22 までのスターカウントには影響しない。 ハローが古い種族でターンオフが Mv ∼ +4 に相当することを考慮 して、スターカウントモデルでは明るい進化したん星の部分に球状星団を、 主系列には円盤星の光度関数を用いた。つなぎは +4 ≤ Mv ≤ +4.5 の部分で行われた. Gilmore 1984, Bahcall 1986.

ハロー星と球状星団　

　ハローは低メタルなのでスターカウントモデルには適切な色等級図を使う必要 がある。近傍の固有運動星から, Carney et al 1990b, Ryan, Norris 1991, メタ ル分布は球状星団と似ていることが判っており、その中間メタル量は [Fe/H] ∼ -1.6 で低い方には -4 まで小さなテールが伸びている。 RR Lyr 星は 太陽円周の外側でメタル量勾配の証拠を示さない。その平均値は ⟨[Fe/H] ⟩ = -1.65 ± 0.3 である　Suntzeff et al 1991。Majewski 1992 は SA 57 距離 5 kpc 以遠の星の平均メタル量として [Fe/H] = -1.43 を導いた。 Kraft et al 1992 は M3 巨星とフィールドハローの巨星が、特に O, Na, CN 量に関し、驚くほどの類似を示すことを見出した。M3 巨星の平均メタル量は -1.47 ±0.01 でハローフィールド星のそれと近い。以前 Suntzeff 1981 や Zinn, West 1984 は [Fe/H] = -1.6 としていた。最後に Kraft 1989 は、深い サーベイ（Reid, Gilmore 1982, Hartwick 1983）による青い水平枝星と赤い水平枝 星の比は M3 や M5 のそれと合うことを指摘している。

もっと青い？　

　他の研究ではもっと青い水平枝の方がハローの典型例になるとしている。Preston et al 1991, Green, Morrison 1992 は局所的な（？）水平枝は青いことを見出した。 Preston et al 1991 によると, 青い水平枝星と RR Lyr 星の比が 6.5:1 である。 一方、Kinman 1992 は彼が観測したフィールドではその比が 1:1 であるとしている。
　強調しておきたいのは、この問題はハローの起源と形成には重要であるが、スター カウント V > 17 の解析には影響がないことである。中間メタル量の球状星団 M3, M5, M13 のどれでも我々の目的には合うので、ここでは M3 を用いる。


ハローの密度勾配　

　ハローの密度分布は、球状星団、 RR Lyr 星、青い水平枝星を用いて得られてきた。 Harris 1976, Zinn 1985 は、低メタル球状星団は r-3.5 べき乗則に 従うことを示した。[Fe/H] < -1 の（？）高メタル星団はより銀河面に追随して いる。Armandroff 1989. 星団にその質量の重みをつけて分布を決め直すと より緩い r-3, Carney et al 1990a, Suntzeff et al 1991 となる。
　RR Lyr 星はハローのトレーサーとして使えるが、メタル量勾配により選択効果が 生じる。低メタルになると水平枝星が不安定帯より青くなるからである。その上 低メタル RR Lyr 星は小振幅、長周期となり（Preston 1957）検出困難となる。 しかし、Santzeff et al 1991 の言うようにメタル勾配が強くないなら RR Lyr は 素晴らしい密度トレーサーとなる。その密度勾配はやや緩い。Saha 1985 は 5 kpc < r < 25 kpc で r-3 にフィットすることを見出したが、 Hawkins 1984 は r-3.1 とした。Kinman 1992 は RR Lyr とフィールド 水平枝星を合わせて、 r-3.5 を導いた。

ハローの軸比 c/a 　

　ハロー密度分布は密度則と全体の平坦度 (c/a) の二つで定義される。もし、低 メタル球状星団を指標にすれば、ハローの形はほぼ球形となる。しかし、10 5Mo の天体を形成する条件は普通のハロー星形成とは異なっていた可能性が ある。また、内側の星団は銀河系の歴史を通じて壊されたり影響を受けてきたかも 知れない。これらの理由で球状星団をフィールドハロー星のトレーサーに使うには 注意が必要である。それにも拘らず、初期のスターカウント（Gilmore 1984, Bahcall, Soneira 1984）が与えた軸比 c/a = 0.8 - 0.9 は Oort, Plaut 1975 が RR Lyr から得た値に近い。山縣、吉井 1992 は Kron 1980 の SA 68, SA 57 のスターカウ ントデータの解析から c/a = 0.84 という値を得た。

軸比への理論的な制限　

　初期の力学的研究は、White 1985, Levison, Richstone 1986、この軸比は近傍の RR Lyr や 準矮星が示す強く非等方な速度分散と両立しないと考えた。これらの 速度分散はもっと平坦な形を要求しているように見えた。最近の研究、 Arnold 1990, van der Marel 1991、は理論的な結論はそれほどはっきりしていなくて、 近傍の3軸不等速度楕円が強い平坦度 c/a < 0.5 を意味するわけではないことを 示した。

観測の示すハロー平坦度　

　一方では、少なくともハローのある成分が著しく平坦であることを示す証拠が ある。Wyse, Gilmore 1989 は異なる銀緯の2領域で青い星を較べ、c/a ∼ 0.6 の方が ∼ 0.8 よりよく合うことを示した。また、Wesselink 1987 は Oort/ Plaut RR Lyr データを再解析して c/a = 0.6 とした。Morrison, Harding 1992 のバルジ方向 K 巨星の観測は少なくとも内側ハローが著しく平坦であることを 示している。他の観測はハローの密度分布が複雑であることを示唆している。 Hartwick 1987 は低メタル RR Lyr の分布が少なくとも二つの成分を要求している ことを示した。近傍の 90 % は c/a ∼ 0.5 の平坦成分に属し、残りが ほぼ球形の成分に属している。Preston et al 1991 が指摘したように内側ハロー が平坦である証拠は Kinman 1965 が見出した。Kinman, Wirtanen, Janes 1966 は ハローの軸比が半径と共に増加して行くと考えた。E/T 円盤の低メタル RR Lyr が 彼らのサンプルに混入した可能性はある。Sommer-Larsen, Zhen 1990 は近傍の 低メタル([Fe/H] < -1.5)準矮星に対して類似の結論に到達した。Sommer-Larsen の 1986 モデルから導いたポテンシャル内の軌道を積分して、彼らは近傍星の ∼ 60 % を比較的球対称な種族(c/a ∼ 0.85) に属し、残りは平坦(c/a ∼ 0.4) な軌道を持つとした。彼らは密度則として r-3.3 を得た。 しかし、このモデルは依然として Ratnatunga, Freeman 1989 が観測した遠方 K 型 巨星の小さな速度分散を説明することが出来ない。

　３．３．２．「標準」モデルのパラメター　

　円盤と同様、「標準」モデルのパラメターは最新のスターカウントモデルと 合致する。ハローの光度関数は円盤と同じであり、主系列は Mv = +4.5 で終わり、その先は球状星団の光度関数につなげている。規格値は 0.15 % とした。主系列と巨星の色等級図は M3 のそれを使った。
ハローの観測的研究の大部分がべき乗密度則を採用しているのに、スターカウント では通常ドボークルーの r1/4 楕円体、Re = 2.7 kpc　 de Vaucouleurs 1977、が使われる。これはべき乗則 r-3.3 に近い。 われわれの「標準」モデルでは表2に示すように　c/a = 0.85 の単一成分ハローを 採用した。

表２．スターカウントから導かれたハローパラメター

　



図２a.　北銀極方向の観測 [V, (B-V)] 色等級図。Majewski1992 BJ, RF観測

図２b．「標準」モデルによる予測。○＝古い円盤。■＝E/T円盤。×＝ハロー

表3A. SA 57 (北銀極)方向のBJ, RF スターカウント

　３．４．「標準」モデルと SA 57 データとの対比　

北銀極方向の色等級図　

　図２a. は、Majewski1992 による観測北銀極方向の [BJ, (BJ - RF)] 観測データを変換した [V, (B-V)] 色等級図である。変換式は Majewski1992 を採用した。そこには明るい星の関して個々のデータが表となっている。
　図2b は「標準」モデルの予言である。Kron 1980 が指摘した二本の帯がはっきり見える。 赤い方は円盤の星である。青い方はより遠方のハロー星(Gilmore 1981)である。この点は 色等級図の暗い方を理解するのに重要なので少し解説を加えよう。

色等級図の二本の帯　

　ある副種族に属する星の距離分布は密度則と体積(Ωr3/3)の掛け 合わせである。その結果、異なるスケール高を持つ円盤、E/T 円盤、ハローは図 3 に 示される通りはっきり分かれる距離分布を示す事となる。古い円盤は中間値 ∼ 700 pc のまわり, (m-M) ∼ 9 ±1.5 に集中し, 一方ハローはもっと広い 距離範囲に跨っている。従って、見かけ等級の暗い円盤星を集めると、それはほぼ 確実に絶対等級で暗い星を集めていることになる。ところが、ハローでは V ≈ 22 でさえも星の分布は依然として Mv = +4 ∼ +6 のターンオフ星 が支配的である。
何故、ハローでは主系列のターンオフより下が効かないのだろう？
V = 17 では典型的な古い円盤星は Mv = +8 の早期 M 型矮星であるが、V = 22 では光度関数ピークの Mv = +12 が主になる。 Mv ∼ +18 までの等級指標として鋭敏なカラー (V-I) を使うと、 この Mv の変遷がはっきり分かる。見かけ等級が暗くなって行くと、 平均カラーが次第に赤くなって行くからである。(B-V) の場合はカラー 1.6、 Mv ∼ +8 で飽和してしまうので、V = 17 より下で赤くなるのは 止まる。
　図2a 中の青い帯の端はハローのターンオフカラーを示し、 V = 21 まで一定値 (B-V) = 0.4 をとる。これより暗い領域では端値は不確かになるが測光の不定性 として理解できる。

表3B. SA 57 (北銀極)方向の B, V スターカウント


図3．「標準」モデルによる円盤、E/T 円盤、ハローの距離分布。
　　　ハローは 4.5 < Mv < 6.5, E/T 円盤は 7 < M v< 9 の星に対してである。
　　　同じ見かけ等級に対し絶対等級差 2.5 は距離 100.5 倍に相当する。
　　　しかし、絶対等級を変えても分布の形は同じである。古い円盤の距離巾
　　　の狭さと、ハローの距離範囲の広さとの対比に注意せよ。


モデルと観測の比較（１）等級分布　

　図４a ではこのモデルで予言される積分カウントを観測と比較した。観測値 の明るい側(V < 18) は Reid 1990 の Oschin Schmidt データである。これは Stobie, Ishida 1987 による木曽シュミットデータとよく一致する。ただ、彼ら のデータは区切りが 0.5 等で粗い。暗い方は Majewski 1992 からとった。彼の データは V < 19 になると星数が少なすぎてしまう。18 < V < 20 領域は従ってより丁寧な解析が必要な箇所だがあまりなされていない。それにも 拘らず、V ∼ 20.5 まではモデルとデータの一致は良い。
副種族毎のモデル線がデコボコするのはどうしてだろう？

モデルと観測の不一致（２）カラー分布　

　上の一致はカラー分布に移ると怪しくなる。不一致は次の２点、つまり モデルは暗い等級で赤い星の数を過小予言し、逆に暗い等級で青いハロー 星を過大予言する点にある。
表４B にモデルと観測の違いを数値で示した。表では V = 18 から 21 の間を 1 等の区分に分けて、各等級区間毎にカラー範囲 (B-V) = 0.3 - 0.6, 0.8 - 1.1, > 1.4 にある星の数（deg-2）を載せた。広い言い方 をすると、青い方にはハロー星、赤い方に円盤星、中間に E/T 円盤星が属する。 標準モデル(モデル a) は 50 - 100 % 青い星を多く予言し、赤い星は観測値の半分しか 予言していない。

明るい(V < 17.5)星のカラー分布　

　カラー分布を詳細に見てみよう。明るい方、V < 17.5 では、観測された青ピーク はモデル予想より 0.15 等赤い。モデルでは青い縁はハロー種族のターンオフカラー 、つまり M3 のターンオフカラー、で決まっている。このズレは以前にも Bahcall et al 1985 で指摘されていた。一般的にはこの問題は高メタル星団47 Tuc の 色等級図を採用することで解決される。しかし、それは銀河面から 5 kpc 以上 離れたハロー星に [Fe/H] ∼ -0.7 を要求することを意味する。これは、近傍の 準矮星のメタル量 [Fe/H] ∼ -1.3 から -2 （Laird et al 1988）と矛盾する。 その上、 図４b,c にプロットされた E/T 円盤の分布は、47 Tuc 色等級図でさえも 観測ピークより青い方に来ることを示している。４．２．２節を見よ。

表４Ａ. 様々なモデルのパラメター
　　　　(8) は古い円盤で Mv < 9 成分。(9)はMv ≥ 9

より暗くなると。　

　暗くなるとモデルは強い双耳峰的カラー分布を予言する。それは実際には V = 20 まで下らないと現れない特徴である。その原因は二つある：
（１）モデルが予言するハロー星が多過ぎる。そのため
　　　　に青いピークが強くなり過ぎる。
（２）18 - 20 等では数多い E/T 円盤の星が二つの
　　　　ピークの間を埋め、青いピークは相対的に
　　　　目立たなくなる。

以前のモデルは明るい所でのみ合っていた　

　以前のモデルが明るい (V ≤ 17) 所でスターカウントとよく合っていたのは、 明るい星は主に古い円盤種族だったからである。例えば、 Bahcall, Soneira 1984 のモデルは Basel サーベイ (V &le, 17.2, Bahcall et al 1985) データとよく合っ たのである。不一致は V > 18 で明らかになってくる。しかし、それは乾板測光 の不定性で覆い隠されていた。新しい、深い SA 57 測光により、「標準」モデルは 銀河系構造を十分に上手く表現していないことが明らかになってきた。
表４Ｂ．みかけ等級区分内でのモデルカラー分布。一番上が観測値。



図4a. 実線＝標準モデルの北銀極方向積分スターカウント。
　　　△=古い円盤、■=E/T円盤、×=ハロー成分。若い・中間円盤は効かない。
　　　V < 18 は Reid 1990, 暗い方はMajewski 1992。エラーバーはポアッソン。


図４b,c. 明るい二つの等級区間での木曽データとモデルのカラー分布の比較。



図．４d-g. 暗い方の四つの等級区間での Majewski データと「標準」モデルのカラー 分布の比較。青いところで過大予言、赤い方で過小予言していることに注意。



　４．標準モデルを再検査　

　この論文の目的は現在のモデルが SA 57 データと合わないことを示すことである。 一方向のデータから決定的なパラメターを得ることは無理である。しかし、現在の データから潜在的な問題を明らかにし、重要なパラメターに制限を加えることは 可能である。ここではその精神で新しいモデルを論じる。

　４．１．ハローの問題　

　「標準」モデルは観測されるより多いハロー星を予言してしまうことが明らか になった。ハローを減らす方法は３つ考えられる。以下で、それらを検討しよう。

　４．１．１．光度関数の変形　

ターンオフ星がスターカウントを決めている　

　「標準」モデルでは、ターンオフより暗いハローの光度関数には Wielen, Jahreiss, Kruger 1983 の WJK 円盤光度関数 Φ(Mv) を使った。 これは Mv = +4.5 ∼ +8 では光度関数が平坦であることを意味する。 これを、広い距離範囲(図２)と結び付けると、V < 23 ではスターカウントが ターンオフの２等以内の星で占められることが判る。

（ 試し算をしてみた。緩い密度勾配が要求されるが？）

しかし、近傍の固有運動星は光度関数のゼロ点を決めているのだが、それらの絶対 等級は Mv > 7 で暗過ぎる。これらの星の観測ではターンオフ付近 の星の数密度に制限を付けられない。明らかに、 Mv < +6 での ハロー光度関数を下げるとハローの予想星数を低下させる。

球状星団の光度関数　

　ハロー光度関数の形は球状星団の光度関数からも決められる。しかし、観測は 暗い星に集中していて我々の目的に合わない。大部分の観測は星団周辺部の 小領域を深く測光している。そのためターンオフ付近の星は１０から２０個程度 しか入らない。我々はまた、様々なデータを Mv = +6.25 で規格化 しなければならなかった。ターンオフ光度 Mv = +4.5 では進化効果 が効いているからである。

球状星団データ　

　図５では球状星団の観測データを、Yale, VandenBerg/Bell 恒星進化モデルから 導いた光度関数、Dawson 1986, Bahcall.Casertano 1986 近傍星解析結果と比較 した。Sandage 1957 が行った M3 全体の測光を行った光度関数、 Wielen, Jahreiss, Kruger 1983 の WJK 円盤光度関数、我々の標準モデルで採用した 光度関数 Φ(Mv)と比較した。各図には Φ(Mv)と　 Sandage M3 データを書き込んである。

球状星団の平均光度関数　

　Mv ∼ +3.5 より明るい星は深いスターカウントでは効かない。 しかし、 Kraft 1989 が述べたように、Sandage 1957 の M3 光度関数は他の 観測と較べると大きな値を示す。その中には Paez et al 1987 の星団外側部の CCD 観測を含む。Sandage 1957 データはパロマー5m鏡を用いた星団全面の観測 結果である。Gilmore,Reid 1983 による南銀極のデータ、Hartwick 1983 の フィールドサーベイを説明するため、Kraft 1989 は M92/NGC5053/47Tuc 光度 関数（Sandage の M3 でなく）に M3, M5 のヘス図を採用する必要があることを 示した。
ヘス図をカラーで積分すれば光度関数になるが、 適合しているのか？
赤色巨星枝下部の密度は Preston et al 1991 が求めた近傍水平枝星の数、Friel 1987 が述べた Serpens フィールドでのハロー巨星の欠如、それから 恒星進化 モデルの予想と良く合う。 		球状星団と近傍星の差　

　様々な球状星団を比較すると、+3.5 < Mv < +7 では互いに 良く合っている。例外は Pal 5 である。この星団はほぼ動径方向の運動をする 遠方星団で激しい力学進化を遂げて光度関数は Mv ∼ +6 で ピークを形成している。球状星団の平均光度関数は WJK 関数と違い、 +4 < Mv < +6.5 で平坦にならない。こうして、 Mv = +6.25 で規格化しているのでターンオフ密度を半分くらいにしている可能性がある。

標準モデルは明るい星が足りない　

　この結果は「標準」モデルで採用したハロー光度関数が明るい側で激しく落ちる という特徴とは大きく異なる。N(Mv=+3):N(+4.5):N(+6.5) は「標準」 モデルでは 1:60:60 だが、図５e に示した改訂版(３球状星団の平均)では 2.5:24: 60 である。47 Tuc は図５の中では最も高メタルでターンオフ付近に突然ピークを みせているが、ハローテンプレートとしては不適当なこの星団でさえも、1.5:23:60 である。

準矮星光度関数　

　図５a には Dawson 1986 の準矮星を、５e には Bahcall, Casertano 1986 の 準矮星光度関数を示した。Luyten Half-Second Catalogue (LHS) データ (Luytren 1976) の最も明るいビンは区間 3.0 < Mv < 6.6 を含み、Bahcall, Casertano 1986 光度関数は規格値 = 0.35 % である。どちらも、Mv < +7 では WJK 円盤光度関数よりも球状星団光度関数に近い。

球状星団光度関数を「標準」モデルに組み込む　

　球状星団光度関数を「標準」モデルに組み込むと、SA 57 方向でのハロー星の予想数 を大きく減少させる。表４(モデルb) は青い星の予想数への効果が示されている。 数値は観測の 2σ 以内(ρ0(ハロー)＝0.15% × ρ(円盤),c/a = 0.85で)に入る。 V = 18, 20 での (B-V) カラー分布は図６a, b に示されている。


図５e．▲ = 準矮星、○ = 球状星団の平均光度関数。 (a) の標準 モデル、M3も参考に描いた。


図５．ハロー光度関数の評価。
(a): 上ヒストグラム＝円盤光度関数。規格値=0.15%、 下ヒストグラム＝標準モデルのハロー光度関数、白丸＝Sandage 1957 の M3 光度 関数。円盤光度関数と Mv = 6 - 7 で合うよう規格化、クロス＝ Dawson 1986 の 近傍 LHS 星に基づく光度関数。
(b). ▲ = NGC 5053([Fe/H] = -2.58), □ = M92(-2.24), × = M3(-1.66), ☆ = 47 Tuc(-0.71) の光度関数。(a) の円盤、標準モデル、M3(違う出典)も参考に描いた。
(c)　△ = M12([Fe/H]=-1.61), □ = M10(-1.60), × = M68(-2.09) (a) の標準 モデル、M3も参考に描いた。
(d)　△ = M5([Fe/H]=-2.40), □ = Pal 5(-1.47), × = M30(-2.13) (a) の標準 モデル、M3も参考に描いた。


　４．１．２．光度関数の規格値を変える。

ハロー運動学から規格値が決まる　

　規格値はもろにハロー星数を変化させる。図６c, d （表４ モデルc）は規格値を 0.085 % にした場合、フィットが改善される様子を示している。3.3.1.節に述べた ように、この量は固有運動星データから導かれた。RR Lyr や　水平枝星も規格値 0.15 % - 0.20 % の範囲を支持している。固有運動サンプルの解析には、それが 横速度から Schmidt 1975, Richstone, Graham 1981, Bahcall, Casertano 1986 か、固有運動図から Dawson 1986 かによらず、ハローの運動学のあるセットを 選ぶ必要がある。運動学が与えられると、モンテカルロ計算によってハロー準矮星の どのくらいの割合がサンプルに含まれるかを評価できる。その次にそれから近傍密度 を導ける。

どんなハロー運動学を採用するか？　

　しかし、固有運動検出の限界距離は横速度 VT に比例するから、推定 される局所数密度は ⟨VT3⟩ に比例する Reid 1984 。　？　
こうして、密度推定はハローにどんな運動学を採用するかに強く依るのである。実際、 これが Bahcall, Casertano 1986 がハロー星近傍数密度を 9.5 × 10 -5 pc-3, または規格値 = 0.37 % とし、一方 Dawson 1986 が 0.17 % とした原因である。
　採用した速度分散はサンプルの分散からチェックされ ないのか？　

運動パラメターの影響　

　我々は、採用したハロー運動学が導出されるハロー対円盤比にどう影響するかを モンテカルロ法で調べた。表５には代表的な運動学パラメターに対して Dawson の LHS 発見率がどう変化するかを示してある。これを見るとシステムの平均回転速度 が非常に重要なパラメターであることが判る。
　Bahcall,Casertano 1986 による LHS データの解析は、かれらのハロー運動パラ メターの結果、発見率を下げ、結果として表５Ｂ行のようにハロー規格値を倍増させた。 RR Lyr 星（A,C 行）、準矮星(D,E行), 低メタル巨星(F行)の解析は、ハローの回転 速度 = 20 - 40 km/s を想定し、ハロー規格値 = 0.17 - 0.25 % を導いている。一方、 二つの深い固有運動サーベイからのハロー運動学を用いた（表５ G, H 行）規格値は 0.11 - 0.13 % である。 		規格値を低下させる解決法は無理　

　しかし、規格値を 0.085 % （もし「標準」モデルのハロー光度関数を維持したけ れば必要な値）まで下げるには、表５ I, J 行に見るように、極端に「熱い」ハロー 運動学が必要とされる。もし、普通の速度分散（RR Lyr をトレーサーとして）を 採用するなら、太陽運動の V ∼ -325 km/s, 100 km/s の逆回転、が必要となる。 一方で、Majewski 1992 からの僅かな逆回転運動でさえも、どんなハロートレーサー にも見られないほどの大きな速度分散を要求する。このように、ハロー規格値を 単純に変更して「標準」モデルを観測と合致させようとする試みは他の深刻な 不一致を招く。


表５．近傍ハロー星の「LHS発見率」(Dawson 1986)へのハロー運動学の影響。
(2)-(4)列 = 太陽運動。(5) - (7)列 = 速度分散。(8)列 = 300 pc 以内で LHS 基準 (μ > 0.5"/yr)にかかる割合（%)。(9)列 = ハロー対円盤の比
A：低メタル RR Lyr 統計視差(Woolley 1978)。B：Bahcall,Casertano 1986
C: 低メタル RR Lyr 統計視差(Strugnell 1986) D:準矮星の運動 Norris 1986
E: 低メタル巨星 Carney,Latham 1986。 F: 低メタル巨星 Morrison et al 1990
G: ハロー太陽運動は Majewski 1992の SA 57 固有運動研究から。
H: ハロー太陽運動は Reid 1991 の 北銀極 固有運動研究から。
I, J : 「標準」モデルをスターカウントにフィットさせるにはこんな運動



図６．予想値を観測に近づける幾つかの方法。
　　　(a), (b) 球状星団光度関数をハローに使った（表４　モデルb）場合。V = 18 - 19 と V = 20 - 21。
　　　(c), (d) 「標準」モデル光度関数だが、規格値 = 0.085 % に下げる。表４　 モデルc。
　　　(e), (f) 「標準」モデル光度関数、規格値 = 0.15 % 軸比 c/a = 0.6。表４　 モデルd。


　４．１．３．ハロー密度則の変更による解決策　

平坦なハロー　

　Z ≥ 5 kpc のハロー星の数を減らすには密度分布の勾配を急に変えるか、 c/a 比を平坦にするかである。我々には一方向のデータしかなく、他の 観測が r-3.5 よりは緩い密度則を示していることを考慮して、 軸比を変化させることにした。しかし、一方向のみでもハロー分布に関して 幾分の制約を課すことができる。というのは、スターカウントは V = 18 - 21 で増加することを要求しているからである。こうして、軸比 c/a = 0.6 とする ことで V = 18 -20 で星数を増加させて「標準」モデルと観測の折り合いを つけた。しかし、このモデルだと V = 20 - 21 では青い星の数が過小予想に なる。図６e, f、表４モデルd を見よ。つまり、スーターカウントの勾配が 要求しているのはハロー星のかなりの部分は c/a = 0.8 の成分に入っている ということである。

二重ハロー　

　軸比 0.8, 球状星団光度関数、規格値 = 0.15 % （表４B, モデル g - l）の モデルは観測と 1 σ で合う。予想されるように、規格値と軸比は逆相関する ので、軸比 0.85 は表４モデル l と適合する。
このあたり良く分からない。直訳する。
これらの規格値は表５にリストされている値（行A,C,D,E）と一致しない。しかし、 もし希望ハロー星のかなりが c/a ≤ 0.5 となる軌道を取っていればそれらは Z > 6 kpc の密度には寄与しない。言い換えれば、スターカウントデータから 我々が推定する規格値はハローの球対称成分のみを反映しているのである。具体的 な例を挙げよう。もし Sommer-Larsen, Zhen 1990 の議論を受け入れて、近傍ハロー 星の 40 % が平坦ハローに属すると仮定すると、我々の結果はハロー星の規格値 は 0.20 - 0.25 % となる。表４モデル k はこの二重ハローモデルを採用している。 しかし、Hartwick の２成分ハローは(表４モデル e )規格値 0.3 % だが準矮星の 10 % だけを球対称成分としており、観測とは合わない。

E/T 円盤の影響　

　3.3.1 節では Wyse, Gilmore 1989 が北銀極方向と l = 272°, b = -44° 方向の２個所での 18 < V < 20, (B-V) < 0.6 星を比較して c/a = 0.6 を導いたことを述べた。Gilmore et al 1989 は Kron SA 57, SA 57 データから 導かれる軸比を無視した。この等級区間には E/T 円盤とハローの双方が寄与する ので c/a を導く前にまず E/T 円盤の割合を決めておかなくてはいけない。後で 述べるが、南銀極と SA 57 データの再解析からは、Wyse/Gilmore 1989 が採用した よりは大きな E/T 円盤のスケール高と規格値が示唆される。その場合、円盤が 青い星に大きな寄与をなし、高銀緯と低銀緯との間の観測値の比を下げる。4.3.節 で述べるモデルを使うと、円盤星の混入を許して彼らの得た観測軸比 0.59 はハロー 軸比　0.75 - 0.8 と適合する。



　４．１．４．ハローモデルのまとめ　

　限られた範囲でパラメター空間を探った結論はスターカウントデータを解釈する 際に決定的なのはターンオフ付近での光度関数の形である。ハロー光度関数の Mv > +8 の部分はスターカウントでは無視して構わない。表４の モデルのどれも観測と合うものは無かった。特に重要な特徴は V = 18.5 と 19.5 では殆ど同じ数で V = 20.5 になると倍に跳ね上がることである。しかし、もし 球状星団光度関数をハローのフィールド星に適用すると、軸比 0.8 ±0.05, 規格値 0.15 ±0.03 のモデルで SA 57 データを 1 σ 内でフィット できる。ハローの多成分モデルが正しいならハロー準矮星の近傍密度はより大きく なる。

　４．２．円盤の問題　


Kuijken, Gilmore 円盤は暗い方で赤い星が欠損　

　「標準」モデルでは、ハローと逆に、暗い等級での円盤の寄与は過小に評価され ている。同じ欠損は Sandage 1987, Kuijken, Gilmore 1989 の円盤パラメターを 用いたモデルで見られる。3.2.1 節に述べたように、後者は南銀極方向での K 型 矮星の空間分布を調べ、古い円盤に対してスケール高 249 pc、E/T 円盤に対し 1000 pc、 近傍での相対比を 96 対 4 とした。図７と表４モデルg はこの パラメターのモデルは暗く V > 19 赤い矮星の数がファクター３欠損している ことを示す。

Sandage 円盤は高 z で急落し過ぎ。 　

　Sandage 1987 の垂直密度分布は Kapteyn 1922 の式、速度分散 σw を密度 D(z) に関係付ける、から導かれている。Sandage は Saio, Yoshii 1979 の速度分散を用いた。 この式だと低 z では比較的ゆっくり密度が低下し、 高 z で指数関数的に落ちる。従って、古い円盤星 ( σz = 17 km/s) は初めに 1/e に落ちるのは 270 pc かかるが、先の方ではスケール高が 150 pc になる。それは E/T 円盤に対して 940 pc と 635 pc (σz = 42 km/s), ハローでは 3200 pc と 2850 pc (σz = 90 km/s)である。相対規格比は 200:22:1 で, 銀極方向の Mv = +4, (B-V) = 0.3 - 0.6 星に合うよう定められた。観測は Gilmore, Reid 1983, Fenkart 1966, Yoshii et al 1987, Becker, Fenkart 1976 による。 Sandage に従い、我々も E/T 円盤に 47 Tuc でなく近傍星 CMD を用いた。 		結果は 図８、表４モデルh に示した。 V = 15 - 17 ではカラー分布のフィットは良いが、 暗い方では急落下の密度則のため M 型矮星の数が不足する。
この様に、現存モデルはどれも SA 57 領域の深い測光観測をフィットできない。 次の節で円盤の密度則を再考する。

　４．２．１．円盤の密度則　

Gilmore, Reid 1983 カラー等級関係に問題あり　

　標準モデルで採用した古い円盤のスケール高 325 pc は Gilmore, Reid 1983 の図５に示された結果に基づいている。密度則は南銀極データに [Mv, (V-I)] 関係を適用して得た測光視差から導かれた。Stobie, Ishida, Peacock 1989 は Gilmore, Reid 1983 に使われたスプラインフィットは最近の三角視差星に対する 結果には良く合わないと指摘している。実際、K, M 型矮星に対する CMD は、

　　　　　　　Mv = 2.89 + 3.37(V-I),　　　(V-I) > 0.92

で表わされる(Stobie,Ishida,Peacock 1989, Reid 1991). もっと明るい所では、

　　　　　　　Mv = 1.10 + 5.33(V-I),　0.5 > (V-I) > 0.92

が良い近似となる。この関係は太陽メタル量のものであることに注意。


図７．Kuijken, Gilmore 1989 の古い円盤、E/T 円盤スケール高を採用し、 標準ハローを付けたモデル。暗い方で円盤星が欠損することに注意。



図８．Kuijken, Gilmore 1989 の古い円盤、E/T 円盤スケール高を採用し、 標準ハローを付けたモデル。暗い方で円盤星が欠損することに注意。




図９．南銀極方向 Gilmore, Reid 1983 測光データに測光視差を適用した密度分布。 黒点＝観測値。２本の縦線＝サンプル中最低 L の星が V = 19.5 と 20.0 になる距離。 観測値から 325 pc スケール高の古い円盤と、3500 pc スケール高、規格値 0.15 % の指数関数ハローを引いた。残差を△で示した。高度 1.2 - 5 kpc 部分に明瞭な 密度超過が認められる。それを眼で合わせてスケール高と規格値を表６Ａに示した。


巨星の混入は無視できる　

　こうして、改訂された測光視差を基に南銀極データから垂直密度則を再導出した。 図９がそれである。ただ、まずハローの混入を調べる必要がある。そもそもどんな 測光視差でもサンプル星が一定のカラー等級関係に従うことを仮定している。我々 のケースでは、サンプルの支配成分は矮星と仮定している。この仮定は Bahcall 1986 には疑問視された。しかし、我々は自分たちのモデルを用いてこの仮定が正当である ことを示した。図１０はMv < 3.5 のハロー巨星から予想される色 等級図が示されている。データは表４モデル k から採った、立体角 10 平方度に 対するものである。図中の縦線は、矮星の Mv = 5.5 と 6.5 に対する (V-I) カラーである。これを見ると巨星の混入が少ないことが明らかに判る。すな わち、見かけ等級 V = 13 - 18 区間では 5 星/deg2 であり、一方 観測星は V = 13 - 14 で 5.6 星、17 - 18 で 33.0 星である。このカラー区間は M3 巨星枝の底に当たり、絶対等級 0 から +2.5 の間に相当する。ハロー巨星 の表面密度が少ないことを支持する観測結果は、Ratnatunga, Freeman 1989, Kuijken, Gilmore 1989 の K 型星サーベイからも得られている。前者のサーベイは (B-V) > 0.9, または Mv ≤ 0 に限定されているが、60 平方度内にたった 150 巨星を見つけただけであった。一方、後者はもっと大きい (∼ 25 %) 巨星 /矮星比を V < 16, )B-V) < 1、つまり r < 1 kpc、与えているが、それ でも巨星の混入は数 % 以下である。 　

駄目押し　

　この点をさらに強化するため、図９b 0.83 ≤ (V-I) < 1.07 の星が r = 3 kpc で遠方の巨星であるとしよう。その場合巨星は矮星より 4 等明るいので、 距離をファクター 6 小さく見積もっていたこととなり、密度を 63 大きく見積もっていたことになる。これは r = 18 kpc で密度 10-7 pc-3 に相当する。密度則 r-3.5 によると、近傍密度は ∼ 3 × 10-6 になる。
近傍は r 幾つに対応するのか？(18/301/3.5) kpc
図５e　から判るように Mv < +2.5 の星の近傍密度は 2 × 10 -7 であるから、観測と一致させるためにはハロー星の密度を１０倍 大きくする必要がある。

表６．南銀極の密度分布



図１０．Mv < 3.5 のハロー巨星から予想される色等級図。
表４モデル k。球状星団光度関数、軸比 0.8, 規格値＝0.15 % を仮定。縦線 は Mv = +5.5 と +6.5 に対応する。


ハロー星の混入　

　ハロー星の混入は青いカラー、4.5 ≤ Mv < +5.5, 0.64 ≤ (V-I) < 0.83 ではより強い。しかし、そこでさえも、V = 16 - 17 で 3 星 deg-2 で、観測される星密度 27.6 星 deg-2 よりずっと少ない。この等級区間は距離に直すと少なくとも 2500 pc に相当し、 　 2500 pc は DM = 5 log 250 =12 だから、Mv = 4 - 5 　図９の密度勾配が生じるその先になる。だからハロー星はこの勾配変化 の原因ではない。このカラー領域で、影響は小さいものの増加するハロー星の寄与 は準巨星段階での寿命が巨星段階に較べて長いことに起因する。しかし、(V-I) > 1.1 での巨星の混入は、もし 47 Tuc 型の高メタル色等級図を使うので なければ、無視して良い。


図９でサンプル星の限界距離　

　図９には 4.5 < Mv< 9.5 の区間での密度則を示している。 縦マークは各サンプル中で最も光度が小さい（赤い）星が見かけ等級 19.5 と 20.0 になる距離を示している。この２点の間で我々のサンプルが不完全になって いる可能性が強い。特に青い星では I 等級の限界 18.25 等が効いてくる。 もう一つ注意しておくが、明るい Mv< 6.5 の星は遠くまで到達 するが、カラー等級関係が急になるので個々の距離決定は不確かになる。

内側密度分布　

　最初に密度分布の内側部分を見てみよう。データはまあまあの精度で指数関数型 である。z = 0 におけるスケール高と外挿密度は表６に示した。密度値は WJK 光度 関数と広い範囲で合致している。銀河面付近 z < 400 pc での上に反り返る密度 分布は明るい V < 13 所での円盤巨星の混入を示している。平均スケール高は 標準モデルで使った 325 pc に近い。しかし、暗い星では少し大きな値を示している。

密度残差　

　z > 1 kpc になると、Gilmore, Reid 1983 が述べたのと同じ密度勾配の変化が 現れる。古い円盤とハローの寄与を除いた残余が図９に示されている。これら「超過」 星は V > 18 で (B-V) 分布の青いピークの巾を広げ、中間カラーを埋めることで 予言された双峰性を弱め、より暗い方で赤いピークに寄与する。「超過」星は中間 等級 V = 15 - 17.5 では青い (B-V) < 1 星の主な供給源である。E/T 円盤の 密度は z = 5 - 6 kpc に達するまではハローに対して予言された値に達しない。 この高度は丁度 Majewski 1992 が運動特性と紫外超過の分布が急変し、彼をして その先はハローが支配的になると示唆させた高さである。

「超過」円盤のスケール高　

　図９を見ると、E/T 円盤は「標準」モデルより大きなスケール高と規格値を持って いるらしいと判る。表６は指数関数を図９ a - d にフィットした時のパラメターを 載せてある。規格値は 2 - 3 %, スケール高 1300 - 1700 pc となる。暗い星で スケール高が大きくなるのは距離の限界が短くなるためかも知れない。現在のスケール 高はしかし、最近の短い 1 kpc 以下のスケール高よりは Gilmore, Reid 1983 が初め に出した 1350 - 1450 pc に近い。ただし、我々が Gilmore, Reid 1983 と同じ データセットを使用していることを注意しておく。

表６．南銀極方向の密度分布


後で議論するが、北銀極と SA 57 方向の両方のカウントは、特に 14 - 17 等で、規格値　2.0 - 2.5 % を 使った方がフィットが良い。それにも拘らず、古い円盤と E/T 円盤の表面密度を 計算すると少なくとも 10 % は広がった成分に属することを見出すのである。


　４．２．２．E/T 円盤のカラー等級関係　

メタル勾配　

　ここまでに導かれてきた密度則は単一の [Mv, (V-I)] 関係に 基づいている。これは銀河面垂直方向にメタル量勾配が存在しないことを暗黙に 認めていることである。しかし、広がった円盤も厚い円盤もメタル量勾配を 認めている。広がった円盤では、Norris 1987b は円盤の最も古い星の垂直 速度分散が大きく、それらの星の [Fe/H] ∼ -0.5 かそれ以下とした。一方、 厚い円盤は Gilmore et al 1989, Carney et al 1989 によれば [Fe/H] ∼ -0.6 と特徴付けられている。しかし、最近 Morrison et al 1990 が低メタル [Fe/H] < -1 巨星が円盤と共に回転しているという結果を発表したように メタル量には巾がある。

メタル量勾配の観測　

　メタル量勾配の直接観測は 2 kpc 以内に限定される。 Gimore, Wyse 1985 の CCD UBV データは 1kpc 以内であったし、 Yoshii et al 1987 の紫外超過 観測、彼らは -0.5 ±0.1 dex/kpc と出した、は 2kpc 以内である。最も 広範なサーベイは Yoss, Neese, Hartkopf 1987 の K 巨星サーベイと Majewski 1992 の SA 57 領域の紫外超過観測である。前者は z = 700 pc まで -0.4 dex /kpc、その先 z = 8 kpc まで -0.18 dec/kpc という勾配を導いた。それらでも z > 2.2 kpc では星の数は少ない。平均値の周りの分散も大きく、z = 3 kpc でも太陽メタルの星が見つかる。もっとも,　その星に対し、Norris,Green 1989 は低いメタル量を与えている。SA 57 データもやはりメタル量の大きな分散 を与え、6 kpc 以内ではもう少し緩やかな勾配を示している。 z = 2.5 - 5 kpc での平均メタル量は [Fe/H] ∼ -0.4 (δ0.6 ∼ 0.1) である。5 kpc より上では、厚い円盤とハローが合うところだが、高メタル星が 急に消える。

メタル量変化と等級変化　

　メタル量勾配を加えると密度則の何処が変わるだろう？我々は、-0.25 dex/kpc と -0.10 dex/kpc の二つで南銀極密度分布を計算し直した。どちらの計算でも メタル量下限を　-1.0 とした。低メタル星 [Mv, (V-I)] 関係は 近傍星と較べ下にくる。しかし、Laird et al 1989 は紫外超過 δ0.6 とサブ光度 δMv の関係を沢山導いた。我々は Carney 1979 の較正を用いる。図１１a は (B-V) = 0.7 - 1.1, Mv = +4.5 - +7.5 での結果を示す。 簡単には以下のようになる。

　　　　　　　δMv = -0.87δ[Fe/H]

急なメタル量勾配はスケール高を増大させる　

　これらの再計算の結果で最も重要なことは大局的な形態は図９から変化しないと いう点である。古い円盤は実際変わらない。z が上がると低光度の影響が密度増加 として現れ、平坦な円盤へ導く。-0.25 dex/kpc では E/T 円盤のスケール高が　 2 kpc を上まわる（表６c）。図１１b の指数関数フィットはスケール高 2500 pc, 規格値 = 3 % である。この値では E/T 円盤は青いカラーで V > 14 で支配的と なる。このモデル（表４モデル i ）は明らかに受け入れがたい。

小さいスケール高　

もっと緩いメタル量勾配はもっとフィットが良い。ただしこの場合も E/T 円盤 スケール高と規格値は暗い星で大きくなる。表６Ｂ と図１１ c, d を見よ。 メタル量

表７．主系列星のカラー等級関係


勾配のない（図９）場合のように、スターカウントは小さいスケール高 と低い規格値を推奨する。表４モデル j は 6.5 < Mv < 8.5 の 解析に直接基づく E/T 円盤を使うと、青と中間カラーの暗い星を多く予言し過ぎ ることを示す。

矛盾はあるが、緩いメタル量勾配は確かだろう。　

　これら異なる絶対等級間の矛盾が Gilmore, Reid 1983 データとその較正に 問題があるのか、それともモデルの不十分さ、例えば単純過ぎる密度則、が 原因かはもっと精度の高いデータを待たなくてはいけない。しかし、現在の解析 でもメタル量勾配を急にし過ぎるとおかしな結果になることは判る。したがって 比較的緩いメタル量勾配がよいことは確かであろう。

新しいメタル量に対する色等級図　

　メタル量勾配が与えられたら、つまり幾つかの成分の和として表わすのだが、 E/T 円盤の色等級図を考え直す必要がある。２成分指数関数近似で円盤の密度 を表わす限りでは、図３を見ると、古い円盤星は z ∼ 700 pc から 主に採ってこられ、E/T 円盤は z ∼ 2 - 3 kpc からである。平均メタル 勾配 ∼ -0.1 dex/kpc では E/T 円盤星に　-0.3 から -0.4 dex を付与する ことになる。これは 47 Tuc の [Fe/H] ∼ -0.7 より大分高い。図４c,図７c を見ると 47 Tuc 色等級図の E/T 円盤は V = 17 では少し観測より青すぎるのも このメタル量の結果そ支持する。その上、平均 [Fe/H] = -0.4 は Majewski 1992 の UBV 測光、Friel 1987, Hartkopf,Yoss 1982, Ratnatunga,Freeman 1989 の 分光とも合致する。もっとも、Carney et al 1989 は [Fe/H] = -0.5 を導いた。


図１１．(a): Laird et al 1989 の紫外超過対 δMv 関係から導いた メタル量とサブ光度の関係。シンボルは(B-V)を表わす。△は(B-V) = 0.7, 星が(B-V)=1.1 である。実線＝我々が使った関係。
(b): メタル勾配 -0.25 dex/kpc を仮定した時の、南銀極方向の密度則。シンボル は図１０と同じ。残差に指数円盤をフィットするとスケール高 2500pc, 規格値 3 % となる。
(c), (d) : メタル勾配 -0.1 dex/kpc を仮定した時の、南銀極方向の密度則。E/T 円盤に付与したパラメターは表６Ｂにある。



　４．２．３．円盤のまとめ　

　南銀極方向の密度則を振り返って、我々は少なくとも Mv < +8 の星が 示す古い円盤は平均スケール高 ∼ 325 pc の指数型分布で良く表現さ れることを見出した。これはメタル量勾配を仮定しなくても、-0.25 dex/kpc という大きな勾配を採用しても成立する。しかし、後者の場合は古い円盤と 		ハローの寄与を差し引くと、残差は平坦でスケール高 2 kpc 以上の E/T 円盤 を残す。もっと緩い勾配を使うと、残差のスケール高 ∼ 1350 - 1800 pc, 規格値 ∼ 4 - 2.5 % となる。しかし、 SA 57 データは許容範囲を 1400 - 1600 pc, 2.5 - 2 % にしている。最後に、緩い勾配は E/T 円盤の平均 メタル量 [Fe/H] ∼ -0.4 を導く。したがって、 E/T 円盤に適用する 色等級図は古い円盤と 47 Tuc の中間となる。

　４．３．暫定モデル　

モデルは暫定的なものである　

　スターカウントモデルには多くのパラメターが含まれているので、それらを 丁寧に調整すればどんな観測セットでも合わせられる。深い銀河を除去した 多色、他方向の観測が銀河構造を解きほぐすには必要である。その点、ここで 扱ったデータは予備的で北銀極をもっと良く合わせるためのものに過ぎない。 将来の観測でこのモデルの欠陥が判るだろう。

平坦なハロー？　

　暫定モデルのパラメターは表４モデル k に示した。パラメターの不確定性を 強調するため、もっともな代案としてモデル l - n を示した。図１２には、モ デルの予想を観測値と比較した。ハローに対しては４．１．１．節に述べた球状 星団の光度関数を用い、空間分布はドボークルー回転楕円体、有効半径 2.67 kpc, 軸比 c/a = 0.8, を用いた。観測カウントはハロー規格値として 0.15 % を要求 する。単一でより平坦なハローだと規格値を上げ、密度勾配を緩くしなければな らなくなり(表４モデル d, f )、結果としてデータとの一致は悪くなる。しかし ながら4.1.3 節で述べたように、これは著しく平坦な第２成分の存在を否定する ものではない。例えば、c/a = 0.4, 規格値 0.1 % （近傍準矮星の 40 % を含む） が加わっても、 V = 19 - 20 の間で一平方度当たり 6 - 8 個の星が増えるだけ である。表４のモデル k と m を較べてみよ。こういうわけで、ハローの総規格 値 0.25 %, Sommer-Larsen, Zhen 1990 のと似た軌道分布のモデルはスターカ ウントデータと矛盾せずに提示可能である。

E/T 円盤のパラメターはまだ一意でない 　

　円盤に関してはカラー分布と密度則から広がった成分の存在は明らかである。 規格値、スケール高、色等級図間の調整で観測に合う解は一意に定まらない。 図１２ d と図１２ e は E/T 円盤の分布ピークが V = 18 から 20 の間に来る ことを示す。広い領域に渡る十分なデータが揃えば幾つかのパラメターにより 強い制約を掛けることが出来るだろう。北銀極の深い I バンドデータも密度 分布を解きほぐすのに役立つだろう。しかし、現在のところは E/T 円盤には ４．２．２．節で述べたスケール高 1400 pc、規格値 2.5 %、中間メタル量色等 級図 の指数関数型円盤モデルを採用する。

暗く青い天体の超過は銀河らしい　

　図１２では上の暫定モデルを北銀極観測とフィットした。図には V = 22 より 暗い星と、V = 16 より明るい星のデータも載せた。暗い方は V > 20.5 で モデルとデータが離れて行く。図１２f はモデルが青い星、赤い星の双方で過小 予言して 		いることを示す。青い方では 20 < V < 21 のずれは 15 % であり、 2.2 節によると銀河の混入の影響の可能性が高い。ハローをもう少し平坦にする か規格値を上げるかすると 20 < V < 21 での一致は改善されるが、明るい 方で過大予言することになる。サンプル数が少なすぎるための影響かも知れない。

暗く赤い星の超過。I 測光が大事。　

　データは赤い方でもモデル予想を上回っている。Koo et al 1986 も彼らの SA 57 観測から同様の結論を導いて入りことを注意する。それらの大部分が系外起源 という議論は固有運動観測から否定(Sommer-Larsen, Zhen 1990)された。 　もっと赤い色等級図を使うと E/T 円盤が 19 等より暗い方にはっきり見える赤い ピークに幾分寄与できる。しかし、M 型星の大部分は古い円盤からで、それらの 平均距離指数は ∼ +9 （図３）である。従って対象星は Mv ∼ +9 かより暗い光度が期待される。[（Ｂ−Ｖ）が縮退してしまうので この点に関して断定的なことが言えない。I バンド測光が SA 57 で可能と なると (R - I) カラーにより赤いピーク星の絶対等級を決めることができる だろう。]　 この欠陥を直す方法としては、

（１）光度関数を直す。ただ、近傍で Mv より明るい星が倍増する。

（２）もっと緩い密度則。スケール高を大きくすること。

（３）上の二つを組み合わせる。

表６に載せたスケール高は Mv > +8 ではスケール高が増加する徴候を示す。 ただそれは単に、短距離のデータを使い暗い所で数値を出す不確かさのため かも知れない。いずれにせよ、我々は古い円盤にはスケール高として、Mv ≤ +8 の星で 325 pc, それより暗い星で 400 pc とする。これでさえも、V > 19 では赤いピークの予想値が低すぎる。

総カウント　

　総カウントに関しては銀河の混入(図１)が V > 22 のくらい天体のカウン トを挙げている可能性がある。図１２ h は 22 < V < 22.5 （Kron）の (B-V) 分布を比較している。観測天体の超過はカラーに対し一様に分布している。 ただし、測定誤差は大きい。Mv > +10 での光度関数の形が間違えている、 それらの暗い星の密度則が間違えている可能性がある。I 測光がこの問題の 解決に寄与するかも知れない。実際、将来の進展は多色観測を別の領域でさらに 深く行うことで達成されるであろう。



図１２．暫定モデルが予想する微分スターカウント A(m) とカラー分布。ハローには 球状星団光度関数(図５e)、軸比 c/a = 0.8, 規格値 = 0.15 %。
E/T 円盤は穏やかな低メタル [Fe/H] ∼ -0.4 色等級図, スケール高 1400 pc, 規格値 2.5 %。古い円盤は Mv > +9 の星でスケール高 400 pc を持つ。
シンボルの意味は図４に同じ。比較のため、Kron の 22 > V > 22.5 データ (h)、Stobie, Ishida 1987 の V < 16 (i, j, k) を加えた。

　５．結論　

目的は「標準」モデルの不適切さを示すこと　

　本論文の主目的は、これまで銀河系を表わすのに用いられてきた標準的なモデル と北銀極方向の暗い等級における観測値とがかなり違うことを示す事にある。 V > +18 での総カウントではモデルと観測との一致が良いが、ハロー[(B-V) ∼0.06] の寄与がかなり強く評価され、それに対応して円盤[(B-V) > 1.3] は過小に評価されている。その上、円盤は V = 21 までは主要な種族なのである。

ハローの問題点　

　観測が一方向なので、観測的制約には限りがあるが、解析の結果ハローに関する 問題点は極端に古い種族に対し不適切な光度関数を使用していたことがトラブルの 主要な原因であることが判った。我々は球状星団の観測を使ってハロー光度関数を 決め直した。その結果、SA 57 方向は少し平坦な c/a = 0.8, r1/4 で 規格値 0.15 % ハロー が観測とよく合うことを見出した。多成分ハローももう一つ の可能性である。

E/T 円盤　

　円盤は幾つかの指数型円盤の重ね合わせで表現される。E/T 円盤はスケール高 1400 - 1600 pc で対応する規格値 2 - 2.5 % を持たせれば十分にフィットすることが判った。この値は最近の研究で 提出されている値よりも、当初 Gil,ore, Reid 1983 が提案した値に近い。その上、 北銀極の観測は z ∼ 3 kpc での色等級図が高メタル球状星団　47 Tuc ([Fe/H]∼-0.65) よりも古い円盤のそれに近いことを示している。 		古い円盤　

古い円盤 に関して言えば、 SA 57 V = 18 - 21 等間でのカラー分布に現れる (B-V) ∼ 1.5 での強いピークは古い円盤の Mv > +9 の暗い星のスケール高を少なくとも 400 pc にすることを要求している。強調しておきたいのは、円盤成分を表わす のに幾つかの独立な指数円盤を使ったが、それらが分かれた種族であるとか、それ らがこの関数形に厳密に従っているとかを保持する強い理由はない。

暫定モデル　

　ここに示す暫定モデルが観測によりフィットするが、観測からの制約が十分で ない。SA 57 内では I バンド観測を赤い星の V > 20 まで行い絶対等級を決定 して古い円盤星と E/T 円盤星を分離する必要がある。V > 21.5 では測光精度を 上げて、系外銀河の除去が必要である。円盤の密度則のためにはより広い領域での 観測が必要である。最後に、異なる銀系でのデータがハロー軸比の決定、 円盤のスケール高、z = 2 - 5 kpc でのメタル量の決定に必要である。これらの データは小望遠鏡に載せたCCDで採れるものである。