| 131 個のフラックス較正済みスペクトルから成る恒星スペクトルフラックス ライブラリーを提示する。太陽メタルでは、通常星の全てのスペクトル型と光度 クラス、低メタル及び高メタルでは F - K 矮星と G - K 巨星をカバーした。 各ライブラリースペクトルは異なる星の波長が重なる幾つかの観測を結合して 得られた。SIMBAD データベース、観測したカラー、ライン強度を調べて、入力 成分が似通った恒星タイプであることを確認した。 | ライブラリーの全てが 1150 - 10620 A を、半数は 25000 A までを カバーしている。赤外の欠損部は標準カラーから平滑なエネルギー分布を想定して 当てはめた。このライブラリーは将来の拡張、特に赤外での非太陽メタル量ス ペクトルの補充、を許すよう構築されている。ライブラリースペクトルは Fλ 対 λ の形で与えられている。間隔は 5 A であ る。ライブラリースペクトルを等時線上の適当な重みで組み合わせ、合成種族 の積分スペクトルを計算するプログラムを記述する。その積分スペクトルの特 徴を示す。スペクトルはテキストファイルで得ることが出来る。 |
| 多くの様々な精度と波長帯の観測を集積してスペクトルライブラリーが作ら れている。Leitherer et al 1996 にはスペクトルライブラリーの利用のレビュ ーが載っている。 モデルスペクトルは波長域と星パラメタ―の広さが特徴である。問題は細かい 吸収線を拾いつくせないことである。また、 観測と理論の間の系統的な差も問題で この点に関しては、Charlot, Worthey, Bressan 1996 のレビューがある。 | この論文では、観測スペクトルをできる限り広範に集めて、通常星のスペクトル ライブラリーを提供することである。データの欠陥も明らかにして将来の補充が 可能なように工夫した。スペクトル型の格子は Sviderskiene 1988 に従った。 これは、ベガシステム(Hayes, Latham 1975)で広範なデータを整理している。 本論文はその結果を非太陽メタル量領域に拡大したと言える。 |

|
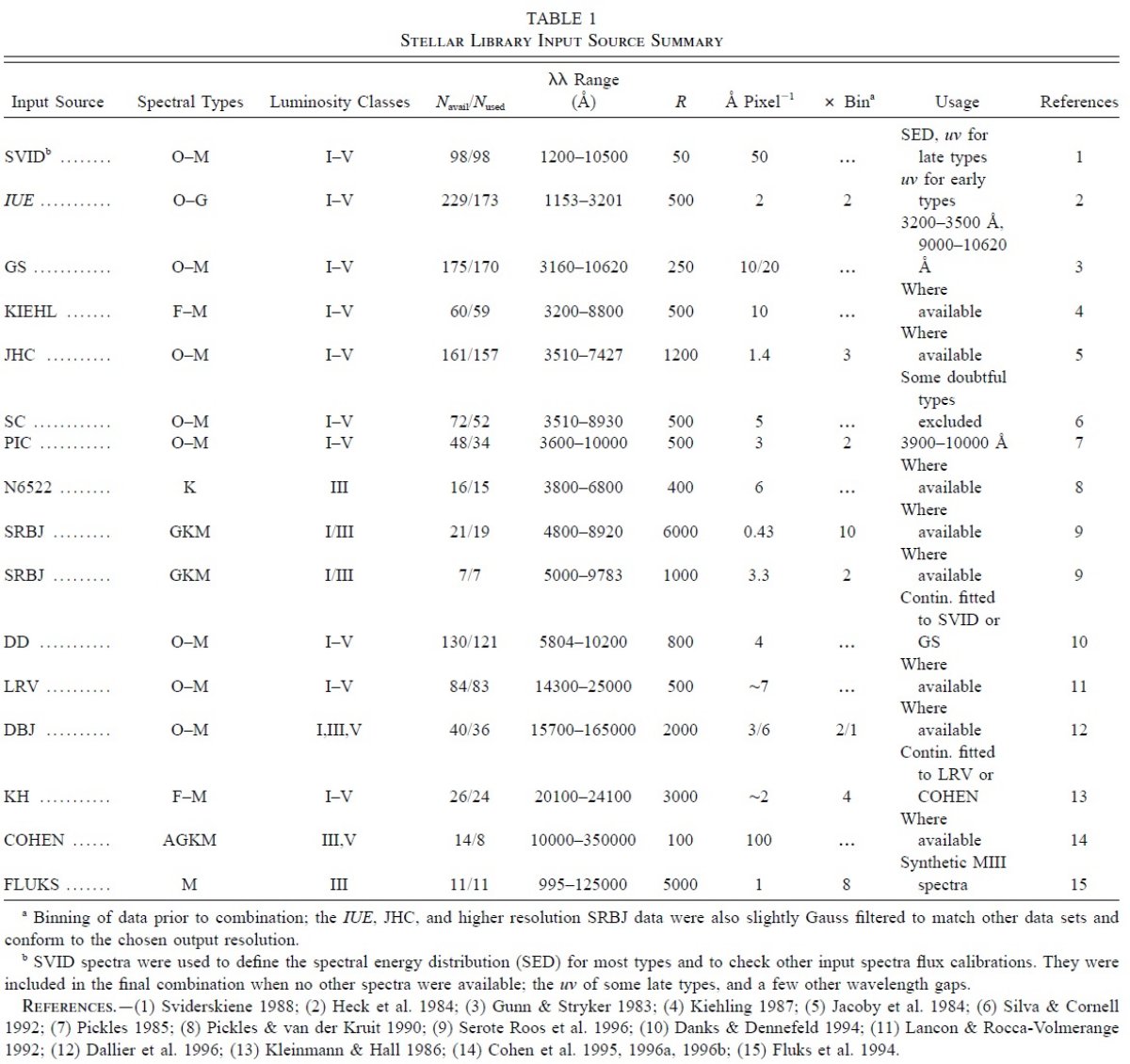
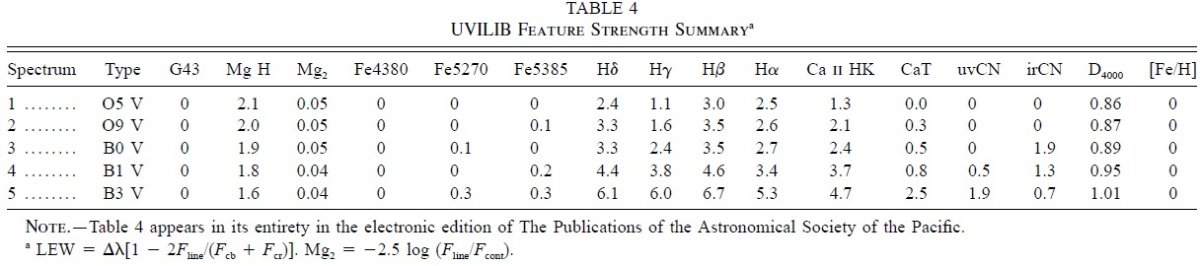
表1=データ源 表1に入力データ源名、そのスペクトル型と光度クラスの範囲、スペクトル 数と実際にここで用いられたサンプル数、波長域、分解能を示す。それらを 眺めて、全波長帯に適用可能な最高分解能スペクトルとして、波長間隔 5 A, 波長範囲 1150 - 25000 A、分解能 500 と定めた。この分解能では、 Rose 1994, Jones, Worthey 1995 が述べているような、年齢、メタル量を分離する 精密スペクトル指標の決定には不十分である。しかし、他の光度クラス、メタ ル量指標(Faber et al. 1985, Pockles, van der Kruit 1990)、それに H δ を含むバルマー線は検知できる。 |
データ合体は2段階プロセス 第1段階 紫外、可視、近赤外データから 1150 - 10620 A のライブラリーを作る。 これは UVILIB と呼ばれる。 第2段階 UVILIB データを追加の赤外データと合体させて 25000 A まで伸ばす。これを UVKLIB と呼ぶ。全体を HILIB と呼ぶ。 |
|
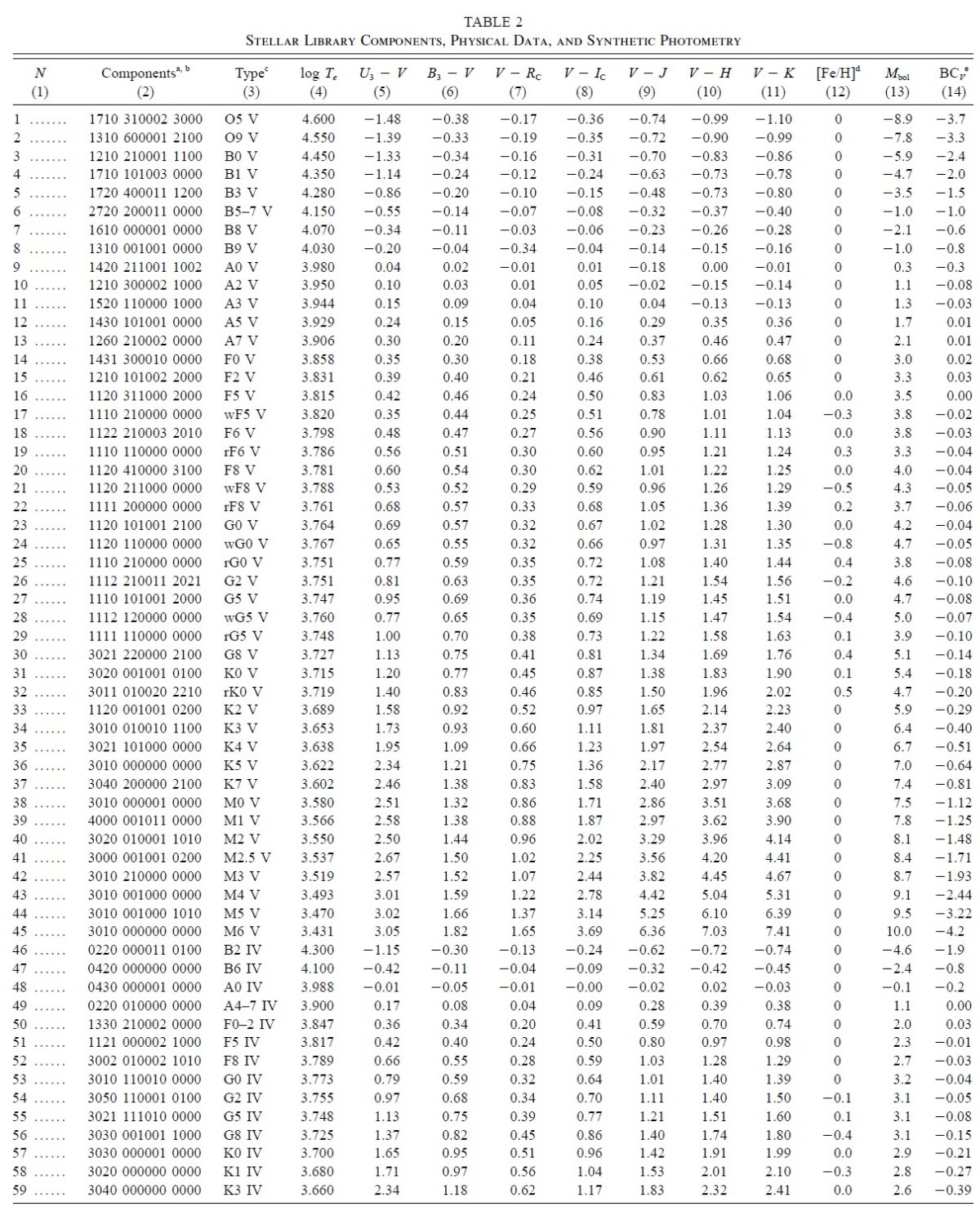
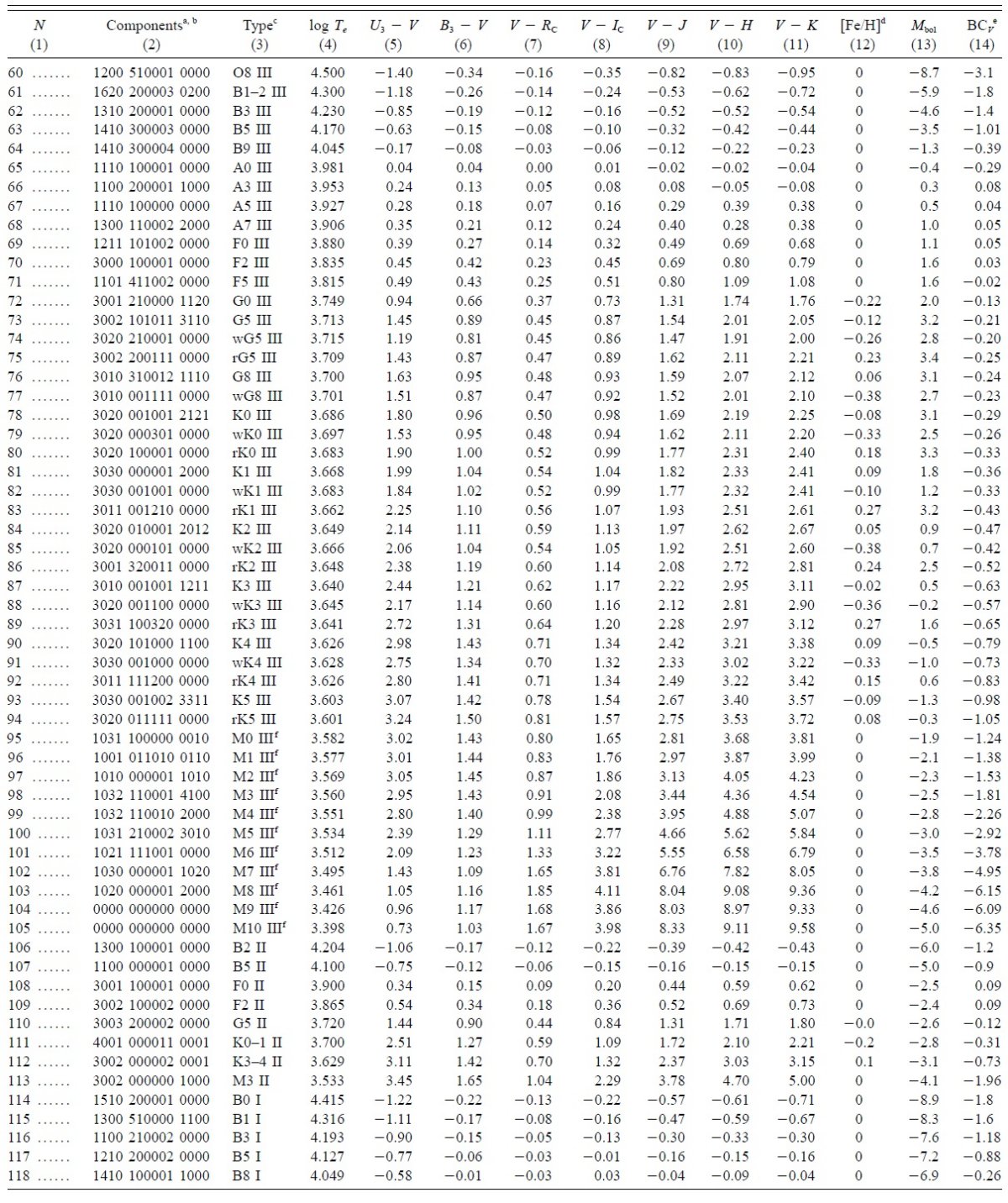
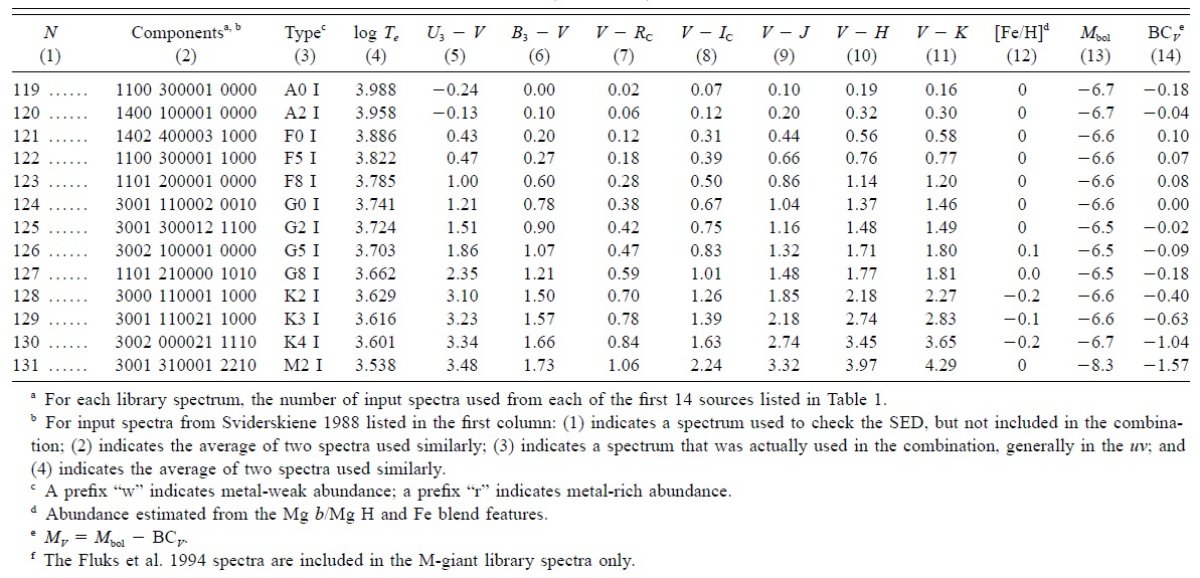
データの分類 星のスペクトル型、光度クラス、化学組成に従い、ライブラリー成分分類を 行う。SIMBAD でこの分類をチェックした。 データの調整 入力スペクトルの波長間隔、フラックス単位を統一する。波長 5556 A で フラックスを1に規格化する。SED の形が適切になるよう、滑らかな関数で 割るばあいもある。 表2=ライブラリー成分 表2にはスペクトル型、合体スペクトルに使用された観測スペクトルの数が 示されている。 |
合体作業 実際の合体作業はまず各観測スペクトルを整形して R = 500 の Fλ の形に揃え、かつ 5556 A で1に規格化する。 それらが互いに整合するかどうかを調べ、必要によっては滑らかな曲線で割り 算する。これら個々星の観測スペクトル同士から平均スペクトルを作る。 表2は最終的なライブラリースペクトルを示す。そこには、いくつの観測スペ クトルから合成されたかも示している。最大で7つのソースが使われた。 個々の観測データの星名等は長くなるので、電子データの方に記す。 実際のスペクトル合成では、まず複数のスペクトルが平均化され、その標準偏 差をが求められる。それらを3次スプライン内挿し、観測範囲外ではゼロとした こうして、1150 - 10620 A での出力形式を整える。 Sviderskiene (1988) や Gunn, Stryker 1983 の標準 SED から大きく外れたものは合体から外す。 |
3.1.SviderskieneSviderskiene (1988) の広範な SED データはこの論文の基礎となっている。 それは 1200 - 10500 A を 50 A 間隔で表す 98 本のスペクトルである。今回の 我々の目的には、波長分解能 50 は粗すぎるが、スペクトル範囲、整合性、精度 はこの論文の SED のチェックに重要であった。彼のサンプルに、低メタルと高 メタル星を追加してこの論文のサンプルが作られた。IUE データのない場合、この論文のデータを転用した。 3.2.紫外Heck et al 1984 の IUE 229星低分散スペクトルアトラスは O - F 型星 をカバーしている。これは 1153 - 3201 A を 2 A 分解能で表している。 O-型星スペクトルはダスト吸収の強さがまちまちなので、見かけの散らばり が大きい。 Sviderskiene (1988) の SED とのマッチが良い星を選んだ。3.3.可視Gunn, Stryker 1983 のアトラスGunn, Stryker 1983 のアトラスには、通常星の全スペクトル型と光度クラス をカバーして、赤化補正した 175 星スペクトルが載っている。波長は 3160 - 10620 A, 波長間隔は青で 10 A, 赤で 20 A である。 Kiehling 1987 アトラス Kiehling 1987 アトラスは F - M 型の 60 南天星 3200 - 8800 A スペクトルが 10 A 間隔で載っている。うち 11 個は低メタルまたは高メタル星であった。 Hunter, Christian 1984 ライブラリー Hunter, Christian 1984 ライブラリーは 161 の比較的高分散のスペクトル が載っている。 22 個は低メタルまたは高メタルである。波長は 3510 - 7427 A を 1.4 A 間隔でカバーしている。 |
Silva, Cornell 1992 Silva, Cornell 1992 は幾つかの研究の収集で 72 スペクトルを集めている。 波長は 3510 - 8930 A であるが、大気吸収帯はゼロにしている。 Pickles 1985 Pickles 1985 は同じスペクトル型の幾つかのスペクトルを合体させて作った ライブラリーである。48 スペクトルが含まれる。波長は 3600 - 10000 A で 間隔は 3 A である。 Pickles, van der Kruit 1990 Pickles, van der Kruit 1990 は上の幾つかを合わせて作ったライブラリー である。波長は 3800 - 6800 A である。 3.4.近赤外Serote, Boisson, Joly 1996Serote, Boisson, Joly 1996 のアトラスにはスペクトル型 G - M, 21 個の 巨星と超巨星の近赤外高分散スペクトルが載っている。その内約半数は高 メタルである。波長は 4800 - 8920 A, 間隔は 0.43 A である。アトラスには 5000 - 9783 A 間隔 3.3 A の F - M 矮星と巨星のスペクトルも含まれている。 Danks, Dennefeld 1994 Danks, Dennefeld 1994 は 126 MK 標準星を 5800 - 10200 A, 4 A 間隔で 載せた。このライブラリーは光度クラス、メタル量指標となる Na I 吸収線、 Ca II 三重線、 TiO, CN バンドが綺麗に示されている。 ただ、フラックス較正があまり良くない。 Torres-Dodgen, Weaver 1993 Torres-Dodgen, Weaver 1993 は 61 O - M 型星の 5750 - 8950 A 分光測光 データを発表した。これもフラックス較正が良くない。また低分散である。 そこで、Danks, Dennefeld 1994 を優先して使用する。ただし、 Sviderskiene 1888 と Gunn, Stryker 1983 のフラックスと合わせるように割り算を施してから合体させた。 約 30 のスペクトル型は SIMBAD の記載と異なることが判った。また、9つは メタル量が太陽でないとされた。 |
3.5.合体の精度図1は G2V スペクトルを得るためのデータと最終スペクトルを示す。 合体の際の暴れ具合は Ca II H, K 線と Ca II 3重線、 CN バンドの 周りで大きい。3.6.ライン強度局所等値巾局所等値巾(LEW) は次の式で求める。 LEW = Δλ[1-2Fline/(Fcb- Fcr)] ここに、Fline = 吸収線内の平均フラックス, Fcb = 青側連続光帯の平均フラックス, Fcr = 赤側連続光帯の平均 フラックスである。Δλ = 吸収線の巾である。それらを測定する 際の波長域は表3と4に示す。 メタル量に敏感なライン メタル量に敏感なライン Fe I ブレンド 4385, 5270, 5330 と Mb H/Mg b 5180 A が各スペクトルで測定された。それらの等値巾の和の対数を Whitford, rich 1983 の K 巨星に対して最初に行われた [Fe/H] 較正を追究した Pickles, van de Kruit 1990 の[Fe/H] 較正と比較した。メタル量評価値は 表2に載せた。 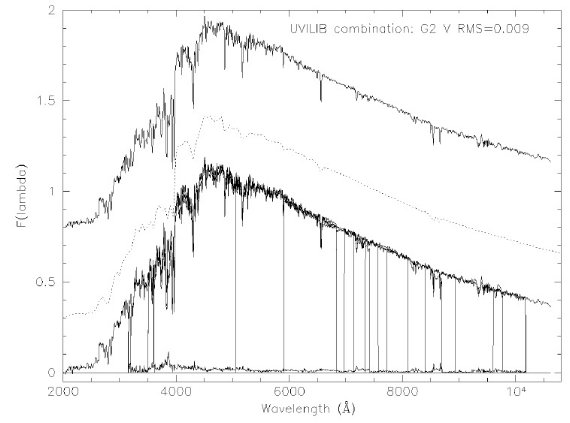 図1.G2V UVILIB 合体過程の例。表2の成分 26 に示すように、点線 = Sviderskiene 1888 を 0.3 下げて示す、を参照 SED として、 下には合体に使用した Heck et al 1984 の IUE スペクトル、Gunn, Stryker 1983 スペクトル、Kiehling 1987, Jacoby et al 1984, Silva, Cornell 1992, Serote Roos et al 1996, Danks, Dennefeld 1994 を示す。縦線は各スペクトルの端を示す。 0.8 上にシフトして示すのは最終合体スペクトルである。一番下に 標準偏差を示す。 |
この方法は早期型星に対してメタル量を低く見積もるが、
高精度でなくメタルが多いか少ないかの判定なら十分である。
図2=メタル量による変化 図2には G0V のメタル量 "w", "s", "r" に対するスペクトル例を示す。 これらはメタル量が太陽の半分、同じ、2倍を示している。 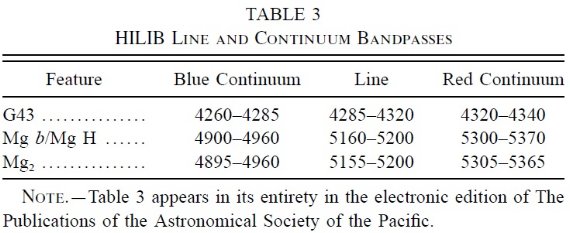 表3.HILIB ラインと連続波長域 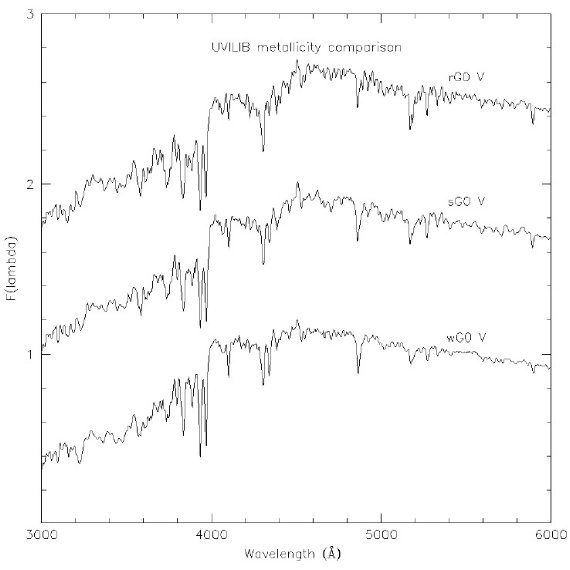 図2.UVILIB G0V スペクトルの例。上=高メタル = 2 太陽。中=太陽メタル。 下=低メタル = 0.5 太陽。メタル量が高くなると、バルマー線 Hδ 4101, Hγ 4350, Hβ4861 は弱まり、Mg H/Mg b 5175 A と Fe I (λ λ 4385, 5270, 5330) は強まって行く。 |
|
Cohen et al の絶対較正スペクトル 1.06 - 1.43 μm の区間にはデジタルスペクトルが殆どない。Cohen et al 1995, 1996a, 1996b は 1 - 1.35 μm での絶対較正連続スペクトルを 幾つかの星で公表した。その内 14 個をここで使用した。彼らの波長分解能は 低いが、絶対較正されていることのチェック価値は高い。大部分の場合、 UBVRIJHKL 測光値をスプラインフィットして連続光 SED を決めているが、 こうして決めた SED は絶対較正値と良く合っていた。 近赤外の合体 近赤外域のスペクトルデータは表2第2列の最後の4つの数字に現されている。 しかし、約半分ではそれが 0000 となっている。この場合 UVKLIB スペクトルには近赤外部の入力がなく、カラーに合う平滑な曲線しか得られない。 低メタル、高メタル星 G - K 矮星と巨星は赤外データを欠いている。デジタル データが必要である。 |
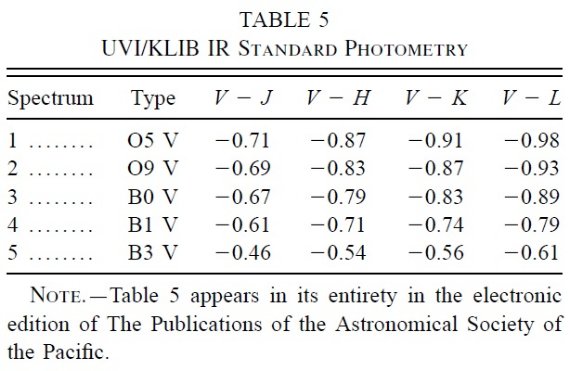 表5.UVI/KLIB IR 標準測光 |
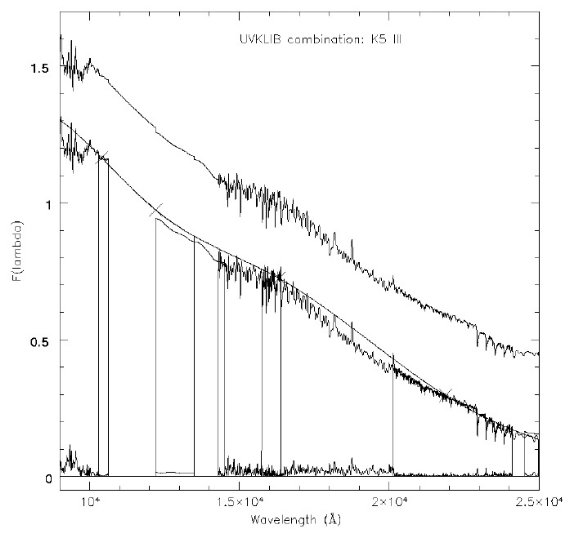 図3.K5III 星 UVKLIB 成分の合体例。Lacon, Rocca 1992, Kleinmann,Hall 1986, Cohen et al 1996a からの3つを合体。バツ印=測光を結んで平滑な 連続光スペクトルが引かれた。一番下は標準偏差。 Lancon, Rocca 1992 Lancon, Rocca 1992 のフーリエスペクトルアトラスは 84 星のスペクトル型 と光度クラスを示す。波長域は 1.43 - 2.5 μm で分解能は 500 である。 この良く較正されたデータセットのお陰で、本論文ではスペクトル波長域を 2.5 μm まで伸ばすこととなった。このデータは 1.45 μm で Cohen et al 1995, 1996a, 1996b に接続された。大気吸収も一般にはよく補正されているが、 1.9 μm 付近で水蒸気の影響が残る例もある。 Dallier, Boisson, Joly 1996 Dallier, Boisson, Joly 1996 には中分解能の H バンドスペクトルが 40 個 含まれる。波長は 15780 - 16420 A, 分解能は 3 - 6 A/pixel である。 Kleinmann, Hall 1986 Kleinmann, Hall 1986 は F - M 型、全ての光度クラスの 26 星の FTS スペクトルを含む。波長は 2.01 - 2.41 μm である。 |
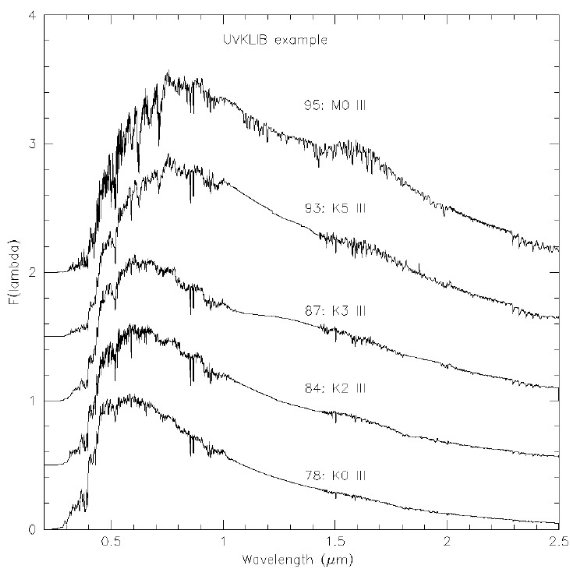 図4.UVKLIB ライブラリーの例。K 型巨星スペクトルは 10500 - 14300 A で平滑 フィットを採用しているが、 M 型巨星では Flux et al 1994 スペクトルデータが 入力されている。 Flux et al 1994 Flux et al 1994 は 380 - 900 nm の 97 個の M 巨星を観測した。その 中で最も晩期型の星は長周期変光星である。それらは数回の観測から平均 スペクトルが作られた。彼らはまた 99 - 12500 nm の範囲に亘る合成スペク トルを作成した。 UVKLIB スペクトル番号 95 - 105 では Fluks et al 1994 の M0 - M10 合成スペクトルの結果を含んでいる。合成スペクトルは吸収線強度に関し 観測スペクトルと良い一致を示すが、カラーが少し異なる。また、変光星の 平均スペクトルは他の研究でのランダムフェイズでの一回性スペクトルに 比べ、種族合成などで有利である。従って、 UVILIB スペクトルは 1150 - 10500 A では UVILIB の観測スペクトルと合成スペクトルとの 混成、それより長波長側では合成スペクトルのみとなる。 図3と図4 図3には K5 巨星の UVKLIB スペクトルの例を示す。様々な赤外成分間での 一致の良さが分かる。また図4には UVKLIB スペクトルからの 5個の 巨星スペクトルの例を示す。 1.05 μm から 1.43 μm までの つなぎに注目せよ。 |
|
有効フラックスと有効波長 フィルター "a" の透過率 Ta と等級ゼロ点 ZEROa は以下の関係で結ばれる。 ⟨Fν⟩ = Σ(Ta FνΔν)/Σ(TaΔν) Fνdν = Fλdλ, dν = c dλ /λ2 から、 ⟨Fν⟩ = Σ(Ta FλΔλ/Σ(TacΔλ/ λ2) ⟨λa⟩ = Σ(Fλ TaλΔλ)/Σ(Fλ TaΔλ) |
5.1.フィルター透過率とゼロ点可視域フィルター透過率曲線は Buser 1978 の U3 フィルター、Azusienis, Straizys 1969 から B3 と V, Rc と Ic は Bessell 1979 から得た。ゼロ点は Sviderskiene (1988) の標準スペクトルをデジタル測光して,Buser 1978 の UBV 標準星観測, Cousins 1981 の BVRI 観測カラーとの差が最小になるように決めた。 フィルター透過曲線 フィルター透過曲線は可視部を表6、赤外部を表7に示す。 |
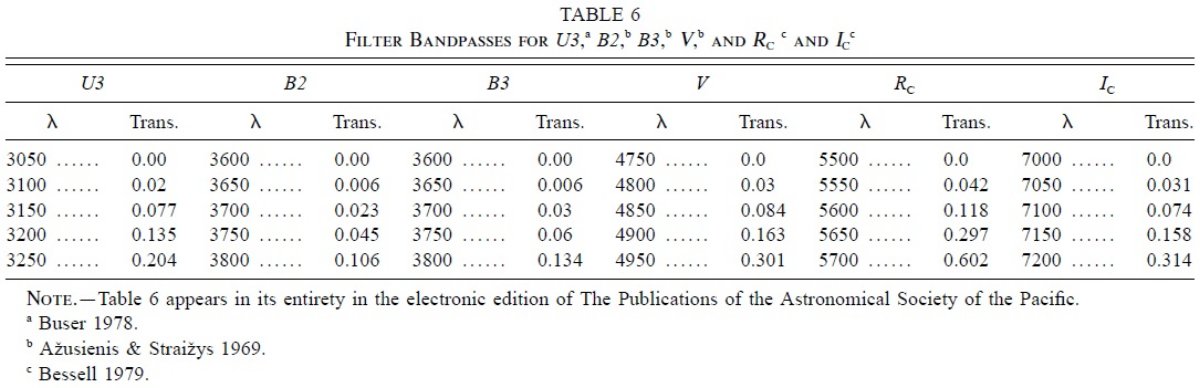
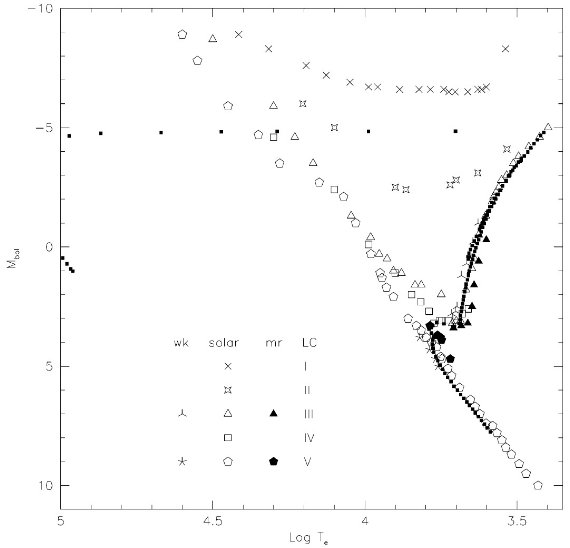 図5.黒小四角= Bertelli et al 1994 の太陽メタル、年齢の等時線。 カラー・有効温度関係 ライブラリーから計算した合成カラーは表2の第5-11列に載せてある。 表2の第4列に載っている表面温度はそのカラー V-Ic と特に V-K を Bessell 1979, Tokunaga 1997 と較べ、また M-型星では Fluks et al. (1994) を参照した。それから得られた (V-K, Teff) 較正は矮星と巨星とで大きな分離 を示す。同じ温度で較べると、M-型巨星は矮星より晩期スペクトル型となる。 これは Bertelli et al 1994 がその進化モデルで使った(カラー、Teff)関係 と大きく異なる。その影響については第7章で論ずる。 輻射補正 表2の14行に示す輻射補正は、大部分 Bessell, Wood 1984, 早期型星は Lang 1992, M−巨星は Fluks et al. (1994)、 Flux et al 1998 を参照した。与えられた恒星種族に適当なスペクトルを 構成する際に、付与された温度は各成分(表2の各行のこと)を温度光度面上に 位置づける。似たように、輻射補正はこの手続きのライブラリー各成分に対する 光度の割合を決める。表2の第13列にある輻射補正はここでは重要度が低い。 というのはそれらは選ばれた等時線に合うように調整され、ここでは Bertelli et al 1994 の太陽メタル、太陽年齢の等時線に合うように決められている からである。 ( この段落は全く意味が分からない。) |
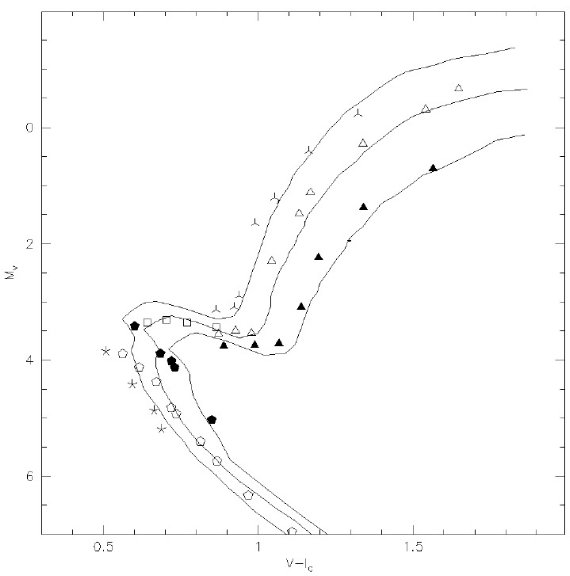 図6.Bertelli et al 1994 の太陽年齢の等時線。組成 (Z, Y) = (0.008, 0.25), (0.02, 0.28), (0.05, 0.352) モデルを (Mv, V-Ic) 図で示した。 色等級図のカバー 図5にはライブラリ点を (Mbol, log Teff) で Bertelli et al 1994 の 太陽組成、5 Gyr 等時線の上にオーバープロットした。スペクトルライブラリー からの供給で図の大部分がカバーされることがわかる。 メタル量カバー 図6は主系列ターンオフ、準巨星、早期巨星のメタル量範囲がカバーされて いることを示す。ここも Bertelli et al 1994 の半太陽、太陽、2太陽の 等時線が参考のためにひかれている。 |