|
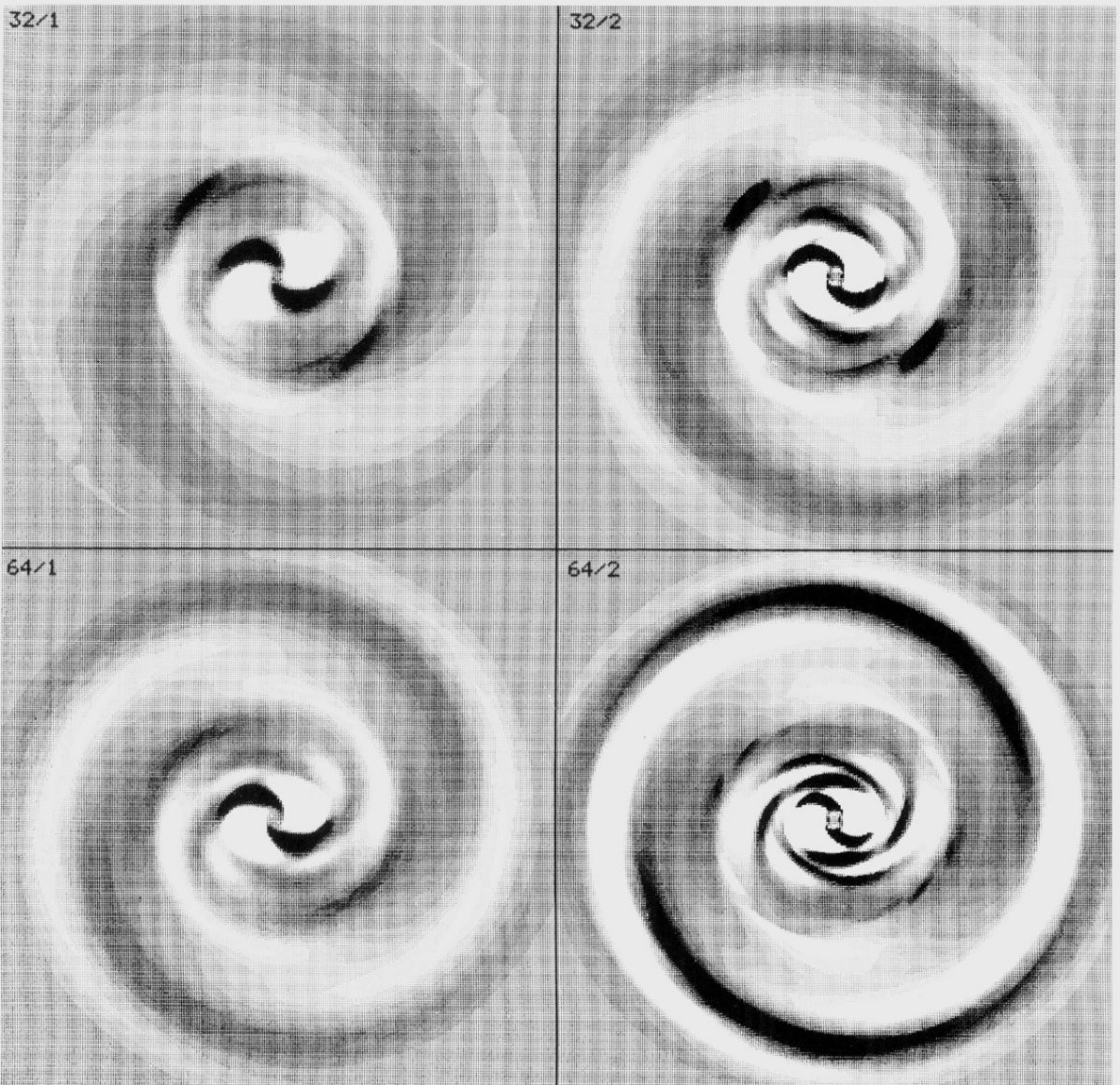
解法 ガス運動のオイラー方程式の積分を効率的に行う計算法を示す。 定常解の存在を仮定し、計算法のポイントを述べる。方程式は上流微分法で フラックスベクトル分割を通して空間を分割する。これにより衝撃波を 明快に表現できる。時間積分はインプリシット法で行われる。その形式化 で現れる線形系は多重グリッド補正法により、ガウスザイデル緩和により 解かれる。 タイプI この方法を弱いバーを含む銀河に適用した。バーの強さと、音速の 大きさに応じて、基本的に異なる二つのタイプの解が現れる。 タイプIは共回転の内側にのみ衝撃波を持つ。衝撃波でのエネルギー散逸に より内側への流入が起こる。中心密度を固定することで準平衡解が 得られる。流入率は非常に小さく、セル分割化に伴うエラー程度である。 バーとガスとの間のトルクに伴うタイムスケールは非常に長く、ハッブル 時間より大きい。流入率の小ささは一方では準平衡解の正当化に役立つが、 もう片方では実際の銀河で見られる流入量の説明には衝撃波による 散逸以外のメカニズムが必要であることを意味する。 |
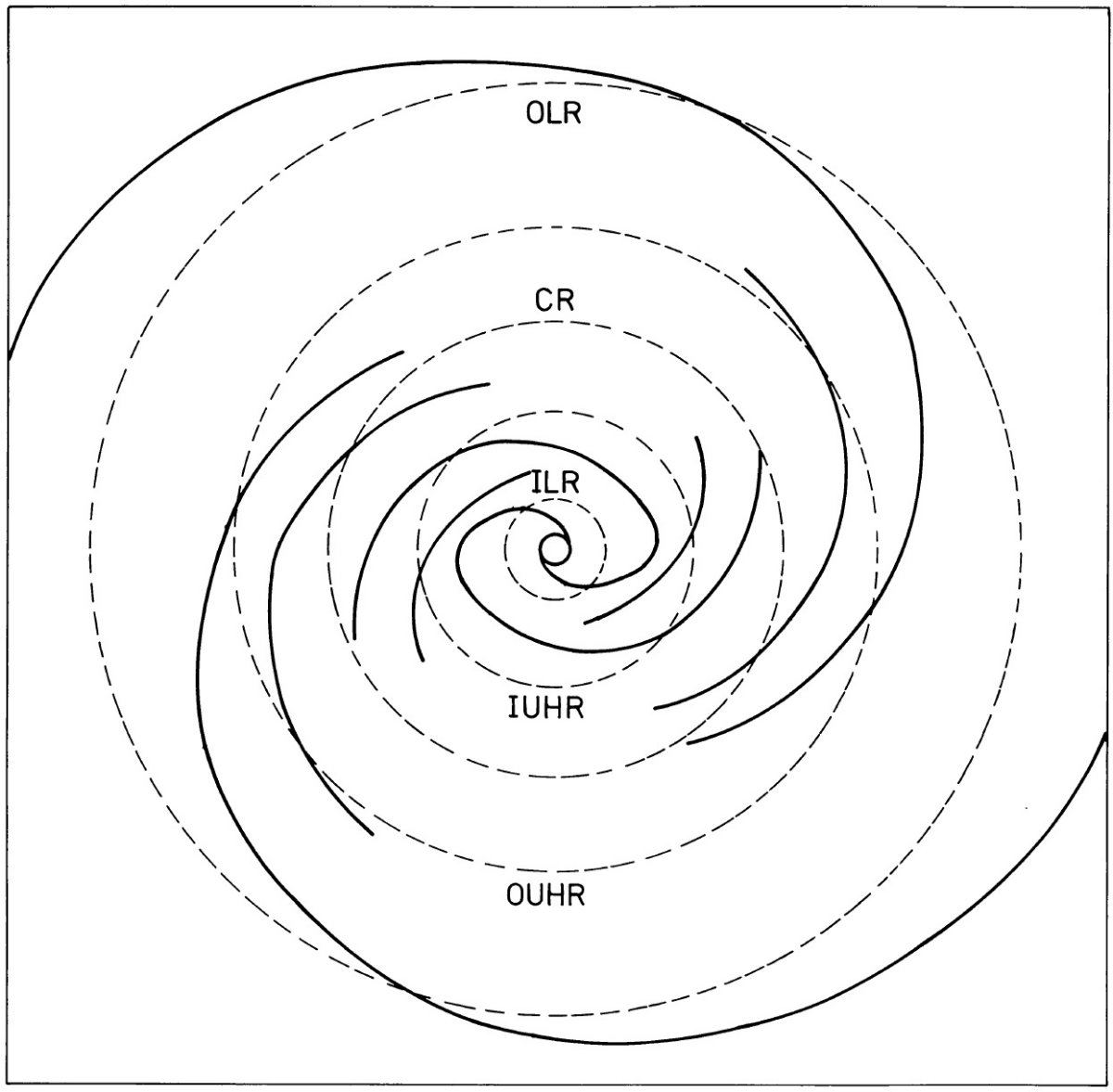
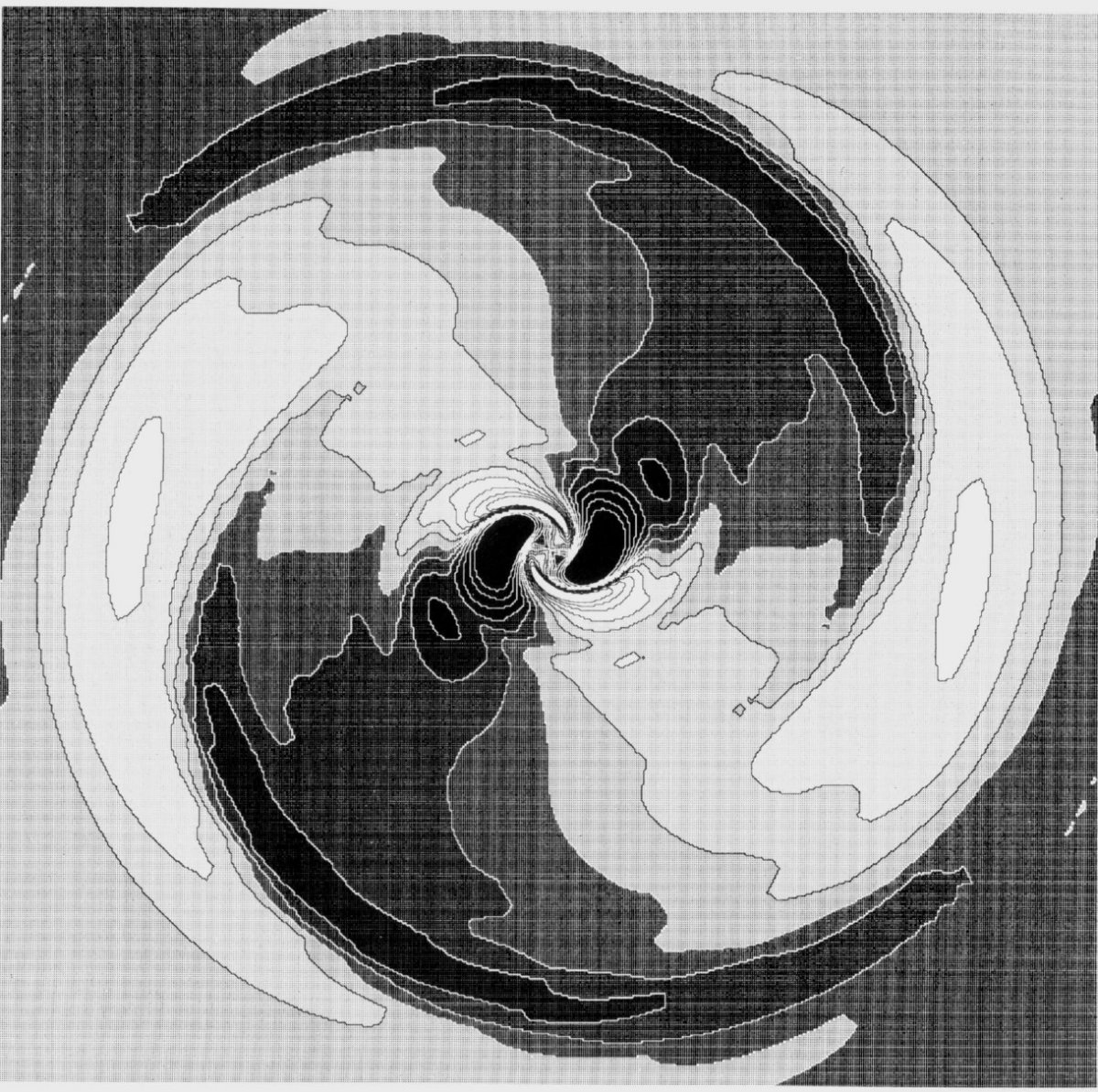
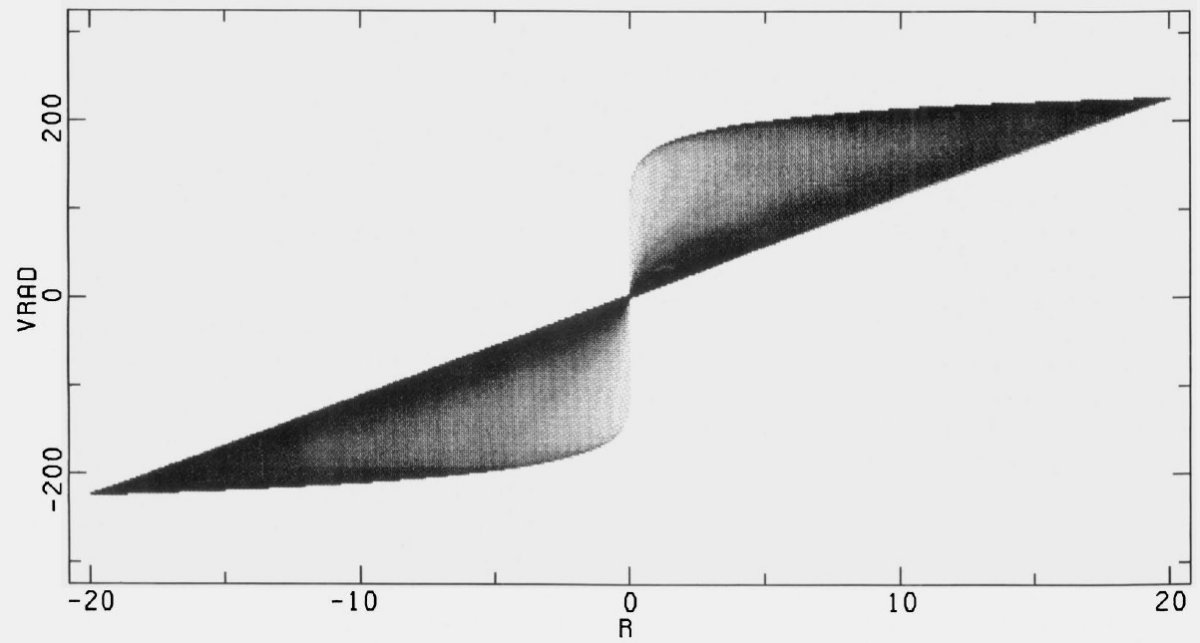
タイプII タイプIIの解は共回転の内側にも外側にも衝撃波 を持つ。内側衝撃波はガス流入を、外側衝撃波はガス流出を招く。 その結果、共回転半径の周辺からガスが消失し、二つのリングを形成する。その 一つは ILR の内部、もう一つは OLR の外側に。準平衡解を得るにはこの ガス消失領域にガスを注入し、ガスが溜まる領域から抜き出す必要がある。 回転曲線の見え方 解は強い非円運動を示す。円盤銀河の中性水素速度場に見られる傾いた リングモデルは回転楕円モデルかも知れない。真横から見た回転曲線を 幾つか示した。それらは HI 観測と較べられる。それを見ると、円運動を 仮定しての回転曲線の解釈は間違いを導く危険があると分かる。 |



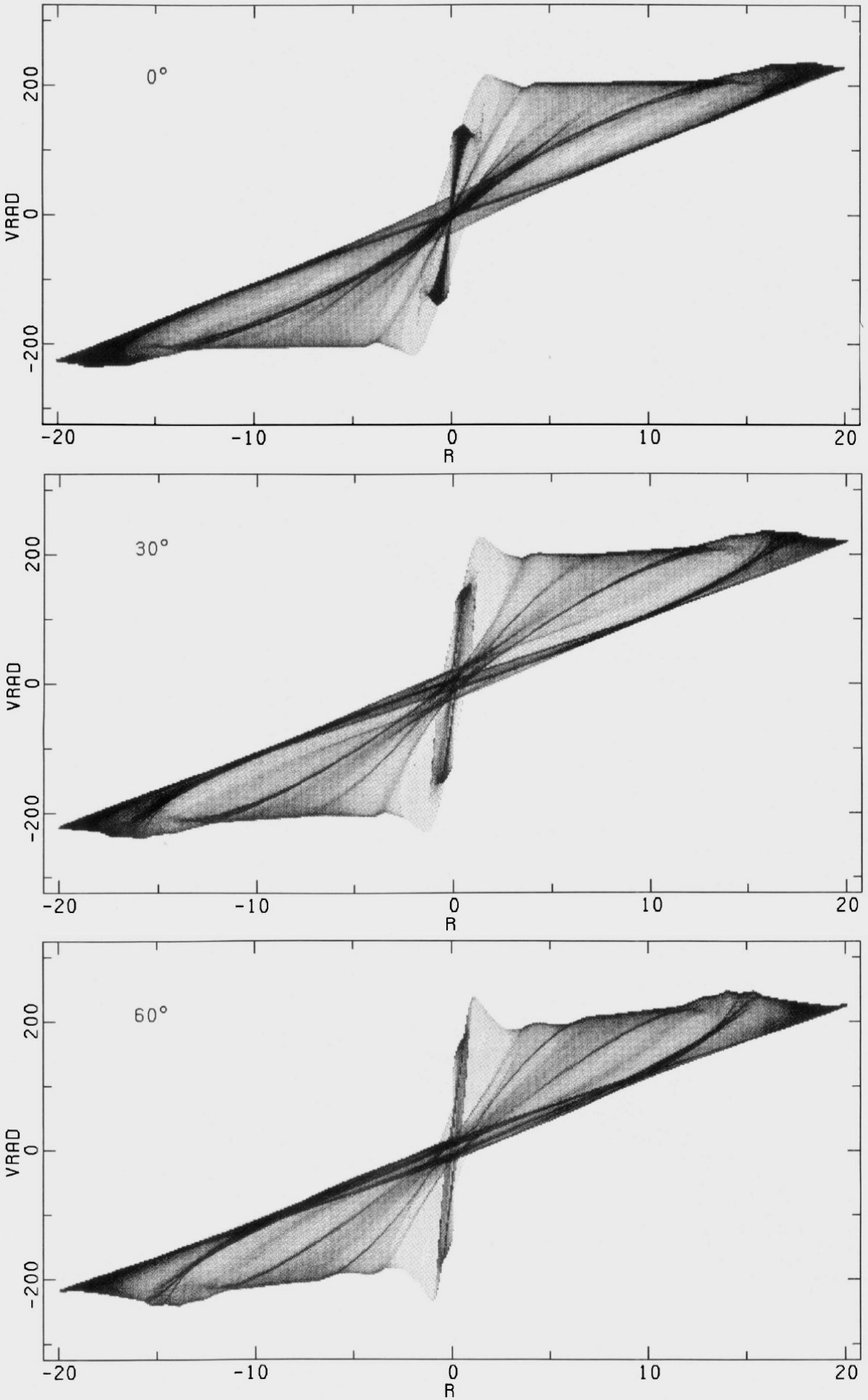
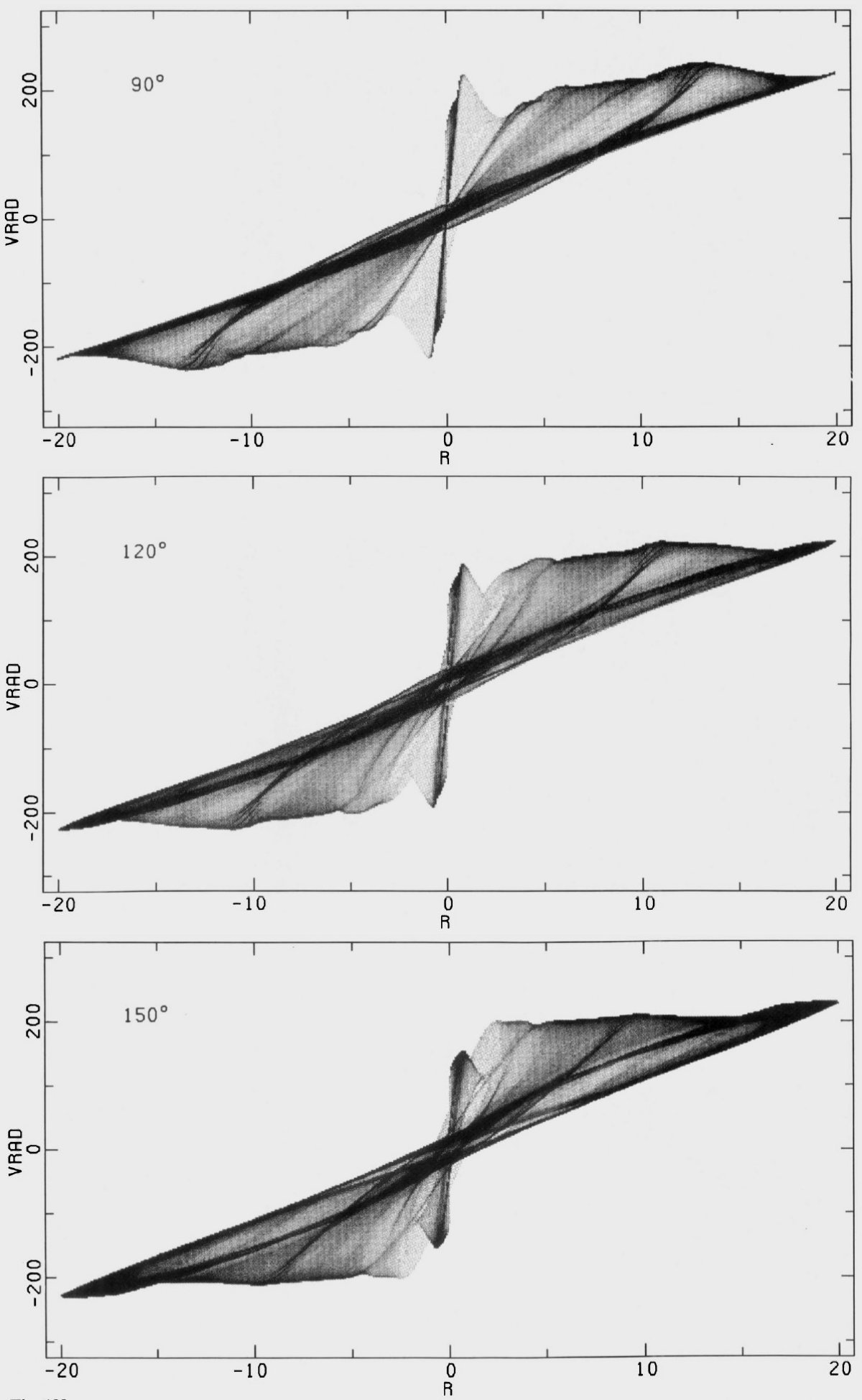



|
|
|