Age Distribution of LMC Clusters from Their Integrated UBV Colors: History of Star Formation


L.Girardi, C.Chioni, G.Bertelli, A.Bressan
Astron. Astrophys. 297, 87 - 106 (1995)



　アブストラクト　

　星団カラーカタログと等時線モデル　

　この論文では LMC 星団の年齢、メタル量、積分 UBV カラーの関係を改訂した。 Bica et al 1994 Bica et al. (1996) (BCDSP) の　UBV カラーカタログ、Bertelli et al 1994 による 単純恒星集団(SSP) の測光モデルの二つが研究の基盤である。

　測光モデルは (U-B, B-V) 面上での LMC 星団の分布、分散、それに 面上のある箇所でのギャップを良く表現した。青い星団のばあい、星の質量分布 の実現にストカスティックな効果が働くことで、カラーの分散の大部分を説明 できる。一方赤い星団では、メタル量に 0.2 dex, 色超過に 0.05 mag を付加 する必要がある。

　カラー解析の結果　

　(U-B, B-V) 面上で、積分カラーの観測値をモデルカラーと比較した結果、 以下の結論を得た。

（１）データは星団形成史にギャップが存在することに合う。LMC の年齢-メタル 関係が化学進化の単純モデルに従うなら、ギャップは 3 Gyr から (12-15) Gyr の期間に対応する。一方、もしも重元素の増加が単純モデルよりずっと緩かった ら、ギャップはもっと狭いカラー巾で起き、カラー分散のため隠されてしまう だろう。

（２）(B-V) カラーの双耳峰分布は対数年齢上ほぼ等しい割合で分布し、メタル 量が通常の AMR で決まる星団の連なりによって再現される。 （ギャップは？）　ある年齢で星団の積分カラーに「相転移」 が生じる (Renzini,Buzzoni 1986) という仮説は必要が無い。


（３） Bica et al. (1996) が発見したギャップは, (U-B, B-V) 面上でカラー特別な 方向に分散することで説明される。星団の積分特性が突然変化すると考える 必要はない。

　カラーから年齢へ　

　この解析の結果は、 Elson, Fall (1985) (EF85) による星団の積分 UBV カラー に年齢を当てはめるという経験的手法を改訂することに使われた。 EF85 法は 低メタル星団に対し、年齢とカラーの間の正しい関係を与えない。したがって、 古い星団の年齢を決めることが出来ない。我々は EF85 に出てくるパラメターＳ の定義に修正を加え、赤い星団の年齢系列が正しく記述されるようにした。 そして、カラーを分散させる様々な効果による年齢誤差を最小にした。 年齢系列は 24 個の標準星団により年齢を較正された。標準星団の年齢は 最新のＣＭＤから導かれている。

　年齢分布関数の特徴　

最後に、我々は BCDSP カタログの全ての星団に年齢を付与した。そして、LMC 星団の年齢分布関数 (ADF) を作った。新しい ADF はこれまでの UBV 解析では 出て来なかった新しい特徴を明らかにした。それは、星形成の活発な時期が ≈ 100 Myr, 1-2 Gyr にあり、3 - (12-15) Gyr のギャップの存在である。 (B-V) カラー分布に現れる　2 つのピークはこれら星形成高潮期がいつであった かに敏感である。極端に赤い星団の欠如は、中間年齢と古い星団の間にギャップ が存在することを示唆する。

　1.イントロ　

　マゼラン雲星団の意義　

　マゼラン雲星団は、銀河の恒星種族研究のテンプレートとして、恒星進化 の較正材料として多くの研究がなされてきた。これら星団がそんなに貴重な理由は 若い星団のメタル量に巾がある、と共に星団が比較的大きいからである。

　星団の積分測光とこれまでの研究　

　最近まで、星団の大規模サンプルは積分測光の形でしか得られなかった。

初期の積分カラーサーベイ
　 Searle, Wilkinso, Bagnuolo (1980) 　　Q(ugr)-Q(vgr)図上で SWB 系列を示す。
　Frenk and Fall 1982　"equivalent(E-)" SWB 系列を (U-B):(B-V) で示す。
積分等級カタログ
　 van den Bergh (1981) 積分UBVカラーカタログ＝数ソースからの寄せ集め
　　　 Elson, Fall (1985), Chiosi et al 1988　　UBV カラーと(年齢、メタル）の関係、ADF
　Bica et al 1991, 1994（BCDSP) 数が４倍に増え、CCDで一様なデータ

　データは増えたが、問題はメタル量。同じ星団のメタル量が、研究毎に全く異 なる値になる例は多い。多くのサンプルに一様な方法でメタル量を与えた例は 最近の Olszewski et al 1991 のみである。

　本論文の研究方法　

　Girardi,Bica 1993　Bicaデータの予備的解析（太陽組成のケース）
　　――＞総カラーにストカスティックな効果が大、ADF決定にIMF勾配が重要

この論文では新しいモデルでSSPの年齢、メタル、カラー関係を調べた。
　１．新しいアイソクロン(Bertelli et al 1994)採用.
　２．Bica データ
　３．AMR,　UBVカラー分散の原因＝
　　　　　　　　　　質量分布のストカスティック効果、赤化を注意
　４．積分カラーから年齢を求める方法を直した。
　　　(a) 最新CCDデータでCMD――＞しっかりした年齢基準
　　　(b)　 Elson, Fall (1985) のUBVカラーーー＞年齢法を改善
　５．LMCクラスターの年齢分布＝２つのバースト

　２．星団の理論的積分カラー


　２．１．SSP の測光進化　


　モデルの準備　

進化モデル＝　Bressan et al 1993, Fagotto et al 1994
アイソクロン＝　Bertelli 1994
SSP 積分カラーの手法＝　Alongi/Chiosi 1989, Gitatdi/Bica 1993
SSP IMF = φ ∝ m-(x+1) (x=1.35)

　Z = 0.02 SSP モデルのカラー変化　

　下図１にメタル毎にSSPのUBVカラー進化を示す。二色図はlogt=0.1の巾で平滑化 されている。
Z=0.02を例に図１を説明すると、

１）logt=7付近で赤色超巨星が出現する。そのため、赤いループを描く。その後



図１．メタル量の異なる SSP 積分カラー の時間変化。メタル増加モデル A と
　　　B のカラー年齢関係（log t > 9）も示す。若いモデルは Z=0.008と同じ
　　　(a) = (U-B)o, (b) = (B-V)o

のカラーは赤色超巨星と青色超巨星のバランスで決まり、図２の二色図上では、 (U-B)=-0.7, (B-V)=0.1付近でループを描く。

２）Girardi/Bica1993であったlogt=8付近で赤くなる現象は今回起こらない。９３ 年ではヘリウム燃焼期間と水素燃焼期間の比がt(He)/t(H)=0.25 だったが、現在の モデルでは0.1 と小さいためである。観測との一致は向上した。

Z = 0.02 に限って言うと、以下の二つの特徴が目につく。 ３）(U-B):(B-V)図上でlogtの刻みがほぼ等間隔になる。　年齢推定に重要。

４）二色図上(B-V)=0.3(logt=8.7)，0.7(logt=9.2) で傾きが変化。　LMCのB-V 分布の双耳峰に関係。

１）は Elson, Fall (1985) で最初に導入されたパラメター S と年齢の関係の基礎となる。
２）は (B-V) 分布の双耳峰性に関して重要な意味を持つ。強調しておきたいこと は、モデルには全ての進化段階が含まれるが、星団積分カラーの決定要因は 上部主系列星と中心 He 燃焼 (CHeB) 期星のカラー進化である。


図２．異なるメタル量 SSP の (U-B) - (B-V) 進化。目盛りはΔlog t = 0.1


　低メタル SSP のカラー進化　

　低メタルになると SSP 進化はどう変わるだろうか？

　若い低メタル SSP

若いと、 logt=7の超巨星効果は弱くなり、logt=8でのAGB出現によるB-Vの赤化が目立つ。 ただし、若くて低メタルはないのでこの効果は観測されない。

ただし、SMCを見ると、 Elson, Fall (1985) が言っていたように、

１）(U-B) < -0.4 SMCはLMCよりB-Vが0.15青い。

２）-0.4 < (U-B) < 0 SMCはLMCよりB-Vが0.1赤い。

で　Z=0.001, 0.004 の傾向に合っている。



　古い低メタル SSP

古いと右下の赤い領域拡大図に示すように、古い（t＝１５Ｇｙｒ）星団では 低メタルになると (U-B) も (B-V) も青くなっていく。

３図で太線はRacine による銀河系球状星団。図の線をそれに合わせるため、 (U-B) を 0.03,　(B-V) を -0.05 ずらした。　



図３のマーク付きの実線は下側が丸でモデルＡ，上が四角 でモデルＢ．年齢が古くなると上（青）に上がって行く。

図３．図２の赤い部分を拡大。モデル A, B は log t > 9.1 のみ表示。
　　　若いと Z = 0.008 SSP のラインに重なるからである。
　　　カラーのゼロ点を Δ(B-V) = -0.05, Δ(U-B) = +0.03 ずらし 、銀河系
　　　球状星団のカラー系列(Racine 1976)を再現するようにした。
　　　メタルが既知の球状星団を四角で示した。メタル量 [Fe/H] は,
　　　-0.71(47 Tuc), -1.40(NGC288), -1.29(NGC1851), -1.69(M79)
　　　-2.24(M92), -2.13(NGC7099) (Djorgovski, Meylan 1993)



　３．LMC の簡単な化学進化モデル　


　二つの年齢-メタル量関係 (AMR) の仮定　

古い星団は低メタルで、そのため古くなると星団系列は (U-B) - (B-V) 面上で フックを描く。これをはっきり示すため、次のような簡単な AMR を仮定した。

モデルA（右）　　　Z=0.008(1-t/15Gyr)
　　　　　　　　　　　　Searle/Sargent 1972の単純なモデルに対応

モデルB（左）　　　[Fe/H]=-0.4-1.6(t/15Gyr)
　　　　　　　　　　　　　Z = 0.02 × 10-0.4 × 10 -1.6 (t/15Gyr)
　　　　　　　　　　　　初期のメタル増加はより緩やか。

モデルＡは Z が時間にリニアに、モデルＢでは log Z が時間にリニアに変化する。 どちらも t = 0 では Z = 0.008 ([Fe/H]=-0.4) となる。ただし、t = 15 Gyr では 差が出る。モデルＡでは Z = 0 となるが、モデルＢでは [Fe/H] = -2 である。

どちらも LMC の観測的な AMR:Olszewski et al 1991 AJ 101,515 と合うことを 注意しておく。3 - 12 Gyr サンプルなし期間のため、そこでの AMR が定まらな いのである。古い Cohen 1982, Smith et al. 1988 では年齢推定がラフであった ため。却ってその不定性は現れなかったのである。




図４． Bica et al. (1996) データによる観測２色図。図２の SSP 進化ラインを重ねた。
　　　前景赤化 E(B-V) = 0.07 を足してある。丸の大きさは明るさを示す。 		　SSP カラーへの補正　

SSP のカラー進化を図３でプロットする際にカラーに以下の補正を施した。

　　　　　Δ(B-V) = -0.05,
　　　　　Δ(U-B) = +0.03

この補正は、Z = 0.004 log t = 10.2 SSP のカラーが 47 Tuc ([Fe/H]= -0.71)の カラー、(B-V)o = 0.84, (U-B)o = 0.34, Djorgovski,Meylan 1993 と一致させる ためである。この補正により、古い SSP と銀河系球状星団のカラー (Racine 1976) は全メタル量に対して完全に一致するようになった。それは、図３上の白丸、 [Fe/H] = -0.71 (47 Tuc) から [Fe/H] = -2.2 (M 92) までで明らかである。

カラーの補正が必要だった理由を探るため、SSP モデルに次の変光を加えた。
（１）IMF を x = 1.35 から x = 0 まで変える。
　　　　　カラーは 0.02 までしか変化しない。
（２）マスロスパラメター η を 0.35 から 1.0 に増やす。
　　　　　カラーは 0.03 しか変わらない。それも Z = 0.0004 の時のみ。

どちらも説明できず、モデルから等級、カラーへ移る際の変換が原因かもしれ ない。以下では SSP カラーを観測と比較する際にのみ上の補正を施す。

観測とモデルのカラー比較　　

　図４は様々なメタル量 SSP のカラー進化を示す。比較のため、BCDSP データ も重ねた。全体の一致、特に明るい星団に対して、はよい。古い星団が、 Z < 0.004 なことは確かだ。さもないとずっと赤くなるだろうから。観測点の 分散の原因は第４章で論じる。

　５図は４図の赤い領域の詳細である。＊はRGB星出現 log t = 9.05 を示す。 モデル A (右）も B（左）もフック（ SWB の V, VI. VII)を再現している。 ただ、B が観測分布の真ん中を走っているのに対し、A はちょっと赤い方へ つんのめりすぎ。これは 5.2.節で論じる。空白帯は Bica による不作帯


図５．図４の赤い部分を拡大。本文で論じたカラーゼロ点のシフト加算済み。
　　　さらにアステリスクで SSP に RGB が現れる点(log t ≈ 9.05) を 示した。
　　　実線の帯は Bica et al 1991 の分布に現れるギャップ。モデルA,B も。


　４．カラーが分散する原因　


　４．１．ストカスティック効果　


　ストカスティック効果：これまでの研究　

　Chiosi,Bertelli,Bressan 1988 と Girardi,Bica 1993 は、現実の星団において IMF へのストカスティックな影響による分散量を評価した。彼らはいくつかの 点に注意を喚起した。

（１）　若い星団では、ストカスティックな影響により積分カラーに大きな分散
　　　　が生じる。特に赤色超巨星期の分散が大きい。

（２）　分散の大きさは時間と共に変動する。

（３）　分散の方向は赤化の方向と似ている。

（４）　BCDSP 星団のように低光度の場合、積分カラーの解釈にはストカス
　　　　ティックな効果を考慮すべきである。

　数値実験の手順　

　この問題を調べるため、年齢、メタル量、Ｖ等級 を固定した星団モデルを多数 計算して、その積分カラーの分散を調べた。やり方は CBB88, GB93 と同じである。

　（１）決めた年齢の SSP に対し、IMFを出現確率関数と考えて、モデル星団
　　　　に属する星を選んで行く。

　（２）星団の絶対等級が Mv = -6 になるまで星を足して行く。

　（３）そこでカラーを計算する。

　（４）この計算を各年齢で５０回繰り返す。

　（５）σ(B-V)=⟨|B-V-⟨B-V⟩|⟩, σ(U-B)= ⟨|U-B-⟨U-B⟩|⟩ を年齢に
　　　　沿って計算する。

Mv = -6 は、BCDSP サンプルが V = 13 まで載せているからである。
ストッカスティック効果はMvによると思うが。或る星団マス で出発して、年齢とともにマスが減少して行く。出発マスもある分布で与えるとい うのが正しいと思う。それで結果がどう変わるかは？

　数値実験の結果　

計算結果を図６に示す。主な内容は、

log t < 6.8　　　　　赤い星なし。上部主系列(カラー一定)で決まる。分散小
6.8 < logt < 7.4　　 分散　大。　赤色超巨星が何個出現するかどうか。
7.4 < log t 　　　　年齢と共に多数の後主系列星が出現し、分散は急低下。
　　　　　　　　　　　8.2 < log t では分散方向はΔ(U-B)/Δ(B-V)=0.45
9.1 < log t 　　　　RGB星出現で分散低下。分散方向はΔ(U-B)/Δ(B-V)=0.9

　Mv が変わると、カラー分散がどう変わるかについては以下の関係がある。

　　　　　σ(B-V) = σ(B-V)Mv=-6×0.7(Mv+6)

この式の適用範囲は -5 > Mv > -9 である。この式はσ(U-B) にも当てはまる。

　数値実験の結果　

　低メタルの場合にも計算を実行して類似の結果を得た。大きな違いは、若い SSP で赤色超巨星が発達しないため分散が小さいという点である。


図６．ストカスティック効果による平均カラーからの分散。σ(B-V), σ(U-B)
　　　 クロス＋実線は Z = 0.008, Mv = -6 モデル。
　　　　点線はメタル量を ± 0.2dex 変化させた時のカラーの差。
　　　　最下段は、分散の方向の傾きを示す。


　４．２．カラー分散の他の要因　


　同年齢の星団間のメタル量の分散　　

　Olszewski et al 1991 の若い、および中間年齢星団を見ると、メタル量が [Fe/H] = 0 ±0.2 から [Fe/H] = -0.7 ±0.2 まで拡がっている。 これは星団間の固有の分散が σ([Fe/H]) ∼ 0.2dex あることを示唆 する。Frogel et al 1990 も 年齢 ∼ 1 Gyr 星団内部の赤色巨星の カラー分散から類似の値を得ている。

　メタル量分散が星団積分カラーに及ぼす影響は、異なるメタル量の SSP で カラーを計算すればすぐ分かる。それは、図６で Z = 0.008 の周りに メタル量を 0.2dex 変えた場合のカラー変化として点線で示されている。

　　　　　同年齢の星団間のメタル量の分散
log t < 8.0　　　　　メタル量分散の効果はほとんどない。
8.4 < logt 　　　　　 (U-B) でメタル分散効果がストカスティックを上回る。
8.8 < log t 　　　　　(B-V) でメタル分散効果がストカスティックを上回る。

　この結果、(U-B)-(B-V) 図上赤い部分で分散の平均勾配は幾分急になる。

　赤化の分散　

　Persson et al 1983 による E(B-V) データは LMC 全体で σ[E(B-V)] ≈ 0.05 の分散があることを示す。これは、これは年齢が log t > 8.5 の星団に


対してカラー分散を生じる。赤化ベクトルの勾配は Δ(U-B)/Δ(B-V) = 0.72 である。

　測光エラー　

　Bica et al 1992 の図２は BCDSP データの内部測光エラーは V = 13 で 0.05 mag 以下であることを示す。V = 12 より明るくなると、測光エラーは無視できる 程度に下がる。

　他の不定性要因はフィールド星混入である。大部分の星団に対しこの影響は 小さいが、背景が非一様な箇所では効いてくる。しかしこの効果の評価は難しい。 したがって、測光エラーが効いてくるのは暗い (V ≥ 13) 星団で年齢が log t ≥ 8.0 の場合である。

　カラー分散効果のまとめ　

　以上の議論から以下が明らかになった。

　　（１）ストカスティック効果は若い星団で支配的である。

　　（２）赤化＋メタル量効果は log t ≥ 8.5 で効く。

　５．データ解析　


　BCDSP カタログの説明　

　カタログは ESO/SERC プレートから一つづつ選ばれた 624 天体を含む。 サンプルは V = 13.2 まで完全である。カタログには HIIR 内の恒星集団 が 100 以上含まれている。それらの多くは明確に星団とは分類しがたい。 つまり、重力的に束縛されているかどうか不明である。その上、ガス放射光 が恒星成分の UBV カラーの測定を困難にしている。幸運なことにそれらの 大部分は (U-B, B-V) 面上特定の領域に集中している。実際のところ、 それらが存在するのは、BCDSP の E-SWB クラス 0 領域（B-V < 0, U-B ≤ -0.7）である。我々はこれらの星団をリストに含むが、 それらの UBV カラーの解釈には注意が必要である。

　５．１．二色図の解析：カラー分散の影響(モデル)


　図７には何がプロットされているか　

　BCDSPデータとSSPカーブは２色図上で大局的にはよい一致を示す。より細かい 比較には LMC メタル増加史とカラー分散の双方を検討する必要がある。

　このために、図７にはモデルＡとＢについて、（１）メタル増加を組み入れた 平均カラー進化に、（２）ストカスティック効果をシミュレートするモデル星団のカラー 分散を載せた結果を示した。シミュレーションは Δ log t = 0.1 毎に　 50 モデル星団を使って計算された。log t < 8.0 では Mv = -7, log t > 8.0 では Mv = -6 とした。Mv のこの年齢依存は BCDSP で示された年齢と共に 等級が上がって行く傾向を表したものである。

　これに加え、図７ではメタル量を ±0.3dex 変えたモデルによるカラー 変化もプロットした。それらは同年齢星団間のメタル量の分散によるカラー分散 の巾を示している。

　平均分散ベクター　

図７を見ると、メタル増加の効果と、ストカスティック効果とメタル量分散によ るカラーの広がりの双方が示されている。図中には log t = 8, 9 での カラー分散の方向を矢印で示した。この方向を平均分散ベクターと呼ぼう。

　若い星団　

B-V < 0.4 の若い星団のデータ散らばりはストカスティク効果で説明でき そうである。図４と図７を比較せよ。

非常に若い星団は、B-V = -0.1 より青い集団と 0.7 付近まで伸びる集団 の２グループに分かれる。これは一個か２個の超巨星が現れるか どうかで、Mv = -7 星団のカラーが大きく変化するためである。

図７のシミュレーションは図４と較べるとこの効果を過大に扱っているらしい。 しかし、非常に若い星団の大部分は Mv = -7 よりずっと明るいので、実際には この効果は緩和されるのである。

　古い星団　

赤い星団の２色図上での分布を決めるのはメタル増加史である。
あんまりよく分からない
ストカスティック効果は分散の説明には不十分で、赤化の分散やメタル量 分散が必要であろう。




図７.(a) 実線＝モデルＡ(Ｚ増加率が一定)とその両側メタル量が ±0.3dex の カラー進化。Δlog t = 0.1 毎に IMF のストカスティク効果の 50 シミュ レーション結果をプロットした。
影付きの矢印は、log t = 8 と 9 での全ての効果を合計したカラー分散の方向 を示す。実線の箱は BCDSP で見つかったギャップを示す。箱上部が星団不在な ことに注目せよ。
　　(b) モデルＢ([Fe/H] 増加率一定)の場合。


　５．２．年齢ギャップの証拠は本当にあるのか？


　星団年齢とメタルが２グループに分かれる。　

Olszewski et al(1991)： クラスターの年齢とメタル分布に二つのピークがある。

　E-SWB = I-VI　　0.0>[Fe/H]>-0.7　　若い、中間年齢　(数Myr<t<3Gyr)
　E-SWB = VII　　-1.7>[Fe/H]>-2.2　　古い（１２Gyr < t)

ESO121SC03を唯一の例外として３−１２Gyrの星団はない。(DaCosta 1991)

 　(U-B, B-V) 面上にギャップが現れるのか？　

図５でこのギャップが二色図上の分布に反映されているかどうか調べた。

モデルA ギャップは B-V > 0.8 に対応。確かにそこには星団がない。
　　　　　ギャップは星団の観測分布と矛盾しない。様々なカラー分散過程が
　　　　　モデルＡの経路をぼやかすことを考慮するとこれはより真実になる。

モデルB 観測分布の中央を通る。これは観測されるギャップと矛盾する。
　　　　　しかし、3 < t < 12 Gyr の年齢はモデル B では B-V ∼ 0.77,
　　　　　0.12 < U-B < 0.21 に対応し、そこは非常に古い星団の占める領域
　　　　　 (U-B) ≤ 0.18 と部分的に重なる。したがって、年齢ギャップの巾は
　　　　　 Δ(U-B) = 0.03 となり、検知が非常に困難となる。また、この年齢
　　　　　ギャップも (U-B) - (B-V) 面上の観測点分布と大きくは異ならない。
モデルＢは検知困難だが位置は正しいということか？

５．３．(B-V) カラーにおける van den Bergh ギャップ


　(B-V) ギャップ　

Van den Bergh (1981) はB-V = 0.5 を中央に、巾 0.3 のカラーギャップを指摘 した。

その後の研究は、

１）フェイズトランジション　(Renzini,Buzzoni 1986)
　　SSP に RGB, AGB が初めて出現する際のカラー急変。
　　Bressan1994 のモデル研究によると、そのような変化は起こらない。

2) ブルーループ　(Battinelli/Capuzzo-Dalzzetta 1989)
　　CHeB星のブルーループが古いSSPほど赤い側に移行し、ついにはある年齢
　　でハヤシライン近くのRCへと合体する。この現象がRGB出現フェイズトラン
　　ジションと一緒にギャップを生む。
　　B-V=0.4でCHeB星があるNGC1831, 1868, 2249 の存在と矛盾する。

３）カラーの縮退　(Frenk/Fall　1982)
　　ギャップの原因をカラーの縮退に求める。ギャップより青いクラスターは
　　B-V の範囲が狭いためにかたまる。ギャップより赤いのは中間年齢でメタル
　　高と、老齢で低メタルは似たカラーを持つ。このため、進化系列上同じ割合
　　にばら撒かれてもカラーは双ピークになる。

４）年齢―メタル関係と星の年齢分布　CBB88
　　年齢―メタル関係 (AMR) によりギャップの位置が決まり、星の年齢分布
　　(ADF) で赤と青の比率が決まる。

　BCDSP サンプルに見るギャップ　

図８を見ると、ギャップはvan den Bergh が言うほどはっきりしない。
主な理由の１つはBCDSPサンプルが小さいクラスターまで含み、それらの新しい データがギャップを埋めてしまうからである。それに関連して、図８では (B - V) > 0.4, (U - B) < -0.3 の７つの若い星団 (図4) が落ちている ことを指摘しておく。

　(B-V) ギャップを再現する年齢分布は？　

　上の理由のどれが効いているかを特定するため、Battinelli, Capuzzo-Dolcetta 1988 の方法にしたがって、モデルカラー分布を計算した。

g(t) = 年齢分布 (ADF)、(B-V)(t) = モデル星団のカラー進化とする。
星団の (B-V) カラー分布 f(B-V) は、dN = f(B-V) d(B-V) = g(t) dt から、

f(B-V) = g(t)
| d(B-V) / dt |

（B-V)(t)は星団のメタル量に依存するのでは？

ADF g(t) を次のように仮定して f(B-V) を計算した。(B-V)(t) はメタル量 の年齢による変化を入れて、モデルＡ、Ｂで計算した。

a) g(t)=const.

b) g(t)=1/t (つまり dN=dt/t=dlogt なので、log t で平らな分布）

c) 銀河系散開星団の年齢分布(Wielen 1971)

結果を図９に示す。どのケースも双ピークだが、強度比が f(t) によって大きく異なる。


図８.BCDSP 星団、V < 13, の (B-V) 分布。(B-V) < 0 は多数のアソシエーションを含む。 		　モデルカラー分布の検討　

　図９を図８と比較すると、ADF の３つのケース g(t) に対し、

a) ーー＞　赤い(古い？)星団が多過ぎる。

b) ーー＞　LMC の観測分布に適合する。(　CBB88 も同様の結論)

c) ーー＞　青い(若い？)星団が多過ぎる。

図９の結果は、Frenk/Fall82, CBB88の説にも合う。

(B-V) 分布が双耳峰になる原因は、メタル量が次第に上昇する(モデルＡ，Ｂ) 星団 の集合で、UBV 進化の勾配に二つの大きな変化があるからである。その２つは

1) 上部主系列が主に A0 の時代、B-V ＝ 0.3、で起きる。(図１)
　　B-V は ほぼ一定値であったが、その先では log t の１次式で変化する。
　　このため、B-V = 0.5 付近で d(B-V)/dt 最大、f(B-V) 最小となる。

2) 第２の変化は B-V = 0.8 で、そこから進化は青い方へ反転する。これはメタ
　　ルが十分低くて、３節で述べたように２色図上でフック状のカーブを描く
　　場合に起きる。その結果、B-V ＝ 0.6 付近に高メタル中間年齢星団と低メタ
　　ル高齢星団の縮退を招く。

　年齢分布 (ADF) に大幅な変更が必要なわけ　

ただし、細かい点では次のような問題が残る。
a) 青い星団では、モデルでは (B-V) = 0.1 がピークなのに、観測ピークは 0.3。

b) 赤い星団では、モデルピークが 0.8 にピークを持つのに観測は違う。

この差をどう解消できるだろうか？解析の結果は次のような拘束を与える。

a) 青、赤ピークの位置は年齢分布関数 g(t) の勾配に影響されない。

b) モデルカラー進化(B-V)(t) はデータと合う。(図４，５を見よ）

したがって、年齢分布 g(t) の勾配以外に根本的な変更が必要となる。8-4 節で は爆発的な星団形成がより良い一致に導くことを論じる。

　さらに、ストカスティックな効果、赤化、メタル量分散が (B-V) 分布をぼやけた ものにする。しかし、 5-1 節の結果によればこの効果は B-V ≥ 0.4 の星団 に対しては小さく、非常に若い青い星団にのみ効く。いずれにせよ、カラー分散 効果はギャップを埋めるほどではない。


図９. ３つの f(t)とモデルＡ，Ｂの(B-V)(t)に対する 合成 (B-V)分布。
　　(a) f(t) = 一定。(b) f(t) ∝ t-1 (c) 銀河系散開星団とおなじ
　　　年齢分布(Wielen 1971)


　５．４．(U-B) - (B-V) 面上での BCDSP ギャップ

　RGB 出現説は観測と合わない　
　 Bica et al. (1996) データを(U-B) - (B-V) 面上にプロットすると双方で 0.1 mag のギャ ップ、中心は(U-B) ≈ 0.19, (B-V) ≈ 0.47、が現れる。これは 図５で僅か２つの星団, SL 276 と NGC 1861、しか存在しない領域である。

　このギャップは当初 RGB 相転移 ( Renzini, Buzzoni 1986) と解釈された。5-3 節に見たように、この解釈は SSP モデルの結果と合わない。この解釈 (Bica et al 1991) は Buonanno et al 1988 の解析に基づいている。この論文は NGC 1987 の CMD に RGB が存在するとされた。この星団はギャップの赤い側の縁に位置する。 しかし、より最近の論文 Corsi et al 1994 では NGC 1987 の CMD に見られる RGB は周囲のフィールド星によるものとされている。その上、 Corsi et al 1994 に よると、ギャップの赤い側にある二つの星団 NGC 2209, NGC 2108 には拡がった RGB が存在しない。このように、ギャップを赤色巨星の出現で解釈するのは 困難である。

　RGB が見られる最も青い星団は NGC 2190 である。そのカラー B-V = 0.63 は、 モデルで RGB が出現するとされる段階と一致する。



　カラー分散と年齢ーメタル量関係の複合効果　

　ギャップはカラー分散の効果と年齢ーメタル量関係の複合効果である ことを以下に示す。以下の点に注意しよう。

１）図５で A も B もギャップでは、SL276, NGC1861 の点で横切っている。
　　そして、ギャップ部分は下側を回りこんでいる。

２）図７でカラー分散の方向は、ギャップでは進化経路と平行なので、カラー
　　分散が生じない。ギャップより青い側でも赤い側でも分散ベクターの方向
　　は進化経路と交差し、かなりのカラー分散が生じる。
　　その結果、星団の存在しない領域が生じる。これが BCDSP ギャップの上
　　端に対応する。

　こうして、若い星団で赤い側に分散したものがギャップの青い縁を決め、中間、 老齢星団で青い方に分散したものがギャップの赤い縁を決める。ギャップは、 青い星団の赤側への分散の縁と、年齢ーメタル効果で生じたフックに属する 赤い星団の青側へのカラー分散の縁の双方に囲まれた空隙なのである。従って 恒星進化の特別な現象を仮定する必要はない。しかし、図５ではギャップは星団 密度が低い領域である。この点は 8-4 節で論じる。


　６．年齢較正　

６．１．メタルとCMD

星団 CMD の年齢指標　

　文献から年齢を探す代わりに、良いCMDを集めて Bertelli 1994 の等時線から 年齢を再導出する。 よい CMD データの３条件から、表１にある２４星団を選んだ。

　１）CCD 観測

　２）Johnsonの B, V になっている

　３）測光精度

下の３つの等級から年齢を決めた。

　（１）VTAMS = 主系列終端等級

　（２）VRGf = 最も暗いRG星（CHeB段階と考えられる)

　（３）VRGb = 最も明るいRG星（多分AGB)

表１のコメント　

レッドクランプを持つ星団の場合フィールド星の混入が激しいので、（２）の かわりに RC の平均等級を使った。（２）は CHeB というのは 解せない。 References は順にCMD, E(B-V), [Fe/H] の文献番号 。
E(B-V) がない場合 Burstein/Heiles 1984 減光マップ平均 0.07 を適用。
DM = 18.5 (Panagia et al 1991, Bertelli et al 1993) を使う。

メタル量間の不一致が大きい　

E(B-V) は異なる文献同士の一致がよいが、メタル量は方法により大きく異なる値 が出ている。それは、 Elson(1986), Seggewiss/Richtler1989 が集めたWashington, DDO 測光、分光、 CMD データの不一致の大きさから明らかである。

Olszewski et al. 1991 は一様で [Fe/H] が 0.2dex 精度のデータを７０個の赤い星団 から集めた。このサンプルは、若い、および中間年齢星団では Cohen 1982, Cowley/Hartwick 1982 の分光値 [Fe/H] より系統的に大きい。
しかし統一性から、表１はこれを用い、ないものには[Fe/H]=-0.4 (Z=0.008) を 採用する。ただし、二つの星団だけは CMD 文献からメタル量を取った。

　こうして、表の半分（主に赤い星団）だけが個々に決まったメタル量を持つ。 幸い年齢決定に使う指標の内、VTAMS と VRGf はメタル量 影響が小さい。



６．２．等時線による年齢較正


年齢指標となる等級　

Bertelli et al.1994の等時線ライブラリーと MV TAMS　MV CHeB 　MV TAGB から年齢を決める。いくつかコメントする。

　（０）TAMS と CHeB 等級はメタル依存が小さい。 		　（１）TAMS は 6.6 < logt < 10.2 で年齢決定。
　　　　　　log t = 0.33 × MV TAMS + Const.
　　　　　　 MV TAMS の不定性 0.3 等は log t で 0.1 等となる。
　　　　　　メタル量不定性による log t 不定性は 0.1 を越えない。

　（２）CHeB は logt < 8.5 で使用。それより古いと等級が一定になる。
　　　　　　 logt < 8.9 が (1) から確実なら、そこまで使える。
　　　　　　 logt < 6.8 ではマスロスのため (1) しか使えなくなる

　（３）TAGB は　8.0 > logt に使う。メタルに大きく依存。数が少ないので
　　　　本当に AGB 先端かどうか不明な場合がある。

表２には３つの方法で決めた年齢が載っている。「:」が付いているのはメタル量 が不確実で、そのため log t 精度が低いやつ。
でも、使った式が載っていない。いちいち Beretelli et al 1994 の等時線 と付き合わせているらしい。 MV TAMS の具体的決め方が不明。これも実例で 確かめろ、か？

表２． 表１に載った星団の年齢。３通りのそれぞれで決めた値＋平均値


表１．ＣＭＤが公刊されているテンプレート星団とそのメタル量。

　６．３．個々星団へのコメント　


NGC 1711 ( Sagar et al 1991a)　

　赤色超巨星の塊り V = 15.0 付近にあり、 V = 14 の主系列終端より明瞭。しかし 多くの青い星が V < 15.7 に存在する。これを主系列終端とする。


　NGC 1711

NGC 2004 ( Sagar et al 1991a )　

　はっきりした赤色超巨星の塊りが 13.0 < 13.5 にあり、青い星の系列は 13.5 で突然終わっている。 MV TAMS = 13.5 に取ると、赤色 超巨星と主系列終端とからの年齢に大きな差、Δlog t = 0.6、が生じる。 V = 14.3 にある二つの星を主系列終端とすればこの矛盾は解消する。しかし、 その場合、最も明るい青い星をセファイドループと解釈するのは難しい。それら が赤色超巨星より暗いからである。


　NGC 2004

NGC 2100　( Sagar et al 1991a )

　NGC 2004 と似て、赤色超巨星の塊りがあり、主系列終端は V = 13.5 - 15.0 のどこかはっきりしない。 MV TAMS = 14.3 と一応したが不確定で ある。それとは独立な問題として、 V = 12 まで達する青色超巨星の数が多すぎ る。 V = 14 より暗い赤色超巨星が二つあるが、赤色超巨星の大部分は V = 13.4 と V = 14.0 の間に分布する。青い星と赤い星とで決めた年齢に大きな差が生じる、 という NGC 2004 と同じ問題が存在する。


　NGC 2100

NGC 2164　( Sagar et al 1991a )

　赤色超巨星の塊りと主系列終端の双方がしっかり認められる。
主系列終端は V 何等か？MS から RSG への弧は何？


　NGC 2164

NGC 2214　( Sagar et al 1991a )

　二重星団であり、二本の赤色超巨星系列を持つ。これは年齢の異なる星団が 融合したためと考えられている。若い星団は５つの赤色超巨星、V ≈ 15.5, B-V ≈ 1.3 の固まりではっきり定義されている。 V = 13.3 に明るい 赤色超巨星が一つあるが、明るい赤色星は V = 14.4 までの所に集中している。 主系列末端もはっきりしている。


　NGC 2214

NGC 1858 (Vallenari et al 1994b)　

　進化した赤い星を含まない。主系列端末のみが年齢決定に使える。


　NGC 1858

NGC 1850 (Vallenari et al 1994b)　

　二つの集団：非常に若く重い星からなるグループ(NGC1850A。図では領域B)は V ≈ 16.5 で主系列から離れ、 V ≈ 13.0 まで伸びる。より高齢の 第２グループ(図の領域Ａ)は主系列端末と赤色超巨星の集まりが明瞭に認められる。
全然そんな風にみえないけど。


　NGC 1850

NGC 1866 (Chiosi et al 1989), NGC 2010 (Mateo 1988a)　 NGC 2134 (Vallenari et al 1994a)

　これらの星団では主系列終端、赤い巨星の最大光度、最低光度は容易に決定 できる。それはフィールド星の混入が適切に処理されているからである。しかし、 VRGf からと VTAMS からの年齢の間には系統的にずれ が見られる。t(VRGf) は t(VTAMS) より Δlog t = 0.3 大きい。この差をなくすには、赤色巨星と主系列終端の間の等級差を 1 等 小さくする必要がある。測光エラーはそんなに大きくない。

　NGC 1866




　NGC 2010





　NGC 2134


他の星団　

　他の星団はCorsi et al 1994 から採ったのでデータは一様である。 CHeB 期の星は RC に集中しており、その平均等級は容易に得られる。NGC 1868 より若い星団では CVHeB 等級はメタル量依存が少し見られる。t(CHeB) と t(TAMS) の一致は良い。








　NGC 1711











　NGC 2004











　NGC 2100







　NGC 2164










　NGC 2214






　NGC 1858










　NGC 1850











　NGC 1866





　NGC 2134



　NGC 2190 より古い星団では年齢は TAMS のみで決められた。この場合、 測光エラーと周囲の星の混入により年齢決定の不定性は少し大きくなる。 　




　６．４．年齢決定へのコメント　


TAMS と CHeB 年齢の差　

　表２を見ると、暗い赤色巨星から決めた年齢は一般に、主系列端末から の年齢とよく合うことが分かる。しかし、古くなると、赤色巨星から決める 年齢は主系列より系統的に log t で　0.1 から 0.6 大きくなる。これは モデル等時線で主系列末端と CHeB 期との等級差を大きく見積もりすぎて いるか、またはこの差を観測が小さく測っているかである。それらが起きる 原因としていくつか考えられる。

（１）連星のため、主系列末端を 0.6 等くらい上げてしまう。

（２）モデル Mbol から Mv への変換は温度に関係したエラーが出る。

AGB 上端 年齢の抱える問題　

　AGB 上端から決める年齢は前二者に対して緩い相関を持つ。この年齢が大きな メタル量依存性を抱えていることを考えると、前二者との差の多くはメタル量 の不定性に帰せられる。その上、観測された最も明るい星が本当に AGB 上端 に対応するかどうかは不明である。

　その理由は、

（１）上端付近の星の数が少ない。

（２）ＣＭＤで近くに RGB 星がいる。

（３）星団年齢　

球状星団年齢　

AGB 上端年齢の誤差が大きいので、表２では前二者の単純平均を載せた。年齢は log t = 9.2 までに及んでいる。前に述べた如く、 3 Gyr から 10 Gyr までの 間には星団が見つかっていない。

　この年齢サンプルに LMC に属する古典的球状星団 NGC 1466, NGC 1786, NGC 1841, NGC 2210, NGC 2257, H11 を加えると完全に前年齢範囲が覆われる。
　これらの星団の年齢はそれ自体が複雑な問題なので、あえて年齢を付加せず、 必要な場合には 15 Gyr とした。


　７．積分カラーからの年齢　


　７．１．Elson,Fall 1985 法の改良


EF85 法の不定性　

　有名な Elson,Fall 1985a で、彼らは積分 UBV カラーから年齢を求める 方法を与えた。ここに示したように実際の星団はそのカラーを分散させる 多くの影響を受ける。したがって、年齢だけでカラーが決まるわけではなく、 EF85 法には多くの不定性が含まれる。ここではそれを改良する２つの方法を 提案する。

Ｓの意味　

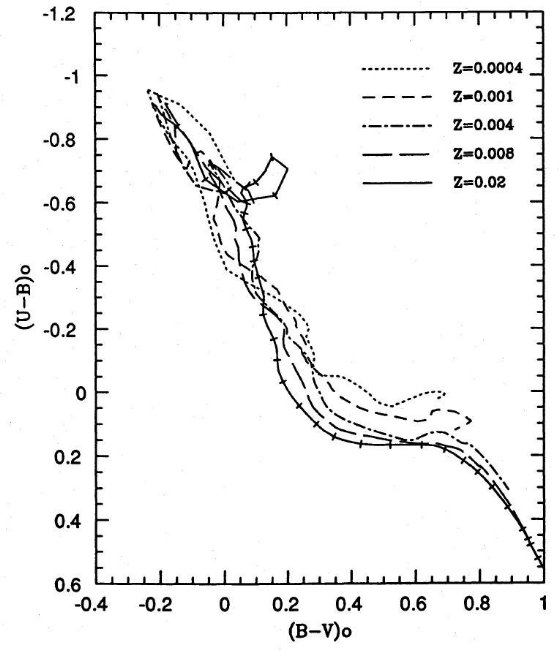
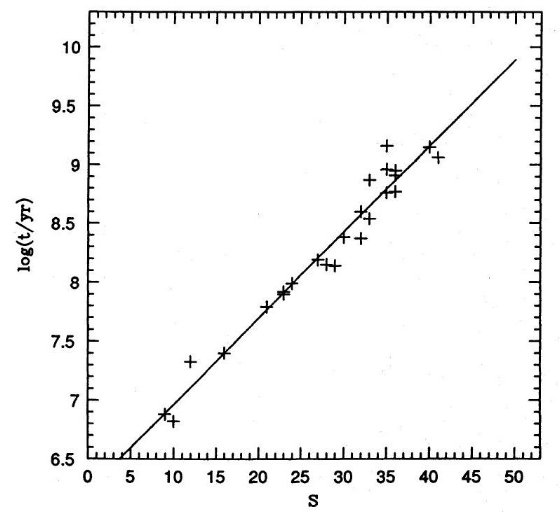
　既に 2.1.節に述べたが、(U-B, B-V) 面上での SSP のカラー進化は log t で測って一定のスピードで変化する。これは太陽メタル量付近では特に そうであり、例外は 107 年付近での赤色超巨星出現のあたりのみ である。したがって、EF85 の経験的な方式が成功したのは当然であった。 もし我々が (U-B, B-V) 図を等しい大きさの区間(パラメターＳ)で区切れば 単純な線形関係が S と log t との間に成立するであろう。

Ｓは古い星団に弱い　

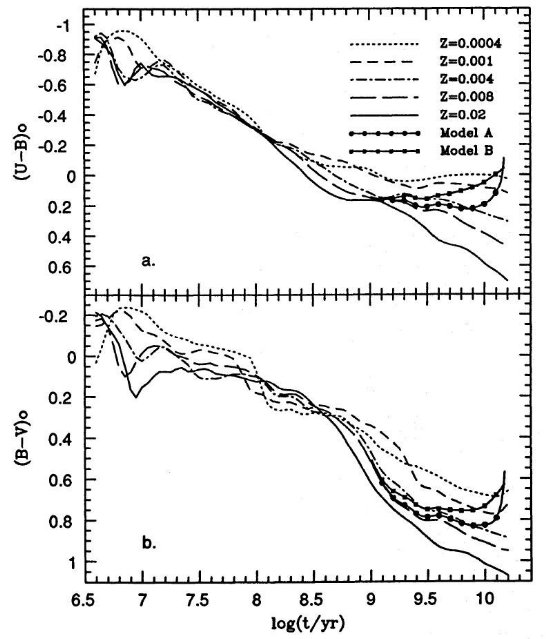
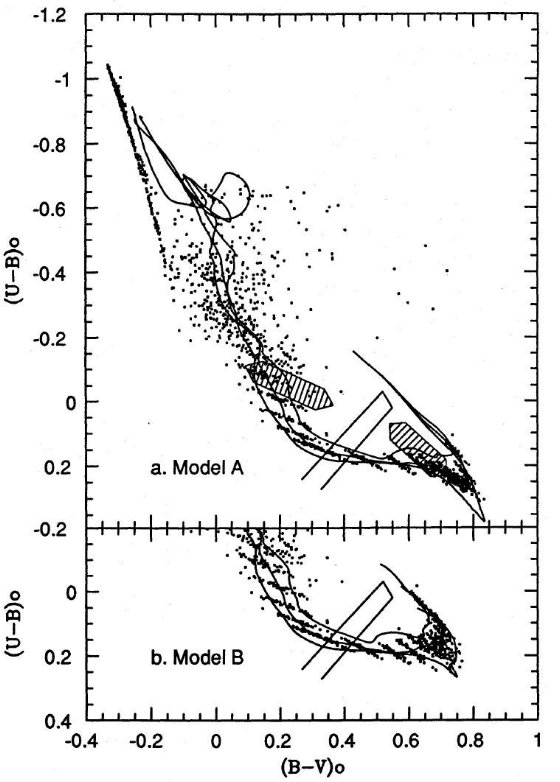
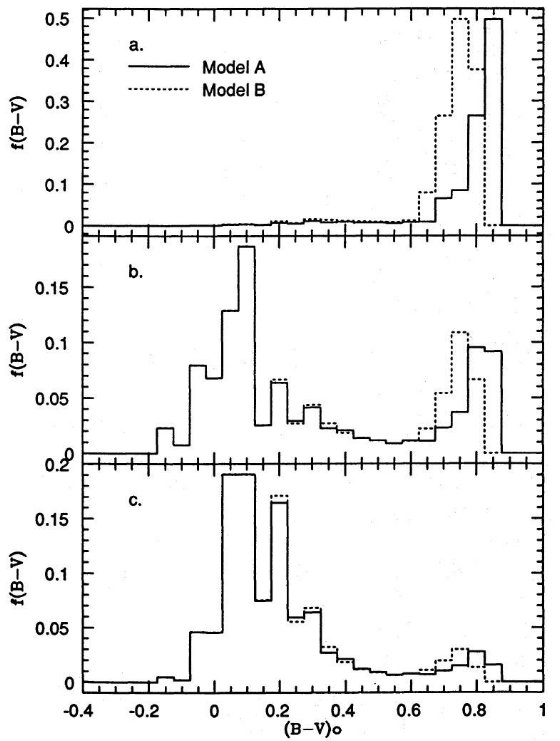
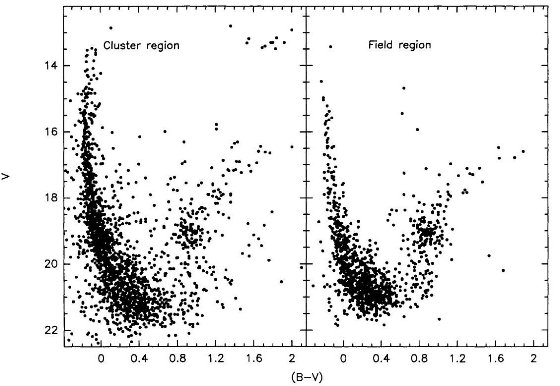
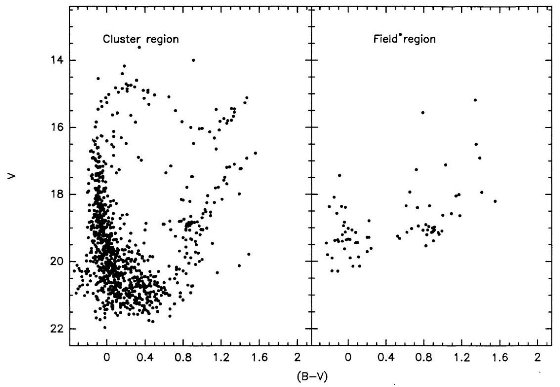
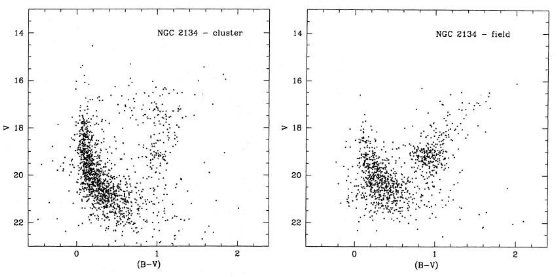
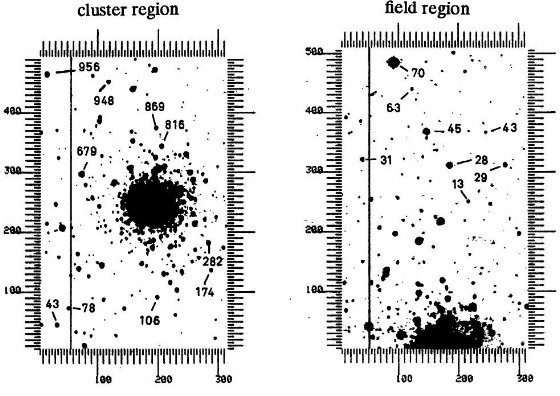
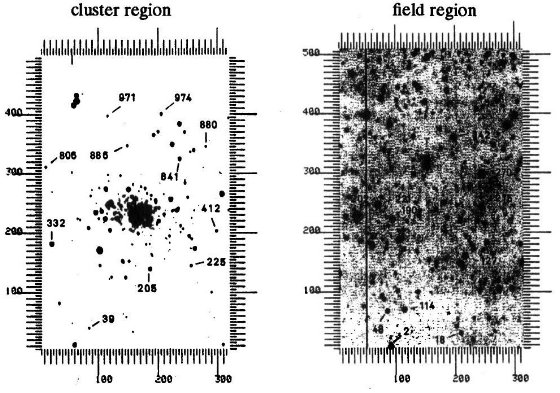
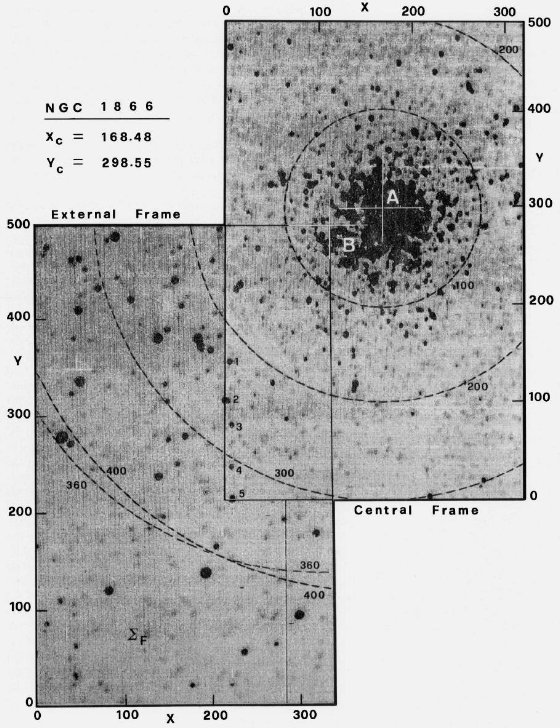
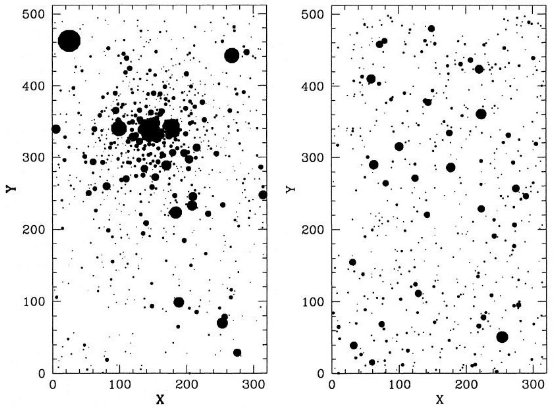
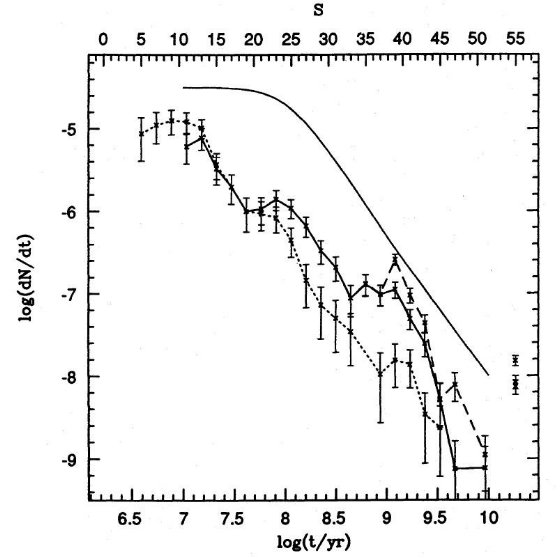
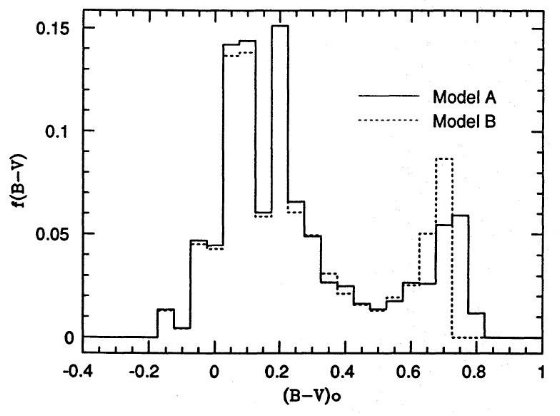
　しかし、 EF85 には、星団の年齢が変わるとメタル量が変わることを考慮 すると、大きな欠点がある。古い星団では S と log t の間の線形関係は 成立しなくなる。これは図１、図３のモデルＡとＢを見ると分かる。古い 星団は小さな log t の間にカラーの大きな変化を示している。実際、カラー の内在的分散を入れると、この系列の星団は全て同年齢と言ってよい。 このように古い星団のＳパラメターを並べることは、同一年齢でメタル量の 増加して行く順を示すもので、同一メタル量で年齢の増加していく系列と 考えるべきでない。この年齢領域の星団には S 法は信頼できる年齢を与えない。

Ｓがギャップを表わさない理由　

　EF85 で導入された S は 3 Gyr - 12 Gyr のギャップを表わしていない。これは Ｓが大きな星団をつなぐラインに沿って決められたからである。５−２節で 述べたように、年齢ギャップは (U-B, B-V) 面上では見えない。これが EF85 が van den Bergh 1981 サンプルでは、ギャップも星団の爆発的形成もないと述べた 原因である。

　７．２．Ｓパラメターの定義　


　新しいＳ系列　

　先の議論から我々はＳ系列を定義し直すことにした。EF85 と異なり、E-SWB VII の古い星団はこのＳパラメター法の適用から外す。それらは CMD から全て古典的な球状星団 (van den Bergh 1991) とされている。それらに対しては一律に log t = 10.2 (15Gyr) とする。 　Ｓパラメターを導くやり方は次の通りである。

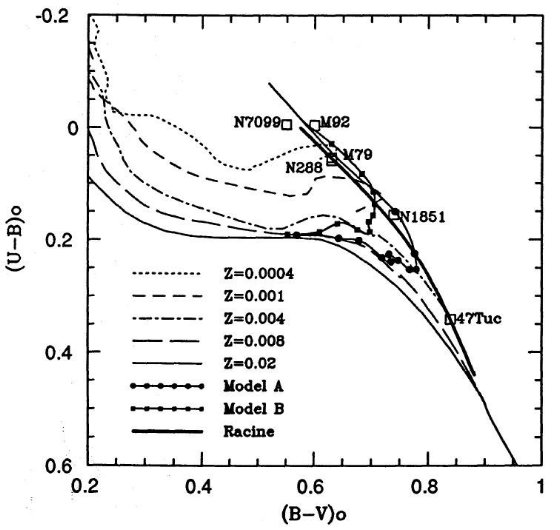
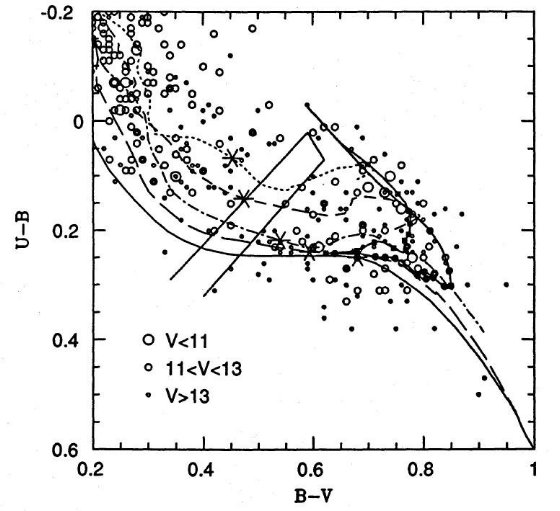
（１）EF85 図１０のＳカーブを Z = 0.008 の SSP 経路(図４）と比較する。
　　　B-V < 0.5 では ２本のカーブが一致していることが分かる。
　　　B-V > 0.5 では ２本のカーブは大きく離れる。

（２）EF85 のＳカーブは E-SWB V 型星団、NGC 2190, NGC 2162, NGC
　　　1806、の下側をなぞっている。それに対し、SSP Z = 0.008 カーブは、
　　　E-SWB V 型星団の平均値を貫いている。そこには他の星団 NGC 1783,
　　　NGC 1644, NGC 2154 がそんざいする。

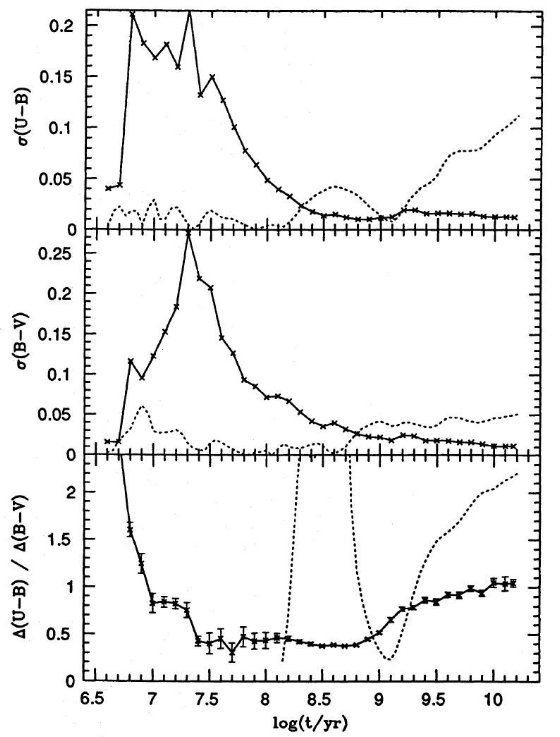
（３）5-4節で議論したように、V, VI 型の分散方向は Δ(U-B)/Δ(B-V) ∼ 1
　　　したがって、我々は E-SWB V, VI 星団の分布を Z = 0.008 系列からの
　　　分散として解釈したい。これを B-V = 0.8 まで妥当と考える。 		（４）この先 Z = 0.008 系列は U-B が増加し続ける。しかし、S カーブの細
　　　かい形は重要でない。その辺には星団がほとんど無いからである。

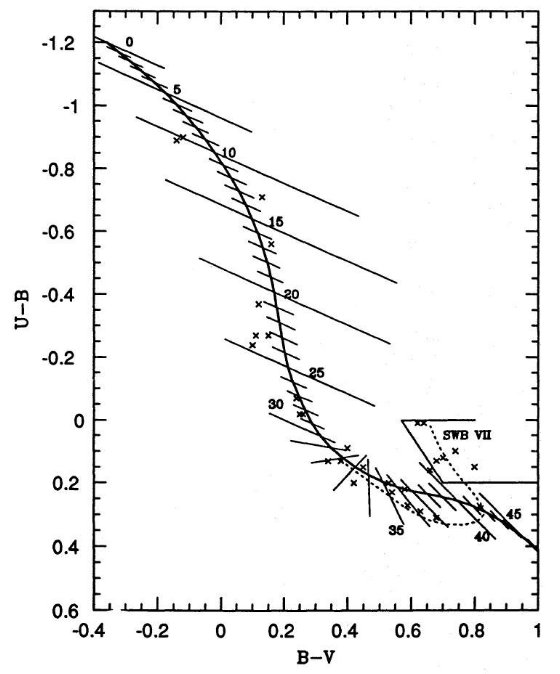
（５）最終的に採用する S カーブは B-V < 0.5 では EF85 カーブ、その先
　　　0.8 までは SSP Z = 0.008 を使う。合成ラインを図１０に示した。

星団にＳ値を付ける　

　Ｓカーブ上にない星団からは分散の方向に線を延ばして、カーブとの交点をその 星団の S とする。分散方向の傾きは、青い星団で Δ(U-B)/Δ(B-V) ∼ 0.45
青い星団では 1 である。S = 30 - 36 では分散の方向が S カーブと平行なので 特別の注意が必要である。そこでは星団に S 値を付けることが難しい。

　同様の困難は非常に若い ( ∼ 107 yr ) 星団でも起きる。そこ ではストカスティックな過程で大きな分散が起きる。

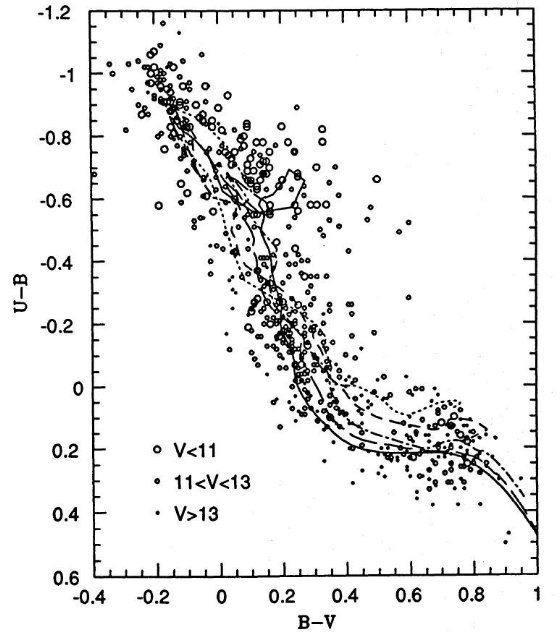
　カラー分散の方向が S カーブに直交していないという効果を無視すると、 赤い方に分散した星団の年齢を過大に評価し、青い方に分散した星団の年齢を 過小に評価するだろう。van den Bergh 1981 データにこの方法を適用すると、 古い方法の時と同じような年齢を与えるだろう。それはこのサンプルはカラー分散 がほとんど無いからである。対称的に BCDSP データにはかなりの違いをもたらす。

　図１０　採用したＳパラメター。クロスは年齢較正に用いた星団。
　　　　　SWB VII と名付けた領域には非常に古い星団が存在する。


　７．３．年齢 - Ｓ 較正　


CMD から年齢が得られた星団の S 値　

　CMD から年齢を決めた星団の S パラメターを評価した。表３がそれである。 EF85 で決めた S 値も載せた。

　図１１に園 S 値を log t に対してプロットした。直線フィットすると、

　　　　　log t = (6.227±0.096) + (0.0733±0.0032)S

log t での rms 分散は 0.137 である。この関係式の勾配は CBB88 と EF85 の 中間である。


　図１１　CMD から年齢が得られた星団の S - log t 関係。実線は最小二乗
　　　　　フィット

表３　CMD から年齢が得られた星団の S 値。 EF85 の S も載せた。


　７．４．年齢分布　


ギャップとピーク　

　上の関係式を BCDSP 星団に適用して年齢を決定した結果が図１２である。 E-SWB VII型星団は　log t = 10.2 を仮定して図の中に足した。

　図１２を見ると 44 < S < 54 にギャップが存在することが分かる。 これは 9.4 < log t < 10.1 に相当する。また、二つのピークが S ≈ 23 と S ≈ 39 に見えるが、これらは 108, 109年に相当する。

107年のピーク　

　これらのピークは星団形成が活発であった時期を表わしている。S = 10 数 107年付近にも別のピークがあるが、これを同様に解釈して よいかは疑問である。と言うのはこのくらい若いと、サンプル中に星団以外 の天体も多数紛れ込んでいるからである。

　この年齢分布は van den Bergh 1991 の年齢分布と極めてよく似ている。 彼の図は Sagar, Pandey 1989 の集めた年齢データに基づいている。

図１２　下軸：BCDSP 星団の S 値分布。 上軸：log t 。
　　　　実線は全星団。点線は V < 13.0

　８．改訂された年齢分布関数　


　８．１．光度低下線　


　図１２に示された星団年齢の分布は星団の形成と破壊の歴史全体だけでなく、 恒星進化に伴う星団光度の低下を反映している。この効果を抽出するため、 同じ光度で出発する星団の集合の年齢分布をシミュレートする必要がある。

　図１３は BCDSP 星団の年齢と等級の分布図である。それに重ねて Z = 0.008 SSP 光度低下線を引いた。IMF の傾きは x = 1.35 と x = 2.5 の２種を取った。 x = 2.5 では、全期間を通して V < 13.0 を保つ星団グループを得ることが 可能である。一方、 x = 1.35 の場合 log t > 8.5 でサンプルは不完全となる。 そのような場合、 V > 13.0 星団のサンプル不完全度の評価も必要となる。




図１３ ＢＣＤＳＰ星団の年齢と等級の分布。
　　　　Z = 0.008 Mtot = 103, 104, 105 Mo の SSP 光度低下曲線を重ねた。
　　　　実線 : x(IMF) = 1.35, 点線：x(IMF) = 2.5

　８．２．不完全度の補正　


　図１４は異なる S 値 (年齢) 毎の光度関数を示す。明らかにＬＦは年齢 区間同士で異なっている。特に古い星団では指数関数則によく乗っていること が分かる。LF が V = 13 の先で落ちているのはサンプル不完全度が影響して いることを示唆する。

　x = 1.35 IMF の場合、34 < S < 50 で既に不完全度の補正が必要となる。 そのため、まず 11.0 < V < 13.25 で IMF を log n(V) = -5.2 + 0.48 V で フィットする。これは、n(L) ∝ L-α で α = 2.2 に 相当する。Elson, Fall 1985 は α = 1.5 を得ていた。

　この式が 34 < S < 50 で V = 14.0 まで適用可能と考え、不完全度を 期待値と観測星団数との比で定義する。すると、V = 13.5 で 1.1, V = 13.75 で 2.8, V = 14.0 で 8.3 であった。

　古い星団 (E-SWB VII) の不完全度の評価は問題である。先ほどの式をそのまま 使うためには適用範囲を V = 14.0 まで拡大する必要がある。これは危険である。

図１４ 異なる S 値 (年齢) 毎の光度関数。
　　　　34 < S < 50 では log n(V) = -5.2 + 0.48 V (11<V<13.25 でのフィット)
　　　　を重ねた。

　８．３．　改訂した年齢分布関数　


　年齢分布関数 ( ADF ) の決定　

　ΔS = 2 のビン内で質量で制限した星団カウントを行い、不完全度を 補正して星団の年齢分布関数 ( ADF ) を決めた。図１５はその結果である。 ADF の二つのコブが目立つ。一つは log t ≈ 8.0, もう一つは 9.1 に ある。これは図１２に見たコブと似ている。さらに、 9.6 < log t < 10.1 に年齢ギャップが存在する。log t ≈ 7.0 のコブには多数のアソシエー ションが含まれ、これらの詳しい検討はこの論文では行わない。最後に古い 星団の ADF は実際の ADF への下限を与える。なぜなら、おそらくこの論文で 使った補正用の不完全度は大幅に過小評価されているだろうからである。

コブとギャップの意味　

　図１５に示した ADF は LMC における星団の形成と破壊の歴史を物語っている。 サンプルに一定の割合で働く破壊過程だけでは滑らかな ADF を産み出すだろう。 その良い例は Wielen 1971 が求めた太陽近傍の散開星団の ADF である。星団 の力学的な溶解分裂過程 (Wielen 1991 ) は銀河系でも LMC でも同じであろう から、LMC 星団 ADF に見られるコブとギャップは、星団形成率が実際に増大、 減少したことを意味する。

現在の LMC 星団形成率　

　図１５の ADF には任意シフトは含まれていない。108年以下の若い 星団はまだ力学的な溶解分裂過程を受けておらず dNc/dt の値は現在の LMC 星団 形成率の下限を与える。108年において、 dNc/dt ≈ 10-6星団/年 である。もし、 V < 13 の全クラスターを対象に して適切な年齢星団を考えれば少なくともこの４倍は行くだろう。この値は したがって、Hodge 1988 が得た 2.7 × 10-6星団/年 と 合致する。

星団形成率変化の平均勾配　

　ADF の平均勾配に関し、この値が銀河系より低いことが潮汐力が LMC では 弱いため破壊率が低いのであるという解釈が行われた。しかし、

（１）ADF 勾配は IMF 勾配の影響を強く受ける。実際、x ≥ 2.5 では銀河系 より急な ADF が得られる。IMF 勾配には不定性がある上、星団毎に変わるという 指摘 (Mateo 1990) さえある。

（２）LMC 星団形成史にある不連続性を考えると平均変化率を考えることに意味 があるか疑問である。

星団形成率の増大期　

　ADF のコブの時期は他の研究で見出された星団・恒星形成率の増大期とよく 一致している。例えば、Mateo 1988b は LMC 周辺部の 31 星団 CMD を調べ



図１５　x = 1.35 (実線), 2.5 (点線) を仮定した年齢分布関数 (ADF) 。
　　　　x = 1.35 に対しては不完全度を補正した ADF (太い破線)も示す。
　　　　エラーバーはサンプル数の統計的不定性。
　　　　細い実線は Wielen 1971 による太陽近傍 ADF 		て、 2 - 4 Gyr 昔に星団形成が盛んであったと結論した。Frogel et al 1990 は　 LMC 星団内 M 型星のカラー分布に二つのピークがあり、それらは ≈ 100 Myr と ≥ 1 Gyr とに対応するとした。この二つのピークは LMC バーの M 型星にも見られる。Frogel, Blanco 1983. Wood et al. はフィールド LPV とセファイドの周期分布と光度分布に同様の星形成増大期の証拠を見出した。 Bertelli et al 1992 は選択領域の CMD を解析して、大規模な星形成が ∼ 4 Gyr 昔から開始されたとした。

以前の研究との差　

　EF85, Elson,Fall 1988, CBB88 は星団形成率の増大期や極小期は見出さな かった点で我々の結論と異なる。 この差の原因の一部は BCDSP データにより 統計的に van den Bergh 1981 よりよいデータが提供されたこと、一部は パラメターＳを得る際に分散ベクトルの方向を考慮したことにある。しかし、 主要な理由は赤い星団の年齢を決める際に彼らと別の方法を採用した点にある。

　８．４．カラーギャップへの年齢分布関数の影響　


ギャップでの観測とモデルの差　

　5.3 節, 5.4 節では、(B-V) カラー分布、(U-B, B-V) 面上双方でのギャップ は、LMC 内のメタル増加を入れた星団の連続的な年齢系列で自然に説明される と結論した。しかし、モデルと観測の微妙な差は我々が完全に正しい ADF を 得ていないことを示唆する。

ADF と カラー分布のピークの一致　

　B-V の双耳峰分布に関して、ADF の二つのピーク, 107年と 108年 は (B-V)o = 0.2 と 0.7 に対応することを注意する。 これらは、(B-V) 分布のピーク位置と一致する。ADF の形が (B-V) 分布の 双耳峰性を強調しているのだろうか？この点をテストするため、解析的に 表わした ADF f(t) ∝ t-1 にピークやギャップを加えて (B-V) 分布のシミュレーションを行った。

ADF(t) にピークを入れたら　

　図１６には実験の結果が示されている。図9b の f(t) ∝ t-1 と較べると以下の違いが明らかとなった。

（１）9.3 < log t < 10.1 にギャップを加えると赤いピーク、(B-V)o ≈ 0.8 は下がる。

（２）8.0 < log t < 8.5 と 9.0 < log t < 9.3 にコブ を加えると、(B-V)o = 0.2 と 0.7 のピークを高める。

　シミュレーションに現れた (B-V)o = 0.1 の大きなピークは log t = 7.1 で　d(B-V)/dt がゼロに非常に近くなる結果生じたものである。しかし、そこ ではストカスティック効果が大きくカラーの分散によりピークは消えはしなくとも 大きく下がるのである。

ADF(t) にギャップを入れたら　

　(U-B, B-V) 面上でのギャップに関しては、これが S ≈ 34 で生じて いることに注意しよう。年齢では 500 Myr に相当する。ギャップ領域 で、進化経路に沿って星団数が少ないのは 100 Myr と 1 - 2 Gyr との二つの 星団形成増大期に挟まれた減少期に相当する。これは、図５の BCDSP ギャップ のボックス下側の縁に対応する。ボックス上側縁は 5.4 節で述べたカラーの 分散の結果である。この様な BCDSP ギャップの理論的な説明は、観測と同じ 数の星団を使い、適切な AMR, カラー分散、年齢分布 f(t) を取り入れた


図１６　年齢分布 f(t) を仮定した B - V 分布のシミュレーション結果。
　　　　 f(t) にはピーク、ギャップが繰りこまれている。

　９．結論　


　主な結論はアブストラクトに述べてあるので、最後の考察を行う。

(U-B, B-V) 面を滑らかに動いて行く SSP の進化モデルから、LMC 星団の 観測カラー分布を導くことが出来た。その時の条件は
（１）適切な AMR
（２）自然な原因によるカラーの分散
（３）カラー分布の詳細まで合わせるための ADF のピークとギャップ

SSP 自体に急激なカラー変化を引き起こさせるような仮説は必要ない。

　８．