|
背景 銀河系の化学、運動学的性質を探るには数万の星、将来は数百万、の分光 サーベイが必要となる。それには自動解析が必須である。いくつかの現在 進行中の分光サーベイは Ca II 三重線 ∼ 8500 A を含む波長帯を 選択している。本論文はそのようなスペクトルの自動解析を目指す。 目標 スペクトルから、Teff, log g, [M/H] を得る方法を開発する。パラメタ―空間 での縮退を研究し、得られたパラメタ―に誤差を評価する。 方法 二つのアルゴリズムを研究する。両方とも、観測スペクトルを人工スペクトル のグリッドと比較するのだが、数学的手法が違う。 (1)第1の方法は MATTISSE と呼ばれ、スペクトルの局所的なフィットから パラメタ―を導く。波長空間の各ピクセルは独立に扱われ、与えられたスペクトル の値に対する各波長でのフラックスの敏感度を人工スペクトルから決定する。 この敏感度ベクトルを使って、観測スペクトルを投影して星のパラメタ―を得る。 |
第2の方法 DEGAS はパターン認識法を採用し、当然ながらパラメタ―空間全体
を見渡す。観測と人口スペクトルを比較して行き、波長帯全ピクセルで総計し、
追加の補正を加えて、決定ツリーを辿る。
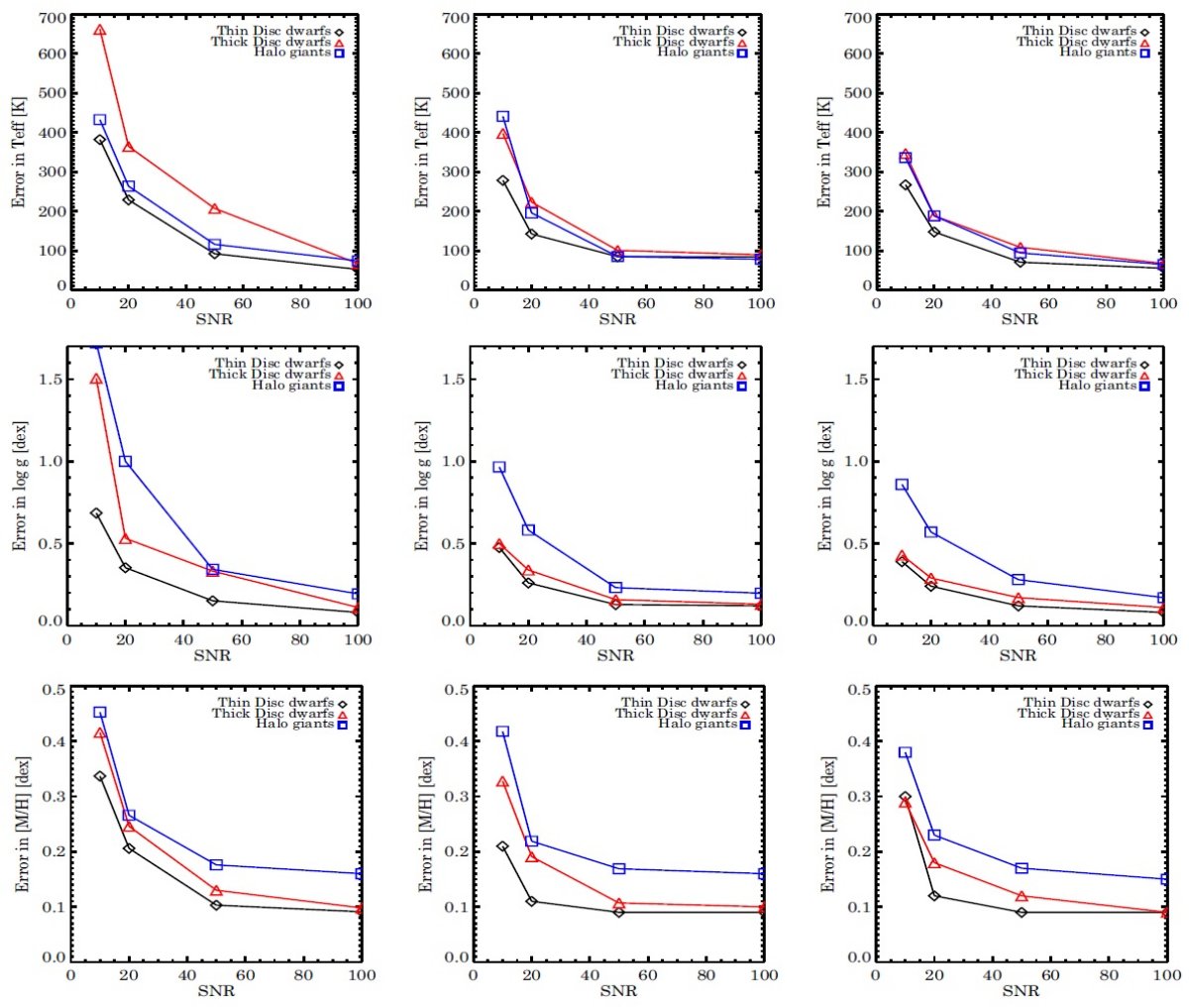
結果 HR 図上の様々な個所で、パラメタ―の縮退が見つかった. 高温の矮星と巨星 は同じスペクトルの特徴を持つ。低温矮星では log g を決めることが難しい。 実験から、局所法は S/N 比が高い場合有効と分かった。決定ツリー法は S/N 比が低くなると有利になる。そこで、二つを組み合わせ、薄い、厚い円盤星なら S/N = 20 まで、ハロー星なら S/N = 50 なら銀河系考古学に十分な精度の結果が得られることを示した。 結論 パラメタ―縮退は距離や空間速度のような量に系統的な誤差を生む原因となる。 |
|
Ca II 三重線領域のライン そこには Ca II 以外に Ca II, Si I, Mg I の α 元素ラインがあり、 低分散でも検出可能である。これ等のラインと Fe との強度比は元素進化の 研究に使え、また Ca II 三重線は [M/H] の評価に役立つ。その上、パッシェン ラインは G3 より早期の星で見える。 Mg I 8807 A は log g の決定に有用である。 低温度星では CN, TiO が見える。 大量分光データ RAVE は 8410 - 8795 A, R = 7500, I ≤ 13 の UK シュミット 6dF 多体分光器 を使い、 40 万体以上のスペクトルを集めた。 DART は FLAMES/VLT で Ca II 三重線領域スペクトルで銀河系考古学を研究した。 GAIA はその Radial Velocity Spectrometer (RVS) R = 11500 で 数千万のスペクトル を集めるだろう。 |
パラメタ―の縮退 この領域では、 Teff と log g の強い縮退が起きる。そのため、巨星と矮星の取り違い がしばしば生じる。この縮退をほぐす方策が必要である。 自動解析プログラム Bijaoui et al 2010 にあるように、いくつかの自動解析プログラムが存在する。 (1)最小距離法: Nelder-Mead アルゴリズム、ガウスーニュートンアルゴリズム (2)与えられたベクトルへの投影を最適化。主成分解析。MATISSE アルゴリズム (3)人工神経ネットワーク、決定ツリー。 |
|
MATrix Inversion for Spectral SynthEsis = MATISSE 詳しくは Recio-Blanco et al 2006, Bijaoui et al 2010 を見よ。 θi(star) = Teff, log g, [M/H] の評価値とする。それは 観測スペクトル O(λ) を特別なベクトル Bθ(λ) に 投影して得られる。 θi(star) = Σλ Bθi(λ)O(λ) (1) このベクトル Bθ(λ) は人工スペクトルライブラリー を用いた訓練フェイズの間に計算される。人工スペクトルは観測と同じ波長域 と分解能のものを使用する。 Bθ(λ) が直交していれば 大気パラメタ―は正確に決められる。そうでないと縮退が生じる。 Bθ(λ) Bθi(λ) が以下のように表されると仮定する。 Bθi(λ) = Σjα ijSj(λ) (2) ここに、Sj(λ) = j-種人工スペクトル。αij = ウェイト。(1)に(2)を代入すると、 θi = Σλ Σjαij Sj(λ)O(λ) = Σj[αijΣλ O(λ)Sj(λ)] = ΣjCijaj (3) ここに Cij と aj は Si と Sj の 相関行列とウエイトのベクトルである。 ( 「ウエイトのベクトル」の意味不明。) |
Thevenin, Bijaoui, Katz 2003 による解説(分かり易い) Thevenin, Bijaoui, Katz 2003 "Chemical Abundances from GAIA Spectra" in "GAIA Spectroscopy, Science and Technology" ASP vol 298 によると、 特性ベクトル(スペクトル)B(k) は参照スペクトルの一次結合で与えられる。 B(k) = Σi=1,IαiSi(k) ここに、k = 1, K は波長番号、i = 1, I は参照スペクトルの番号である。 重み αiの決定が問題である。 j-番星の物理パラメターΘj は、B(k) に Sj(k) を投影して得られると仮定する。 Θj = Σk=1,K B(k)Sj(k) (波長積分に相当) = Σk=1,KΣi=1,Iαi Si(k)Sj(k) = Σi=1,I[Σk=1,KSi(k)Sj(k)] αi = Σi=1,ICjiαi Cji = Σk=1,KSi(k)Sj(k) は、参照スペクトル同士の相関行列である。したがって、その逆行列 Rij を参照スペクトルのパラメタ―に掛ければ、重み αi が得られるであろう。 αi = Σj=1,IRij Θj |
|
規格化スペクトル MATTISE 法は規格化スペクトルを扱い、したがって大気パラメタ―の情報は 吸収線強度に全て収められている。ノイズや、モデルスペクトルと実際の スペクトルとのズレなどを考えると、有効温度、重力、メタル量などのパラメタ― に関係するライン強度を考慮し、その他のラインへの重みを減らすのが賢明であろう。 何次までの近似を行うか? その最適化は、B(λ) を計算するときに、具体的には相関行列 Cij を逆変換する際に行われる。直接の変換は、パラメタ―に起因 する全ての n-次の変化を考慮する。 ( スペクトルとパラメタ―の非線形関係?) しかし、スペクトルの1次の変化だけでよいなら、 C 行列の逆変換の近似解を求めるべきである。 近似の次数は、例えば Landweber 1951 のような逐次アルゴリズムを用いれば制御可能である。 逐次回数 実際には相関行列は不良条件になることが多い。その時には固有値の多数がゼロとなる。 Landweber アルゴリズムでは、行列条件に応じた変換を適用する。その意味は、第一固有ベクトル は第1逐次近似の際に逆変換され、最小固有ベクトルを得るにはより多数回の逐次近似を 必要とするということである。 |
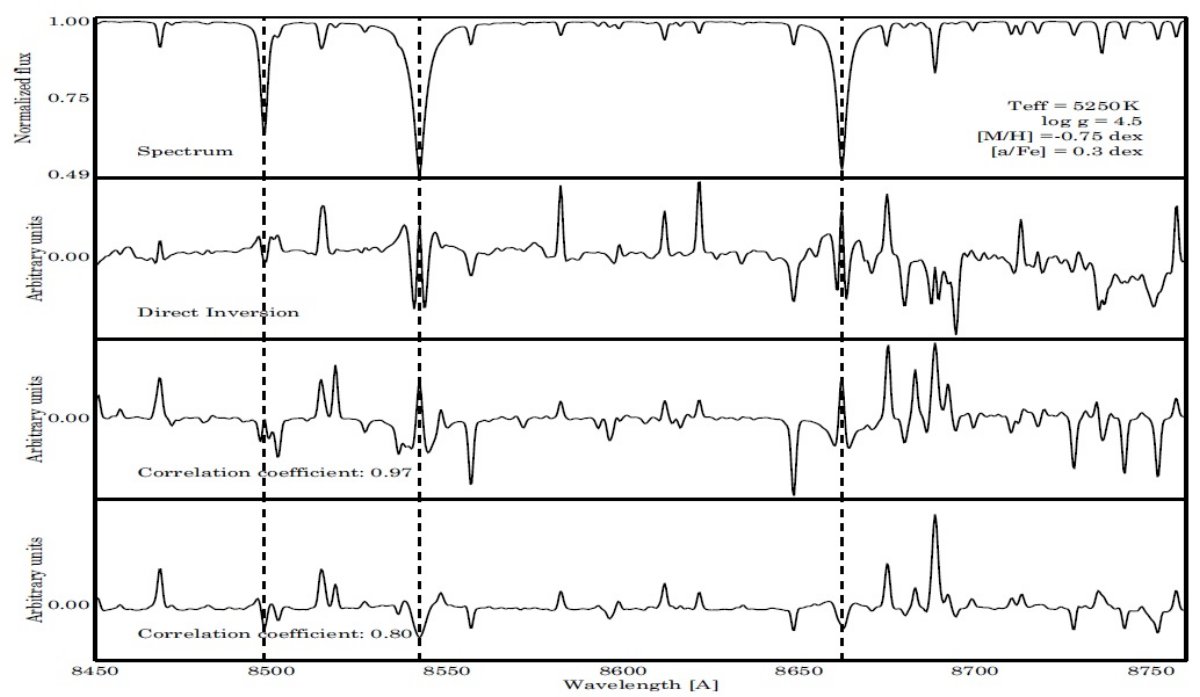
相関値に応じた特性ベクトル 3.1.節で述べた人工スペクトルのグリッドをとり、異なる相関値 0.75, 0.80, 0.90, 0.95, 0.98 に対して、逐次近似を止めた。 ( 全然分からない。) そして、対応する C-1 から特性ベクトル Bθ(λ) を計算した。図1に異なる相関値に対応した Bθ(λ) を示す。 図を見ると分かるが、相関値 0.80 の場合(図1下)、スペクトルの弱い吸収線は全て 非常に弱い重みしか与えられない。このような近似的 Bθ(λ) はスペクトルの精度が低く、弱いラインがノイズに埋もれるような場合には最適で ある。 最適な結合 様々な近似度の Bθ(λ) をノイズの高いスペクトルに適用 することで、最適な結合を得ることができる。 ( これも意味不明。) |

|
原理 人工スペクトルのグリッドをパターンの集合と考え、その中に観測スペクトル と同じものを探す方法である。人工スペクトルを使って、教育期に認識規則が 確立される。 決定ツリー 決定ツリーはデータマイニングの世界では普通に使用される手法である。ツリーの 分岐点毎にデータセットはさらに数個のサブセットに分割される。葉っぱレベルまで 来る=同定である。k - 次 ツリーは k - 次元(ここでは k = 3, Teff, log g, [M/H]) 空間ないでの基礎的な分割構造である。決定は分岐ベクトルへの観測の投影から 得られる。古典的、つまり軸平行型、の決定ツリーは各分岐点で一つの変数しか扱わない。 特別な場合、オブリーク決定ツリーの場合、分岐ベクトル(Dn)は 構造特性(つまり大気パラメタ―)の一次結合から得られる。これは単純でより 正確な決定ツリーへとつながるのである。 DEGAS アルゴリズム DEGAS = DEcision tree alGorithm for AStrophysics アルゴリズムは k - 次 オブリーク決定ツリーで、簡単なモデルが Bijaoui et al 2010 で紹介されている。 認識規則は以下の通り。 (1)ピクセル当たり平均フラックスのベクトル M を計算。 (2)分岐点における各スペクトル Sj に対し、内積 cj = Sj を計算。⟨c⟩ = cj の中間値。 (3)Sj を二つのグループ T1, T2 に分ける。基準は T1: cj ≤ ⟨c⟩ T2: cj ≥ ⟨c⟩ (4)平均ベクトル M1, M2 を各グループで計算し、 差ベクトル D = M1 - M2 を決める。 (5)ホイヘンスの定理によると、T1 と T2 が最も良く 分離するのは、M1 と M2 の周辺の分散が最少、つまり、 M と D が平行の時である。 (6) |
??? これは全然分からない。 |
3.1.訓練用分光データの用意[α/H] - [M/H] 関係人工スペクトルは表1のパラメタ―で MARCS モデルと Turbospec コードで 計算した。メタル量と α元素量との関係は以下のように仮定した。
観測スペクトル FLAMES の LR8 セットアップなので、 8400 - 8820 A が観測スペクトルである。 それに合うように、(計算、多分)スペクトルは 0.4 A サンプリングの 957 ピクセル になった。 3.2.ラインリストVALDVALD データベースから原子線リストを得た。 3.3.テストセット内挿スペクトルM-個のパラメタ― θ0m (m = 1 - M) を持つ人工スペクトル S0(k) (k = 1,K は波長) を内挿で導くことを考える。 このパラ メタ―は参照スペクトルのグリッド点の間にある。グリッド点のパラメタ―を θm (m = 1 - M)、スペクトルを S(k) とする。m-種パラメタ― の特性ベクトル(スペクトル)を Bm(k) とする。すると、 S0(k) - S(k) = Σm = 1,M (θ0m - θm)Σn = 1,M T-1m,nBn(k) (6) ここに、Tm,n は特性ベクトルの相関行列である。 Tm,n = Σk = 1,KBm(k) Bn(k) ( なぜこの式になるか、分からない。多成分解析で考えると、ある星のスペクトル S(k) を 特性ベクトル Bn(k) へ射影すると、星パラメタ― θn が得られる。 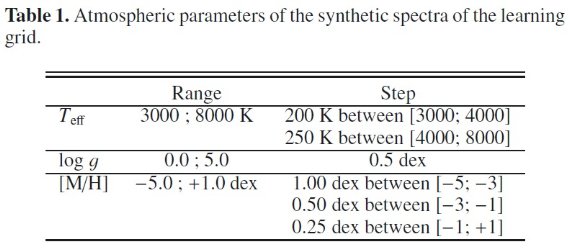 表1.訓練グリッド用大気のパラメタ― |
だから、単純には座標軸の変換のように考えて、 S(k) = Σm = 1,MθmBm(k) S0(k) - S(k) = Σm = 1,M (θ0m - θm)Bm(k) となる。Bm(k)が直交してないことを考えると上の式のようになるのか?) ブザンソンモデルを使ったテスト Robin, Reyle, Derriere, Picaud 2003 の銀河系ブザンソンモデルから、視線方向に沿った模擬星カタログを取り出した。 ウェブサイトから、銀河系バルジ、北銀極、中間星域 (l = 245, b = 45) 方向 から 104 の模擬サンプル星を取り出した。図2がそれである。 テストのため、その各星に対し、ブザンソンモデルのメタル量と、それより 0.75 dex 低メタルにしたサンプルを用意した。 http://model.obs-besancon.fr/ この 2 × 104 個の模擬星スペクトルを式(6)を用いて FLAMES LR8 分解能で内挿で得る。 (しかし、結局3個のパラメタ―に対応した 3個の特性スペクトルの線形結合で4 万個のスペクトルを表すわけか。単純に 近接パラメタ―グリッド点数個で内挿した方がよさそうだが、そうしない深い 理由があるのかな? ) 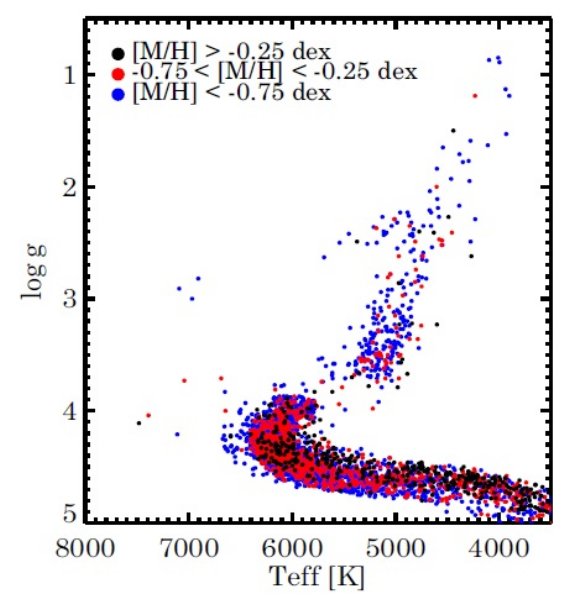 図2.テストセットへの入力パラメタ―。スペクトルはブザンソン銀河系モデル のウェブサイトから要請される模擬星カタログに基づいて計算された。 |
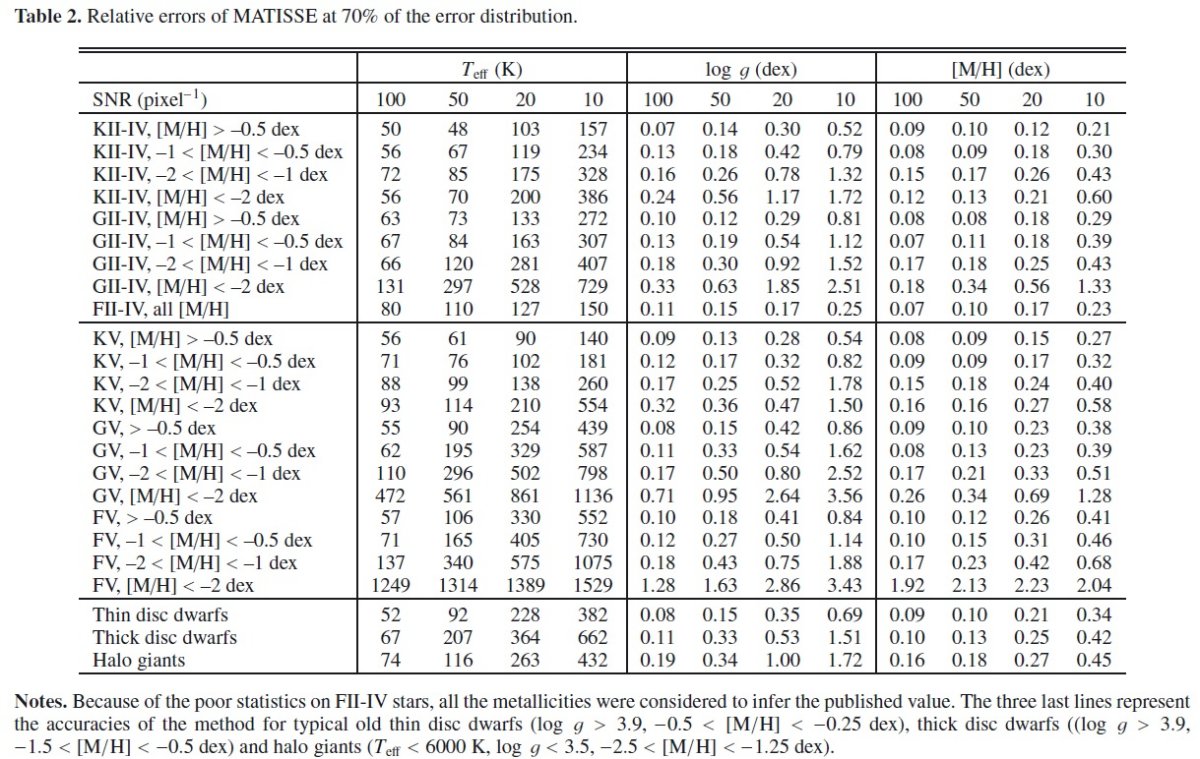
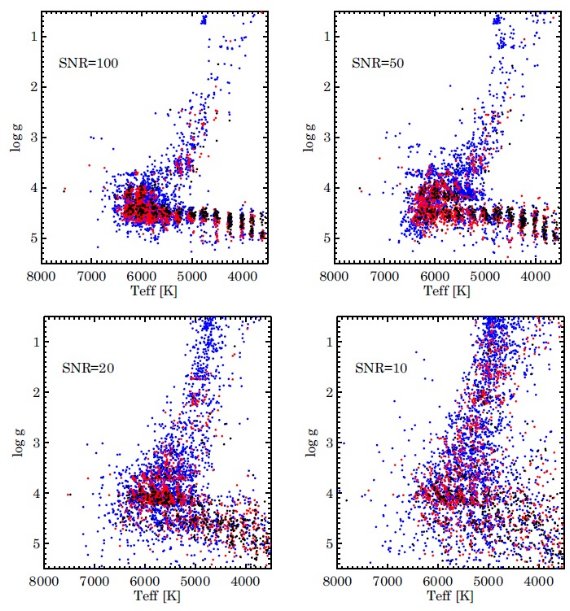 図3.MATISSE 法によるスペクトル解析の結果を HR 図で示す。カラーの意味は図2と同じ。低メタル の星は吸収線情報が少なく分散が大きくなる。 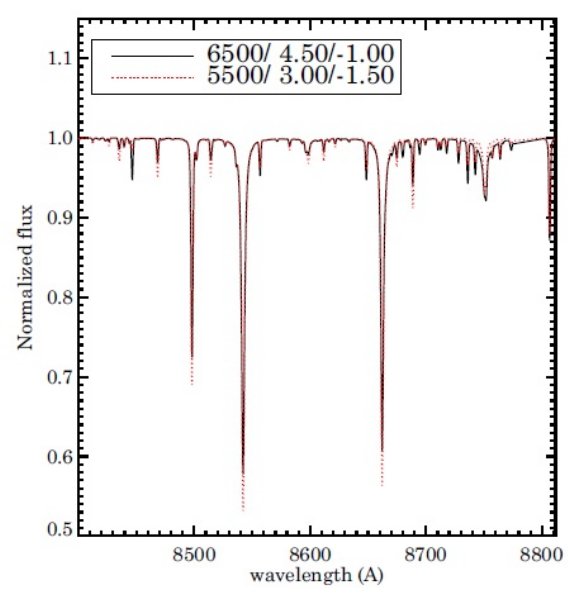 図5.ノイズなしの人工スペクトルによる縮退の例。黒=高温矮星。赤=低温巨星。 二つのスペクトルが異なるのは強いラインのコアと Pa12(8750 A) であるが、ウィング 部は殆ど同じ。 |
MATISSE 法の解析結果 S/N 比 = 10, 20, 50, 100 の 4 種類の計 8 万人工スペクトルを MATISSE 法で 解析した。図3は H-R 図の形が S/N 比でどう変わるか示す。表2は分布 70 % での エラー値の大きさを示す。図4の左側列が TISSE 法のエラーである。 MATISSE 法のエラーの特徴 (1)高メタル矮星では S/N = 20 まで良い結果が得られる。低メタルになるとエラーが 増加する。 (2)縮退領域が二つある。 Teff > 6000 の準矮星と巨星枝の間では Teff と log g の間で似たスペクトル特徴が共有される。もう一つは低温の準矮星に関して log g が よく決まらないという問題である。 二つの縮退は主に Ca II 三重線の振る舞い方に原因がある。であとごちゃごちゃは略。 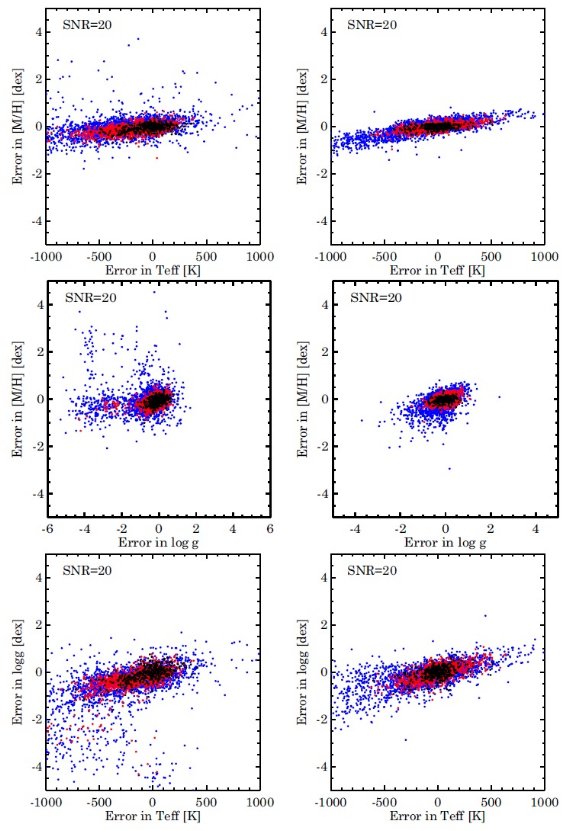 図6.左: MATISSE と 右:DEGAS S/N = 20 でのエラー相関。色の意味は図2 と同じ。 |
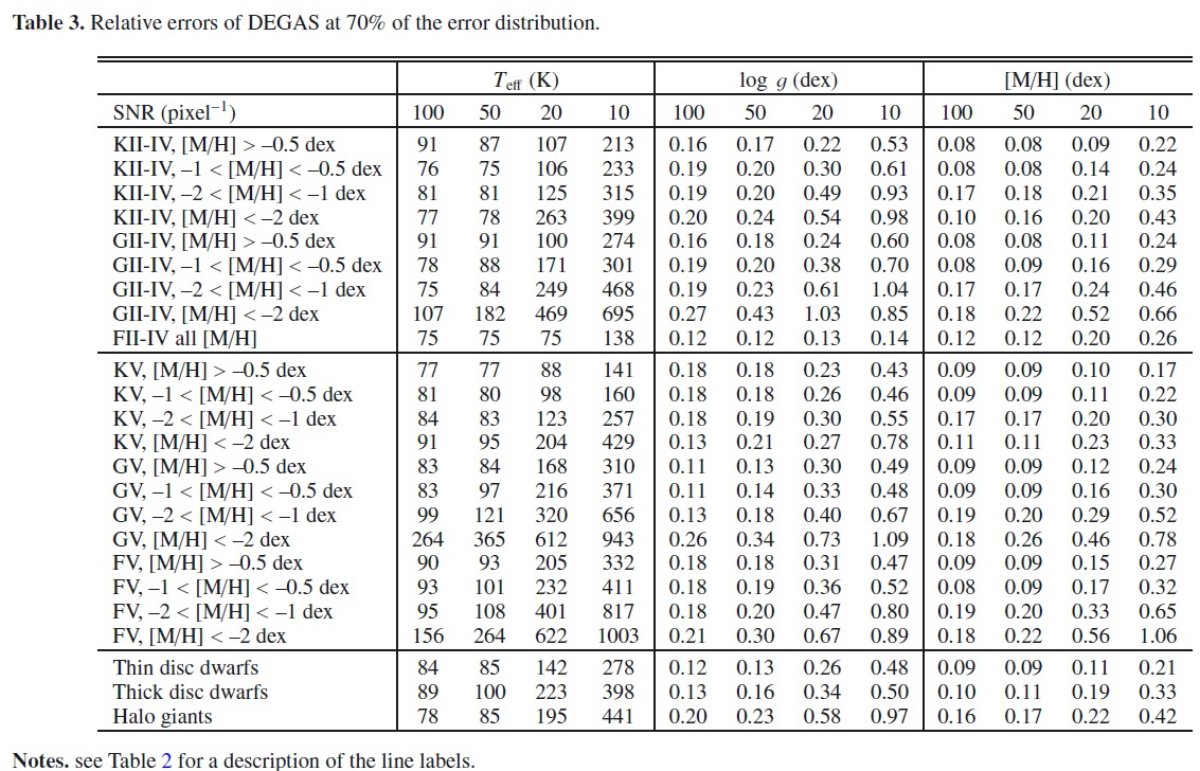
|
低 S/N に強い MATISSE が局所的な B(k) を用いるのに対し、DEGAS 法はパラメタ―空間を 全体的に眺める。そのため、局所的極小のわなにはまりにくい。それは、 S/N 比 が悪くなってもパラメタ―精度はそれほど落ちないことを意味する。S/N = 35 より 上では MATISSE, 下では DEGAS が良い結果を生む。 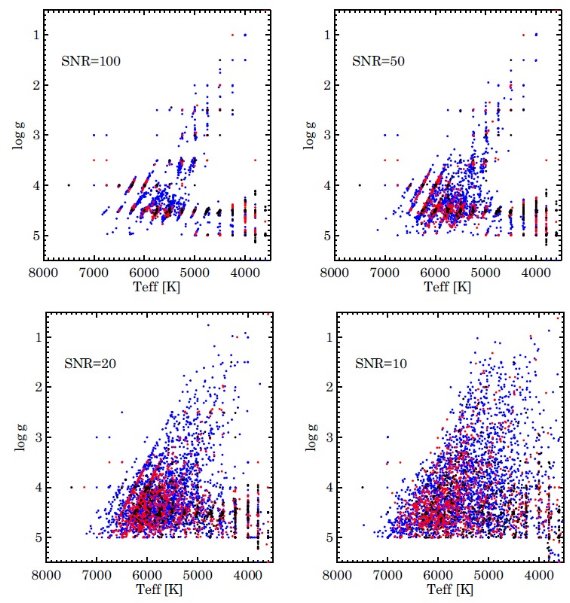 図7.DEGAS 法によるスペクトル解析の結果を HR 図で示す。カラーの意味は図3と同じ。 |
4.3.視線速度により生み出されるエラー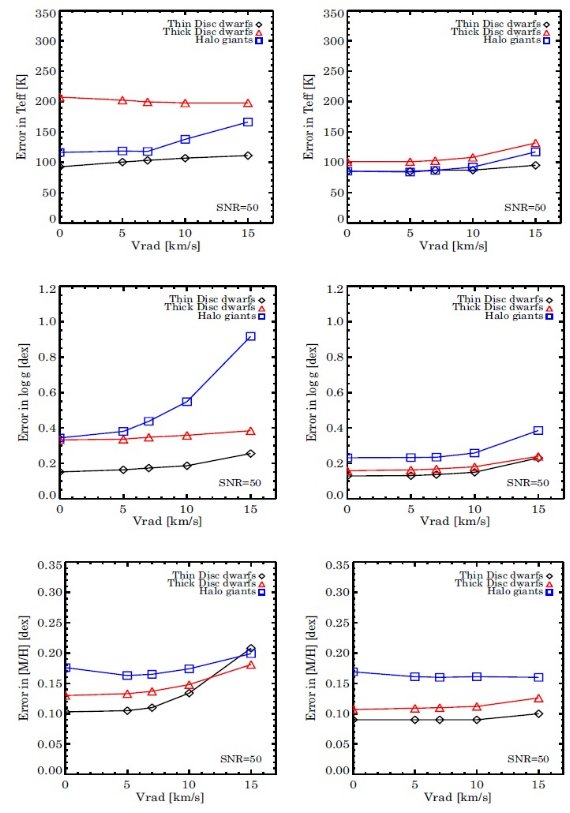 図8.視線速度とエラーの関係 |
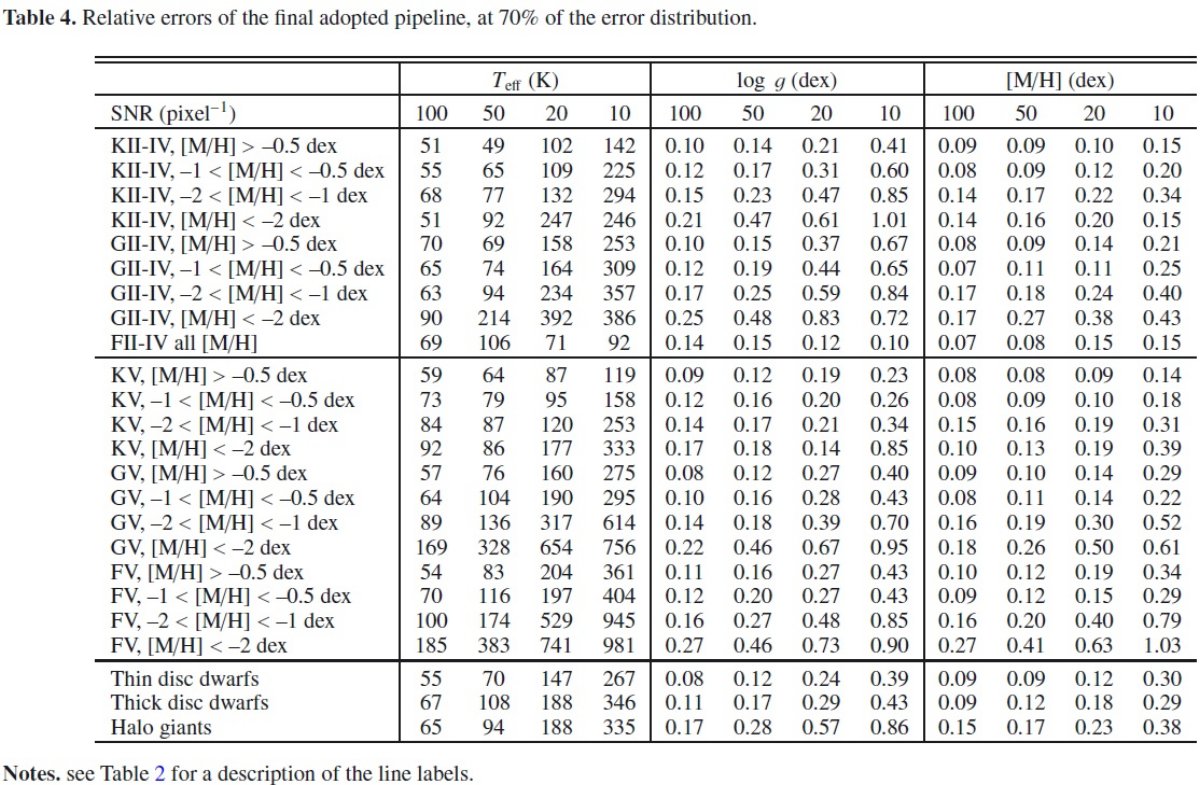
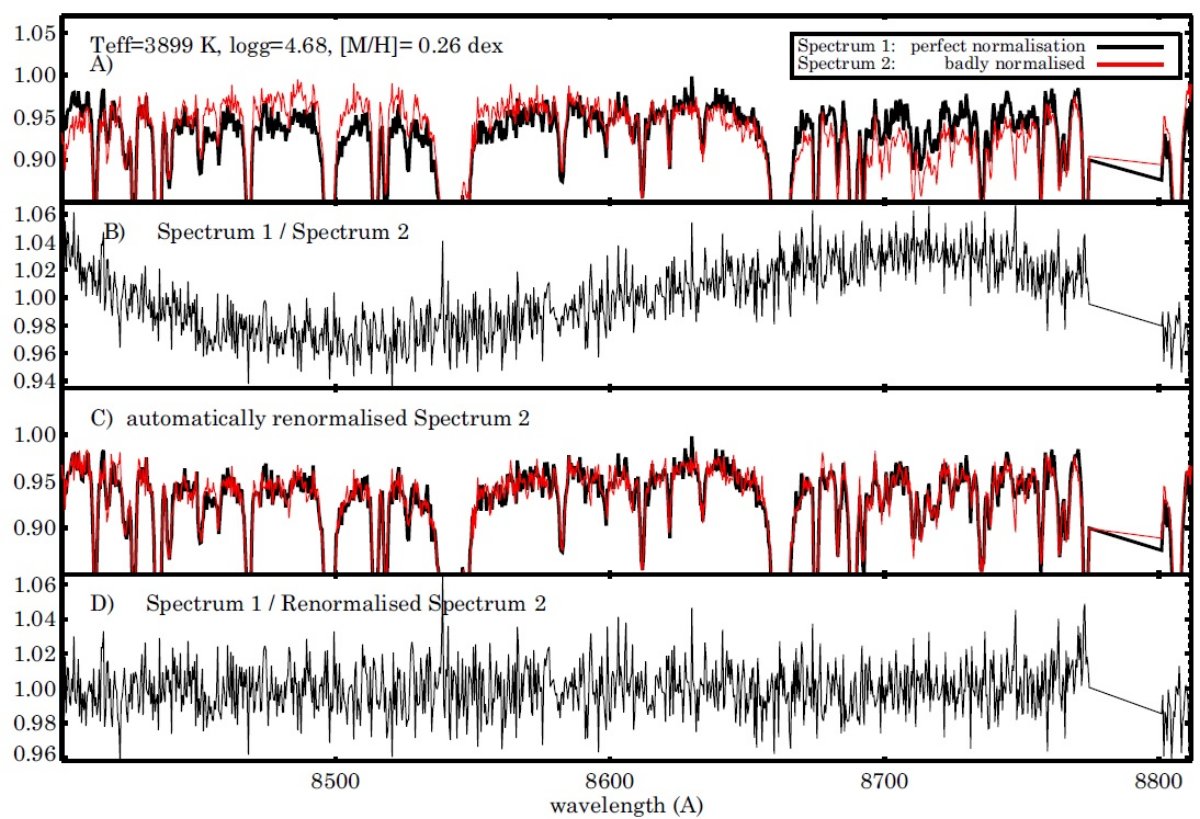
|
観測スペクトルデータベース 対象とする波長域で、高精度スペクトルのデータベースは二つしかない。 (1)S4N Allende Prieto et al 2004。近傍 118 星のサーベイ。 大部分は高メタル矮星。3620 - 9210 A, R = 50,000, S/N > 200. しかし、 我々の波長帯に回折次数のギャップが引っ掛からない星は 68 星であった。 (2)CFLIB Valdes et al 2004。900 高 S/N スペクトル。 3460 - 9464 A. Δλ = 1.2 A. HR-図全体をカバーしている。 メタル量は [M/H] = -2.5 dex まで。ただ、カタログのパラメタ―は幾つかの 独立な研究結果からの寄せ集めである。 これらのスペクトルを均して本論文で扱う分解能に変換し、前述のパイプラインを 通した。 S4N との比較 表5に、パイプラインで導いたパラメタ―とデータベースのパラメタ―との 系統誤差と分散を載せた。S4N との差は、ΔTeff = -108, Δlog g = -0.21dex, Δ[M/H] = -0.08dex, である。許容範囲ではあるが、 無視できるほどではない。注意しておくと、我々の波長域=GAIA RVS 帯データのみを 使った解析結果、Allende-Prieto 2008, は我々のパイプライン値と一致する。 CFLIB データ CFLIB 星のカタログパラメタ―は色々な論文の寄せ集めなので、PASTEL の最新 パラメタ―を使用した。その際、最低観測が二つ以上、[M/H] < -1 という条件 をつけた。図11に 162 CFLIB 星とパイプライン値との比較を示す。今回は系統的 なズレを見られなかった。 |
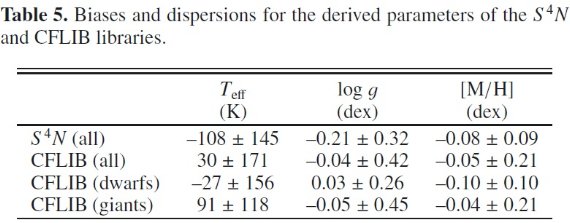 表5.S4N, CFLIB のパラメタ― |
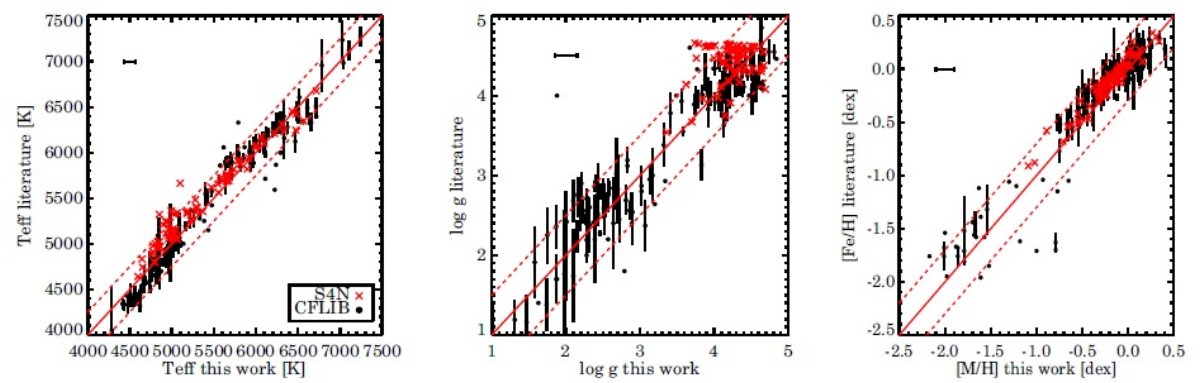
|
他の波長域、新しいパラメタ― 今回は GAIA を考慮して 8500 A 周辺スペクトルを扱った。しかし、同じ手法は 他波長域に容易に拡張できる。また、[α/Fe] を第4次元のパラメタ―として 加えることも可能である。 |