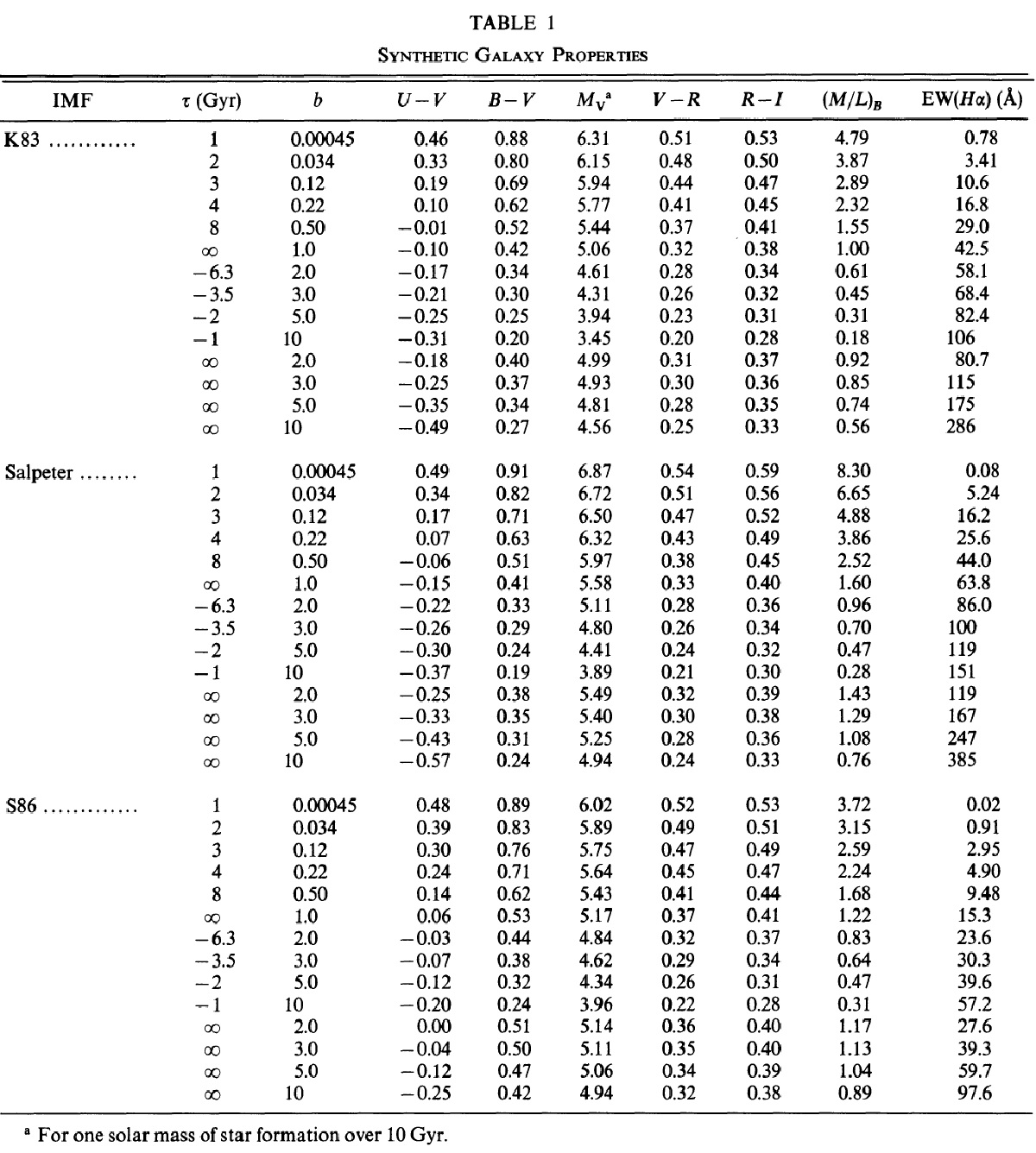
| Sa - Irr 銀河 210 個の Hα, UBV 観測を合成測光モデルと組み合わ せて、円盤銀河の過去と未来の星形成タイムスケールを再解析した。円盤銀河 の光電離率とカラーは Scalo の IMF と較べて大質量星が 2 - 3 倍多い IMF に最もよくフィットする。渦状銀河の表面輝度を用いて、バルジと無関係に その星形成史を調べた。現在の星形成率と過去の平均星形成率との比 b は Sa での 0.01 から Sc - Irr の 1 まで変化する。 |
ハッブル系列に沿って渦状銀河の測光特性の変化は基本的に星形成史の違い
に依るのであり、バルジ/円盤比の変化の効果は二次的であることが確認された。
現在の星形成率とガス質量を比較すると、ガス消費時間のメディアンは 3 Gyr
である。しかし、星からのガス還流を適切に扱うと、円盤のガス寿命を 1.5 - 4
倍伸ばす。その結果、多くの(全部ではない)円盤銀河での現在の星形成率は
ハッブル時間程度の期間維持され得る。
平均星形成率は現在の星質量と思えば、b は UV/OptNIR を表すから前半は当たり前 である。後半は前半と無関係にガス還流モデルだが、サンプル銀河をモデルに フィットするわけでもない。どうも様々な結果は星形成効率の違いで生じるらしい が、それを顕わに示さない。効率が変わる原因も論じず、最後に未知パラメターと述べるのみ なのは不満 |
| 早期型銀河(S0-Sb) はハッブル時間よりずっと短い時間に 星形成によりガスを消費しきったが、晩期型(Sc-Irr) は現在まで ほぼ一定の星形成率を維持している。しかし、円盤とバルジを一緒に 測光して解析すると不明瞭な結果があられる。円盤だけを調べると 皆同じ星形成史を示すという研究もある。もう一つの問題は IMF の変化の役割である。IMF を極端に変えれば、銀河の測光学的性質 を全て説明できるという説 Larson86 さえある。 | おそらく、これまでの研究で最大の謎は、ガス消費時間の短さである。 Roberts86 はガス欠乏時間を総合的に調べ、ハッブル時間より長い とした。その後、それが数 Gyr であることが明らかになった。 Pfenniger93 は晩期型銀河の星形成を維持するには大量のガス降着が 必要であるとした。ガスのリサイクルの重要性を指摘する研究 Truran71, Ostriker75 はあるが、銀河の星形成の性質は通常即時 リサイクル近似で解釈されている。 |
| 主データは Hα+[NII] で、[NII]/Hα = 0.5 を仮定する。 | 全サンプルは 210 銀河からなる。 |

3.1.モデル計算法恒星進化モデル星の進化は Schaller93 を用いた。0.8 - 2 Mo 星の進化はヘリウムフラッ シュで終わる。大気モデルには Kurucz 1992 を使用し、それから 大質量星の寿命期間内に放出される電離フォトンの総数を計算した。IMF と組み合わせると、星形成単位質量当たりの電離フォトン数が決まる。 それに対応する Hα 光度も計算される。 IMF 多くの IMF が ψ(m) = amΓ d(log m) の形で 表現される。Salpeter55 は Γ = -1.5 である。 Miller,Scalo79 では、Γ=-0.4(0.1-1 Mo), -1.5(1-10 Mo), -2.3(10-100 Mo). Scalo86 では数値の表の形で与えられている。 SFH 通常、星形成率を以下の形で与える。 R(t) = Ro exp(-t/τ) (1) Scalo86 の誕生率パラメター b = SFR(現在)/⟨SFR⟩ として、 b ≤ 1 は減衰型または一定星形成史に対応。b > 1 の銀河を 増大指数関数で表すのは無理がある。それは、一定星形成 b = 1 の上 にバーストが載るモデルで表す。表1、図1には b とカラーの関係を示す。 |
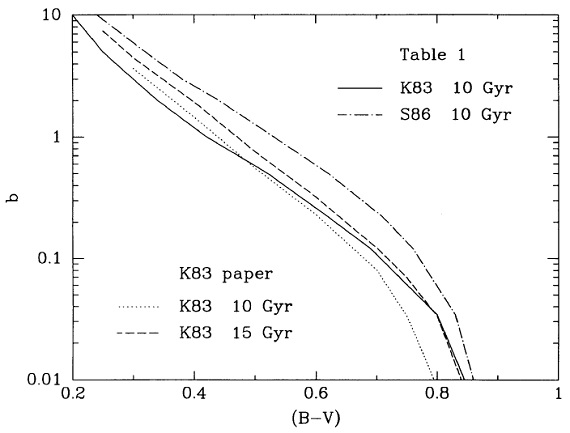 図1.Scalo 星形成パラメター b と B-V カラーの関係。 3.2.電離性質SFR を決めるパラメターは電離フォトン光度(Hα光度)の 総星質量に対する比である。表2にそれを載せる。 |
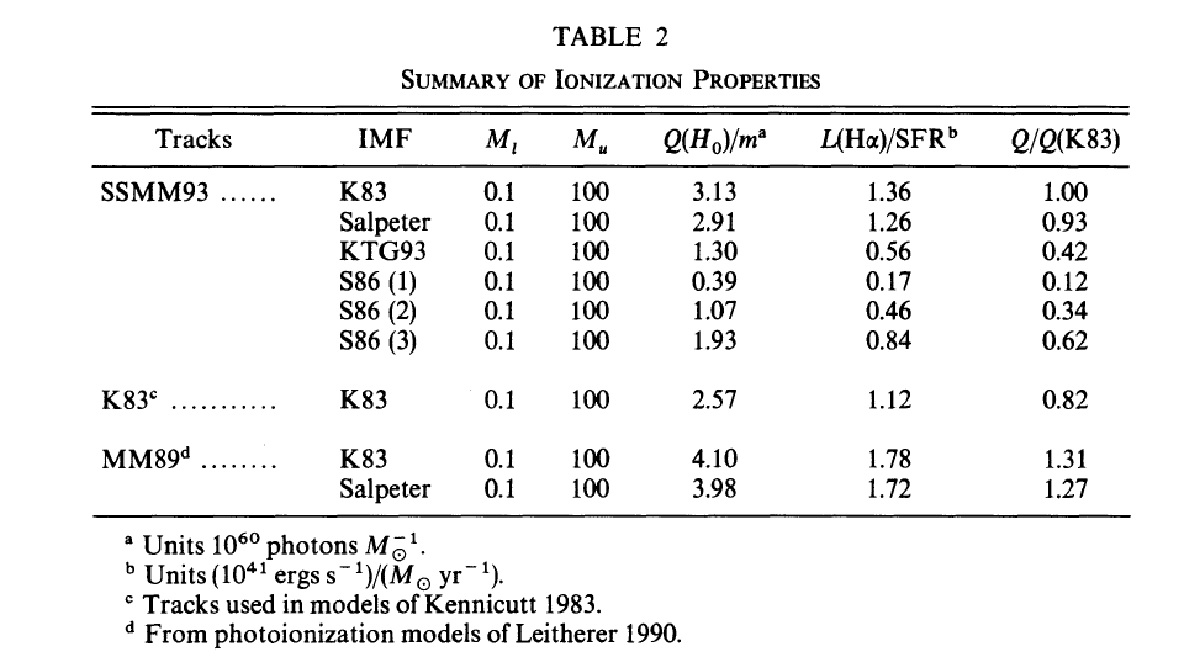
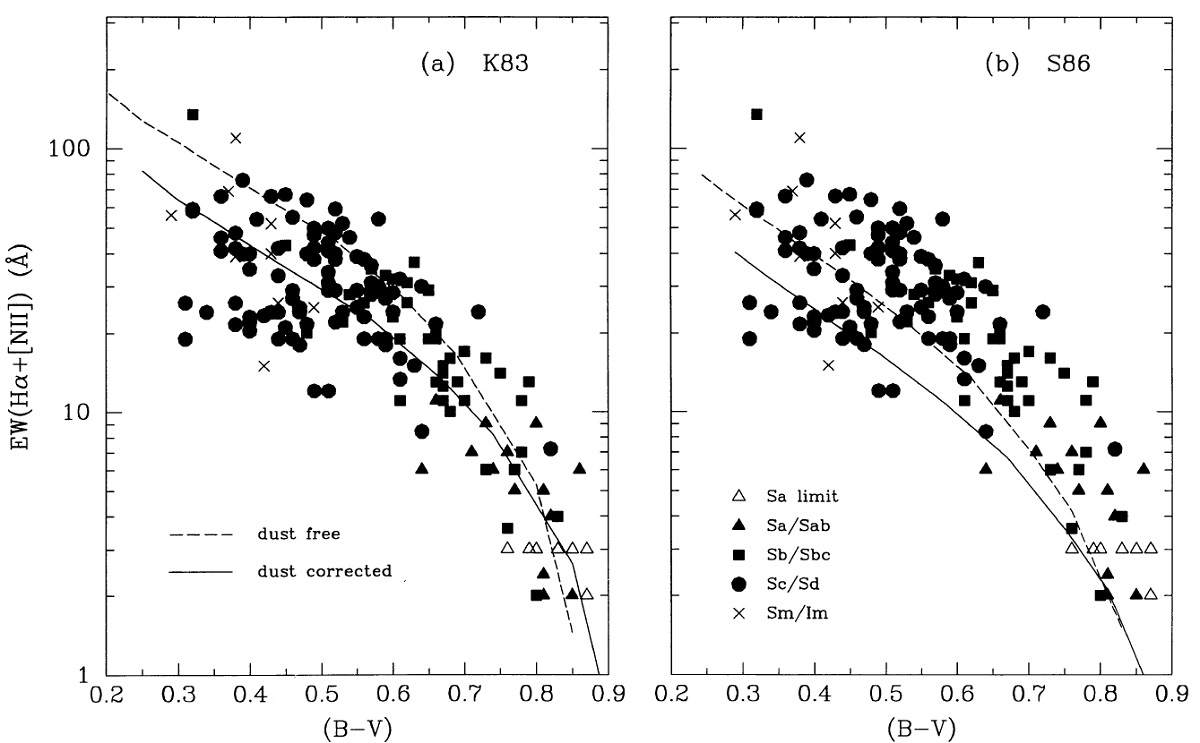
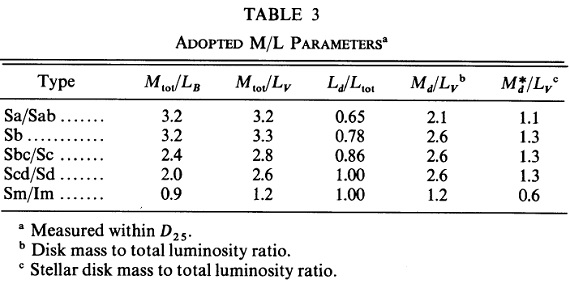 表3.採用した M/L パラメター |
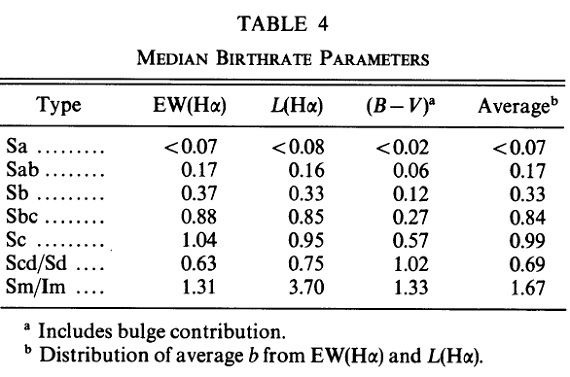 表4.メディアン星形成パラメター 5.1.星形成パラメター b の決定Kennicutt83 では 116 銀河に関して、Hα から求めた SFRs と円盤の 年齢と質量からの平均 SFRs の二つとから銀河形成パラメター b を決めた。 b = SFR/⟨SFR⟩ = SFR*&taud*(1-R)/Mdここに、&taud=円盤年齢。Md=星総質量。R=マスロスで失われた割合。この方法は観測量を使っていて確実性が高い。ただし、 円盤の星質量は L の観測値と銀河のタイプごとの平均 M/L とから間接的に 決めるのが欠点である。 |
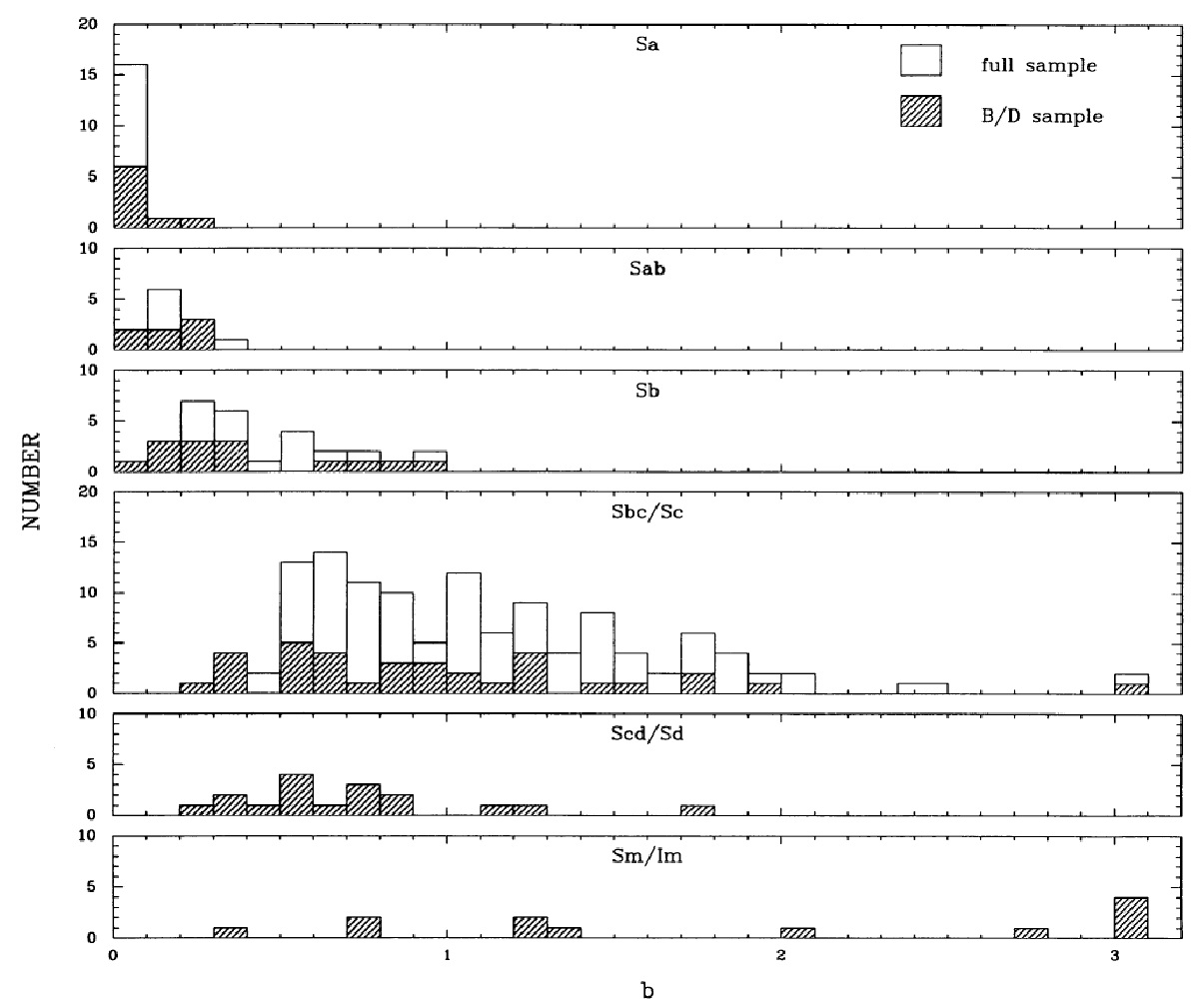
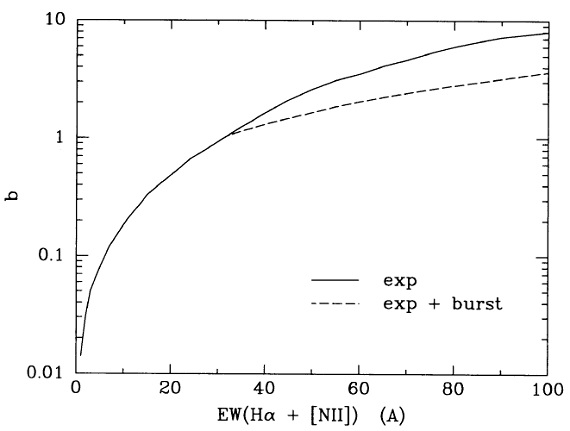 図3.Scalo 誕生率パラメター b と Hα 輝線等値幅の関係 表2から採った。実線=指数関数SFH.破線=指数関数+バースト 5.2.結果表4と図6 に b の分布を示す。ハッブルタイプと共に星形成史が順次変化 する。Sa 円盤は b = 0.01 - 0.1, Sc では b = 0.5 - 2 である。これは昔か ら言われている積分カラーと Hα フラックスのハッブル系列に沿った変 化と整合する。 |
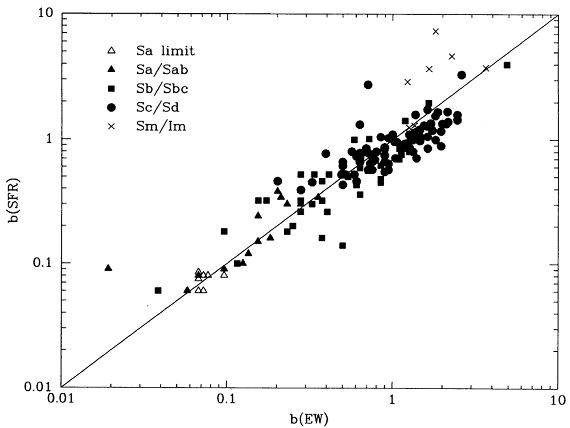 図4.b(SFR) と b(EW) との比較。 b(EW) = モデルの EW(Hα)対 b 関係を使い、観測 EW から求める。 b(SFR) = 現在の SFR 観測値と銀河星質量(過去の星形成の累積)から求める。 |
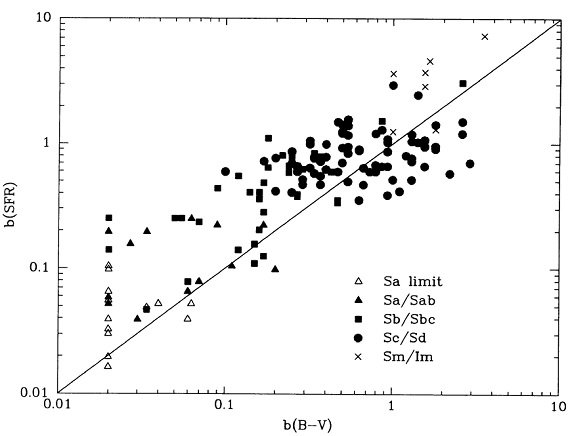 図5.b(SFR) と b(B-V) との比較。 b(B-V) = モデルのカラー対 b 関係を使い、観測カラーから得る . b(SFR) = 現在の SFR 観測値と銀河星質量(過去の星形成の累積)から求める。 |
5.3.議論閉じた箱モデルでの説明Sa 円盤ではなぜ Sc 円盤の 1/10 の時間スケールで星形成が完了してしま ったのか?初期状態で Sa のガス密度が高かったことが、原因と考えたくなる。 しかし、もしそうなら Sa 銀河の星表面密度は Sc より高いはずであるが、観測 では確認されていない。 |
星形成の密度閾値 解答には何か追加の機構が必要である。例えば、星形成には密度閾値が存在する というアイデアがある。ガス密度がジーンズ密度付近まで下がると星形成が突然 停止するというモデルである。その結果、初期状態の僅かな違いが最終状態では 大きな差となる。 降着ガス 他の可能性は、ガスの降着により円盤が形成されてきたとするモデルである。 このモデルでは、星形成史は実はガス降着史をなぞっているのである。 |
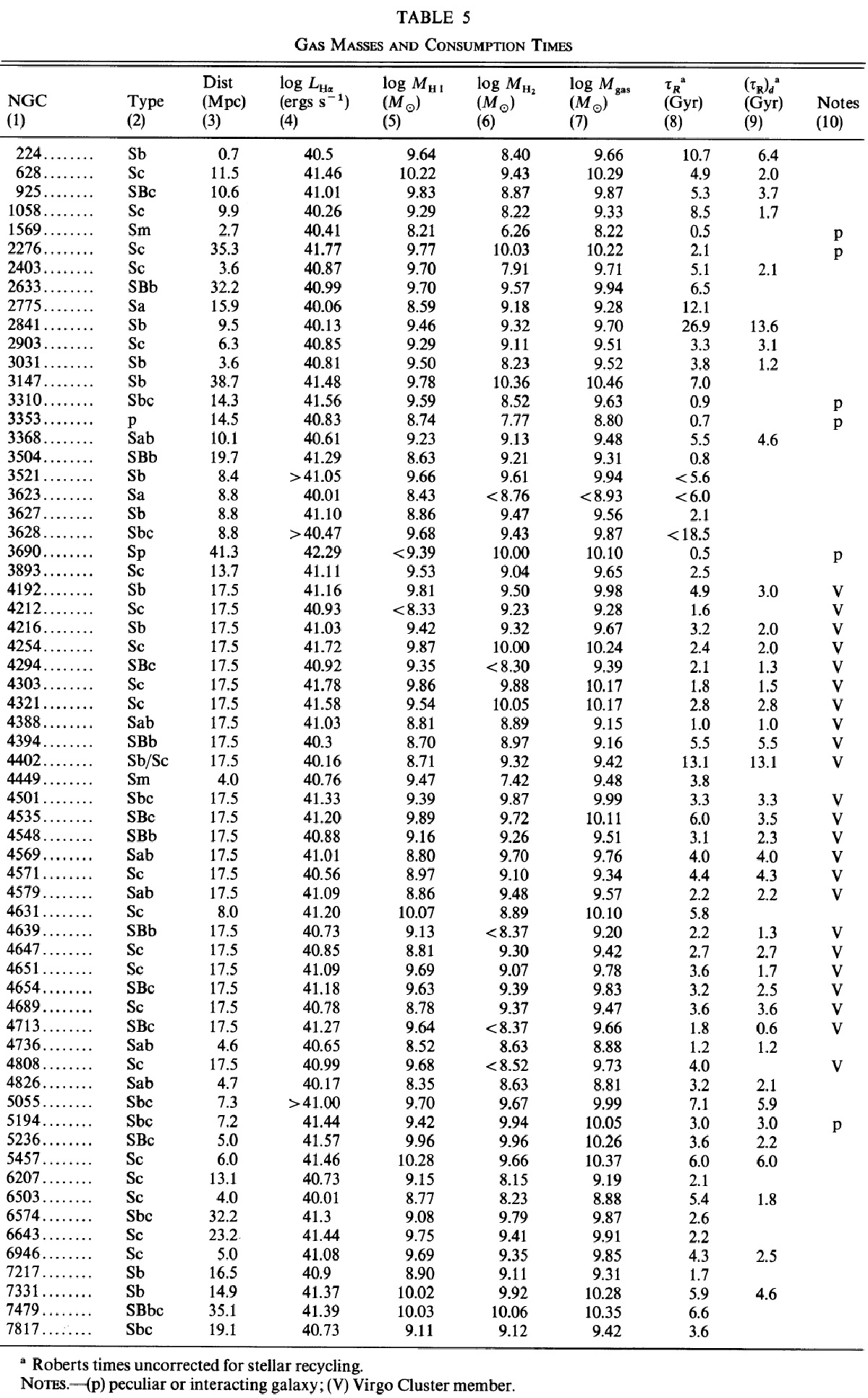
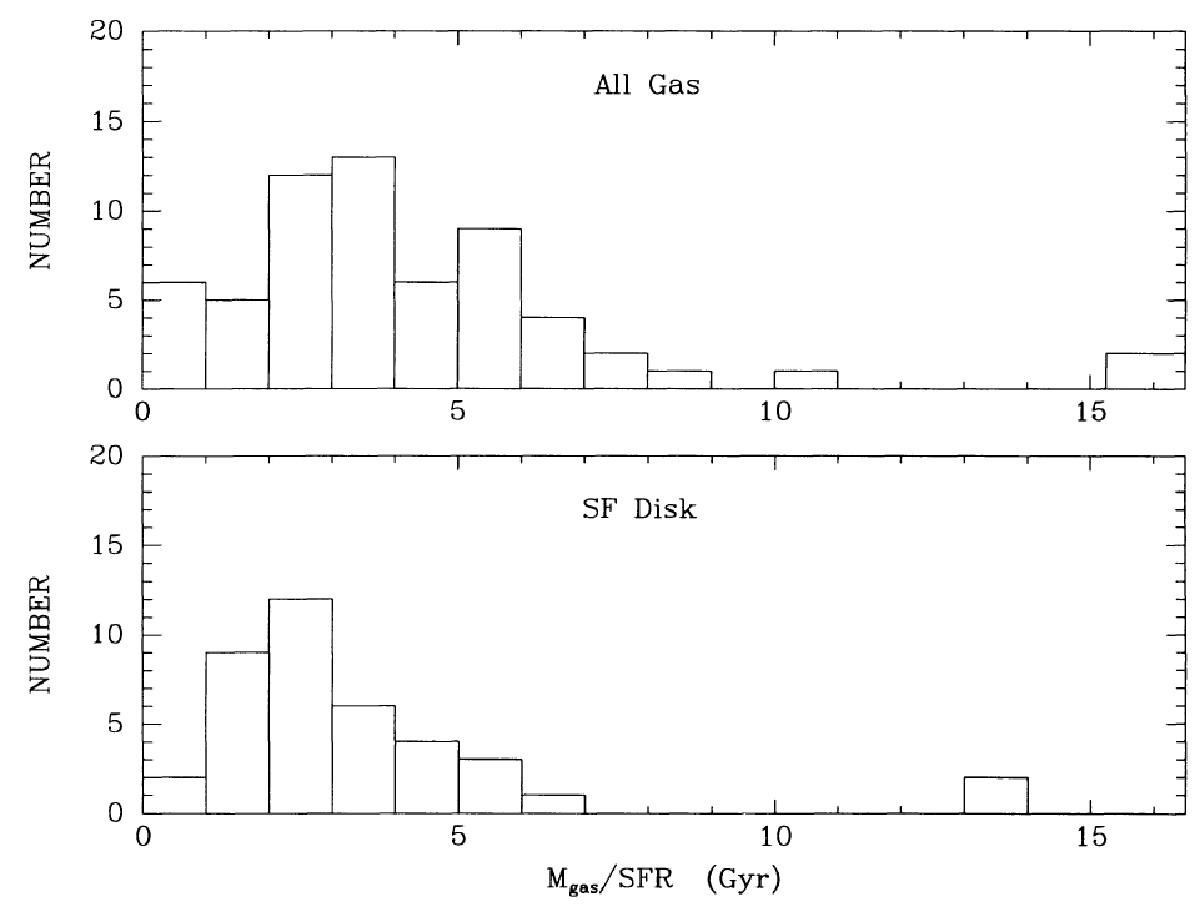
6.1.ロバート時間の分布Roberts time τRロバーツ時間 τR は τR = Mgas/SFR で定義される。ガス消滅の実際の時間スケールは、星からのリサイクルや将来の SFH に依存する。これまで大部分の研究ではリサイクルが無視されるか、Tinsley80 に従って 25 % の補正で済ませるかであった。 銀河全体のロバート時間 ガス質量は HI, CO 観測から求めた。質量と SFR は距離依存があるが、ロバ ート時間にはないことに注意せよ。表5にそれらの値を載せる。図7a には ロバート時間の分布を図示する。そのメディアン値は 3.6 Gyr である。これは Larson80, Kennicutt83 が得た 4 - 5 Gyr とだいたい等しい。主な違いは SFRs の推定がよくなったことと、CO 観測が加わったことである。 |
可視円盤のロバート時間 ロバート時間の評価の際には全てのガスが星形成に使用されると仮定して いる。しかし、実際には HI の多くは星形成円盤のはるか外側に位置する。その 結果、内側円盤においてはガス消費時間は銀河全体のロバート時間よりずっと 短い。図7b にそれらを示す。メディアンは 2.7 Gyr となる。 消費時間パラドックス 図7はリサイクルなしでは、近傍渦状銀河の大部分で星形成円盤のガスは ハッブル時間の 0.1 - 0.6、平均すると 1/4 以下, で消費され尽くすことを示す。 星形成に必要なガス密度閾値を考えると、これらの値でさえも過大である。と いうのはガス密度がその値以下になると星形成が止まってしまうからである。 Kennicutt89 はそれが現在のガス密度の約半分であろうと見積もった。その場合、 Sc 銀河は 2 Gyr 以下の間に Sa - Sb に変わる。 |
5.2.リサイクルモデルinstantaneous recycling approximation円盤進化モデルの大部分は即時帰還近似(instantaneous recycling approximation) を採用している。Larson80, Kennicutt83 では Tinsley80 に倣って、帰還率= 0.2 を採用した。今から考えるとこの値は小さ過ぎた。1980 以降の恒星進化 モデルと初期質量関数 IMF の改訂の結果、R の大幅な増加が必要となった。 delayed mass loss 以上に加え、低質量星からの遅延マスロスによるガス消費時間伸長効果は、 即時帰還近似を著しく上回る。Ostriker, Thuan 1975 は銀河円盤の場合に それを示した。ここでは新しい星パラメターを用いて遅延マスロスの効果を 調べる。 SSPモデルの入力パラメター まず SSP に対するマス帰還の時間変化を調べる。必要な入力は、 初期最終質量関係((IFMR) 星質量寿命関数 初期質量関数(IMF) である。ここでは 1 ^ 8 Mo 星に対し Weidemann 1987 の IFMR を使う。この 範囲の星は最後に 0.55 - 1.55 Mo の WD を残す。帰還率は 55 - 81 % である。 円盤年齢 10 Gyr を仮定しているので、1 Mo 以下の星はマスロスを行うまでに 進化しない。一方 8 - 100 Mo の星は 1.4 Mo の残留天体を残し、残りが帰還 ガスとなる。Arnett 1978. M > 25 Mo ではもっと重いブラックホールが 残る可能性はあるが、この質量帯の総質量は無視可能なほどに小さい。星の 寿命は Schaller93 の太陽メタル星進化モデルから採った。 IMF は (1) Kennicutt83 (Γ=-0.4 for 0.1 - 1 Mo, Γ = -1.5 for 1 - 100 Mo), (2) Salpeter55, (3) Scalo86, (4) Kroupa93 SSP 帰還率を時間ステップ 1 Gyr で計算した。第1ステップだけは 0.2 Gyr ステップで計算した。 |
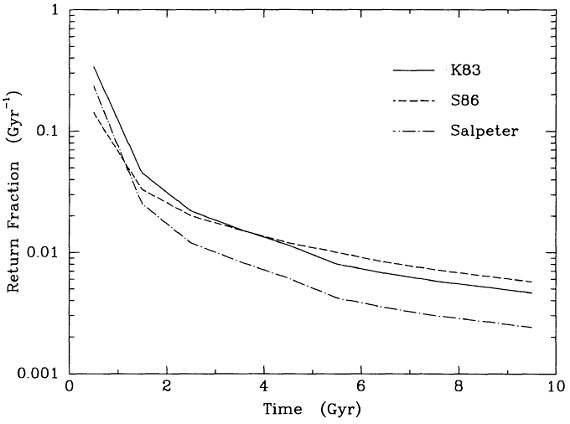 図8.単一星種族に対する、星質量の帰還率の時間変化。帰還率は初期星総質 量で規格化している。第1時間ステップ = 0-1 Gyr での質量帰還の大部分は 最初の 200 Myr 内で起きる。 図8=帰還率時間変化 図8には帰還率の時間変化を示す。縦軸には 1 Gyr 間隔の間にナンパ^セ ントの質量が帰還するかを示している。どの IMF でも最初の 1 Gyr にかなりの マスロスが起きる。特に最初の 0.2 Gyr で半分以上が帰還する。 (0.2 Gyr は 3-4 Mo に相当 ) その後は帰還率 がゆっくりと低下していく。Scalo86 IMF は初期には少ない帰還率であるが、 4 Gyr を過ぎると比較された中では最高になる。 |
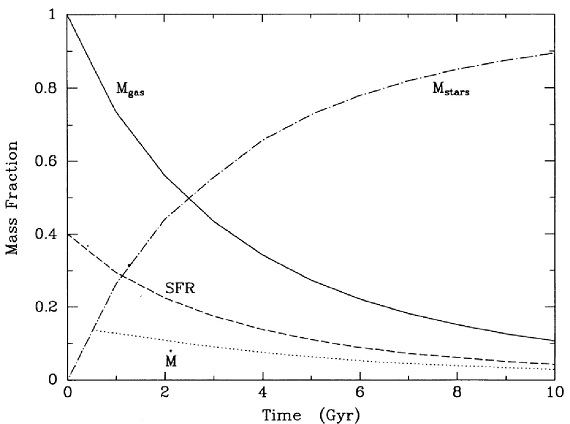 図9.Kennecutt83 IMF と星形成効率を 4 %/0.1 Gyr を仮定してのモデル。 ガスと星マスは円盤マス=1でで規格化。星形成率と還元率は 1 Gyr あたりの 質量比。 総還元率 4種類の IMF で総質量還元率は Larson80, Kennicutt83 で使われた Tinsley80 の 20 % よりはるかに高い。10 Gyr での還元率は Scalo 26 %, KTG93 で 30 %, Salpetrer 30 &, Kennecutt83 46 % となる。面白いのは Salpeter と Scalo86 は IMF の形が大きく離れているのに、還元率は 30 % で同じことである。両 者は 10 Gyr での総還元率は同じだが、図8に示されるように、時間変化は大 きく異なる。 モデルグリッド 円盤は時間ステップ 0.2 - 1 Gyr で星形成効率 1% - 50%/0.1 Gyr (シュ ミット線形則)で1層モデルを計算した。Kenecutt83 と Scalo86 IMF に対し て、円盤年齢 10 Gyr で計算を行った。 図9=進化の例 図9には、星形成効率 4 %/0.1Gyr の場合での典型的な例を示す。SFR は時 間と共にほぼリニアに低下していく。10 Gyr 後には円盤のガス比は 11 % に 低下する。最近 1 Gyr に作られた星の比率は 5 % である。この二つの量は Sb 銀河に典型的な量である。現在の星の比率は 89 % であるが、これまでに形成 された星の総量は 161 % である。 |
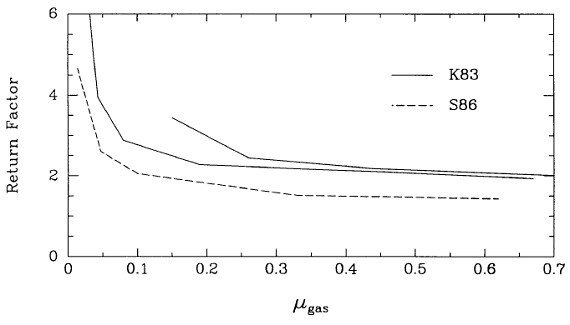 図10.リサイクルによるロバート時間への補正ファクター。実線=Kennecutt83 IMF。 破線=Scalo86 IMF. モデルは線形シュミット星形成率を仮定。ただし、一番上は自乗 型シュミット則。 再生ファクター(recycling factor) 図9のモデルでは、10 Gyr 後の現在還元されつつあるガスの比率は現在の星 形成率の 62 % である。したがって実質的なガスの減少率は, 星形成率に (1-0.62) を掛けたものになる。現在のロバート時間は 0.1/0.04 = 2.5 Gyr だが、実質ガス 減少時間は 2.5/(1-0.62) = 6.6 Gyr となる。つまり、dM/dt =還元率とすると、 再生ファクター = [1-(dM/dt)/SFR]-1 はロバート時間を伸長する数値である。 図10には3つのモデルに対して、ガス比率 μgas と再生ファクター との関係を示す。現在のガス比率が大きい、ゆっくり進化する銀河では再生フ ァクターは漸近値 (1-R)-1 に近づく。ここに R は全体還元値 で、 Kennecutt83 IMF では 46 %, Scalo86 IMF では 26 % である。しかし、もっと 急速に進化する円盤 b « 1, μgas « 1, では再生 ファクターはもっと大きくなる。なぜなら、古い星からの遅延マスロスが現在の SFR を上回るほどになるからである。 実際の銀河の再生ファクター 再生ファクターの決定は、IMF や SFH に依存するので簡単に決められない。 しかし、だいたい 1.5 - 4 の範囲である。これは表7の銀河の大部分で、現在 の星形成が今後 4 - 10 Gyr は続くことを意味する。 パラドックスの解消 以上の結果は、ガス消費時間がハッブル時間に比べ短すぎるというパラドッ クスを解消するものである。リサイクルファクター 2 - 3 で、近傍銀河の大部分 では星形成寿命がハッブル時間程度にまで伸びる。しかし、強調しなければならない のは、図7のいくつかの銀河では今後 2 - 3 Gyr の内に、ガス密度が星形成密度閾値 まで低下するであろう。図6に示すように、近傍にある多数の Sa - Sb 銀河では現在、 過去の平均星形成率に比べ非常に低い星形成活動レベルにある。晩期型銀河のいくつ かで早期型銀河への転換が進行中のはずである。 |
|
1.SFH の系統的な変化がハッブル系列を生む S - Irr のハッブル系列は SFH の系統的な変化が原因である。バルジ/円盤比は二次的な 効果しか持たない。 ( SFH の違いの原因は?) 2.太陽近傍 IMF は頭を欠く S - Irr のカラー系列は IMF の変化などを必要とせず、SFH の差で再現できた。 しかし、近傍銀河で観測される光電離光子数は Miller, Scalo (1979). Scalo86 の太陽近傍 IMF と較べ、大質量星数が 2- 3 倍必要である。太陽近傍 のサンプル星には大質量星が不足しているか、活発な星形成域では IMF がフィールド 異なるのかとも知れない。 3.赤外星形成爆発銀河 太陽近傍 IMF の予言よりも光電離光度が過大であるという問題は、赤外星形成爆発銀河 での超過と同じ方向である。我々のベストフィット IMF を使えば、例えば M 82 で低質 量星の足切りのような措置は必要ないかもしれない。 |
4.ガス消費時間 ガス還元率は依然考えられていた 20 % よりずっと大きい。それを考慮すると、 ガス消費時間は 5 - 15 Gyr となる。それでも幾つかの晩期型銀河ではガス 消費時間は数 Gyr となる。それらには現在爆発星形成を行っている銀河や 早期型銀河への門口にある晩期型銀河が含まれる。 未知のパラメター 単位光度当たりの星形成率はハッブル系列に沿って大きな変化を示す。それは 個々の銀河で動径に沿った SFH の変化より大きい。一方、ハッブル系列に 沿った平均表面密度の変化は、個々の円盤内での密度変化より小さい。 これらから、表面密度以外の他の未知のパラメターが円盤内の星形成率を決めている らしい。 |