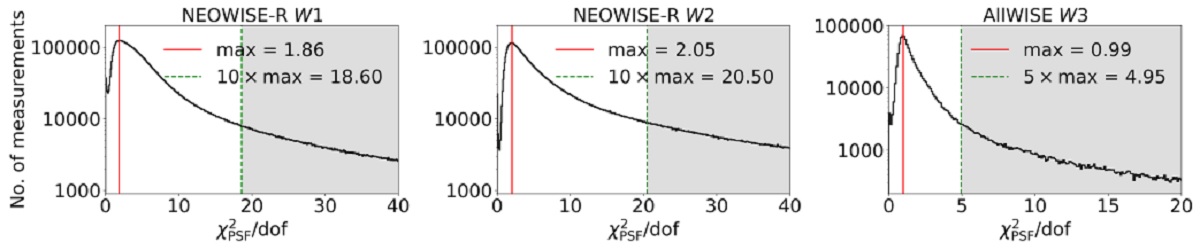
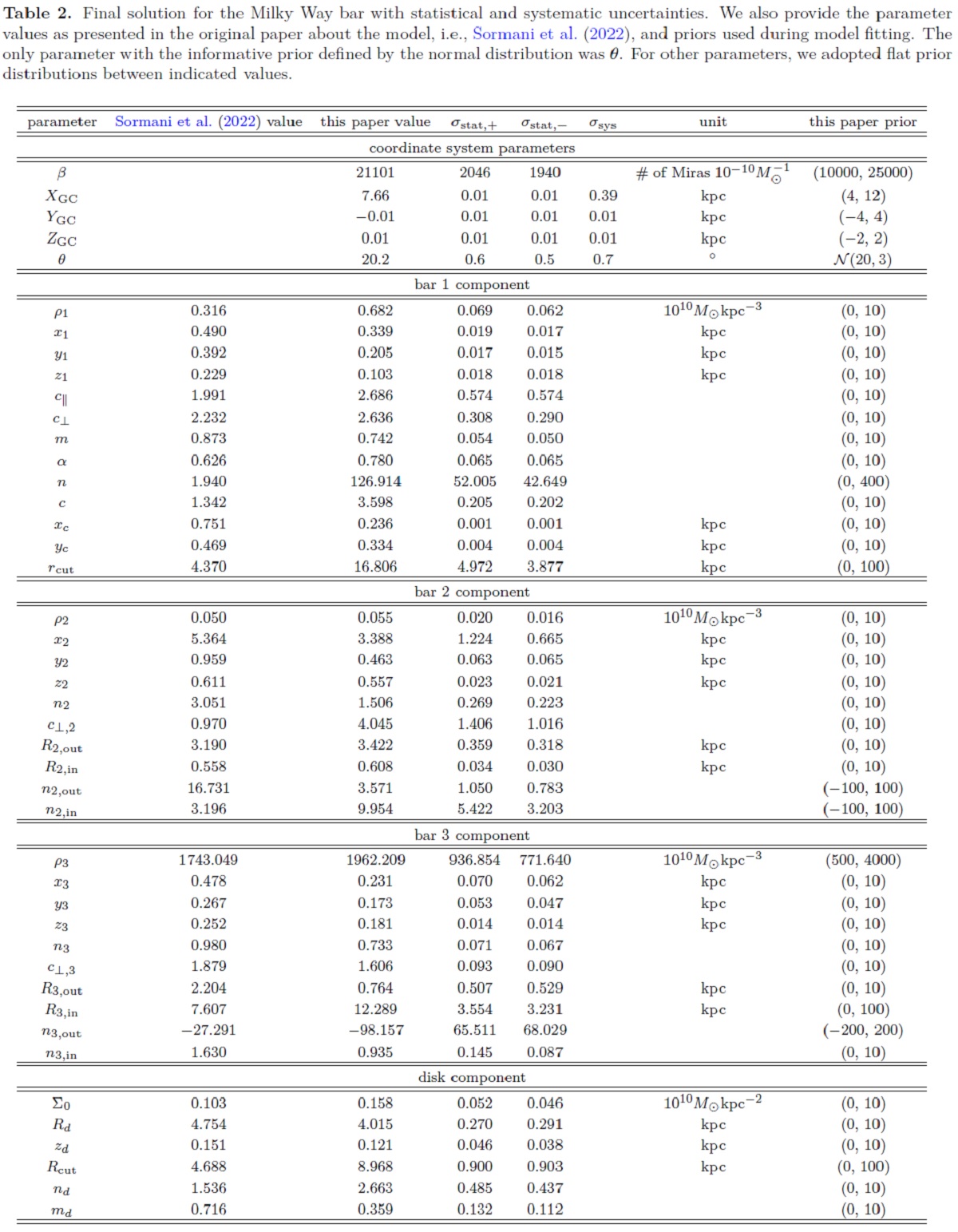
| OGLE で発見された 65,981 ミラ型星の空間分布を、 X−型ボックス成分を 含む3成分バーと非軸対称円盤から成るモデルで解析した。距離不定性は 階層的ベイズ推定法で考慮した。銀河中心までの 距離は Ro = 7.66 ±0.01(stat.)±0.39(sys.) kpc、 バルジ主軸と太陽-GC 視線方向との角度は 20.2°±0.7° である。 |
若い種族と中間年齢種族から成る銀河系の3次元マップを初めて提示する。
バルジの X-型成分とフレアリング円盤の独立な証拠も示す。ここに使用した
ミラ型星の完全なカタログも示した。距離精度中間値は 6.6 % である。
( 実際はバルジモデル ) |

3.1.中間赤外での平均等級と振幅W1, W2, W3 の平均等級W1, W2, W3 の平均等級は重み付きの平均フラックスを等級に直した。平均カラーは 平均等級の差で決めた。 3.2.星間減光補正減光マップ "mwdust" の利用 Bovy et al. (2016) の3次元減光マップ "mwdust" を使用する。これは (l, b), d, バンドを指定すると 減光量を与えてくれる。このマップは幾つかのマップを合成したもので、それらは Drimmel et al. (2003) Marshall et al. (2006) である。 |
Green et al 2019 と Skowron et al 2019a はVISTA 273 セファイドの
MIR, Ks 測光から得た減光を "mwdust" の値と比較して、その信頼度を調べた。
彼らは、個々星の Ks 測光に減光決定精度が強く依存するので "mwdust" の使
用の方がより信頼出来て一様な減光値を与える、と結論した。
減光曲線 A(Ks) から MIR 減光への変換には APOGEE から得た MIR 減光曲線 Xue et al 2016 を使用した。 |
|
LMC PLR Iwanek et al 2021 は LMC ミラの PLR を求めた。 減光と距離 個々のミラ星までの絶対等級を用いて、距離を WISE と Spitzer の各バン ドで求めた。見かけ等級、距離、減光が整合するように逐次近似を行った。 それらの距離から平均距離を計算した。 |
サチュレイション Spitzer の飽和限界は I1 で 6 mag, I2 で 5.5 mag, I3 で 3 mag, I4 で 3 mag である。WISE の飽和限界は W1 で 8 mag, W2 で 7 mag, W3 で 3.8 mag である。しかし、profile-fitting photometry を行うと 飽和限界は W1 で 2 mag, W2 で 0 mag, W3 で -3 mag まで上がる。 しかし、慎重を期して、W1=4, W2=3, W3=0 mag より明るい場合は距離決定から 外す。それらが 2172 ミラで起きた。 距離ありの星数 こうして 65,385 星の距離を求めた。59,902 星の距離精度は 10 % 以下である。 メディアンは 6.6 %. |
|
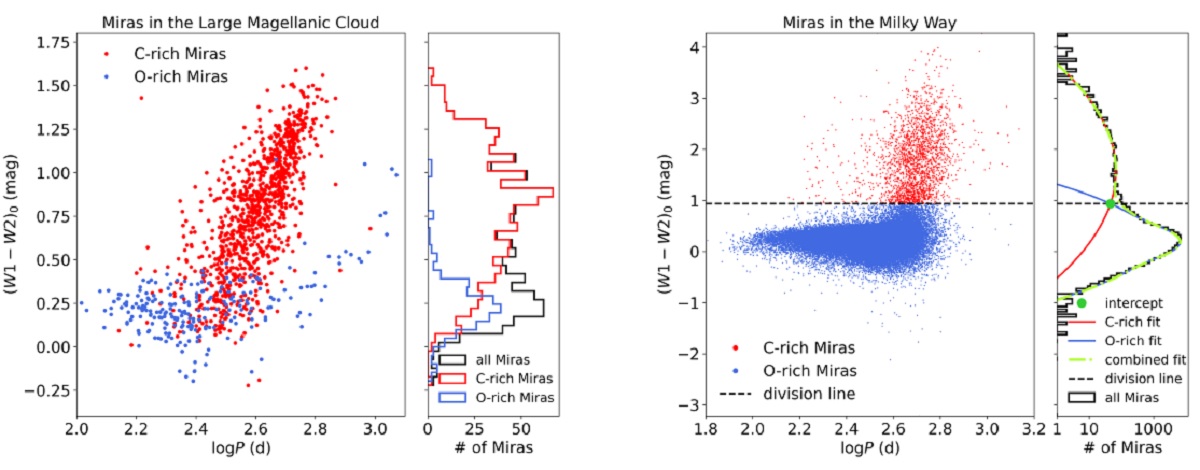
LMC での分類 Soszynski et al 2005, 2009 は Wesenheit 指数を用いて LMC のミラ型星を C- リッチと O-リッチに分けた。しかし、この方法をバルジに適用した結果、 バルジの厚みが大き過ぎるため、この方法は適用できないと分かった。 |
銀河系での分類 Iwanek et al 2021 は MIR カラーと変光周期を組み合わせると分離が可能になることを 示した。図2には (W1-W2)o - log P 図を示す。(W1-W2)o で分類が可能で あることが判る。MW では境界を (W1-W2)o=0 とした。 (W1-W2 カラーだけっていうのは粗すぎ? 特に O-リッチマスロス星と炭素星の混在処理。LMC と MW での差の原因は興味深い。) |
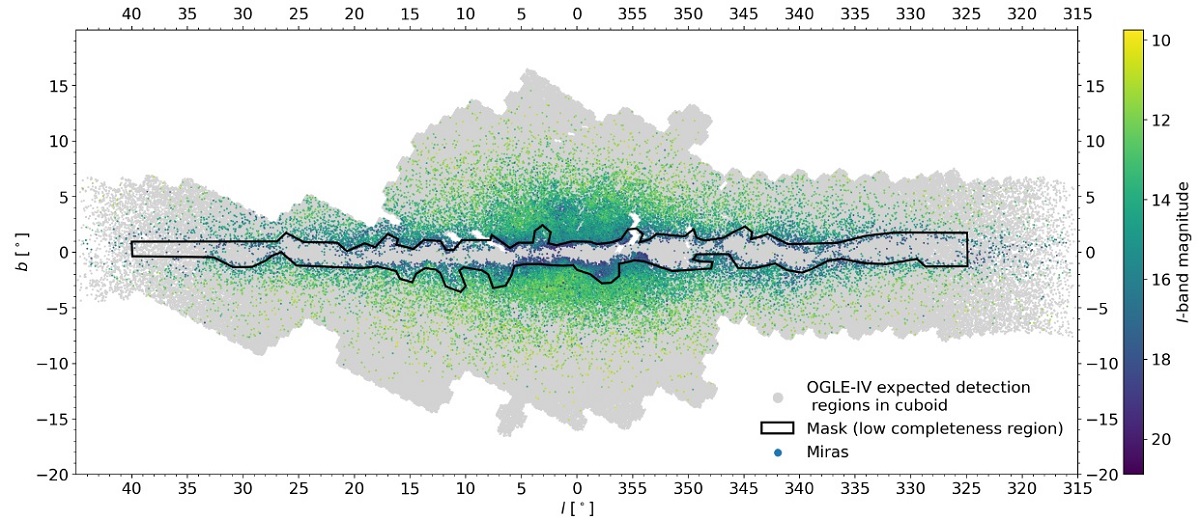
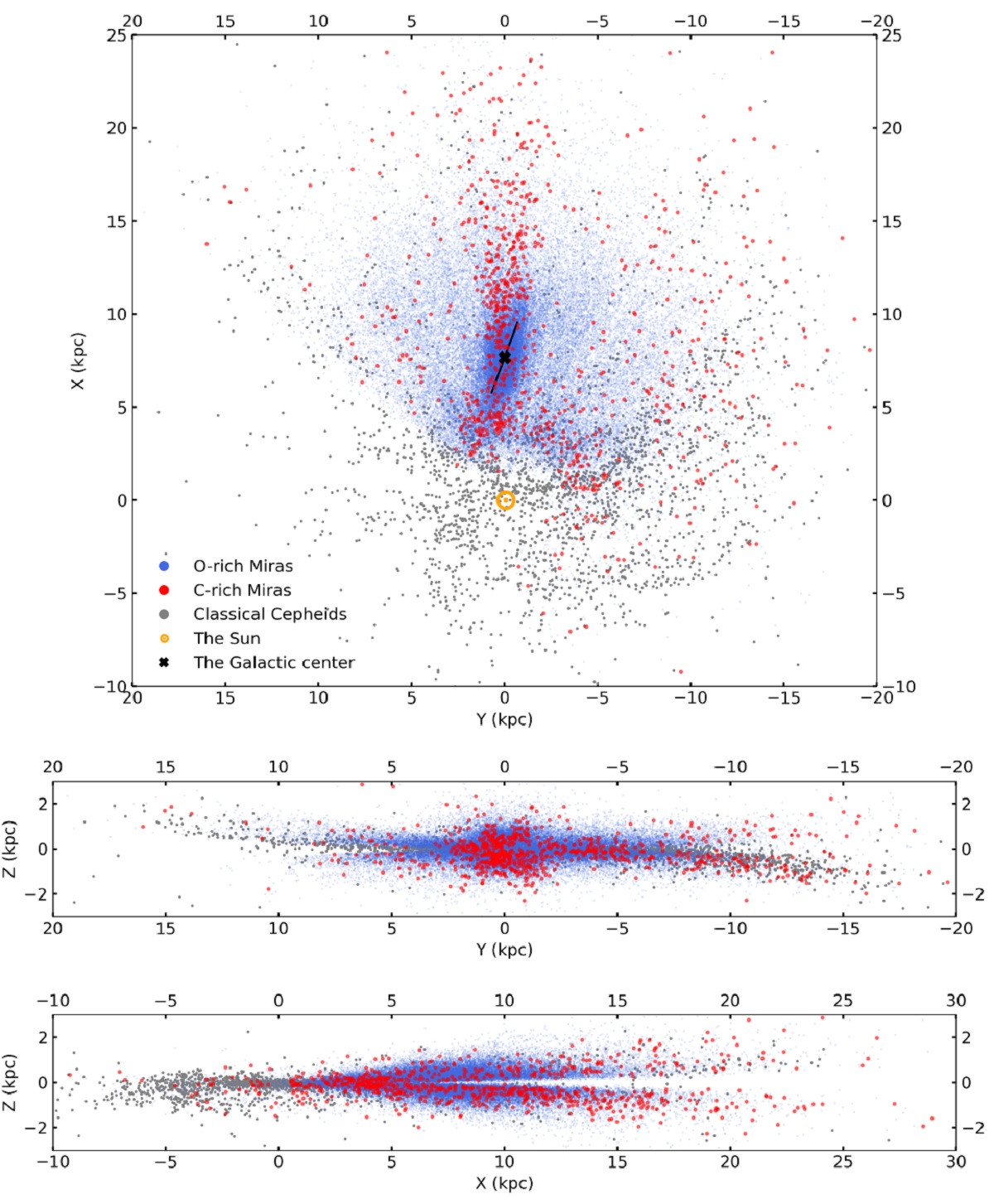
6.1.座標系X= d cos(l)cos(b) = GC 方向 Y = d sin(l)cos(b) = シグナス方向 Z = d sin(b) = 北銀極方向6.2.サンプル選択サンプル範囲X = [4, 12], Y = [-4, 4], Z = [-2, 2] kpc の直方体を調べる。 39,619 ミラがある。 完全性 我々のサンプルには b = [-1°, 1°] が含まれない。更により高緯度 でも分子雲があるところでは星が隠される。その効果は図3を見ると明らかで、 図3の黒枠内の 7180 ミラを解析から除いた。残りは 32,439 星である。表1 ではそれらの星に "mask" = 0 と付けた。 |
炭素星も除く 2244 炭素星も除いた。 6.3.バーモデルSormani22 モデルSormani22 は 39 パラメターのバーモデルを提示した。バーには X-型構造 も含まれる。モデルは多成分分布で Portail17 の N-体モデルを再現するよう にした。Sormani22モデルは ρ = ρbar,1 + ρbar,2 + ρbar,3 + ρdisk ここに、ρbar,1 = バー、ρbar,2 =Xバー、 ρbar,3 = ロングバー、ρdisk である。 |
6.4.フィッティング尤度関数をL(p) = exp(-N)Πi=1Nobsρ (Xi,Yi,Zi; p) としてフィットした。 6.5.バイアスフィットしたモデルは 44 個のパラメターを含む。この様に多数のパラメター があると、バイアスや縮退の影響を被りやすい。 そこで、モックモデルを作ってテストした。 |
6.6.バーフィット |
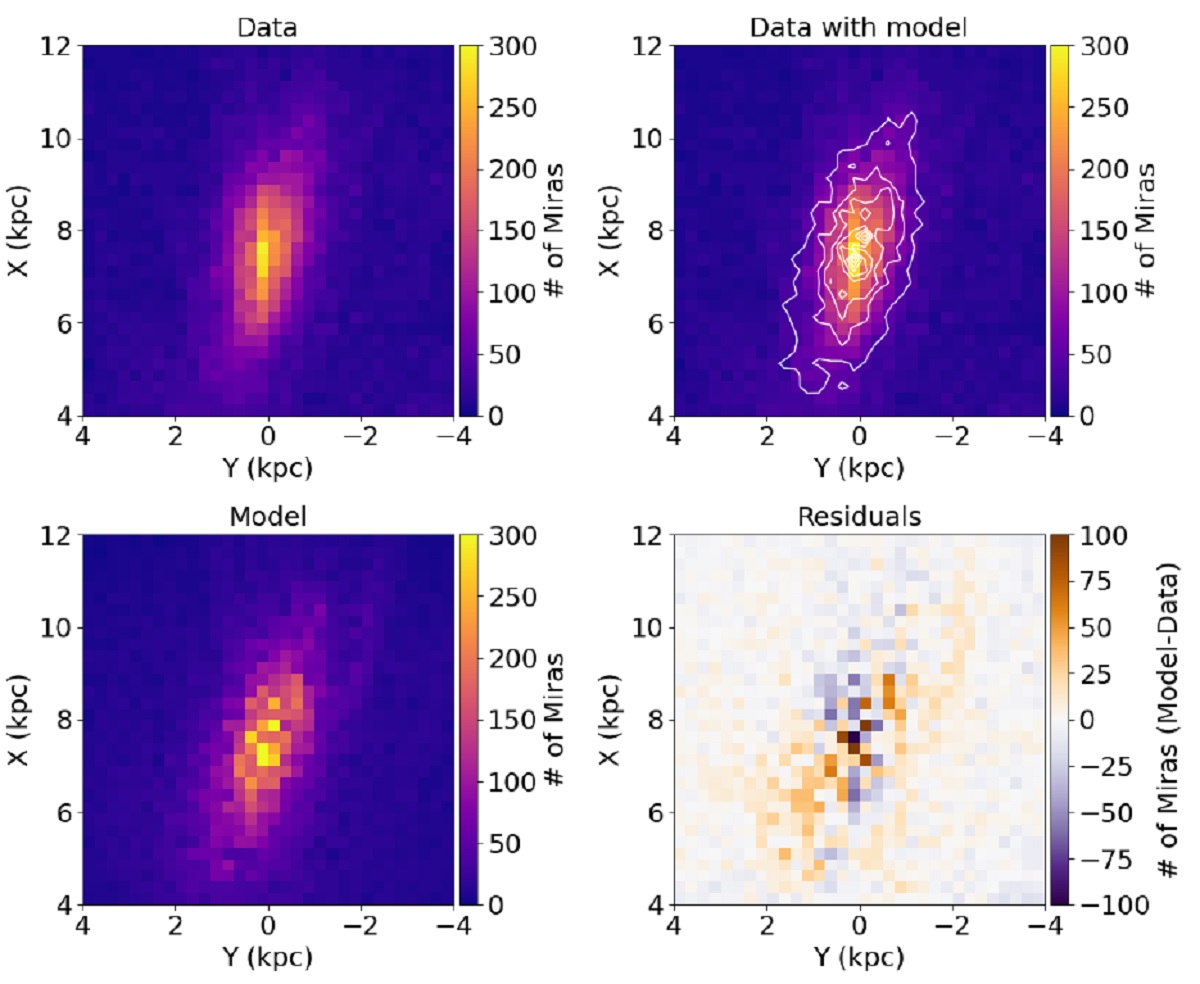
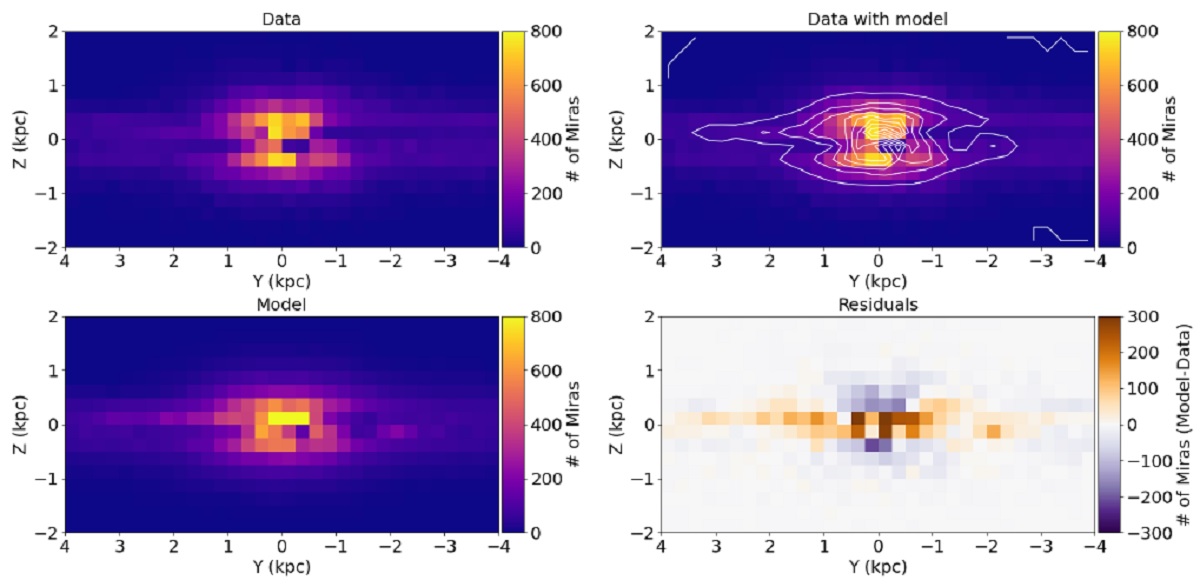
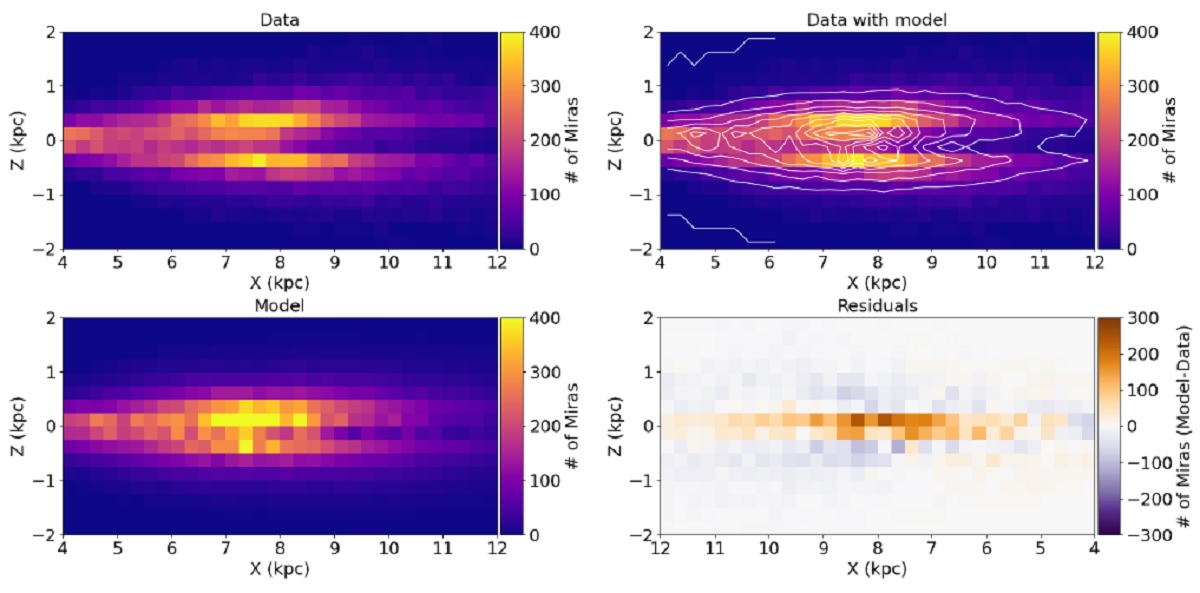
|
Rgc Rgc = 7.66 kpc |
バルジ主軸の角度 θ = 20.2° |