Period-Magnitude Relation of Mira Variables in the LMC as a Tool to Understanding Circumstellar Extinction

　２．データ　

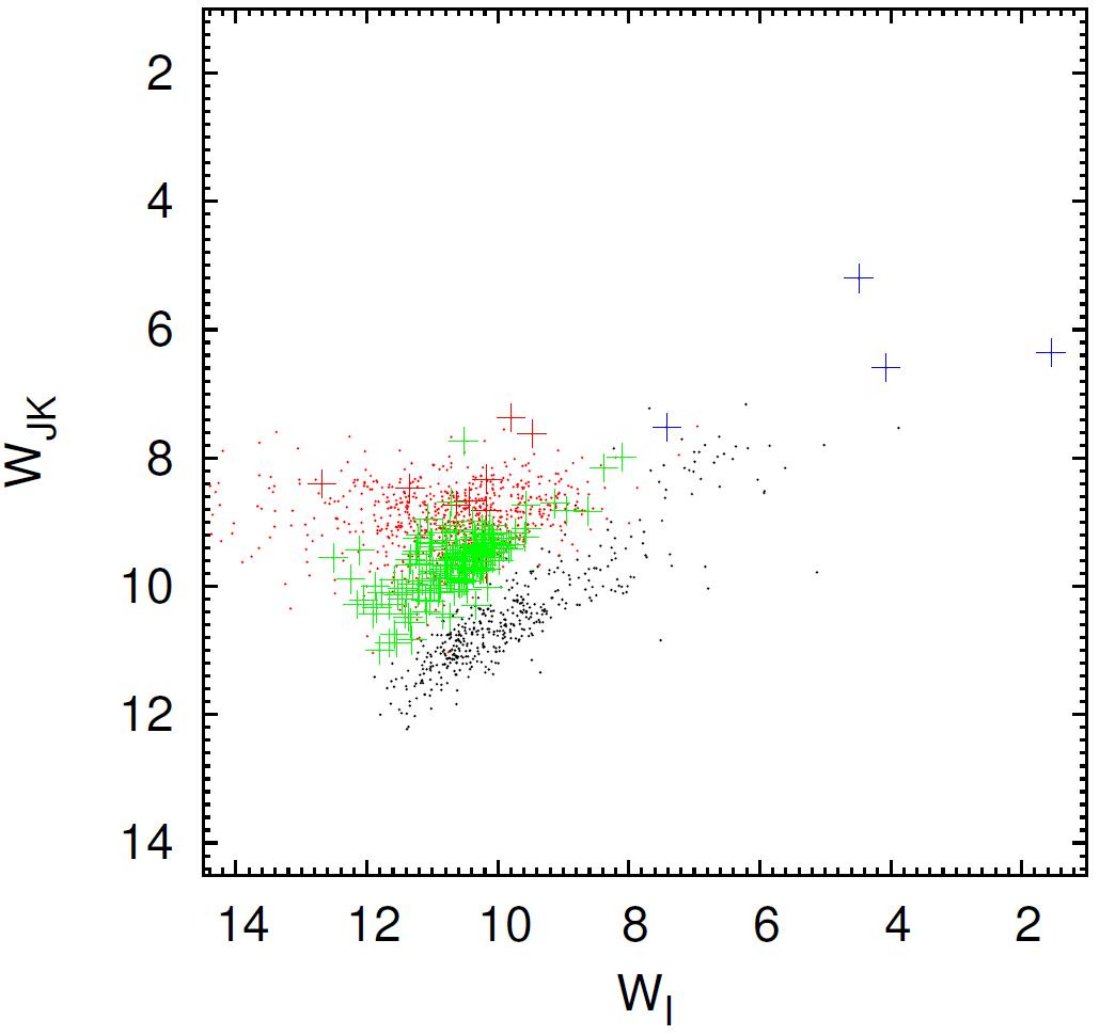
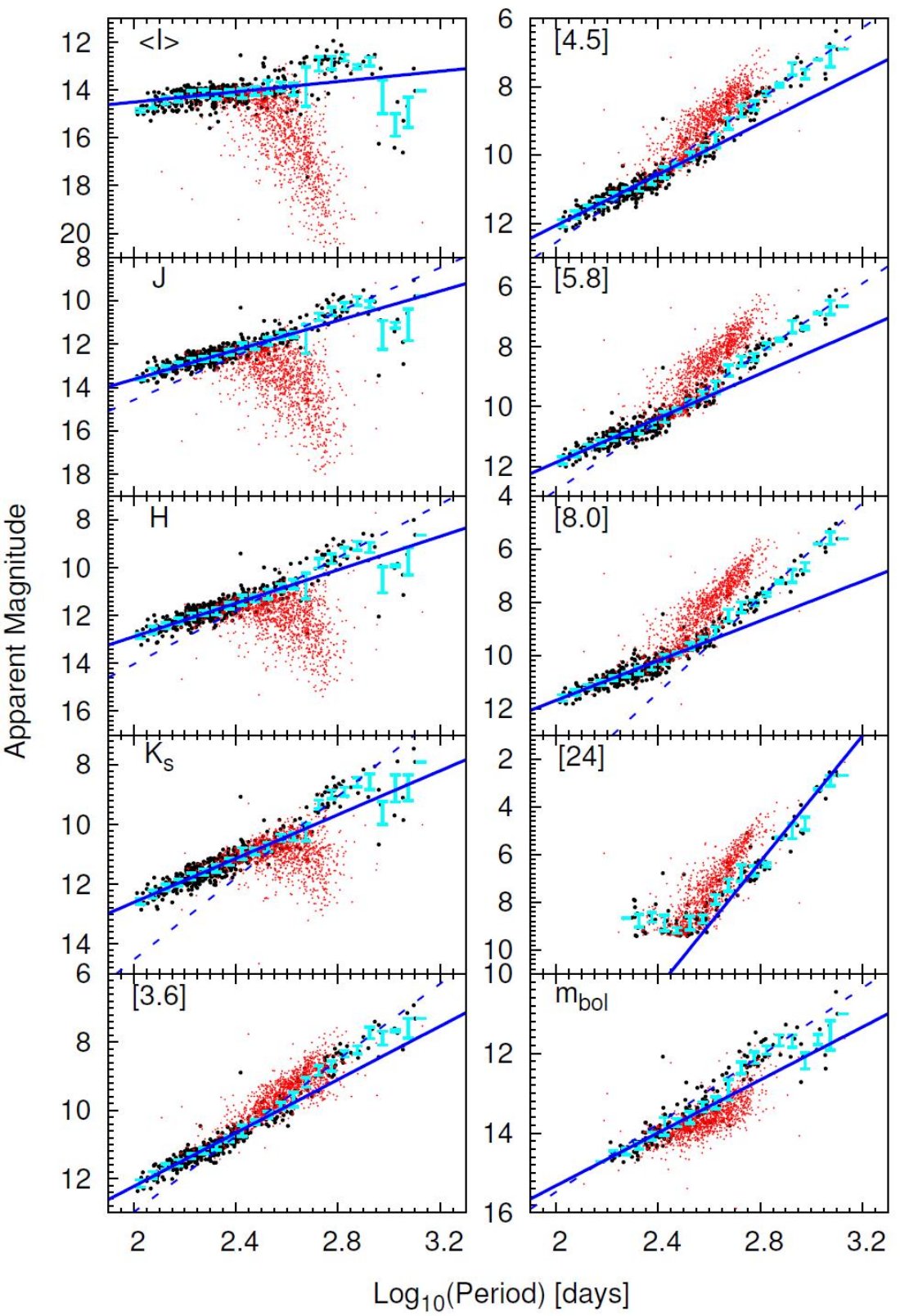
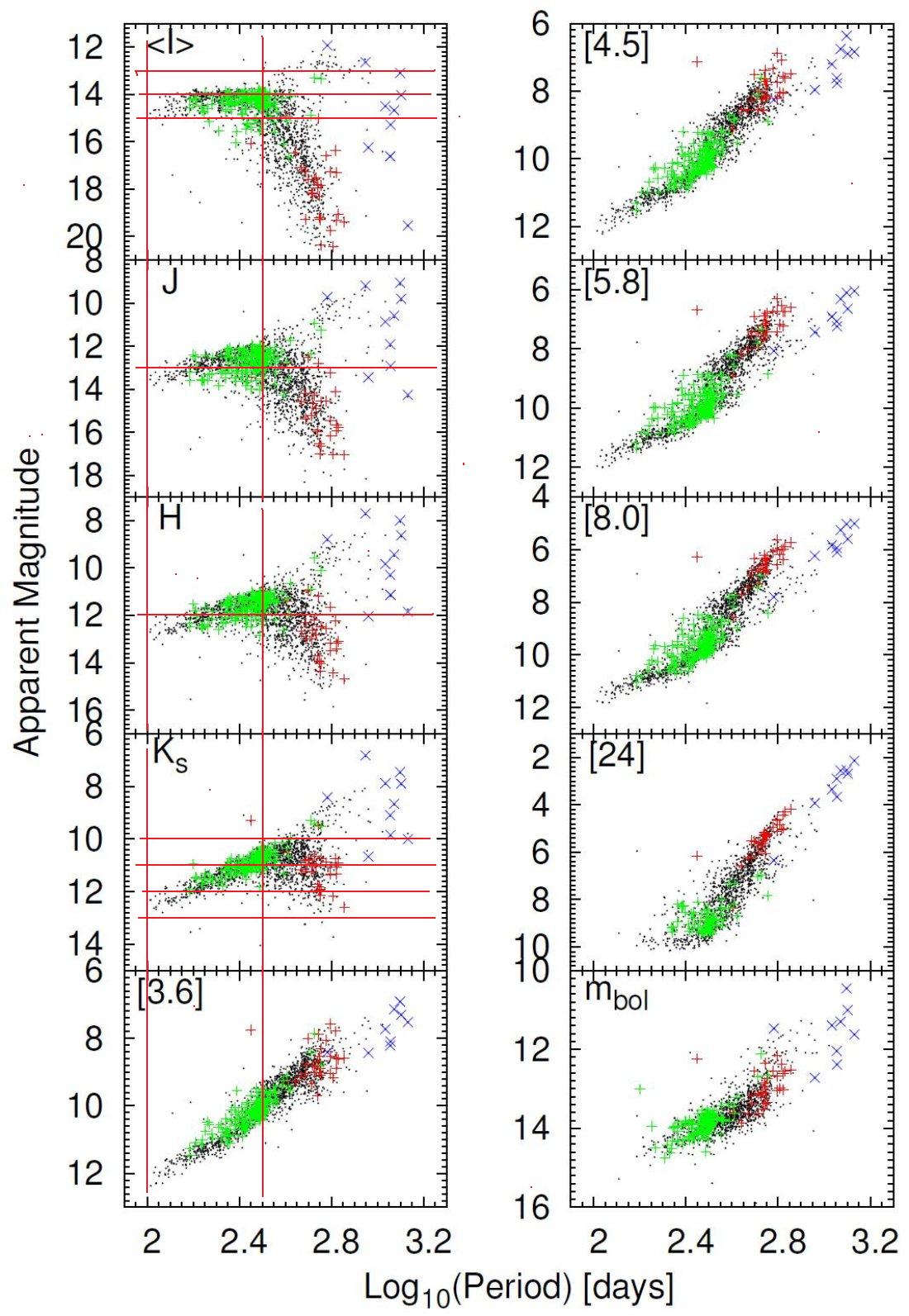
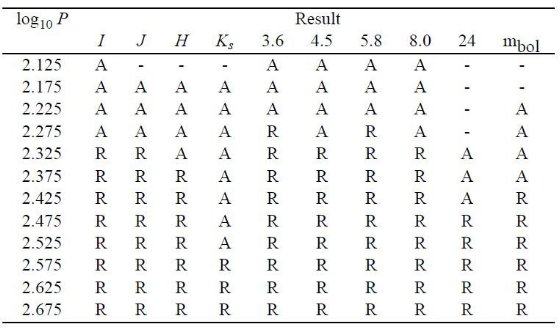
OGLE-III データリリースでは "Mira" をキーにして 1663 個の長周期 変光星を検索できた。Soszynski et al 2009 は ΔI > 0.8 mag をミラ型と定義した。ここでもその用語を踏襲する。彼らのカタログでは カラーから炭素星を分類している。既存カタログとの同定基準は 3 arcsec 以内とした。 　２．１．既存カタログとの同定　 　LMC Photometric Survey (LMCPS) Zaritsky et al 2004 　 　U, B, V, I 等級。64 deg2. V, I は OGLE-III の平均等級 を優先する。 1412/1663 星が同定された・ 　2MASS　 　J, H, Ks 等級。1639/1663 星が同定された。 　IRSF MCPS 　 　J, H, Ks 等級。40 deg2.1557/1663 同定。 　SAGE-LMC Meixner et al 2006　 　[3.6], [4.5], [5.8], [8.0], [24], [70], 49 deg2.最新 カタログリリース DR3 は 2 つのタイプがあり、"Catalog" は信頼度の高い リストで、"Archive/Full" は完全度優先。"Archive/Full" を用いて NIR で 1612/1663, MIR で 1274/1663 の同定を得た。 　可視炭素星　Kontizas et al 2001 　対物プリズムで見つけた 7760 炭素星。163/1663 ミラを同定。 Spitzer 進化した星 Groenewegen et al 2009 　IRS データを一様に調べた結果。66 O-リッチ、68 C-リッチ星の光度とマスロス量 を算出した。 40/1663 同定。

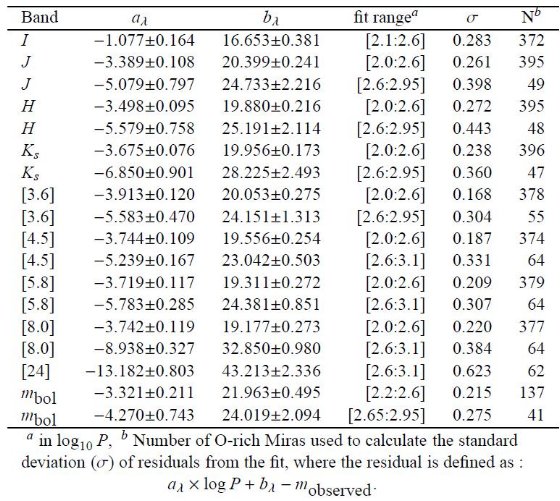
２．２．星間赤化の補正　 　Larsen, Clausen, Storm 2000 の E(B-V) = 0.085 と Av/E(B-V) = 3.2 (Cardelli, Clayton, Mathis 1989) を組み合わせ、(AU, AB, AV, AI, AJ, AH, AKs ) = (0.407, 0.345, 0.272, .159, 0.078, 0.048, 0.032) を全ての星に適用した。Ks より長波長では減光をゼロとした。 　２．３．光度　 　OGLE-III ミラの得られる最短波長から 8 又は 24 μm まで SED を ３次スプラインで結び、積分した。表１にゼロ等フラックスをまとめた。 非常に赤い星では 24 μm より先のフラックスを落としたために得られた 総フラックスが過小評価されている。変光の影響は入れていない。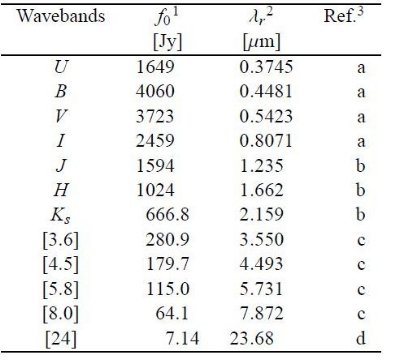 表１．ゼロ等フラックス

　３．結果と議論　

３．１．周期等級関係　 　MIR 周期等級関係 　 Glass et al 2009 　　LMC と NGC 6522 で MIR 周期等級関係は殆ど差がない。 Riebel et al 2010 　　PLR の傾きが星のクラスにより異なる。 本論文 　　OGLE-III + Spitzer DR3 から MIR 周期等級関係を導く。図２。 　短周期での周期等級関係　 短周期ミラはタイトな関係を示す。 O-リッチと C-リッチミラが同じ PMR に従っているかをスチューデント テストで調べた。P < 200 d ミラは組成、波長を問わず同じ母集団 と考えてよい。この PMR 関係を標準関係と名付ける。 　長周期での周期等級関係 　 　P > 320 d になると関係が複雑になる。可視、近赤外で C-リッチ ミラは 標準関係の下にもぐり込むが、Spitzer 波長では標準関係の 上に位置する。これは星周減光の為と理解できるが、固有カラーが赤い ためとも考えられる。一方、O-リッチミラは log P > 3 の超長周期 で標準関係の下に入る。これらの非常に周期の長い O-リッチミラは 銀河系の OH/IR 星に対応すると考えられる。 　O-リッチ変光星の周期等級関係の導き方　 　O-リッチ変光星について関係を決める。 （１）i-番目の Δlog P = 0.05 ビンでの平均等級 ⟨mi⟩ 　　　と標準偏差 σi を求める。 （２）log P = 2.6 で区切り、二本の直線でフィットする。 　　　mλ = aλ log P + bλ 　　　フィットの重みは 1/σi2 とする。 フィットした直線の係数を表３に示す。 残差の標準偏差を 3σ クリッピングを 10 回繰り返してきめた。これも表３に 載せた。 　C-リッチ変光星の周期等級関係　 　炭素星ミラの周期等級関係はフィットしない。なぜなら P < 400 d を 除くと、炭素星ミラは可視、近赤外での関係式に従わないからである。 さらに Spitzer 波長では分散が大き過ぎる。おそらくこれは星周減光の巾が 大きいことと変光の振幅が大きいためだろう。

表２．O-リッチと C-リッチミラが同じ PMR に従っているか のスチューデントテスト。A = Accept, R = Reject。 表３．二本の周期等級関係の係数。 I 等級は一本だけ。

３．３．星周減光　 　標準関係より下の星 　 　折れ曲がり手前の可視ミラでは O-リッチと C-リッチのミラ は同じ PMR に従っている。赤外ミラになると分かれる。 Wood 2003 は LMC の MSX 天体(Egan et al 2001) から赤外ミラが標準周期 等級関係に従わないことを見出した。それらは標準関係より 下に来ている。 　仮定ね　 　我々はここで以下の仮定を置く。 （１）このずれは星周減光による。 （２）星周減光がなければ赤外ミラの PMR は可視ミラの PMR に従う。 面白いのは図２，３から見えるように、ズレと周期の間に相関がない。 また、ずれは振幅にも関係しない。この解釈は Ita in preparation で述べる。 　 ズレがカラーと強い関連　 　図４はズレがカラーと強い関連を持つ事を示す。この結果は近赤外カラーが 星周減光の良い指標である事を示している。二次式でフィットした結果を 表４に示す。 　マスロス　　 　図５を見ると、星周減光曲線は星間減光曲線と異なっているようである。 しかし、以下の計算ではファクターの違いは無視して両者を同じと 看做す事にする。観測された赤外ミラの大部分では標準周期等級関係 より 2 等暗い。極端な場合は 4 等の差を生じている。これは星間減光 曲線を適用すると、前者で Av = 17 等、後者では Av = 34 等に相当する。 この値に van Loon 2007 のマスロス式、 　　　dM/dt = 1.5 ×10-9(Z/Zo)-0.5 (L/Lo)0.75Av0.75(Mo/yr) を適用してみよう。 　　Z = 0.4 Zo. L = 8000 Lo, Av = 15.7 を代入すると、 ( τ を使っている。) dM/dt = 1.6 ×10-5 Mo/yr となる。この値は Groenewegen et al 2009 が SED フィットから導いた値とほぼ同じである。

表４．図４のフィット d = a x2 + b x + c の係数。 図５．ズレの比と周期の関係。黒点＝ O-リッチ、赤点＝C-リッチミラ。 水平線は星間減光の比。 　星周減光曲線　　 　図５にはズレの比を周期の関数として示した。比較のため、星間吸収の 場合での値を水平線として示した。明らかに減光曲線は星間と星周とで 異なっている。 もう一つ興味深いのは炭素星ミラでは、比が周期と共に変わって行くことで、 これはダストの性質が周期と共に変化していることを示す。 この様な結果を星周ダストの性質に拘束を掛けるのに使う事は非常に 興味あることである。