Short Period Mira Variables


Hron
1991 AA 252, 583 - 589



　アブストラクト　

　P ≤ 200 d の短周期ミラは低メタル星と円盤星の混合集団と考えられて いる。測光観測と低質量ミラの大気と脈動モデルに基づいて、両者を分離する 方法を議論する。 　球状星団のメタル組成とフィールドミラの運動学を測光データと結合して、 (Vmax - K)o が円盤星と低メタル星を分離するのに使えることを 示す。現在得られる P = [145, 200] d フィールド星の VJK 測光はこの星 集団内のメタル量の広がりとして -0.5 dex を得た。

　１．イントロダクション　

　短周期ミラと類似の特性を持つ星たち　

　周期 200 d 以下のミラは、低メタル星を含むという直接、間接の証拠を持つ 点で、特異な位置を占めている。 Menzies, Whitelock (1985) は球状星団内のミラが周期 150 - 270 d を持つことを示した。 Feast (1963), Gilmore et al 1989 は周期 150 - 200 d のフィールドミラの運動が RR Lyr とおそらくは [Fe/H] = [-1, -0.5] の球状星団のそれと似ていることを指摘 した。 Hughs, Wood 1991 は LMC にも似たミラ種族を見出した。 このようなわけで、フィールドミラは星の進化および、銀河系の構造に有益な 情報を抱えている。 		　Tc 欠乏　

　周期 P < 150 d のミラの運動は P ≥ 250 d のミラとよく似ている。 その一方で、統計視差はこれらの星が、周期光度関係の延長から下に外れてい ること Robertson, Feast 1981 を示す。したがって、それらの星が本当に ミラの周期・光度・質量関係の下端を代表するのか明らかでない。P < 200 d のミラ大気に Tc がないことは低質量 AGB 星 なので、低光度で熱パルス間隔が長くてドレッジアップされた Tc が崩壊して しまう、という考えに一致する。

　サンプル　

　そこで GCVS から 219 の P < 200 d、Vmax < 11 mag ミラを選んだ。文献から採った運動学データと JHK 測光を用い、メタル量の 違いを分離する方法を探る。

　２、メタル量の測光指標　

　低メタル星は高温　

　分光でメタル量を求めるのは最も正確だが、時間がかかる上、未だにミラ型 星の大気モデルは確立されていない。従って、測光的な指標を調べたい。その ために Bessell et al 1986 のバルジ AGB 星研究方法を採る。彼らは高メタル になると低温になるという事実を用いた。我々は低メタルになると高温になる という事実を用いる。

　ミラの基本関係式　

　Wood 1990 は AGB 星の Mbol, Teff, M, Z の間に次の関係を見出した。

Mbol=15.7[log Teff + 0.12 log(Z/Zo) -d] - 2.65log(M/Mo) - 59.1　(1)

ここに
　　d = 0 　　　　　　　　　　　　　　　x ≥ 0.8
　　　　0.07(0.8-x)2.54 　　　　　　x < 0.8
そして
　　x = Mbol + 7 -1.2/(M/Mo)1.7

Wood 1990 のミラ型星モデルの計算は次の形にまとめられる。

log P = -2.07-3.88(Teff/To)-0.9log(M/Mo)-0.388(Mbol-Mbol,o　(3)

この関係はメタル量の影響をあまり受けない。

　コメント　

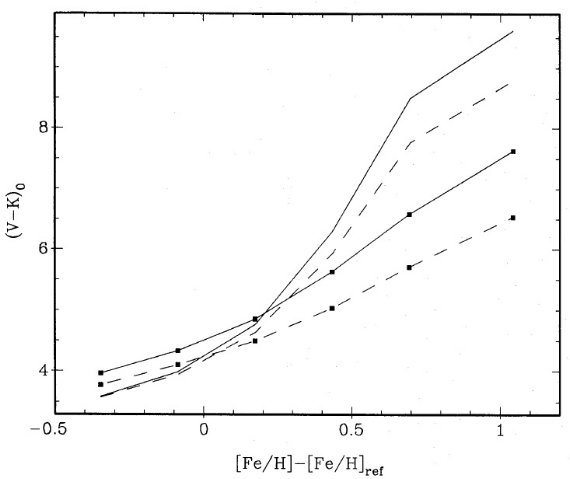
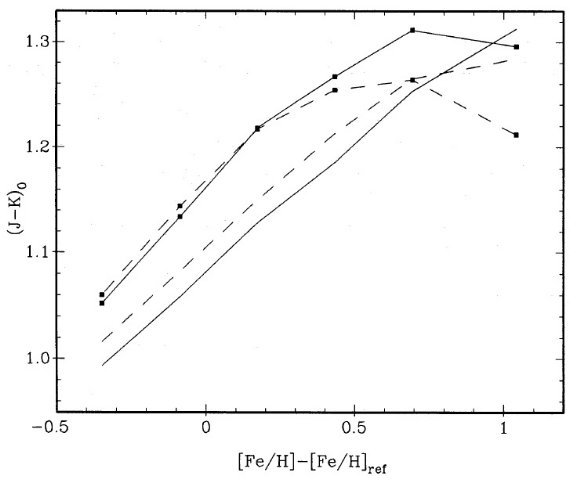
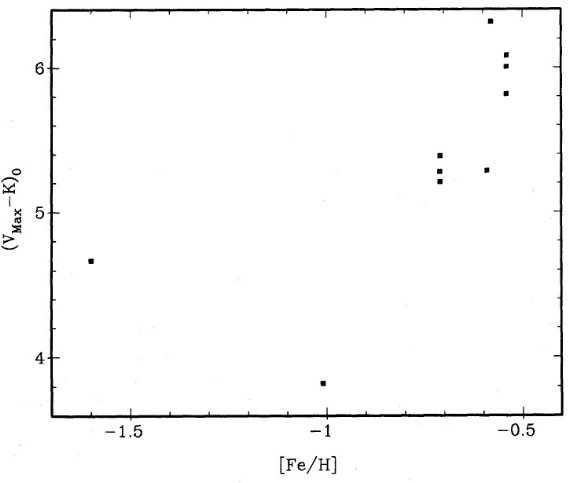
変数は、Mbol, Teff, M, Z, P の５つ。第１式は、HR 図上の AGB, 第２式は 振動関係式。第１式から、AGB 上の一点（Mbol, Teff) に対し、(M, Z) の系列 が対応する。第２式を使うと、AGB 上の一点には (M, Z, P) の系列が対応する ことになる。つまり、AGB の一点に対しては M のある区分と P のある区分が 一対一対応する。それを下文の意味につなげるには、(Mbol,Teff,P)を決めると (M,Z)が決まるから、Mbol を[-3.5, -4] の範囲で動かすと、(M,Z) の小系列が、 つまり M の小区間が生まれると考えればよい。くどいか。 		　上の関係式に、Teff=3600 K, Mbol,o = 4.72, P = 175 d, Mbol = [-3.5, -4] を入れると、M = 0.5 - 0.8 Mo となる。Teff は星団ミラの (J-K)o と Bessell et al 1989a から評価された。
(Teff とカラーの関係は今どうなっ てる？)
Mbol は Menzies, Whitelock (1985) の球団ミラに対する典型値を用いた。このように得られたミラ質量は、星団 RR Lyr の質量が 0.6 Mo 程度であることと整合する。

　Mbol を消去　

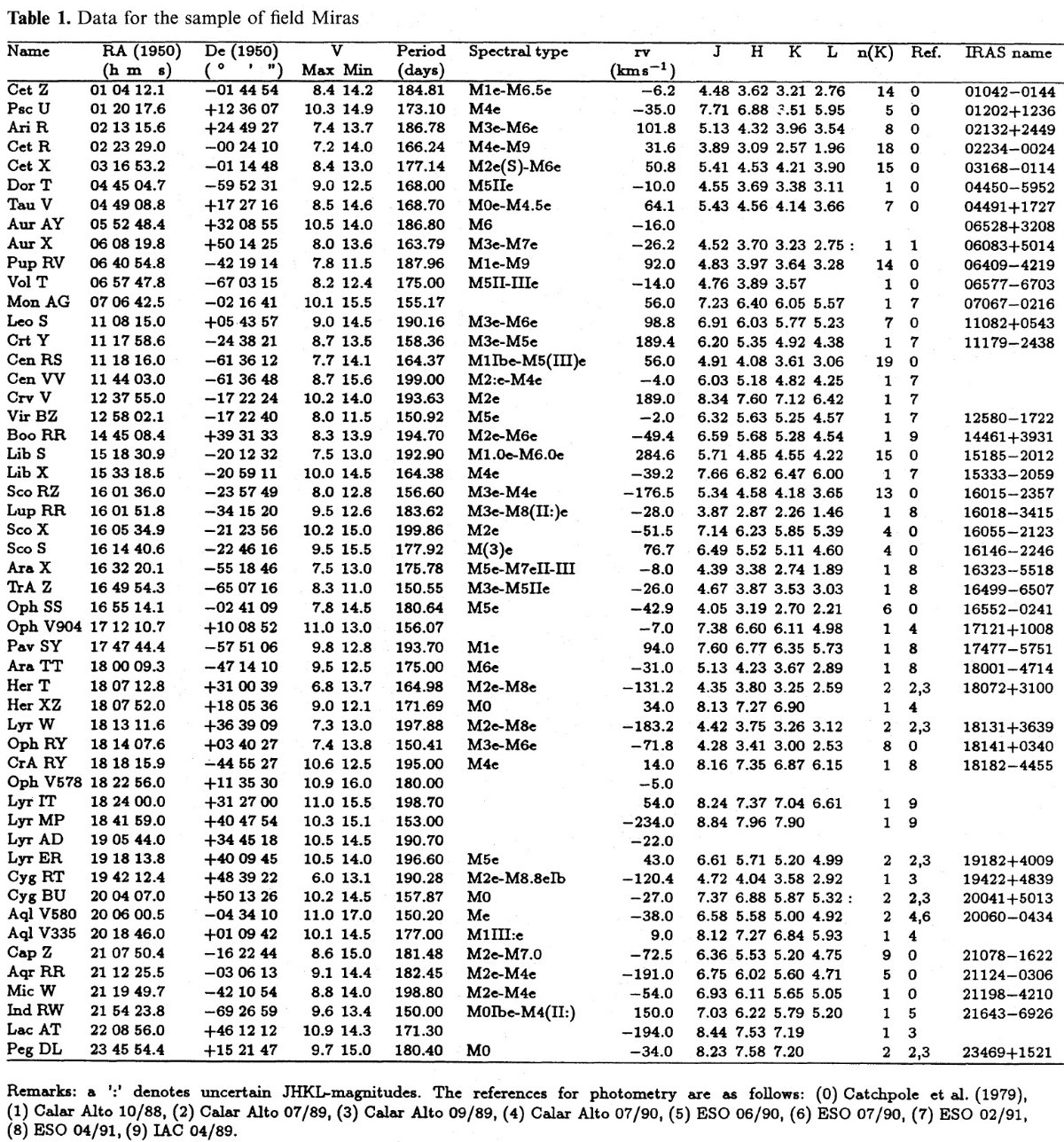
　上の二つの式から Mbol を消去すると、P, M, Z, Teff の間の関係式が出る。 銀河系運動学から、どの周期区間でもミラのある割合は円盤星であることが判 る。( Feast (1976) の図６)　それらのメタル量は太陽と同じくらいと仮定して よい。ミラのメタル量を推定するには、円盤星と低メタル星の間で、Z によっ て Teff がどう変化するかを知れば十分である。
(理解できない。 )

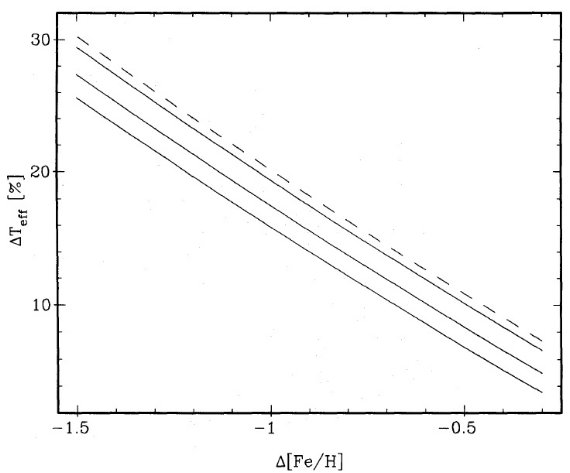
Mbol を消去した結果は、

ΔTeff = -0.10Δlog P - 0.07Δlog(Z/Zo) +
　　　　　　　0.01Δlog(M/Mo) + 0.61Δd　　(4)

Δd は M と Mbol を内包している。P < 300 d のミラは銀河系運動学 （Feast 1989）から 1 Mo が上限であり、RR Lyr 質量から下限は 0.6 Mo で ある。星団ミラ及びフィールドミラの統計視差から Mbol = [-3.5, -4] (Robertson, Feast 1981) である。この光度範囲では d がゼロでないのは、 質量下限でのみである。したがって、低メタル星と円盤星とはほぼ同じ程度の 質量、つまり 0.6 - 1 Mo を持つならば、Δd はゼロである。もし、 円盤星が上限近くの質量 M を持ち、低メタル星質量が下限近かったら、 Δd は最大値をとるがそれで 0.02 である。

　Teff の差　

　図１は [Fe/H] の差に応じた Teff の差を示す。メタル量の範囲として、 球状星団でミラが存在する範囲 Menzies, Whitelock (1985). Armandroff 1989 の [Fe/H] = [-1.5, -0.3] を選んだ。図の上と下の実線は 周期区分の P = 175±25 d の効果を示す。もしも低メタルフィールド 星が球状星団ミラと似ているなら、予想される Teff の差は大体 10 % くらい である。周期の広がりはその周りに大きな散らばりは生じない。
(図１は式 (4) の ΔTeff の式 をグラフにしたものと思う。その際式(4) 右辺の Z 項以外は どう扱われているのか不明。 Z 項は -0.07Δlog(Z/Zo) なので、[Fe/H] = -0.5 から -1.5 へ 1.0 変わると、 Δlog Teff が 0.07 変わる、これは 10^0.07 -1 = 0.17 ≒ 20 % に相当する。つまり、図１の勾配は Z 項の傾きとまあ看做せる。)

破線はもし低メタル星に 0.6 Mo を円盤星に 1.0 Mo を適用した時の温度差を 示す。
(これは (3) 式に 0.01Δlog(M/Mo) = 0.01 log(1/0.6) = 0.002 の効果か？これだと 0.46% にしかならないが？)

こうして最大効果は 2 % の温度上昇である。

図１．AGB 星のメタル量変化と有効温度変化の関係。上と下の実線は周期の巾 175±25 d の効果を表す。破線は M と Mbol の効果を表す。


図２a．M-巨星の (V-K)o のメタル量差による変化。実線＝ 104 Lo, 破線 = 2 103 Lo.黒丸付きは太陽組成。 黒丸無しは [Fe/H]=-1 組成。 　

　Teff からカラーへ　

　この結果を観測に応用するには、これらの量を観測量に変換しなければ ならない。Bessell et al 1989a の 通常 M-巨星のカラーを用いて、(J-K)o と (V-K)o が温度依存が最も大きいことが判る。Bessell et al 1989b の ミラ大気の実験的なモデルによると、 T > 3200 K のミラでは (J-K)o と (V-K)o は依然としてよい温度指標である。注意しておくが、彼らは メタル ラインオパシティと TiO バンドの幾つかを入れていないために、(V-K)o の再現には失敗した。しかし、彼らの differential colours は (V-K)o と Teff の観測的関係と良く合う。
("differential colours" って 何だ？)

　(Teff/Tref) へのメタル量の影響　

　Tref = 3600 K と定義する。式 (4) で P, M, d の違いを無視すると、

　　　(Teff/Tref) = 10-0.07([Fe/H]-[Fe/H]ref)
　　　　　　　　　= 1 - 0.16([Fe/H]-[Fe/H]ref)　　　(5)


(これはつまり、ある ref 星をとり、 ref 星と同じ周期、同じ質量の星を較べた時、星を規定する残りのパラメタ―は メタル量だけであり、メタル量の影響は上式で与えられる、ということである。 )

図２b．M-巨星の (J-K)o のメタル量差による変化。実線＝ 104 Lo, 破線 = 2 103 Lo.黒丸付きは太陽組成。 黒丸無しは [Fe/H]=-1 組成。 　

　図２＝カラー　

　(5) 式をカラーに直して、 (V-K)o と (J-K)o に対する影響を図２に示す。 カラーはまたメタル量に鋭敏なので、太陽組成と [Fe/H]=-1 のモデルに対して 図２を示す。Tref の値は球状星団ミラの典型値であり [Fe/H]=-0.5 付近 である。円盤星は図２を見ると、(J-K)o で 0.15 mag, (V-K)o で 2.5 mag より赤いはずである。

　(V-K)o が使える？　

　(J-K)o の差からメタル量を推定するのは困難である。一方、 (Vmax-K)o の方の信頼度は 1.5 mag くらいなので、メタル量の差を検出 出来るだろう。
(横軸が [Fe/H]-[Fe/H]ref の図上に [Fe/H] = 0 と -1 のラインが引いてあるのは全く理解できない)

　３．球状星団中のミラ　

　サンプル　

　球状星団ミラのサンプルを Menzies, Whitelock 1985 から採り、Vmax を Hogg 1973 から、メタル量と赤化を Armandroff 1989 から得た。赤化 に関し、M-型星では R = 3.6 の方が R=3.2 より良い。

　カラーとメタル量関係　

　図３には、球状星団中ミラ P = [150, 220] d の (Vmax-K)o - [Fe/H] 関係 を示す。(Vmax-K)o がメタル量低下と共に下がって行くのが明らかである。 再び、[Fe/H]=-0.5 をレファレンス値に採ると、[Fe/H] = -1 の星は (Vmax-K)o で約 1 mag 青いはずであることが図２から分かる。
(全然分からない。) しかし、図３からは観測差が 1.5 mag と出る。これは上の評価より大きいが 観測誤差等を考えると重大ではない。

図３．球状星団中ミラ P = [150, 220] d の (Vmax-K)o - [Fe/H] 関係




表１．フィールドミラサンプルの諸データ

　４．フィールド星への応用　

　４．１．フィールドミラのデータ　

　４．２．運動学的メタル量および測光的メタル量　


図４．|sin l|　< 0.7 フィールドミラの VLSR と (Vmax-K)o の関係。

　減光　

　van Herk 1965 の銀河系減光モデルを使った。ただし、 E'(B-V) = 0.23 mag/kpc　を Lynga 1982 に合わせて採用した。銀緯のサンプル平均は 25 ° で大きいので、赤化の影響は小さい。

　VLSR　

　視線速度は太陽運動を (uo,vo, wo) = (-9, 12, 7) km/s として、VLSR に直した。

　銀経で二つに分ける　

　次に二つのグループに分けた。

（１）|sin l|　< 0.7
　　　　VLSR は銀河系の動径方向の速度分散を反映。

（２）|sin l|　≥ 0.7
　　　　VLSR は集団の平均回転速度とその周りの速度散らばりを 反映。

　グループ１　

　図４にはグループ１の VLSR を(Vmax-K)o の関数として示す。 赤いミラの速度分散が青いミラよりも大きいことが判る。これは低メタル 星が円盤星より高温で青いとすれば納得できる。
( 同じ温度でも青いということでは なく実際に高温？)
青いミラの数が少ないので、統計的にはっきりしたことは言えないが、 (Vmax-K)o =4.5 付近で遷移が起きている。

図５．|sin l|　≥ 0.7 フィールドミラの Vlag と (Vmax-K)o の関係。

　グループ２　

　図５はサンプル２に対する同様の図である。 図５では Vlag = r*VLSR/(sin l)/(cos b) を用いた。これは 各星の VLSR を円回転運動の視線方向成分と看做すことを意味 する。もしサンプル内に低メタル星が含まれていれば、それらは青い (Vmax-K)o、負に大きな Vlag, 大きな速度分散を示すだろう。 これに対し、円盤星は赤いカラー、ゼロに近い Vlag、小さい 速度分散を示すだろう。図５には正にそのような傾向が現れている。 遷移カラーは (Vmax-K) = 4 付近にくっきりと現れている。

　速度分散の違い　

　もし (Vmax-K)o < 4 の星を低メタル星と看做すと、二つのグループ間の 平均カラーの差は 2 mag で、図２を見るとメタル量 0.5 dex の差に相当する。 図５からグループ２の Vlag = -100 km/s 程度である。この 平均 Vlag で VLSR を補正して速度散布度として σlos = 100 km/s を得た。低メタルミラの視線速度分散 と Vlag の値は高メタル RR Lyr と高メタル球状星団に近い。 　円盤星では σlos = 40 km/s である。この値は P > 300 d ミラ の散布度 (Feast 1981) より小さく、古い円盤種族星の値 (Mihalas, Binney 1981) に近い。

　(J-K)o では？　

　図４と図５に対する (J-K)o のプロットは観測エラーに支配される。 グループ１と２に対して (J-K)o の平均値を計算すると 1.14±0.01, 1.23±0.05 mag を得る。このカラー差はメタル量差に合致する。

　５．検討　

　(Vmax-K)o の有用性　

　(Vmax-K)o がメタル量推定に使えそうである。しかし、二つの重要な 効果が残されている。(i) は円盤星と低メタル AGB 星との間の光度差、 (ii) はマスロスの差である。IRAS によると短周期ミラの中でほんの少数しか [12-25] が 10-7 Mo/yr に対応する価に達していない。 (Hron 1990, van der Veen, Rugers 1989) それらは全て円盤的な運動学を 有している。星周赤化が円盤星と低メタル星の間に系統的なカラーの差 を生む可能性はあるが、マスロス量は小さすぎて (Vmax-K) に 2 mag の 差を生じるには足りない。また、そのような大きさの差は (J-K)o に 0.3 mag の差を生じるであろう。そのような差は見られない。
( 円盤星と低メタル星の固有ＳＥＤ は V-K では 2mag の差があって、J-K では 0.1-0.2 mag 差のような ものなのか？)
　次のステップ　

　次のステップはフィールドミラの全サンプルに同様の解析を行うことである。 ただし、(Vmax-K) 解析が可能なのは Teff > 3200 K であることを忘れては いけない。