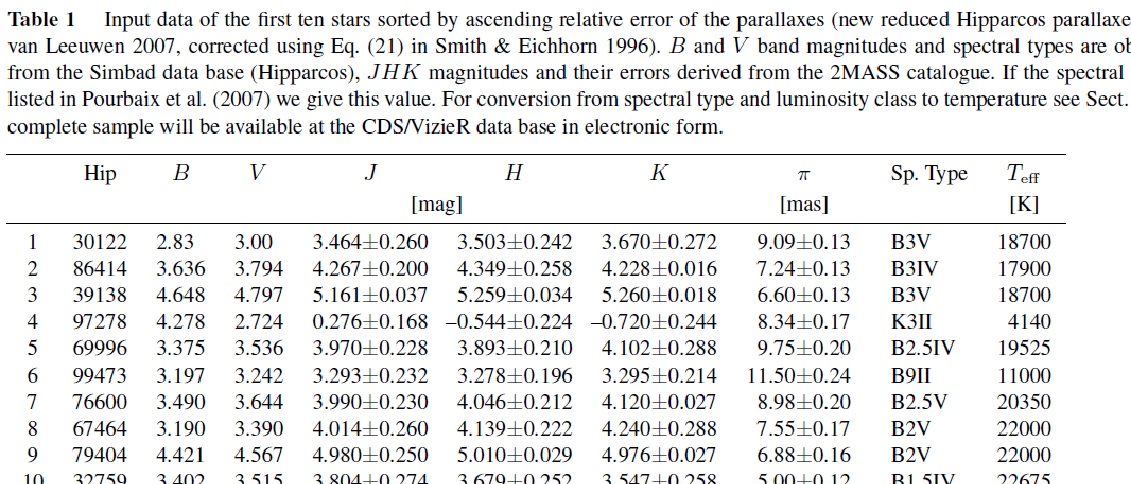
| O-, 早期 B-型と 3 kpc 内の全ての赤色超巨星を調べた。サンプルは 2MASS 観測とヒッパルコス視差があるものに限った。スペクトル型、光度クラス、 多色測光値から減光補正を行い、絶対等級を求めた。進化モデルと光度、カラー を比較して、質量、年齢を定めた。 | 3 kpc 以内のサンプル星全ての光度を使い、光度クラス I, III, V の平均 等級をスペクトル型に対して計算した。以前のデータは連星を分離していなか ったのと、距離を大きく見積もっていたために光度を大きく評価していたこと がわかった。質量と年齢の分布から太陽から 600 pc 以内の超新星率を 今後 10 Myr で 20 回/Myr と評価した。 |

|
サンプル選択 集めたのは超新星になるであろう星=光度クラス V, IV では B4 より早期、 光度クラス III では B9 より早期、光度クラス I, II は全てのスペクトル型 で 3 kpc 以内の星である。この距離は B3V より早期の星が Av = 2.5 mag で も完全なサンプルが得られるように選んだ。Simbad から選んだこのリストに は 16,304 星が含まれる。その内 3042 星が van Leeuwen 2007 の改訂ヒッパ ルコス視差を有す。さらに 2713 星には 2MASS JHKs 等級がある。マゼラン雲 の星が誤って紛れ込む例があったので、 LMC から 7°, SMC から 3.5° 以内は外した。こうして 2668 星が残った。 |
連星 連星カタログ、Simbad から連星情報を集めた。302 星には伴星のデータが 足りないので、例えば主星光度を正しく決められない。これらの星はリストか ら外した。これで 247 連星+2076 単独星= 2323 星となった。 |
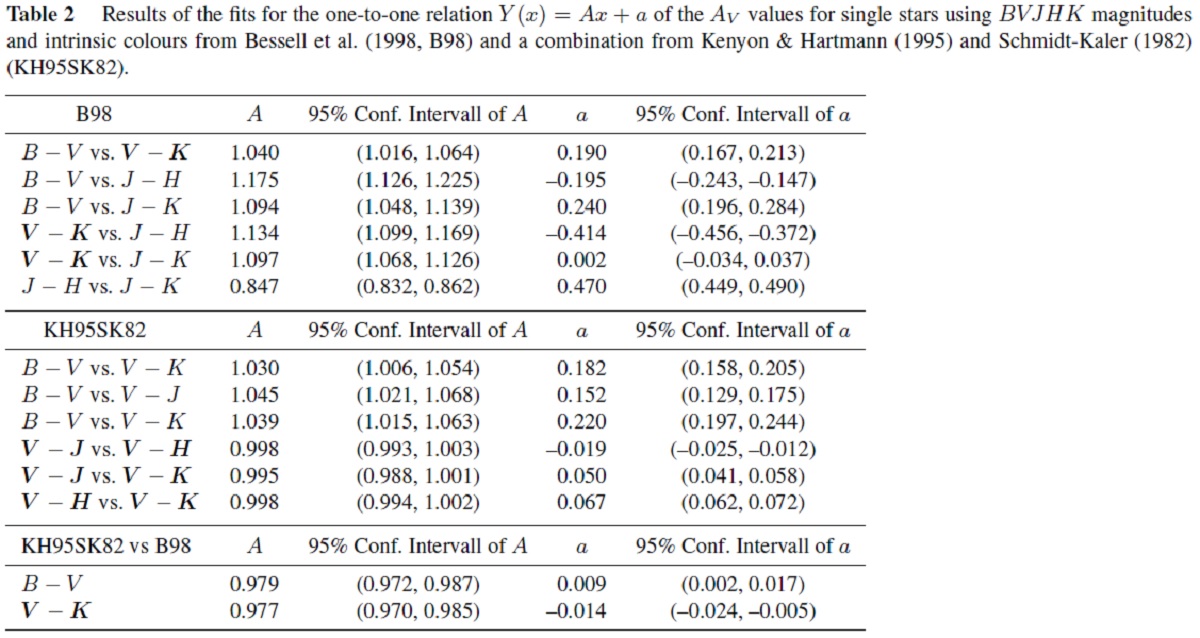
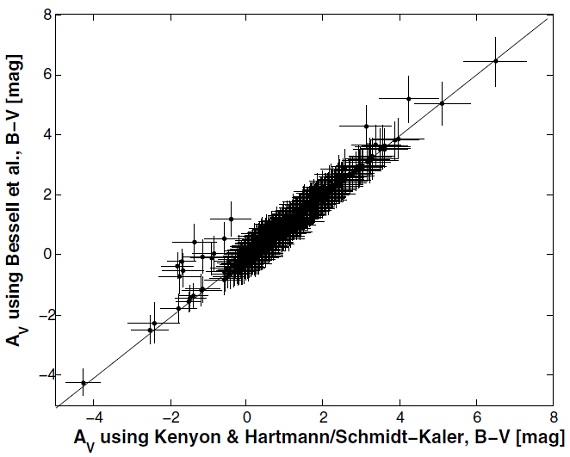 図1.(B-V) からの2通りの Av の比較。 固有カラーと輻射補正 Hohle et al 2009 に従い、BC には Bessell et al. (1998), Kenyon, Hartmann 1995, Schmidt-Kaler 1982 を用いた。 それらを合わせると、全種類の星に対して固有カラーと輻射補正を得られる。 Av 2323 星の BVJHK カラーから Av を計算した。スペクトル型から固有カラー (X-Y)o を求め、観測カラー(X-Y)と比べて色超過 E(X-Y)= (X-Y)-(X-Y)o を 計算し、減光曲線 Av = R(X-Y)*E(X-Y) を適用すると、星 i のカラー(X-Y) に対し、減光 Av(X-Y,i) が得られる。それらの全てからカラー間で比較した 結果 Av(X-Y,i) = A*Av(W,Z) + a が表2である。 (不十分な記述を補った。) |
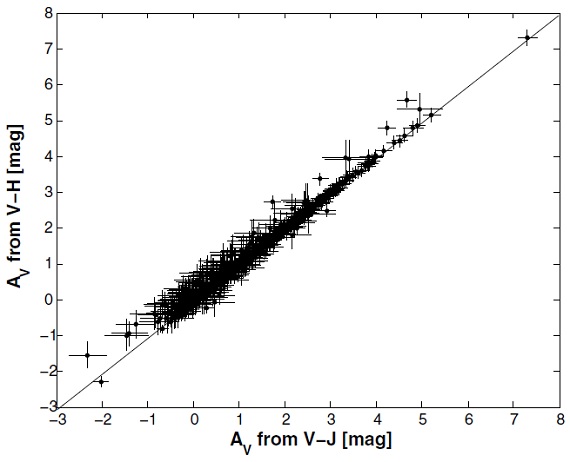 図2. (V-J) からと(V-H) からの Av との比較。 その例は表2に載っている。表2の太字カラー Kenyon,Hartmannn95/ Schmidt-Kaler98 の V-K, V-J, V-H と Bessell98 の V-K を最終的な減光計算 に選んだ。この 4 カラーからの Av 平均値を各星に対して与えた。 109 星では Av < 0 になったが 1 σ 内なので Av = 0 とした。 247 連星系の Av 分解された 247 連星系に対しては各成分毎にスペクトル型と可視等級が 分かっているので、未分解の 2MASS 等級を各成分に分割した。そして単独星 と同じ手続きで Av を定めた。 |
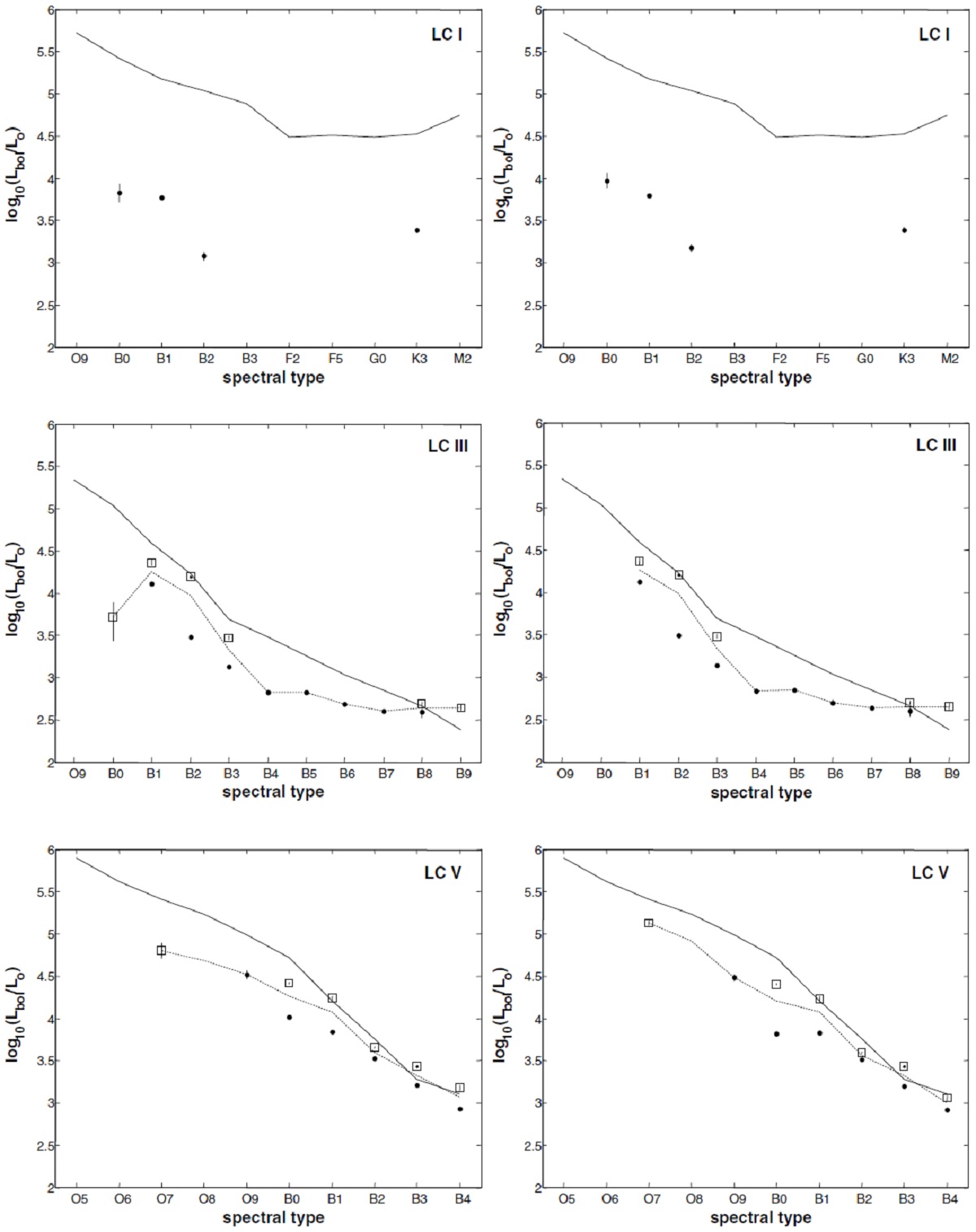
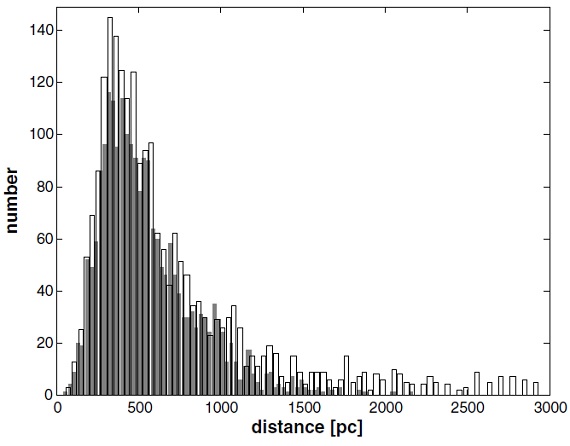 図3.白棒:van Leeuwen 2007 ヒッパルコス距離ヒストグラム。 灰色棒: Smith,Eichhorn 補正距離。 距離補正 D = 1/p で距離を求めるとエラー効果で大きめに出る。この効果を考慮した エラー依存の距離導出 Smith,Eichhorn 1996 を採用した。それでも D > 1 kpc ではエラーが観測 p 値と同程度となり信頼性が薄くなる。残念ながら OG-型星の多くがその範囲になる。 1563/2323 星は D < 600 pc で良いヒッパルコス距離が与えられる。 それらの星には Smith,Eichhorn 補正の影響は小さい。 HR-図 光度は通常の式で計算される。 log L = 0.4(5logD - 5 + 4.74 - BCv + Av) スペクトル型から決めた Teff と合わせて作った HR-図を図5に示す。 図6では得られた光度の中間値を Schmidt-Kaler 1982 の(標準)光度 と比較した。Schmidt-Kaler82 は系統的に明る過ぎる。 Wigner07 の光度 Wegner07 は我々とほぼ同じ、だが A2 より晩期の星について、L を計算した。 そこでは (B-V) から Av が与えられ、他のカラーからの Av は考慮されていな い。晩期型超巨星に対する彼の光度は Schmidt-LKaler82 と比べ 1.5 mag 暗い。 |
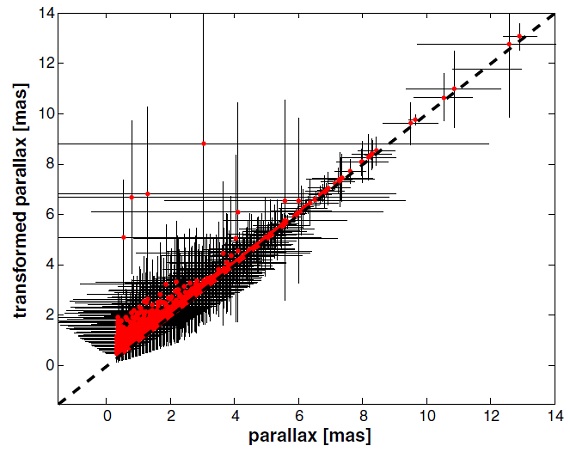 図4.赤丸=van Leeuwen 2007 距離とそれに Smith,Eichhorn 補正を施した 距離との比較。点線=one to one 関係。 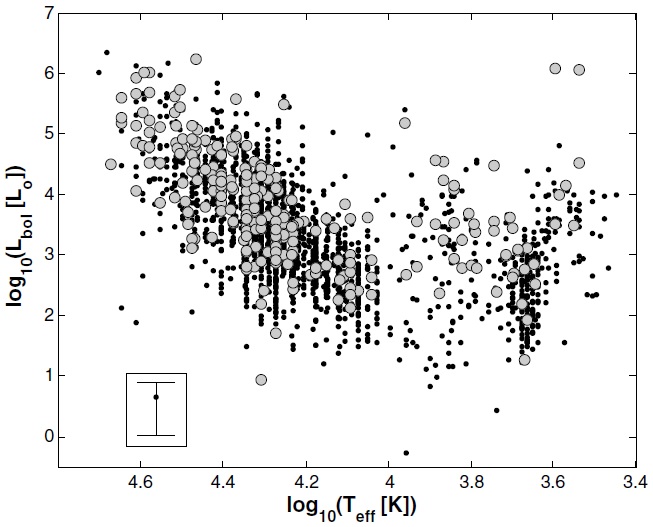 図5.黒点=2323 星と灰色丸=247 分解連星の HR 図。主系列は視差エラー のため太くなっている。光度計算には Smith,Eichhorn 補正距離を使用した。 |
|
半径 光度と有効温度とから半径が求まる。それらを Pasinetti-Francassini et al 2001 の値と図8で比べた。一致は良い。 |
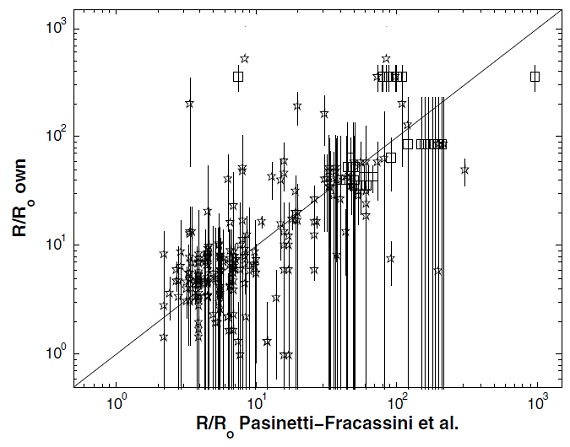 図8.半径の比較。 |
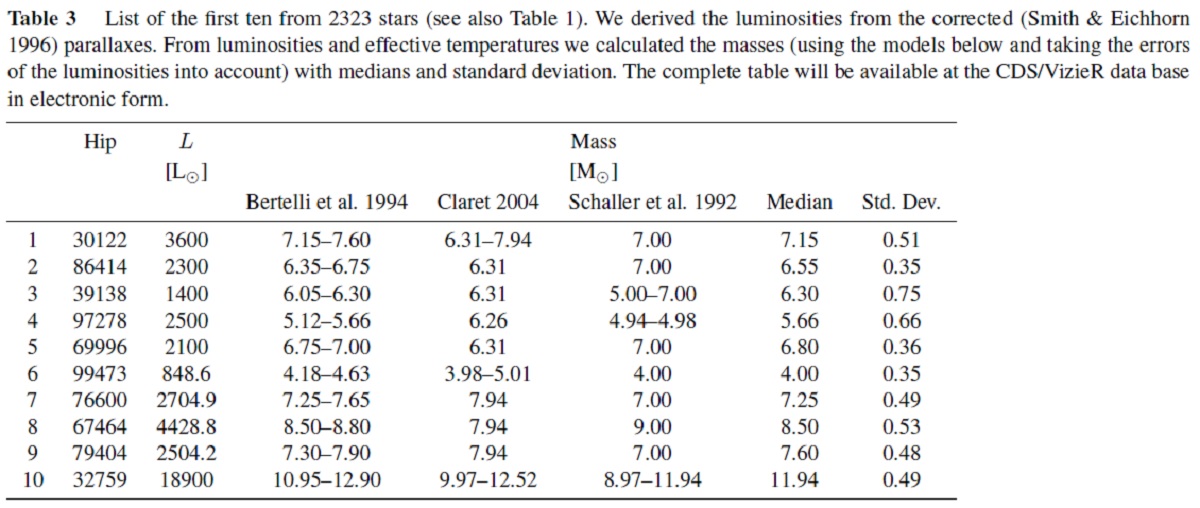
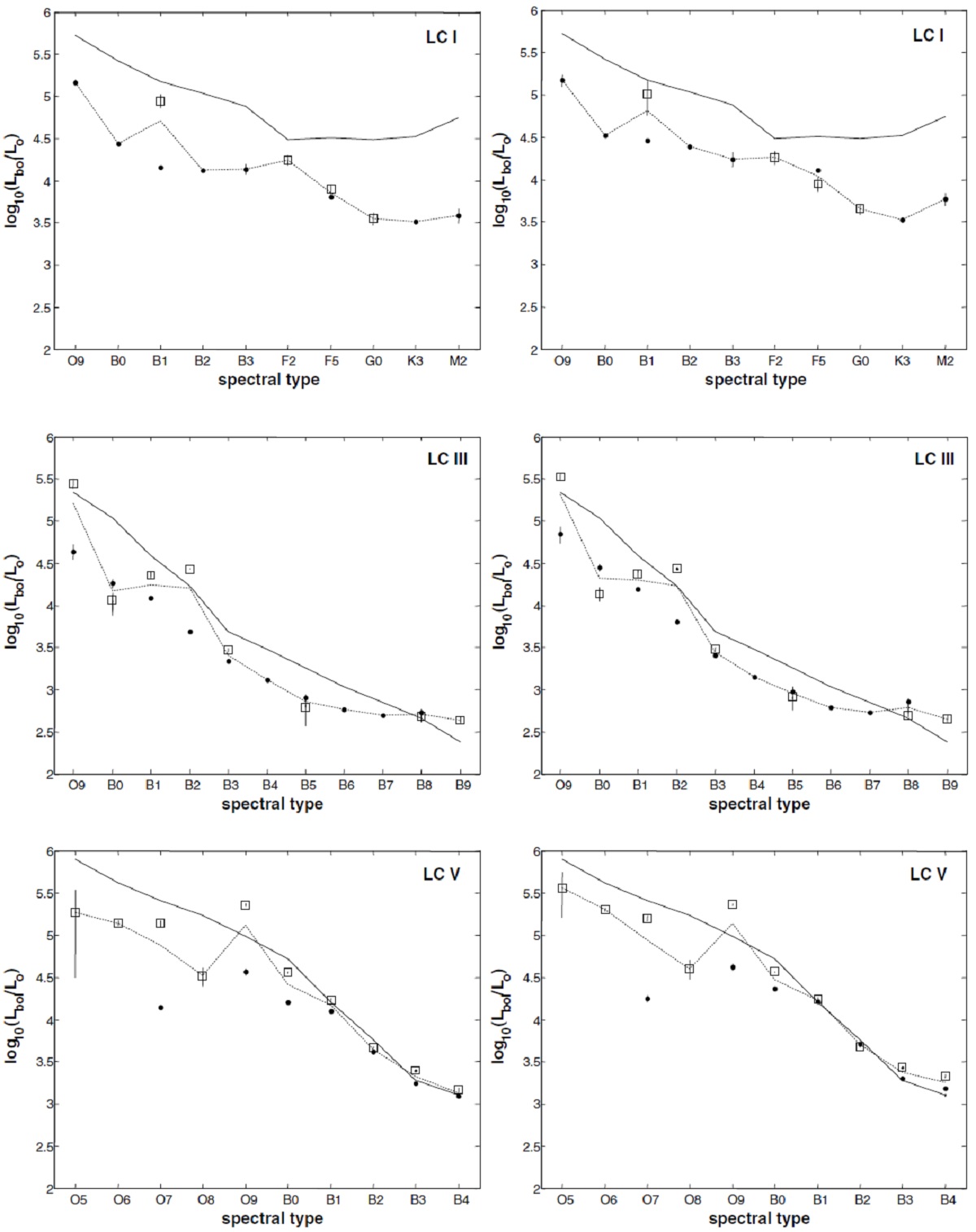
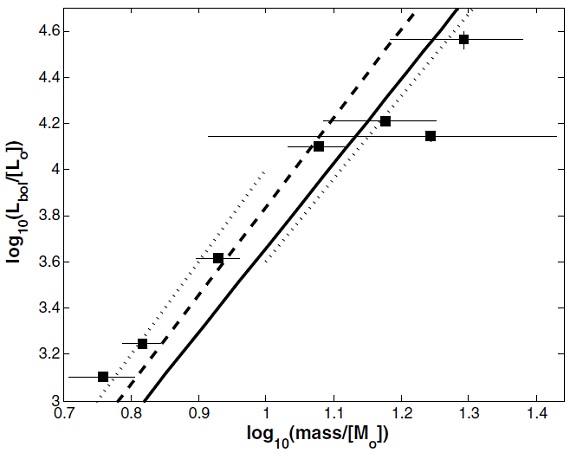 図9.黒四角=今回の質量光度関係。破線=Anderson et al 1991. 点線=Hilditch 2001。 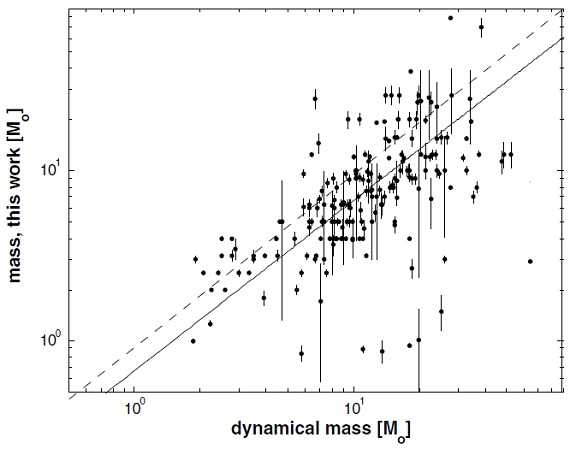 図10.黒点=連星の力学的質量と今回求めた質量の比較。 破線= one to one relation. 実線=黒点のフィット。今回の質量は力学 質量の 2/3 倍である。 質量の推定 光度と有効温度が分かったので、各星を HR-図上に置き、進化経路と比較 して質量を決めることができる。進化モデルには Schaller et al 1992, Bertelli et al 1994, Claret 2004 を用いた。計算結果を表3に示す。 スペクトルサブタイプと質量 各星の質量が求まったので、スペクトルサブタイプごとにまとめ、その 中間値を求めた。それらを表4に示す。光度と質量の関係は主系列星に対し、 L ∝ M3.66 となった。 |
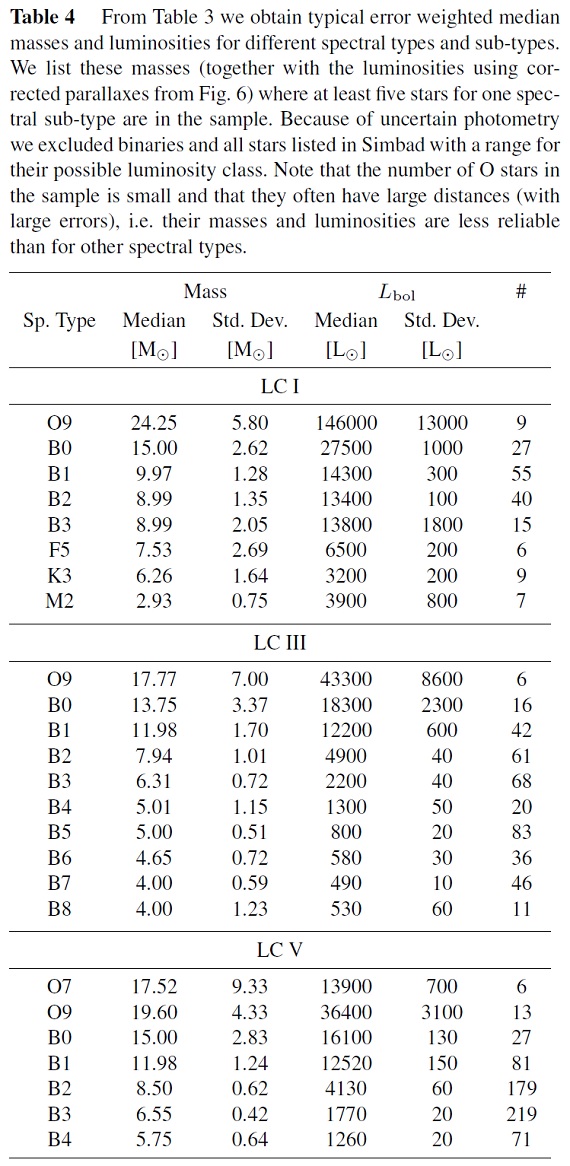 表4.表3に示す星質量をスペクトルサブタイプ毎にまとめた中間値 を示す。 |
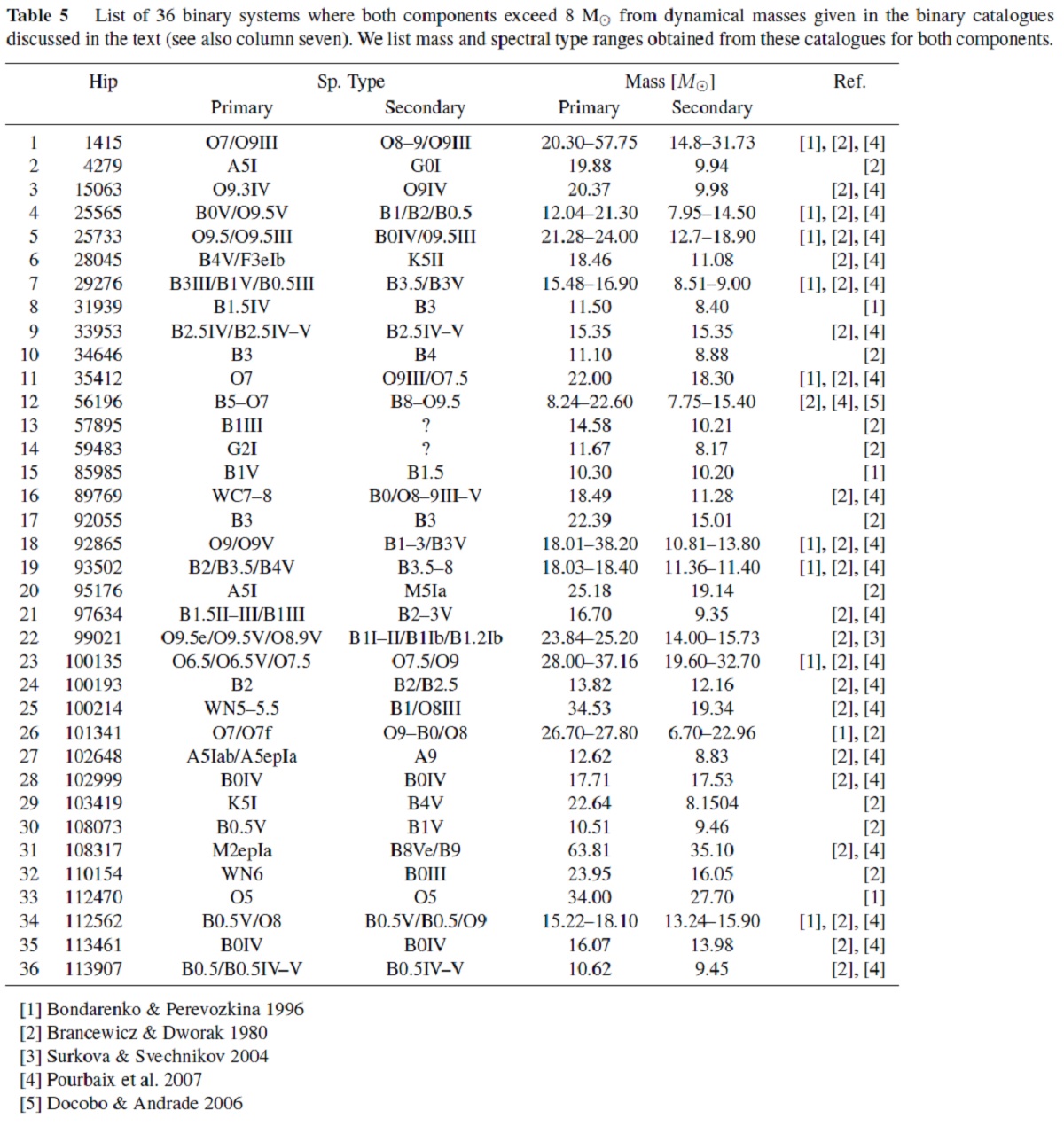
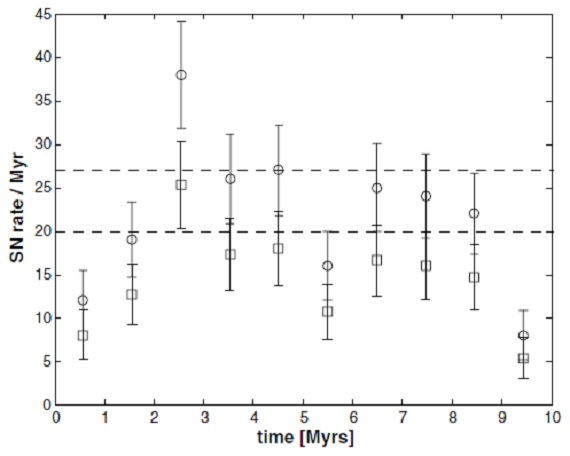 図12.丸=600 pc 以内の超新星爆発率。四角=それの 2/3 が Gould Belt 天体である。破線=Grenier et al 2000 によるGould Belt での 20-27 SNe/Myr. M > 8 Mo の星 759/2323 星が M > 8 Mo であった。内 36 個はより重い主星と連星を 成している。それらの連星系中3つの主星は M ≥ 30 Mo でブラックホール となる可能性がある。各サブタイプの中間質量とその周りの 1σ 分布を 考慮し、そのような星の数を計算した。600 pc 以内のそのような星の 2/3 は グールドベルトに属する。 超新星率 さらに恒星進化経路から決まる年齢と寿命から超新星爆発の時間も決まる。 このようにして、将来の超新星爆発率が計算できる。平均して 21 SNe/Myr という結果が出た。 抜け サンプルを 2MASS データアリに限ったので、最初は 3694 星 あったのが 2323 まで下がった。抜けがあり得る。600 pc 以内ではファクター 1.2 の違いがあるだろう。 |
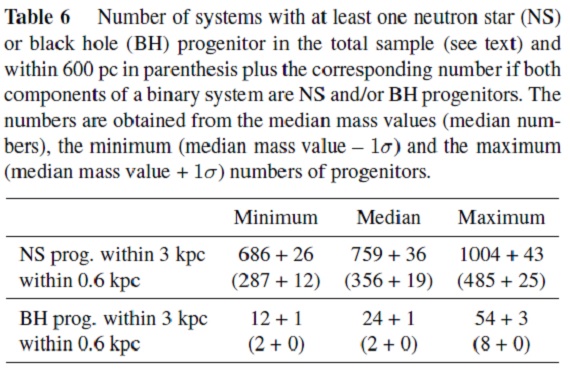 表6.中性子星かブラックホール前駆星になりそうな星の数。 |
|
範囲 我々のサンプル中 1536 星は 600 pc 以内にあり、 2127 星は 1 kpc 以内 にある。 光度 我々のサンプルの光度は」 Schmidt-Kaler 1982 の値より低い。 特に超巨星でそうである。その理由としては (1)以前用いられた地上観測からの距離よりヒッパルコス距離が小さい。 (2)以前単独星と思われていたが、連星と分かり主星、伴星に光度が分割。 |
質量 今回 HR-図上の位置から求めた質量は連星の力学質量と良い一致を示した。 超新星率 連星の内 36 星は M > 8 Mo である。それらから SN 率を求めると 1 SN/ 50kyr となる。 |