
| SDSS-III/APOGEE DR12 からの 69,919 赤色巨星を用い、 R = [3, 15] kpc, |z| < 2 kpc 銀河面内かってない体積での, [α/Fe] - [Fe/H] 面上 分布とメタル量分布関数を測った。内側円盤(R < 5 kpc) の星は、高アル ファ低メタルから始まり [α/Fe] = 0, [Fe/H] = 0.4 で終わる一本の [α/Fe] - [Fe/H] 系列をなす。より大きな半径では、[α/Fe] - [Fe/H] 空間に二本の系列が現れる:一本はほぼ太陽アルファでメタル量は一桁 の広がりを示し、もう一本は高アルファ系列で超太陽 [Fe/H] で低アルファ系 列と合体する。 |
高アルファ系列の位置は円盤全体で一定である。しかし、R > 11 kpc に
は高アルファ星が殆どない。円盤中央面 MDF のピークは R が大きくなると、
銀河系メタル量勾配を反映して、低メタル側に移動する。最も驚くべきは、
中央面 MDF の形が R と共に系統的に変わって行くことである: R = [3, 7]
kpc では負方向に片寄った分布だが、太陽円環付近ではガウシャン型となり、
外側円盤で正方向に片寄った分布となる。|z| > 1 kpc または [α/Fe]
> 0.18 では、MDF は R に依らず一定である。外側円盤 MDF が正方向に片
寄るのは動径移行 (migration) の標しかも知れない。軌道離心率は星種族のぼ
やけを」説明するには不十分であるが、動径移行の単純なモデルで説明できる
ことが判った。
(年齢データなしに「古い」、「若い」 と言っているのは解析姿勢が甘い。年齢の重要性を痛感する。) |
|
[α/Fe] - [Fe/H] の2系列 [α/Fe] - [Fe/H] 面上で太陽近傍星の分布は二つの系列を成す。 Furmann98, Prochaska00, Reddy06, Adibekyan12, Haywood et al. (2013), Anders14, Bensby14, Neidever14, Snaith et al. (2014). 一本は太陽[α/Fe] でメタル量の巾は広い。もう一本は低メタルで、 「Fe/H] = -0.5 まではほぼ一定の高い [α/Fe] を示すが、そこで折れ 曲がり [Fe/H] = 0.2 で太陽系列に合体する。この折れ曲がりは Ia 型 超新 星の出現によるらしい。 高アルファ系列 高アルファ系列星は大きなスケール高を Lee11, Bovy12 有し、厚い円盤種 族を構成する。Nidever14 は APOGEE レッドクランプカタログ Bovy14 を用 いて銀河面に渡って、[α/Fe] - [Fe/H] 関係を調べた。彼らは厚い円盤 に対応する高アルファ系列が彼らが調べた R = [5, 11] kpc の範囲でよく似 ていることを見出した。厚い円盤種族は短いスケール長と高いスケール高を 持ち、その運動は熱い。Bensby03,11, Allende Prieto06, Bovy12, Cheng et al. (2012), Anders14. しかし円盤が、厚い円盤と薄い円盤の多成分からこうせいされてい るのか、それとも円盤は連続的な種族系列 Ivezic08, Bovy12 なのか不明である。 低アルファ系列 Nidever14 は低アルファ系列の位置が銀河系内の場所により変化することを 見出した。内側円盤では高アルファ系列と低アルファ系列とが分離ではなくつ ながっている可能性がある。 MDFとG-型矮星問題 太陽近傍外での MDF の測定は APOGEE を使い ANders14 により初めて行われ、 銀河中心距離により変化することが見出された。 (唐突で文意不明) |
G-型矮星問題 Schmidt63, Pagel75 による閉箱化学進化モデルは観測より多数の低メタル星 を予想した。これは G-型矮星問題と呼ばれ Rocha-Pinto96, Schlesinger12, ガス降着 Pagel97 がその解答として提案された。MDF の観測は銀河系化学進化 においてはガスの運動が重要な役割を果たすことを明らかにした。G-矮星問題 が銀河系のどこにでも存在する問題なのかどうか、太陽円環の外側の観測が欠 けているため不明である。 (ここも論理が不明) 動径混合 シミュレイションモデルは内側から外側へモデル Larson76, Kobayashi11 や 上から下モデル Bournaud09, Bird13 が動径勾配や若い種族ほど低スケール高に なるなどの観測傾向を再現する事に成功している。 動径混合 動径混合の機構として "blurring" =離心率増加、と "churnin" = 半径増大 が提案されている。最近の観測から、太陽近傍の円盤構造は "blurring" だけ で説明可能 Snaith et al. (2014). と言われている。 APOGEE APOGEE は 3年間に 146,000 星の R = 22,500 分光観測を H バンドで行っ た。そこは減光強度が V バンドの 1/6 である。APOGEE の視線速度は 100 m/s の分解能を持ち、15 元素の組成を 0.1 - 0.2 dex 精度で求められる。 Garcia-Perez16. |

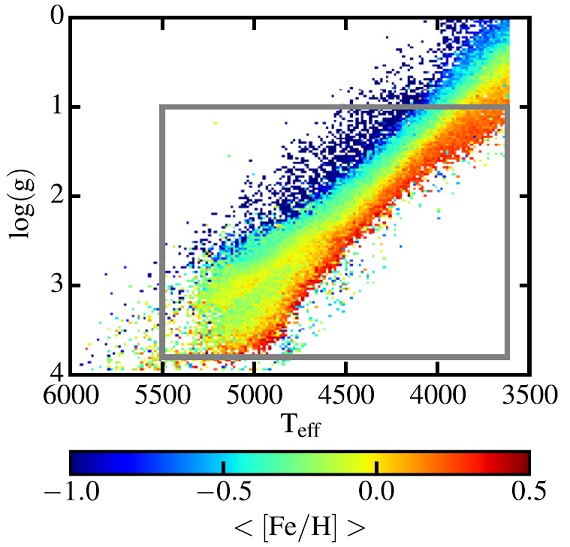 図1.APOGEE サンプルの分光学的 HR 図。各ビンの平均メタル量をカラーで示す。 灰色枠内にこの論文で扱う 69,919 星が含まれる。 APOGEE DR12 APOGEE は H = [8, 13.8] の観測を行った。減光補正は RJCE による。Zamora15 のスペクトルライブラリーペーパー 参照。ここでは Teff < 5500 K の巨星 log g = [1.0, 3.8] を表1のように 選んだ。図1には HR 図上のカット範囲が示されている。 アルファ元素 [α/Fe] は O, Mg, Si, S, Ca, Ti への全体的フィットから 求めた。 |
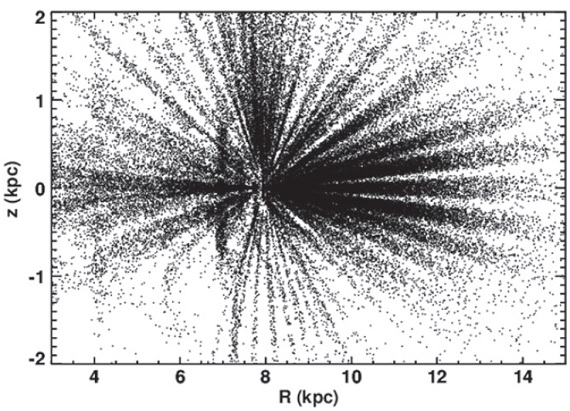 図2.APOGEE サンプル 69,919 星の R - z 図。各ビンの平均メタル量をカラーで示す。 灰色枠内にこの論文で扱う 69,919 星が含まれる。 種族バイアス 低温巨星をサンプルとしたために、古い種族に重みが掛かる。それは 寿命 τ に対し τ-0.6 Girardi01 である。しかし、 その補正は困難なので、年齢サンプルが一様でないことは許容して解析を 薦める。 |
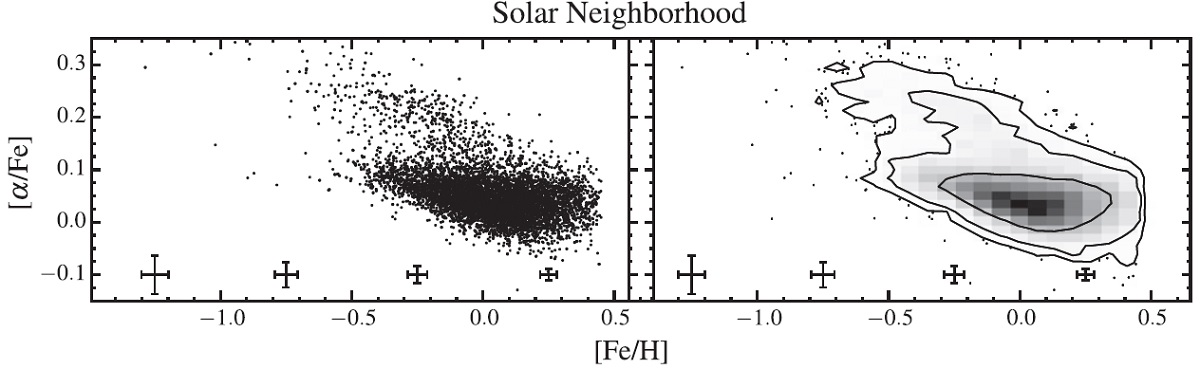
3.1.[α/Fe] - [Fe/H]図3=太陽近傍図3に太陽近傍 R = 7 - 9 kpc の [α/Fe] - [Fe/H] 分布を示す。 図4=色々な場所 図4=色々な場所の [α/Fe] - [Fe/H] 分布を示す。内側円盤 R = 3 - 5 kpc での最も著しい特徴は、低アルファ系列が消え、一本の 系列しか見えなくなることである。 | R = 5 - 7 kpc では二本系列が見えるが 低アルファ系列は太陽近傍より高メタルである。高アルファ 系列は R < 11 kpc に閉じ込められている。R > 13 kpc では大部分の 星は [Fe/H] = -0.4±0.2 の狭い幅に収まる。 |
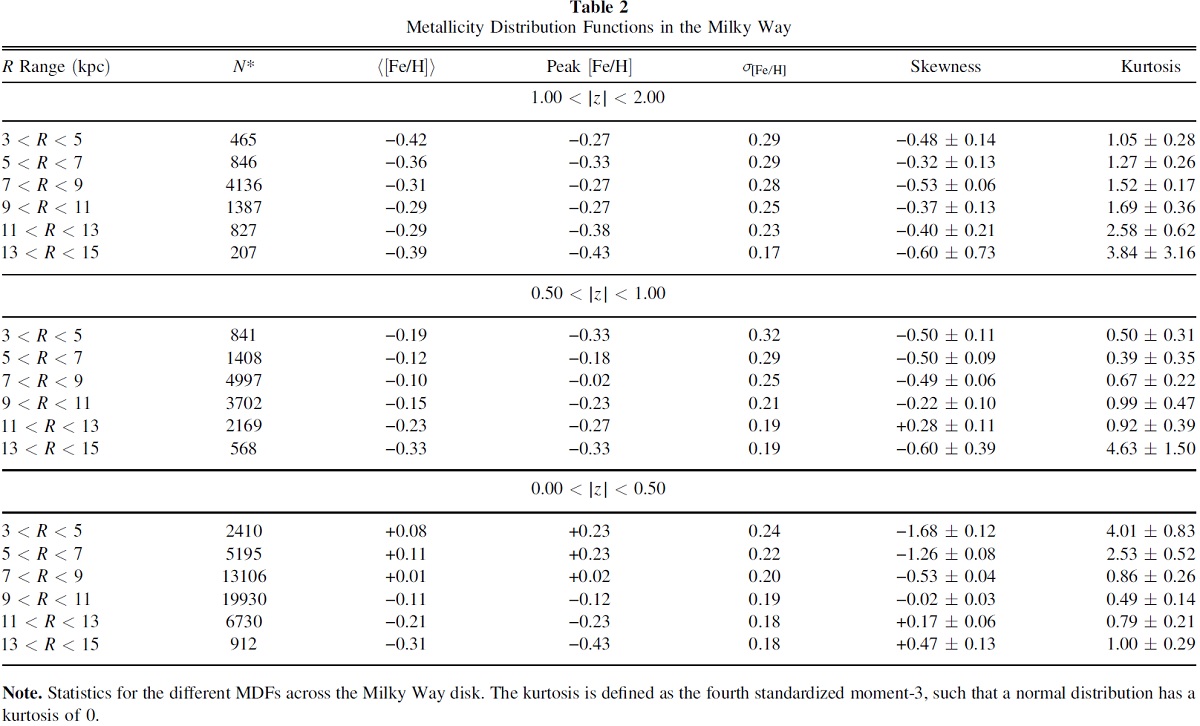

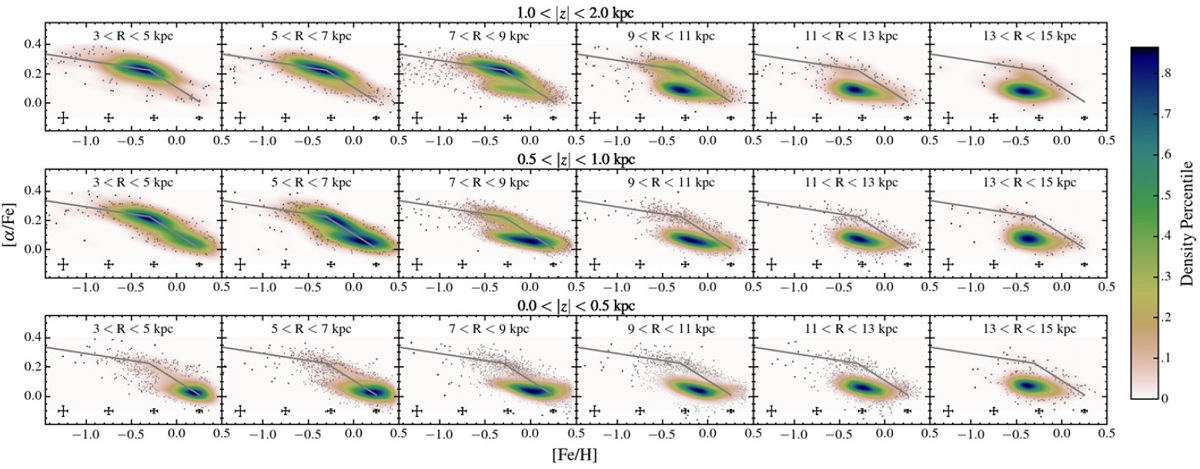
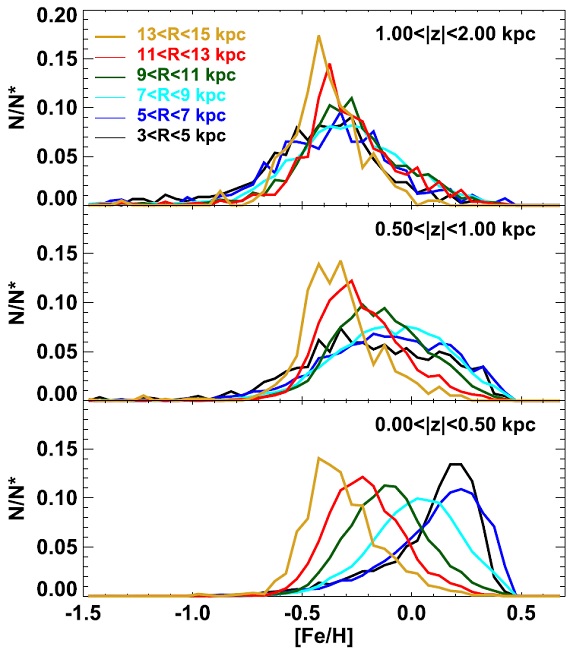 図5.R, |z| 区分ごとの MDF. 低 |z| 高度、内側 R = 3 - 5 kpc では負の側 に伸び、ピークは 0.25 dex である。外側 R > 11 kpc では正の側に伸び、 ピークは -0.4 dex に下がる。|z| > 1 kpc では MDF は R に依らない。 3.2.MDF中央面近くでの MDF 形状の変化図5には R, |z| 区分ごとの MDFを示す。下段、低 |z| 高度では円盤全体で 動径勾配が明らかである。R = 3 - 5 kpc では [M/H} = 0.32 と高く、太陽近 傍 R = 7 - 9 kpc では太陽メタルに近い [M/H} = 0.02、そして外側円盤 R = 13 - 15 kpc では [M/H} = -0.48 まで下がる。これらの特徴は既に以前の研究 Anders14, Hayden14 で得られていた。今回最も驚くべき発見は、 内側 R = 3 - 5 kpc では MDF が負の側に片寄り、外側 R > 11 kpc では正の側に片 寄るという MDF の形の変化である。 (ガウシャンを二つ重ねて片方のピークを 動かせばいいんじゃないか? ) |
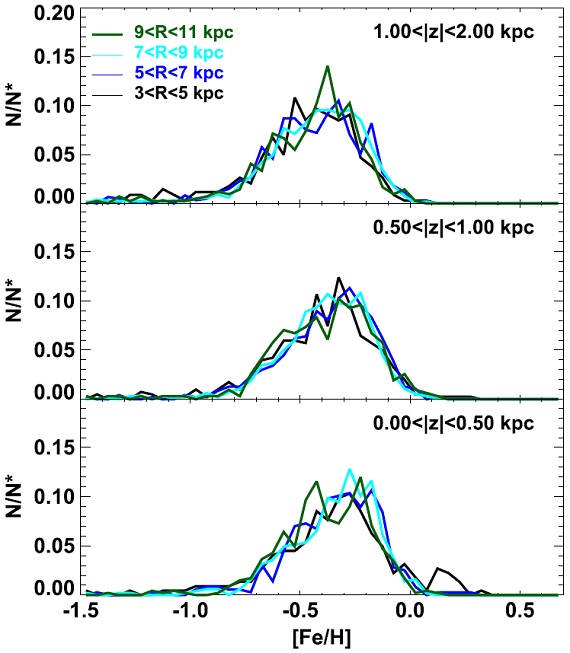 図6.[α/Fe] > 0.18 星の MDFs. R の差に依る違いはない。 僅かな |z| 効果は認められる。 高 |z| |z| が上がると、 MDF の R 変化は目立たなくなる。図5上段、|z| = 1 - 2 kpc では MDF は一様であるが、 R > 13 kpc ではピーク幅がせまくなる。 (これは言い過ぎ。ピーク位置は 明らかに動いている。R < 9 kpc は MDF 一定と言えるが、その先では動径 変化あり? ) 内側円盤の高 z では高アルファ星が支配的であるが、外側円盤 R > 11 kpc では低アルファ」星が支配的と変わる。[α/Fe] が変化するに拘わらず MDF が一様なのは驚きである。 (いや、変化してるぜ! ) 図6=高アルファ星の MDF 高アルファ系列は一様性が強い。そこで、図6に R と |z| の様々な区画で 高アルファ星の MDF を作って比較した。 (図5を高アルファと低アルファの足し算で 表せばいいのに。 ) 高アルファ MDF は銀河面近くではどの R でもピーク [Fe/H] = -0.3 で変わらない。 |z| が上がると、ピークが動き始め |z| > 1 kpc では -0.45 dex まで下がる。 |
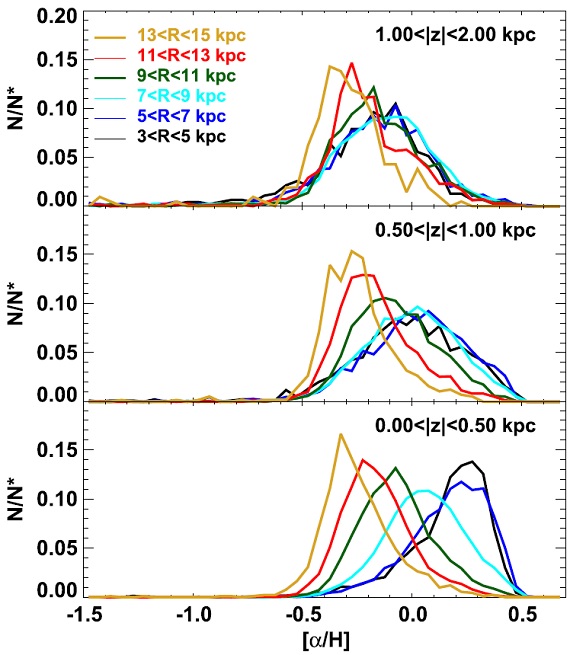 図7.R, |z| 区画ごとの全サンプルに対する [α/H] 分布(ADF)。 図7=[α/H] 分布 図7には R, |z| 区画ごとの全サンプルに対する [α/H] 分布(ADF) を示す。ADF は MDF と似ている。 |
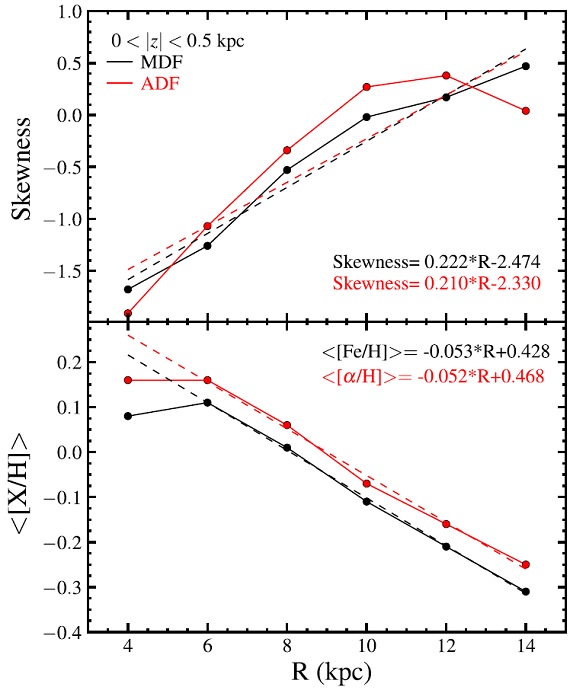 図8.上段:|z| < 0.5 kpc 星の動径距離 R による歪度(skewness) の変化。 R < 7 kpc では歪度が負で、 R が大きくなると 正に変わって行く。 下段:[Fe/H] と [α/H] の R による変化。二つの勾配は R < 6 kpc では似ている。 図8=[α/H] の変化 図8には[α/H] の変化を示す。 |
|
以前の結果の確認 以下は以前の研究で分かっていたことである。 a. 太陽近傍 MDF はガウス型 b. [α/Fe]-{fe/H] 面での分布は二系列 c. |z| が高くなると高アルファ星の比率が上がる d. 円盤中央面付近ではメタル量勾配がある。 発見 次の二つは今回の発見 e. 内側円盤 R = 3 - 5 kpc では [α/Fe]-{fe/H] 系列が一本で [Fe/H] = 0.4, 太陽[α/Fe] で終わる。 f. 円盤中央面付近では MDF の形が R により変化する。内側円盤では歪度が 負、外側で正となり、太陽円環はその切替わり点になる。 4.1.化学進化モデルとの対比Chiappini モデルChiappini et al. (1997), Chiappini01 は円盤を多数の円環に分けて、各円環にガスを2段階に降着させ て化学進化を計算した。第1降着は厚い円盤を形成し、高アルファ系列を産み 出す。ガス貯蔵が尽きると星形成が停止する。 |
第2降着はより穏やかで残ったガスを希釈し、メタル量を低下させる際に
SNe Ia が残ったガスの [α/Fe] を低下させる。 [α/Fe] は希釈
では値が変わらない。
(メタル量一時低下は観測結果?) ガスの表面密度が復活すると星形成が再開する。今度は低アルファ系列の低 メタル端からの出発となる。 Schonrich, Binney 2009 モデル Schonrich, Binney 2009 モデルは動径移行(migration) を考えた。彼らの モデルは MDF のピークが動径の強い関数で、内側銀河系が外側銀河系より高 メタルであることを示す。ピーク位置は APOGEE と似るが、 MDF の形はどこで もガウス的で APOGEE と異なる。また、彼らの [O/Fe] - [Fe/H] 図は APOGEE の [α/Fe] - [Fe/H] 関係とは似ない。 Kubryk et al 2013 シミュレイション Kubryk et al 2013 の粒子流体力学シミュレイションは円盤全体で一様な MDF を示す。MDF のピークは太陽に近く、負の歪度を示す。 Minchev et al 2013 の化学進化モデル Minchev et al 2013 の化学進化モデルは多くの観測事実と合う: [α/Fe] - [Fe/H] 関係、 |z| が上がると動径勾配が平坦化するなど。MDF の動径変化は 太陽近傍での APOGEE と似る。 |
4.2.1.Blurring (離心率増大) |
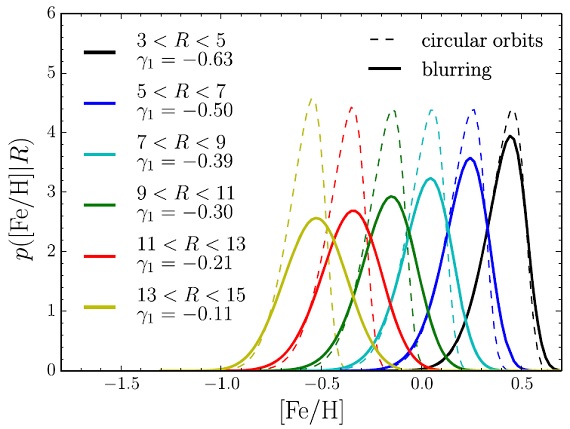 図9.破線=初期 MDF. 実線=blurring(離心率増加)の結果。歪度の符号が 逆転しない。 |
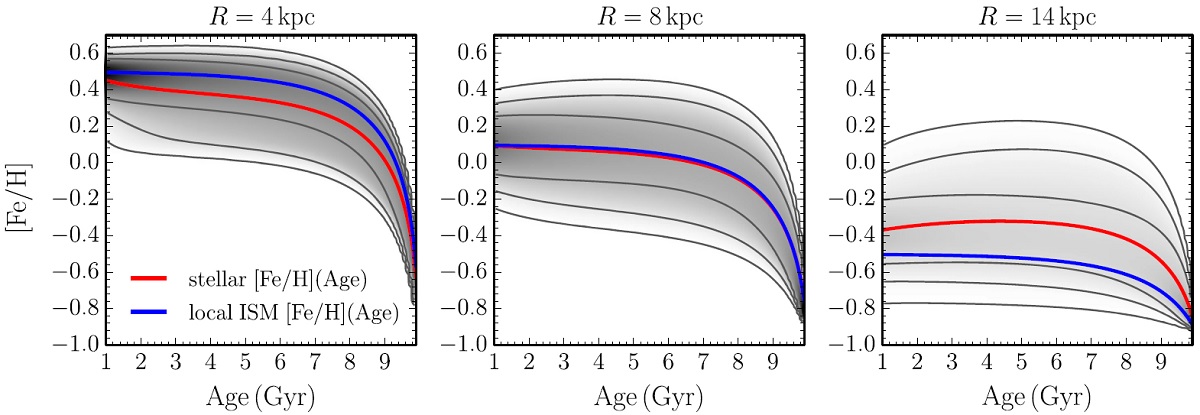
4.2.2.動径移行 |
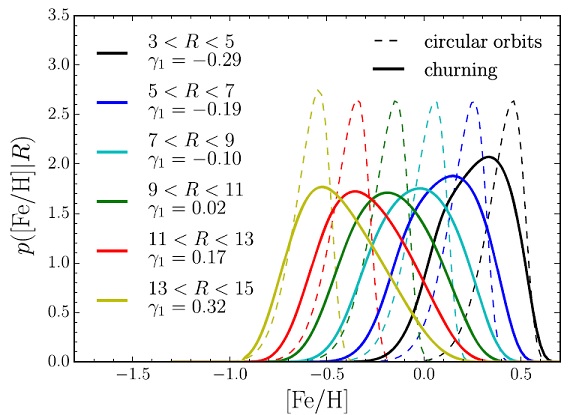 図11.破線=初期 MDF. 実線=blurring(離心率増加)とchurning(半径増大) を入れたモデルの MDF. churning による半径の再配分は歪度を産み出す。 |
|
|
|
1.内側円盤と外側円盤の違い 内側円盤と外側円盤は [α/Fe] - [Fe/H] 面で大きく異なる分布を 示す。内側円盤は一本の系列で表される。それは、高 [α/Fe] で始まり、 [Fe/H] = 0.5 で終わる。一方、外側円盤は高 [α/Fe] 星を欠き、主に 太陽- [α/Fe] 星から成る。 2.スケール高 内側円盤のスケール高は時間と共に低下した。古くて低メタル高アルファ な星は大きなスケール高を持ち、若くて高メタル低アルファ星は円盤中央面 に集中する。 3.MDF MDF のピークと歪度は円盤の何処かによる。 内側円盤の銀河中央面近くでは超太陽メタルであり、負の歪度を示す。外側円 盤は太陽以下のメタル量で正の歪度を持つ。 |
4.blurring(離心率増加)のモデル blurring(離心率増加)のモデルは MDF 歪度の観測を再現できない 5.churning(半径増大)はいい churning(半径増大)モデルは我々の観測に合う。 migration は円盤構造の 形成に重要らしい。 |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
