R Cen: An Unusual Mira Variable in a He-Shell Flush

　アブストラクト　

　１．イントロダクション　

　２．観測　

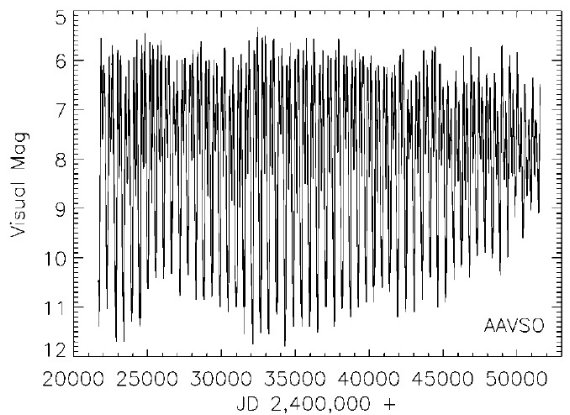
図１．R Cen の AAVSO 1918 - 2000 変光曲線。実線は 10 日平均をつないだ。 　R Cen の変光曲線　 　図１は R Cen の AAVSO 1918 - 2000 変光曲線である。これは世界中の 308 観測者による 13,857 観測の結果である。図はその一部 1980 - 2000 年の拡大図 である。深いのと浅い極小の間になじみ深い二重極大が見える。過去１０年間、 極小の深さが同じようになってきた。

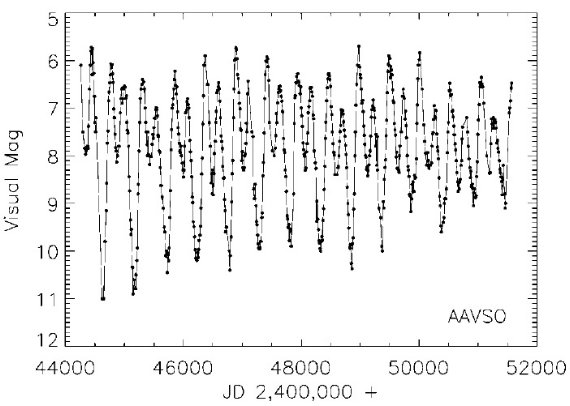
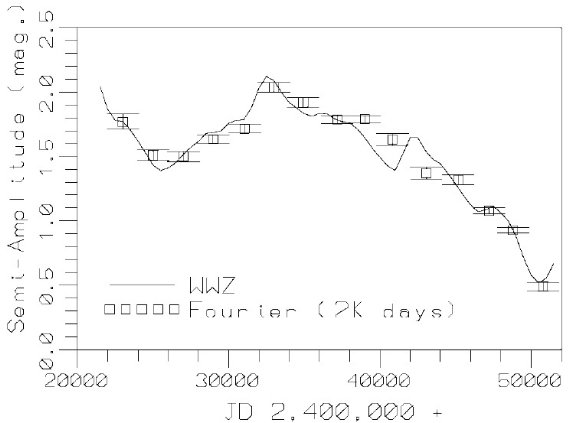
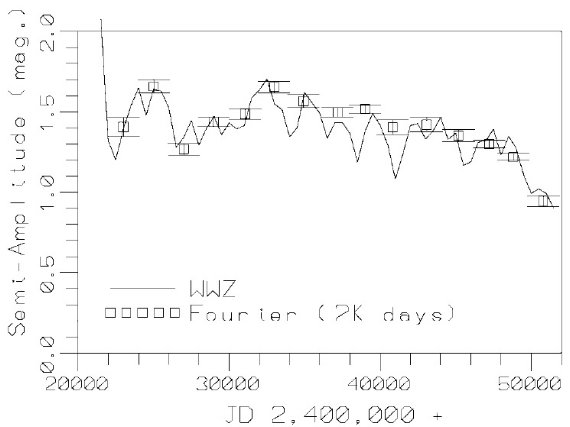
図２．R Cen の AAVSO 1980 - 2000 変光曲線。実線は 10 日平均をつないだ。 　変光振幅の縮小　 　変光曲線の異常な特徴は過去 50 年間、変光振幅が縮小してきたことである。 これは他のミラでも時々見られる。 Y Per は 1988 年に突然振幅 2.5 mag から 1 mag に変化した　Kiss et al 2000。V Boo (Szatmary, Gal, Kiss 1996) と RU Cyg (Kiss et al 1999) は振幅の漸減という R Cen と似た現象を示す。 セファイドでも北極星のように振幅が急変することがある。また、 R Cen では 1925 - 1940 に極小深さが変化した。

　３．パワースペクトル　

図３．R Cen のパワースペクトル。主モード f1 = 1/548 cycle/day を示す。 　フーリエ解析　 　R Cen の周期が変動しているので、周期が安定していた 1930 - 1966 年、 JD = 2,426,000 - 2,439,295 のデータを用いてパワースペクトル解析を行った。 解析には date-compansated discrete Fourier transform DCDFT (Ferraz-Mello 1981) と CLEANEST (Foster 1995) を用いた。通常のフーリエ解析はデータ点が 等間隔の場合には良い結果を与えるが、有限でランダムなサンプルでは大きな サイドローブを、データ点ギャップは偽のピークを生む。 　CEANEST アルゴリズム　 　CLEANEST はギャップのあるデータから真のピークを残すアルゴリズムである。 それは、ピークを一つづつ除いて調整する。説明が理解できなかった。 図３は CLEANEST を用いた R Cen のパワースペクトルである。多くのミラ型星 変光曲線は高周波成分を持つが、多くはピークの非対称性を表す役割を果たす。 しかし、R Cen　では第２高周波成分が異常に大きく、これが二重極大変光を 生み出す。 　パワースペクトルのピーク　 　表１に有意なピークを示す。これらは 548 d 主周期の高周波か、または 主モードの周りの衛星周波である。これらの衛星成分は徐々に変わる周期 の結果生み出された。

表１．R Cen のパワースペクトル

　４．ウェイブレット解析　

WWZ 法　 　周期が時間変動する現象を扱う weighted wavelet Z-transform = WWZ (Foster 1996) は周期や振幅が進化する現象の解析に適している。実際この ソフトは AAVSO を意識して作られた。データウェイトに 　　　　　W(t) = exp[-cω2(t-τ)2] を用いる。c = 0.0125 とした。 　小区間 CLEANEST 法　 　もう一つは、2000 d 区間毎に CLEANEST 法を適用して、小期間での周期、 振幅を決めて行く方法である。 図４a．第１モードの周期変化。実線＝ウェイブレット解析。四角＝小期間フーリエ解析。 図５a．第１モードの振幅変化。実線＝ウェイブレット解析。四角＝小期間フーリエ解析。

図４＝周期変化　 　こうして決めた周期と振幅の変化を主モードを図(a)に、第２モードを図(b)に 示す。図４a, b は JD 2,434,000 (1951) 以降第１、第２モードの周期が大きく 下降することを示す。その間、周期の比は 2:1 から１パーセント以内に収まっ ていた。 　図５＝振幅変化　 　図５から、第１、第２モードは共に大きく変化してきたことが判る。最近になると 第１モードの振幅は第２モードを下回るようになった。 図４b．第２モードの周期変化。実線＝ウェイブレット解析。四角＝小期間フーリエ解析。 図５b．第２モードの振幅変化。実線＝ウェイブレット解析。四角＝小期間フーリエ解析。

　５．議論　

周期変化と光度変化　 　図４は支配モードの周期が JD 2,434,000 (1951) での 550 d から 2000 での 505 - 510 d へと低下してきたことを示す。これは 1 d/yr = 3 10-3 day/day である。この結果を Wood, Zarro (1981) の質量固定での P-L 関係で解釈する。上記論文を再録すると、 （１）脈動の関係式 　　　C = P(M/Mo)α(R/Ro)-β （２）有効温度の式 　　　L = 4πσR2Teff4 （３）ＨＲ図の AGB を表式化 　　　log L/Lo = α - βlogTeff ( 熱パルス時の経路と異なるのが問題？) 上３式から、R と Teff を消去すると、与えられた M の下での、L-P 関係 が導かれる。 Wood, Zarro (1981) と同じパラメタ―、α=62.5, β=16.67, b=2, C=5.75 10-3 (d) を採用する。光度低下は主に周期変化で決まり、ＨＲ図上の経路勾配 β の影響は小さい。 ( 個々星に対する周期光度関係が 独立に求まる。距離の推定が問題。)

光度低下時期は？　 　R Cen の周期と光度の変化は R Hya より急である。この急さは、もし R Cen がヘリウムシェルフラッシュ直後の時期にあるとするなら理解できる。 Wood, Zarro (1981) の図１で言えば、Ａ点とＢ点の間である。ただし、中心核質量は 0.65 Mo 以下、 つまり星質量で 2-3 Mo 以下である。それ以上になると光度変化はさらに急と なってしまう。別の解釈としては、フラッシュの光度が表面に達しピークを形成 した後、図１のＣ点とＤ点の間も可能である。この場合は Mc > 0.6 Mo が 必要である。光度クラス II なので R Cen は低質量または高質量の超巨星で あり、独立な手法で質量が決まればヘリウムシェルフラッシュのモデルに制約を 与える。 　フラッシュと短期変動を区別する　 　R Cen が熱パルスサイクルのどの辺りにいるかを決めるには、更なる観測が 必要である。いくつかのミラ型星は周期が突然変化し、それが１０年または それ以上続く。ただ向きが逆である。その良い例は S Her と T Cep Wood, Zarro (1981) に見られる。これらの単期変動はヘリウムシェルフラッシュと似ていて、フラ ッシュやその他の長期効果を覆い隠す。したがって、長期の観察が必要なので ある。 　ヘリウムシェルフラッシュによる対流 が振幅低減の原因？　 　 R Cen の周期と振幅の変化は 1950 年頃に同時に起きているので、両者は 共にヘリウムシェルフラッシュに関連しているのであろう。振幅の縮小はフラ ッシュに伴って対流層が拡大したためかも知れない。強い対流は部分的または 完全に脈動を停止させると考えられる。それが RV Tau の対流二重極大モデル (Deupree, Hodson 1976) や S Per の脈動停止モデル (Kiss et al 2000) の 基となっている。 T UMi でも周期低下と共に振幅縮小が始まっている。 　ミラ型からセミレギュラーへの転移か？　 　もう一つの解釈は R Cen がミラ型星からセミレギュラーへと、つまり基本 振動から第１倍音へと、脈動モードが変わったと考えることである。図５の ウェイブレット解析は P = 510 - 550 d の主モードの振幅が過去 50 年間次第 に低減してきて、今では 274 d モードを下回ることを示している。

　６．結論