Age Calibration and Age Distribution for Rich Star Clusters in the LMC

　アブストラクト　

　２．年齢較正　

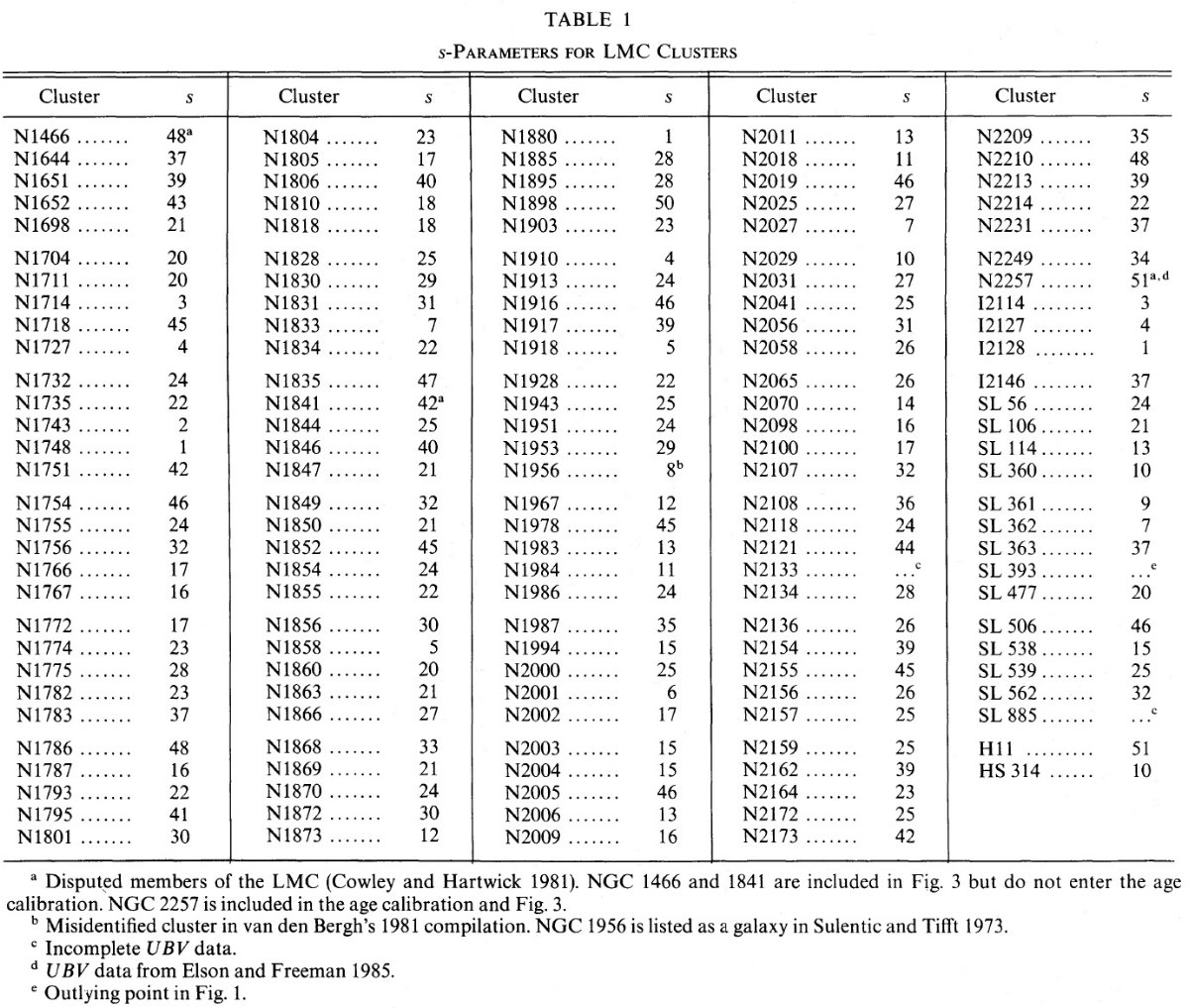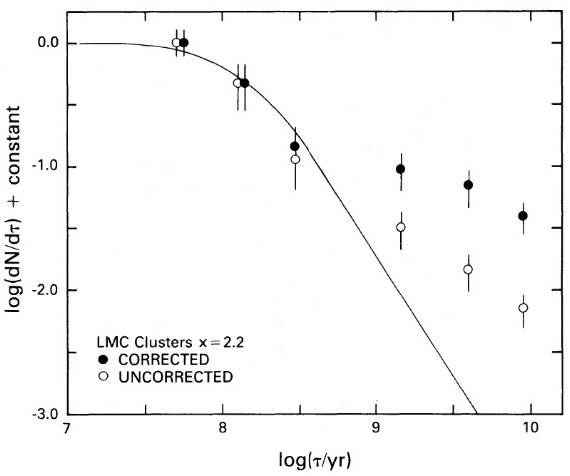
図１．星団 UBV 二色図。黒丸＝ LMC, 白丸＝SMC. U-B と B-V は van den Bergh 1981 の集めたデータから採った。実線上の目盛＝年齢パラメタ― s. 長い棒＝ SWB タイプの近似的な区分け。L79 と SL393 は系列から外れていて、 s-パラ メタ―は付かない。矢印は E(B-V) = 0.1 に対応する赤化ベクトル。 　ＵＢＶ測光の得失　 　 Searle, Wilkinson, Bagnuolo (1980) は、積分 ugvr 測光から導いた二つの減光フリー指数に基づき、マゼラン雲の 大星団を７種に分類した。 SWB タイプは一次元の系列をなし、彼らはそれを 年齢が増加すると共にメタル量が減少する効果として解釈した。基本的に同様 の関係が UBV 二色図にも現れる。UBV 測光は SWB タイプの決まる星団の 3 倍はある。減光フリーではないが、マゼラン雲の減光は E(B-V) = 0.1 程度 で、しかもその大部分は銀河系内成分である。数千万年程度の年齢の若い星団 を除くと、E(B-V) は平均から 0.1 以内に収まり小さい。多くの目的には 赤化による結果の不定性より、サンプル数の多さの方が大事である。 　SWB タイプと年齢　 　SWB タイプを年齢と結びつける試みは、これまであまり良い結果を産んでい ない。最近では Hodge 1983 が主系列ターンオフから導いた星団年齢が、各 SWB タイプ内で一桁の散らばりを持つことを示した。我々はより細かい区分と より多くの星団で再挑戦する。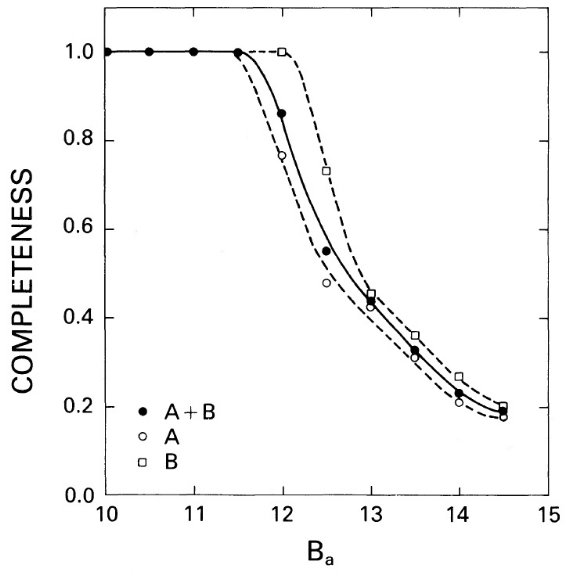 　SWB タイプと s-パラメタ―　 　図１には van den Bergh 1981 が集めた UBV データをプロットした。NGC 2257 だけは Elson, Freeman 1985 から採った。図中には SWB 系列に倣った曲線を 引いた。この曲線からのズレは測光エラー ±0.1 mag の程度である。 この系列を同じ長さの 51 区間に分割した。その区間の番号として s パラメタ― を定義する。表１、２にはその値を示した。s-パラメタ―と SWB タイプを比較 すると、LMC 星団の 90 %, SMC の 70 % が s-パラメタ―で正しく SWB タイプ に分類された。これは s > 35 のフック部でもそうである。

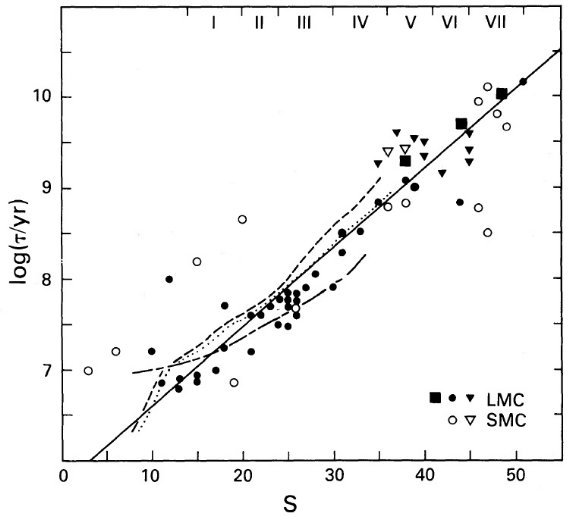
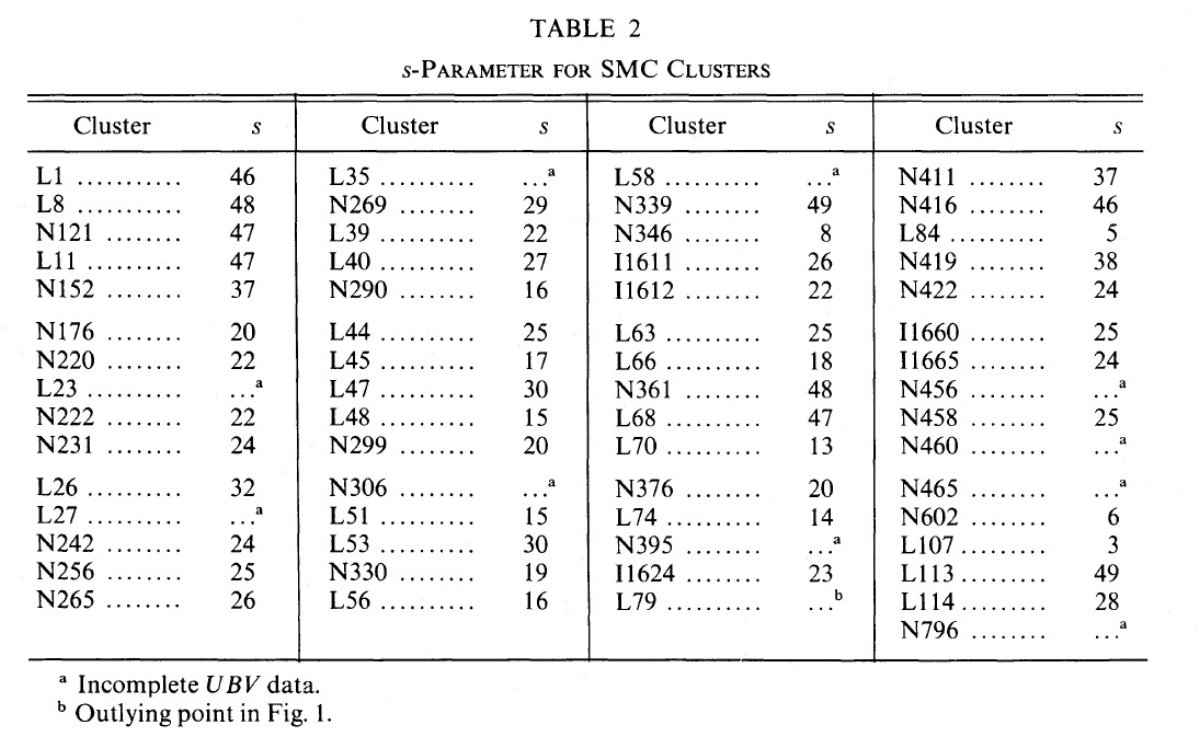
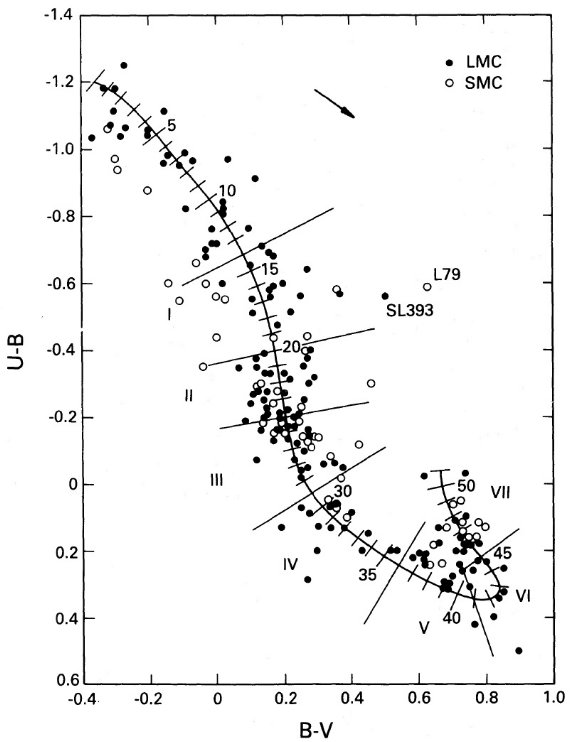
図２．年齢パラメタ― s の較正。黒丸＝ LMC, 白丸＝SMC. U-B と B-V は van den Bergh 1981 の集めたデータから採った。実線上の目盛＝年齢パラメタ― s. s は図１から求めた。年齢 τ は、丸＝ Hodge 1983 の主系列ターンオフ。 四角＝ Searle 1984 の積分スペクトル。三角＝ Mould, Aaronson 1982 の AGB 測光。直線＝ LMC 星団の式 (1) の最少二乗フィット。破線 = Searle, Sargent, Bagnuolo 1973 の恒星種族モデルの x = 1.1 IMF. 点線＝ x=2.2 IMF モデル。一点破線＝ Dixon, Ford, Robertson 1972 の太陽近傍 IMF. 上横軸は SWB クラスの大体の区分。 　s - τ 較正　 　図２には log τ と s の関係をプロットした。τ の出所は、 (a) ターンオフ LMC 33, SMC 14 Hodge 1983 は当時得られていた色等級図を全て集めて、それを Schlesinger 1969, Stothers 1972, Brunish 1981 の等時線と比較した。最近の等時線と大 きく違わない限り、Hodge の τ を採用した。NGC 1831 は Hodge 1984, NGC 1856 は Hodge, Lee 1984, NGC 2134 は Hodge, Schommer 1984, NGC 2162 は Schommer, Olszewski, Aaronson 1984, L8 (=K3) は Rich, Da Costa, Mould 1984, L113 は Mould, Da Costa, Crawford 1984 から採った。 (b) 積分スペクトル　16 LMC, 0 SMC Searle 1984 は SWB タイプ V, VI, VII のバルマー線と金属線の等値巾と 星団年齢を関係させた。較正は較正種族モデルの合成スペクトルと年齢、メタ ル量既知の銀河系星団のスペクトル観測との比較でなされた。 (c) 炭素星　9 LMC, 2 SMC Mould, Aaronson (1982) は AGB 先端付近の星の赤外カラーから星団年齢を推定した。 残念なことに、二つ以上の方法で星団年齢が決められた例が見つからない。 しかし、図２を見ると、 log τ と s にはほぼ直線の関係が存在する。 最小二乗法でこの関係をフィットすると、 　　　log (τ/yr) = (0.087±0.004)s + 5.77±0.12 となる。標準偏差は 0.3 である。この関係式は SWB タイプに関して Fall, Frenk 1983 が導いた、 　　　log (τ/yr) = 0.5(SWB クラス) + 6.6 と合う。 　種族モデルとの比較　 　Searle, Sargent, Bagnuolo 1973 は IMF の傾き x = 1.1, 2.2 (x=1.35 が サルピータ　IMF)、太陽組成で種族モデルを作った。それらも図２に示す。 Searle73 と Dixon72 モデルの差は主に恒星内部構造に起因する。モデル不定性 を考えると、モデルと s の一致は良い。低メタルになると勾配が寝るので それも SMC の観測に合う。

　３．質量限界　

図３．年齢パラメタ― S とアパーチャ光電等級（van den Bergh 1981 の収集） の関係。 黒丸＝ LMC, 白丸＝ SMC. s は表１，２から。上枠の τ は式１ から。破線＝ Searle, Sargent, Bagnuolo 1973 の x=1.1 モデル。実線＝ x 2.2 モデル。 　減衰ラインによる質量分離　 　　144 LMC 星団の年齢を得たが、星団は様々な目的の研究から集められて 来たので、星団年齢分布を直接表してはいない。まず質量限界サンプルを 作製する必要がある。図３には van den Bergh 1981 が収集した光電測光 V データを示した。測光アパーチャに星団の光が全部入るわけではないので、 この値は V でなく Va とした。図３には種族モデルの V 等級減衰ラインも示す。 カラーは IMF 勾配の影響を大きく受けなかったが Va の方はモデルによる変化 が大きい。 x が小さくなると、完全性補正後の古い星団数はより大きくなる だろう。 　減衰ラインの問題点　 　減衰ラインによる質量分離には様々な難点がある。 （１）アパーチャ等級と全等級との差が等級で変わる。 （２）種族モデルは太陽組成だが、 LMC では [Fe/H] = -0.3 (SWBI-V) - -0.7 (SWB VI), -1.3 (SWB VII) (Cohen 1982, Searle 1984) （３）マスロスの影響 （４）星の逃散 （５） IMF 勾配の不定性 しかし、それでも等級限界のような規準よりは年齢分布を決めるには適している。 　星質量の巾　 　Searle, Sargent, Bagnuolo 1973 は ML = 0.25 Mo, MU = 35 Mo とした。図３の減衰線に対応する質量は x = 1.1 に対しては 5 103 Mo, x = 2.2 では 1.1 104 Mo である。

図４．van den Bergh 1981 の LMC 星団 UBV 収集の完全度。A, B は領域名。 実線は図５、７での完全度補正に使用。 　完全性の補正　 （１）Hodge-Wright 1967 アトラスの領域 A と B にある星団を同定した。 等級は 8インチ f/1 シュミットカメラを使い、フィルターなしの IIIaJ 乾板写真を眼視で定めた。±0.4 mag 程度の精度が期待される。また、 星団検出は B = 14.5 mag まで完全と看做せる。 （２）van den Bergh 1981 の星団を領域 A, B 内で等級帯毎に数え、上の 星団数と比較して完全度を算出した。

　4. 年齢分布　

図５．星団質量限界サンプル(x=2.2)の年齢分布。黒丸＝図３の完全性補正。 白丸＝補正なし。実線＝ Wielen 1971 の 太陽から 1 kpc 以内の星団年齢分布。

図６．銀河系内散開星団の年齢分布。バツ＝0.5 kpc 以内。黒丸＝ 1 kpc 以内。 白丸＝ 2 kpc 以内。実線＝ Wielen 1971 の 太陽から 1 kpc 以内の星団年齢分布。

図７．銀河系 R < 1 kpc 散開星団の年齢分布。バツ：リッチネスクラス R = [0, 2]。 白丸： R = [3, 5]. 黒丸：LMC 星団。 実線＝ Wielen 1971 の 太陽から 1 kpc 以内の星団年齢分布。