The Initial Mass Function for Massive Stars

　アブストラクト

　１．イントロダクション　

　２．O-型星カタログ　

２．a. データ源　 　サンプル　 　サンプルの多くは Cruz-Gonzales et al 1974, Humphreys 1978 から 来た。それに加え、Garrison, Kormendy 1976, Garrison, Hiltner, Schild 1977, Feinsteinm Marraco, Muzzo 1973, Feinstein, Marraco, Forte 1976, Moffat, Fitzgerald, Jackson 1979 のデータを用いた。 星団メンバーシップの同定には Conti, Alschuler 1971, Moffat, Vogt 1975 を用いた。スペクトル分類には Garrison, Hiltner, Schild 1977 を用いた。カタログは ADC から得られる。 　カタログ項目　 　カタログには HD, BD, 星団メンバー、V, B-V, スペクトル型、l, b, を載せた。星団・アソシエイションメンバーでない星はフィールド星とした。 絶対等級は Conti 1975 のスペクトル型による較正を用いた。 Av = 3 E(B-V) で減光を定めた。温度スケールには Conti 1975 を、輻射補正は Morton 1969 を用いた。 　スペクトル分類　 　カタログには 781 個が載っていた。内、50 個は UBV カラーがない。 140 は スペクトル型はあるが光度クラスがない。この 140 個の再分類観測が 進行中である。 　２． b. 完全度　 2.8 kpc までは完全度が高い　 　図１には距離に対する O-型星の累積個数を示した。2.8 kpc までは 累積個数は距離に対し、指数 2.3 のべき乗則に従うことが分かる。これは 不完全性の影響が 2.8 kpc から先で現れてくることを意味する。 ただし、腕などの非一様な成分の影響があるのでこの見積もりは不確かである。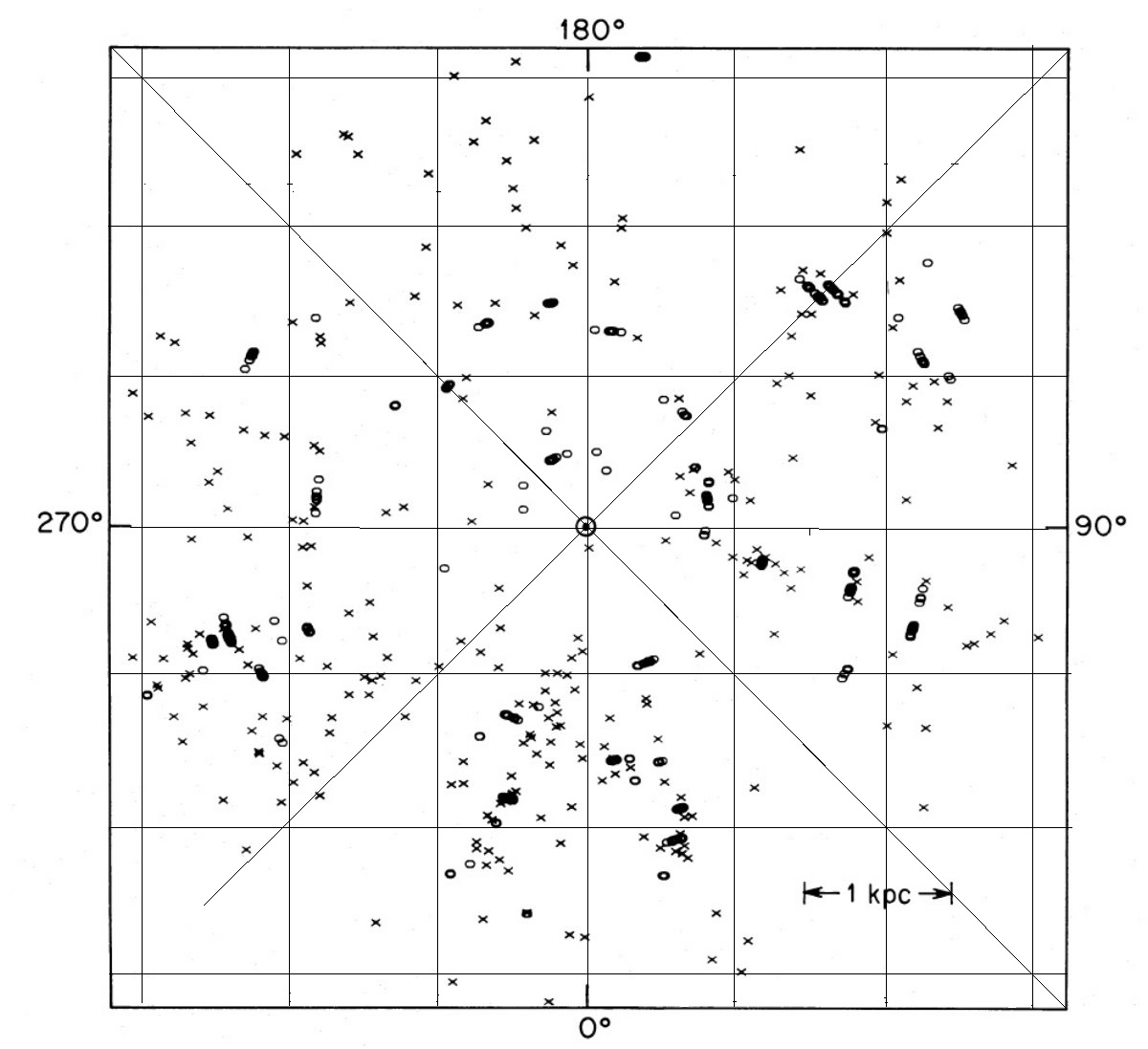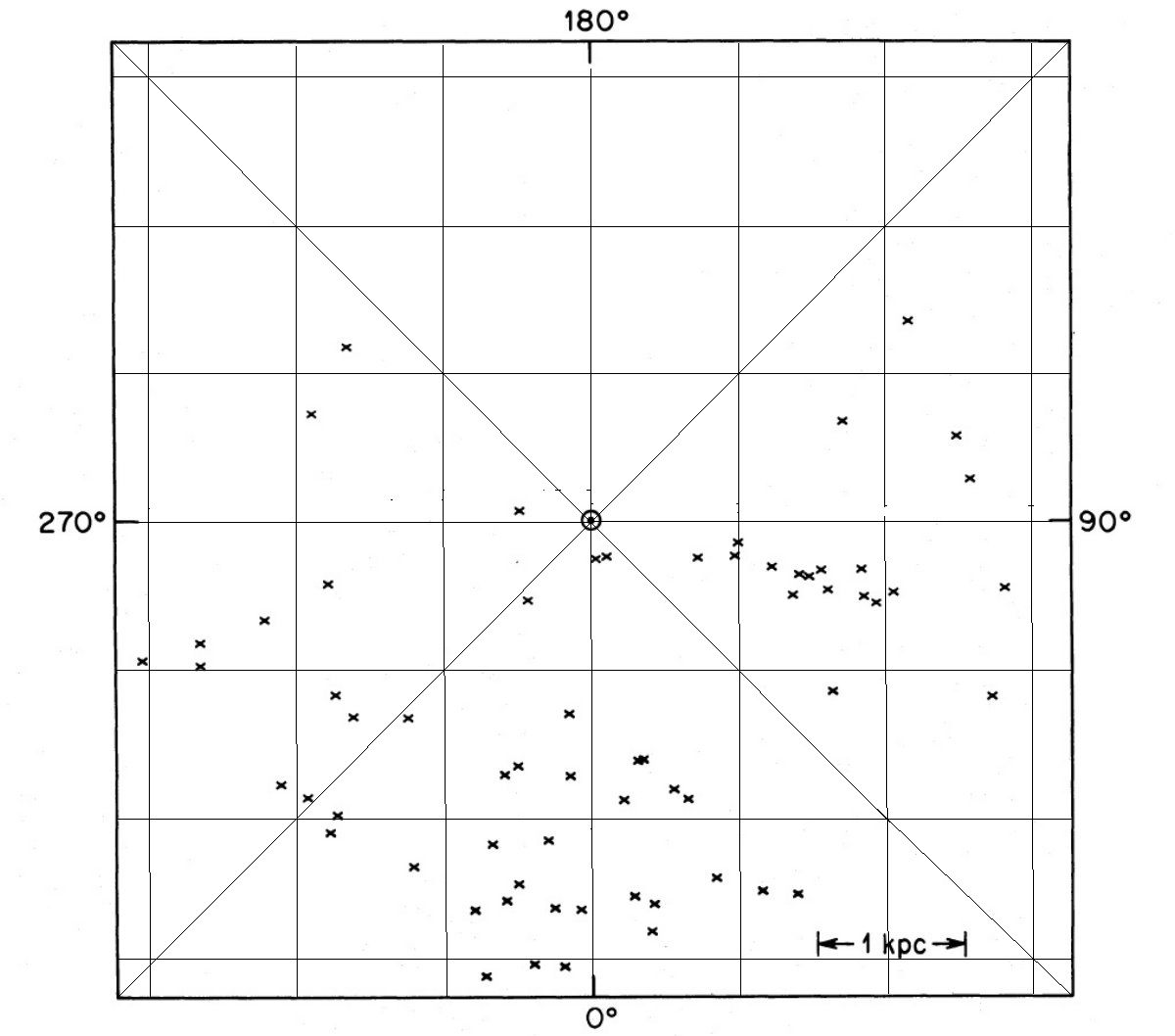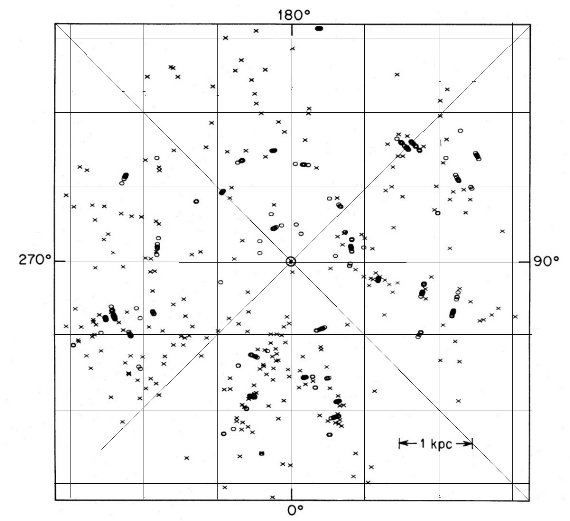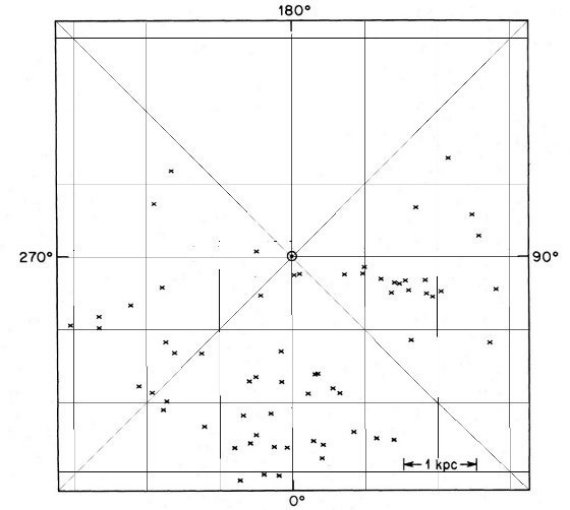 　腕が見える　 　図２の銀河面上分布を見ると、腕の影響が大きいことが分かる。図から アソシエイションを除いても腕の形が見えるので、フィールド O-型星の距離は 比較的良く決まっており、つまり、これらは Carrasco et al 1979 のいう ような古い種族星ではないことを示している。 　分子雲内の星　 　分子雲内の星はカタログから逃れている可能性がある。しかし、どのくらいが 雲に埋もれているかは分からない。

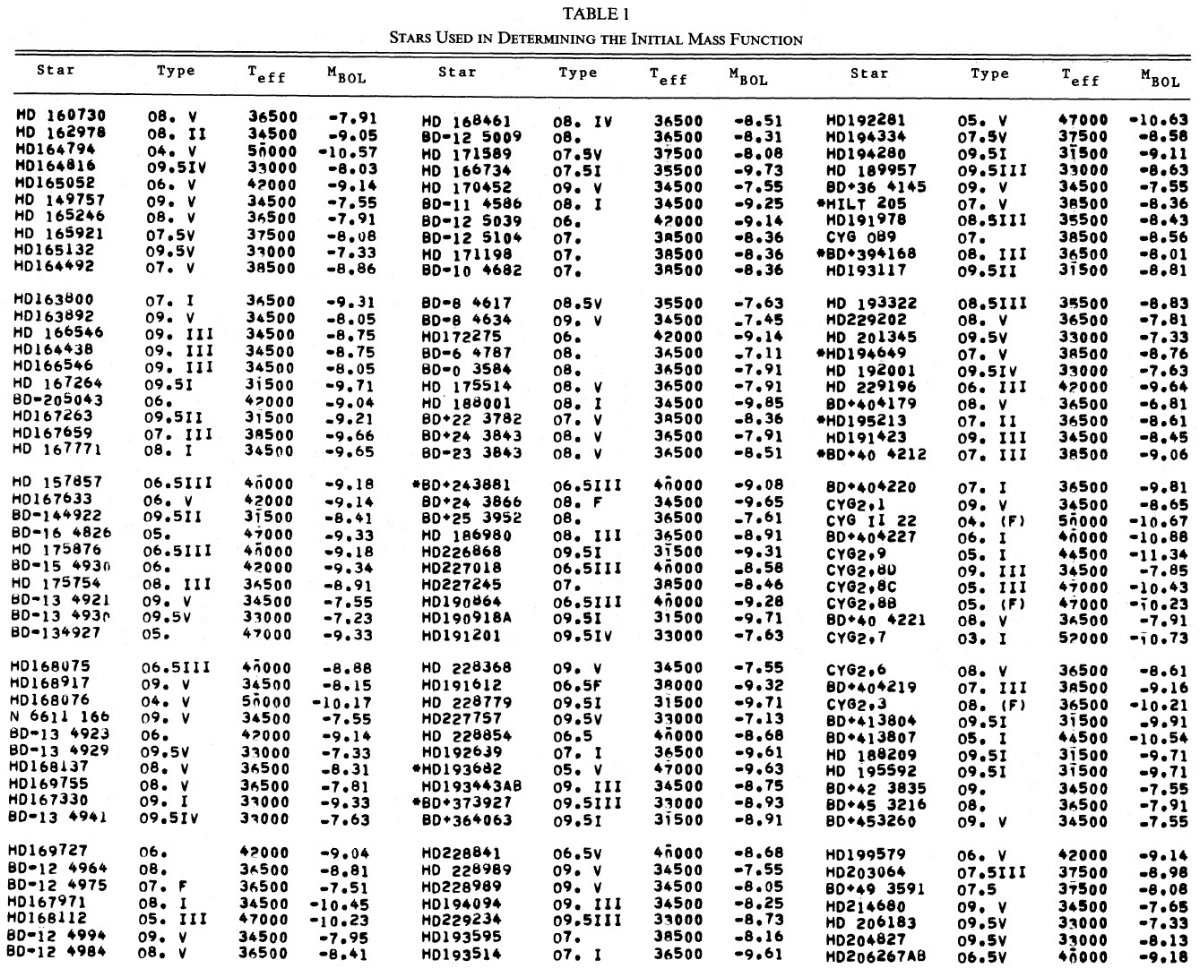
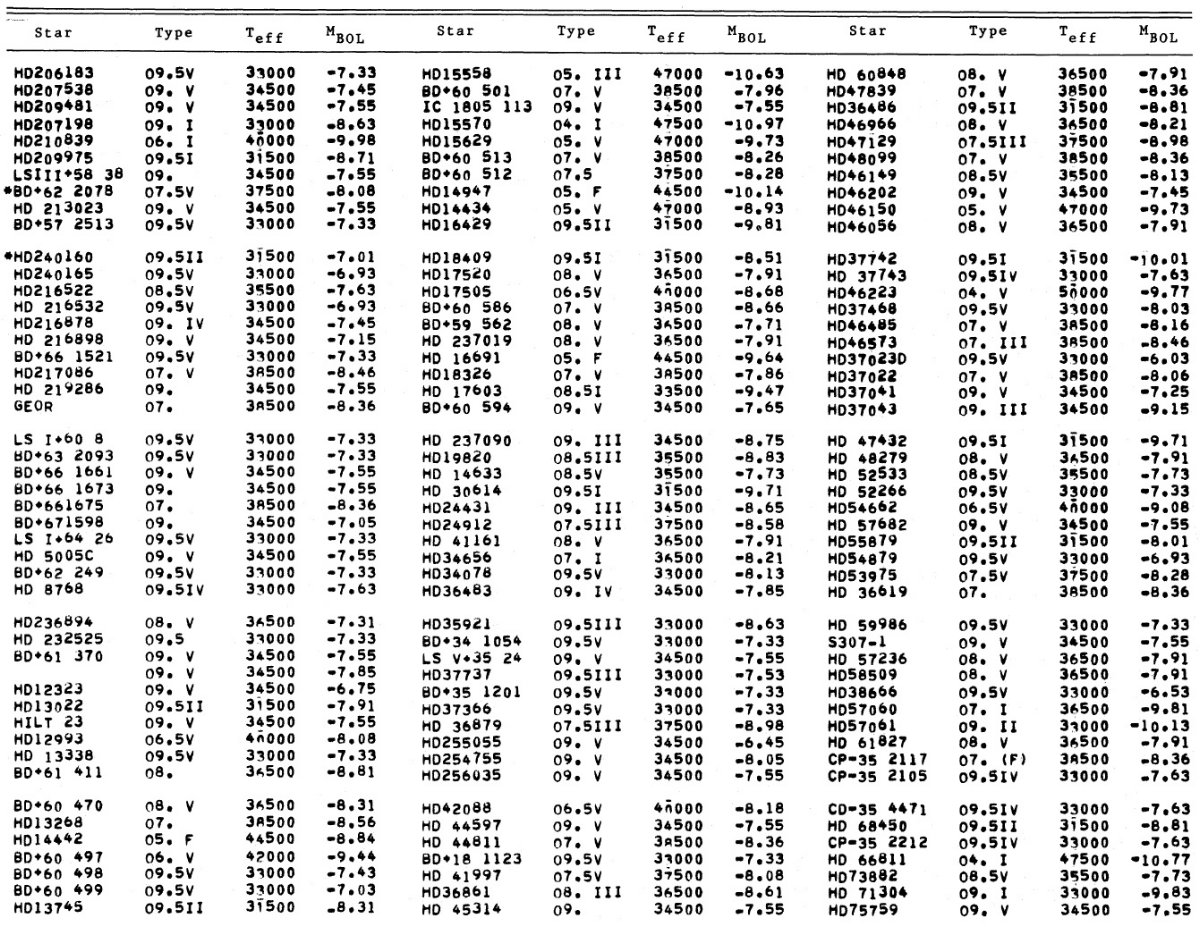
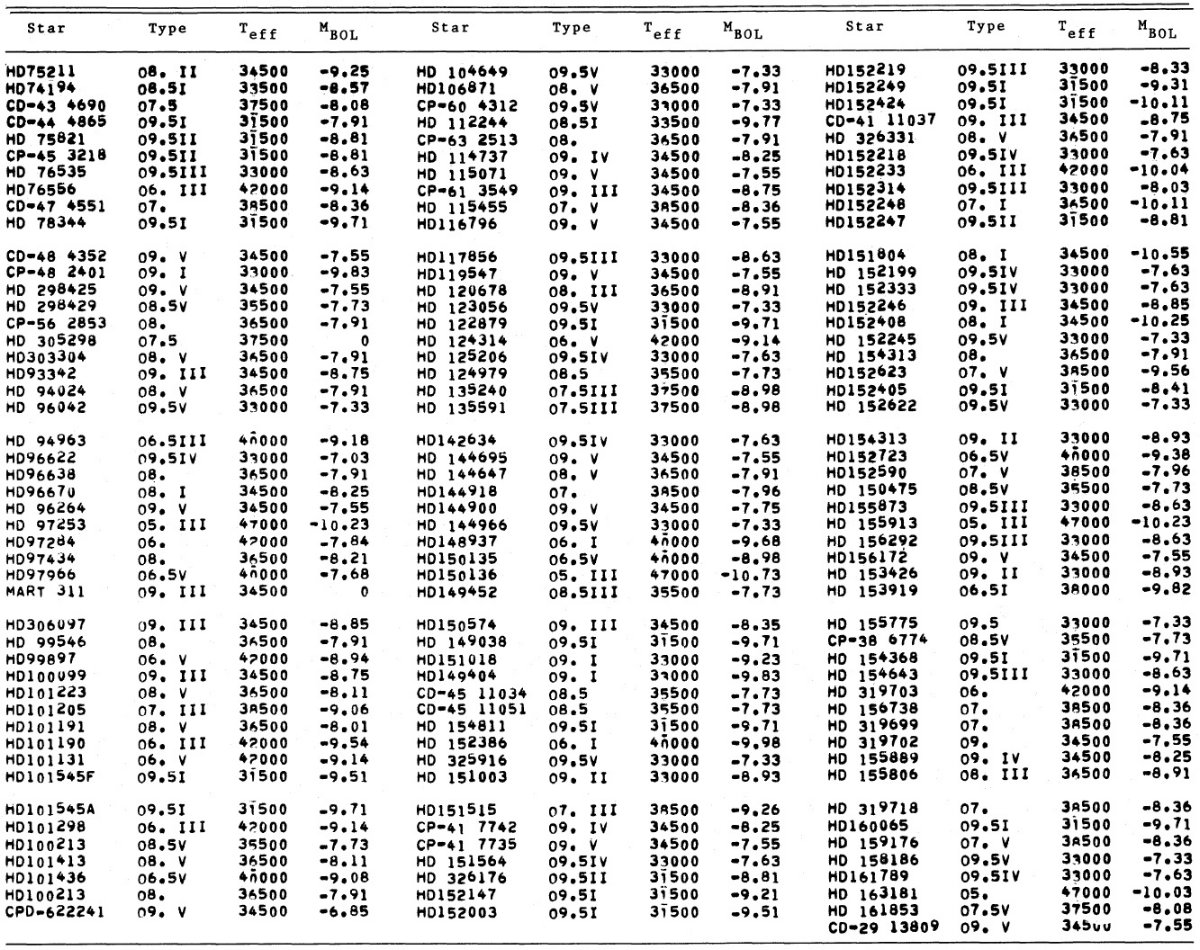
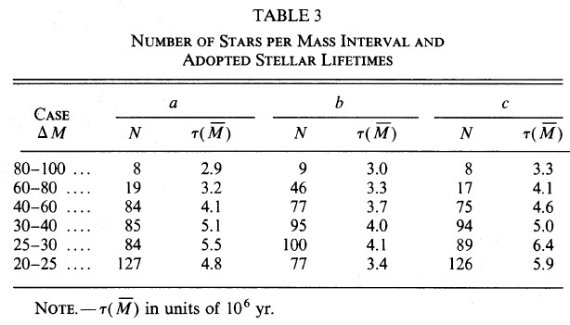
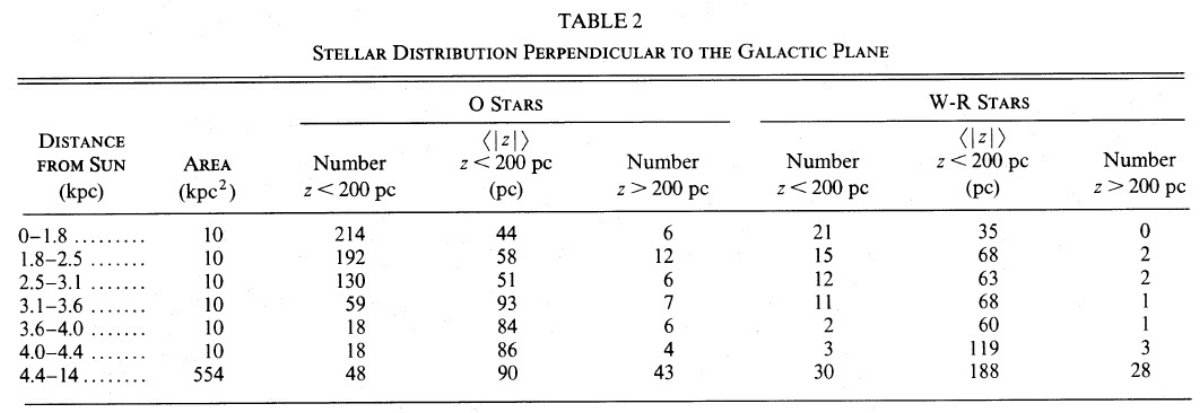
光度クラス　 　IMF には光度クラスが必要であるが、2.5 - 2.8 kpc のクラスター O-型星には この情報が欠けているものが多い。したがって、 IMF の解析には 2.5 kpc までの 星を用いる。それらは 424 星であり、表１に載せた。 36 フィールド星には (B-V) または光度クラスが欠けている。しかし、結果を大きくは変えない。 　平均　Z　 　まず銀河面と直交する分布を見てみよう。表２から銀河面から 200 pc 以内の星の 銀河面距離の平均値は太陽から 3 kpc 以内では一定で、その先増加していく。これは 銀河面に近いほど検出不完全度が高くなるためと考える。したがって、 O-型星の 平均 Z 距離は 45 pc と考えてよい。 　高 Z 星　 　では、Z が 200 pc より大きい星ではどうだろう？ 2,5 kpc 以内にはそのような 星が 18 個ある。内 5 個は暴走星である。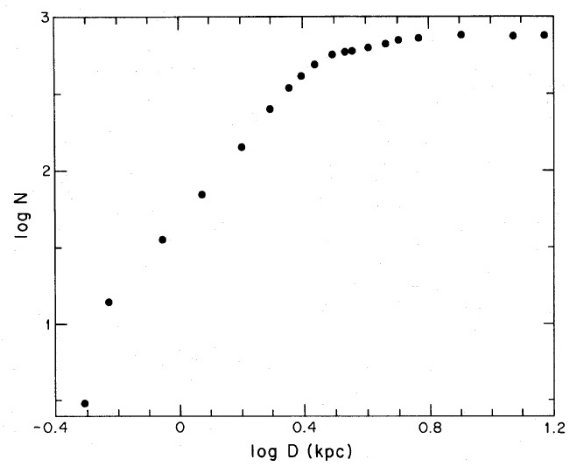 図１．距離に対する O-型星の累積個数。0.6 - 2.8 kpc の間勾配は 2.3 で データの完全度が高いことを示す。

　表１．IMF を作るのに使用した星　
１次資料に絶対等級、距離が載っていたらそのまま使用。 星団・アソシエイションに属していたらその距離を使用。
フィールド星の絶対等級は Conti 1975 のスペクトル型ーMv 関係から決めた。

　表２．銀河面と直交方向の O-型星分布　

　３．初期質量関数　

３．a. 初期質量関数の導出　 　、Mbol - Teff 図を作った　 　表１のデータを用いて、Mbol - Teff 図を作った。図３がそれである。 標準的な Mv, B.C., Teff 較正をフィールド星に対しても行い、そのため、 固まりあい効果が生じ、H-R図は滑らかでなくなっている。観測 H-R 図の 下限縁とモデル ZAMS との一致はきれいである。 　Sct OB2 と Cam OB2 の距離　 　ただし、Sct OB2 と Cam OB2 に属する 8 星は ZAMS より 0.4 mag 程度下に来る。 これは二つの距離(Humphreys 1978) が小さく与えられているからではないか？ 　モデル進化経路　 　比較用に３種類の進化経路 X=0.7, Z=0.02 を作った。吸収係数は Cox,Stewart 1970 を用いた。 （a）質量一定。 （b）輻射圧マスロスあり。ケース α=0.98 （c）マスロス＋オーバーシューティング 　進化経路で決まる区間星数　 　３つのどれもコア水素燃焼期の経路は図３の範囲より低温度側まで伸びる。 そこで、O-型から B-型までたどり着くまでの時間を寿命として用いること にした。考えている中で最小質量の星を除いて、これは水素燃焼全期間の 80 - 100 % をカバーする。質量区間内の星の数（これは区間端に対応する 進化経路に挟まれた領域内の観測星数？）と区間寿命は三つのケースごとに 表３に載せてある。 　IMF の定義　 　IMF には色々な定義があるが、ここでは 　　　　　ψ(M) = dN/dlog M = A M-B とする。単位は、stars kpc-2 yer-1 (log M/Mo)-1 である。

図３．2.5 kpc 以内 O-型星のモデル HR-図。有効温度は Conti 1975, 輻射補正は Morton 1969 を使用。黒点＝単独星。黒丸＝ 6 - 10 星。黒三角＝ 11 - 19 星。 黒四角＝ 20 - 40 星。長破線＝マスロスなしの進化モデル。短破線＝マスロスあり （Chiosi, Olson 1981)。実線＝対流核オーバーシューティング(Bressan et al 1981)。 モデル初期質量＝ 100, 80, 60, 40, 30, 25, 20 Mo.

IMF の作成　 　表３の値を ψ(M) と合わせて決めた A と B を表４に示す。 モデル毎に差が付いた理由は、 （１）寿命が違う （２）質量区間がカバーする HR-図上の領域が違う ためである。図４には、得た IMF を Miller,Scalo 1979 と　 　 Lequeux 1979 の IMF と比較した。 表３．質量間隔に対応する星数と寿命。 表４．IMF パラメタ―　A, B。

図４．太陽から 2.5 kpc 以内の O-型星 IMF . 単位は、stars kpc-2 yer-1 (log M/Mo)-1. 実線＝表４の組み合わせ。一点鎖線＝ Lequeux 1979 の IMF を O-型準矮星を入れた場合 と除いた場合について。点線＝ Miller, Scalo 1979.

　４．BC - Teff 関係が IMF に及ぼす影響　

Boem-Vitense の Teff　 　我々は Conti 1975 のスペクトル型対有効温度関係と Morton 1969 の 輻射補正を用いて IMF を導いた。 ( 本文ではあまり触れられていないが、 絶対等級の決定方法も大事だと思う。) Bohm-Vitense 1981 はスペクトルタイプと Teff の関係をレビューした。彼女の Teff はここで採用した Conti 1975 の Teff よりかなり低い。図５には Teff(Voem-Vitense)　と Morton の B.C.(Teff) を使って作った 2.5 kpc より 近い O-型星の HR-図を示す。図には Bressan, Bertelli, Chiosi 1981 のZAMS と 進化経路も載せた。最高光度ではZAMSとその後の進化状態にある観測星に比べ、 モデルは高温で両者の一致は悪い。この不一致は、（１）計算を見直すか、（２） ZAMS は観測にかからないとみなすか、と考えることもできる。 　Stothers, Chin 1977 の計算　 　Stothers, Chin 1977 は Carson 1974 の新しい吸収係数を使って計算し直した。 しかし、この吸収係数の正しさに関しては疑問がある。 　ZAMS は見えないのか？　 　Mezger 1976 は ZAMS 期間は数 Myr で母分子雲が散逸する時間とほぼ等しく、 星が可視光で見えるようになるまでに中心部の核反応はかなり進行してしまっている と考えた。したがって、これら大質量星は ZAMS を離れるまで目に触れないのである。 図５を見ると、最青の星のラインは、大質量星(M> 25-30 Mo) は全て 2 Myr 以上 の年齢であることを意味している。これが分子雲が蒸発する時間 &tau:E に相当するかどうか現時点でははっきりしないので IMF に関してはフリーパラメタ― として扱う。 　分子雲が蒸発する時間 &tau:E　 　分子雲が蒸発する時間 &tau:E は 1 - 3 Myr であろう。ケース(c) について、 幾つかの &tau:E に対して決まるパラメタ― A, B を表５に載せた。予想される 通り、 &tau:E の増加に伴い IMF は平坦になっていく。表６には Ni = 見えない星と Nv = 見える星の比率 Ni/Nv を &tau:E の関数として示した。 Ni/Nv は 0.2(&tau:E=1Myr) から 1.3(&tau:E=3Myr) へと変化する。 この数字は M = 25 -80 Mo の星について積分して求めたもので、 25 Mo はその先で 雲に隠れている星の数の割合が無視できないほど大きくなる質量である。 　赤外天体　 　表６を見ると、O-型星の 20 - 50 % は分子雲内部に埋もれている。それらは 赤外観測でのみ検出可能である。 &tau:E = 1 Myr は　 　 Mezger 1976 の結果と一致するが、赤外調査はまだ予備的段階である。しかし、このシナリオなら Bohm-Vitense の低い有効温度と折り合いがつく可能性がある。これは将来の 重要な課題であろう。 表５. Bohm-Vitense の低い Teff を採用した時の IMF パラメター A, B と 分子雲蒸発時間の関係。

図５．Teff(Voem-Vitense)　と Morton の B.C.(Teff) を用いて作った、 2.5 kpc 以内 O-型星の HR-図。破線=Bressan et al 1981 の進化経路。一点鎖線 ＝ 1 Myr と 2 Myr 等時線。太い破線＝Stothers,Chin 1977 が Carson 1974 吸収係数を用いて計算した mixing length parametaer λ=2 のZAMS. 表６．M = 25 - 80 Mo 星の表面密度と分子雲散逸時間の関係。

　５．W-R 星の問題　

図２（縮小）．O-型星の分布 　５．a. W-R 星の進化シナリオ　 　Conti 1976 シナリオ　 　O-型星がマスロスを起こして WR-星に進化する。ただし、マスロスのメカニズムは 幾つかの説があり、確定していない。 　５．b. W-R 星の銀河面上表面分布　 　絶対等級　 　WR-星は分光的に発見が容易であるが、絶対等級の較正が出来ていないので 距離が決まらない。図６には Sixth Catalog of Galactic Wolf-Rayet Stars (van der Hucht et al 1981) に基づき、Hidayat et al 1981 が再計算した WR-星距離を プロットした。彼らは WR-星の検出は 5 kpc まで完全であると考えている。 距離の不確かさに拘わらず、渦状腕パターンが見えていることに注意。 　５．c. W-R 星の銀河面上表面分布　 W-R 星の分布が銀河中心方向に集中　 　Roberts 1962 は　W-R 星の分布が銀河中心方向と反中心方向で大きく差があること を報告している。2.5 kpc 以内の W-R 星は太陽円外側で４個、内側で 31 個である。 　O-型星 IMF の銀河中心と反中心方向での差　 　太陽円内側 IMF は 　　　　　ψ(M) = dN/dlog M = 1.1 10-3 (M/Mo)-1.3 　太陽円外側 IMF は 　　　　　ψ(M) = dN/dlog M = 8.4 10-3 (M/Mo)-2.1 二つの大きな違いは、内側ではカリーナ, シグナス方向に 40 Mo 以上の大質量星が存在する 事である。これは、内側渦状腕における最近の星形成爆発を反映しているのであり、 IMF が銀河中心距離により真に変化するのとはちょっと違うのかも知れない。

図６（縮小）．WR-星の分布。 図７．太陽円の内側と外側での IMF.　四角＝太陽円内側。丸＝太陽円外側。 点線＝ Miller,Scalo IMF.

　６．まとめ