An Analysis of the Shapes of Interstellar Extinction Curves IV. Extinction without Standards

　アブストラクト　

　１．イントロダクション　

　２．減光の決定　

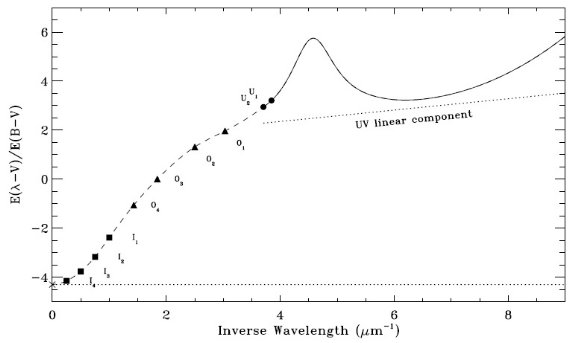
２．１．ペア法　 　ペア法　 k(λ-V) = E(λ-V) m(λ-V) - m(λ-V)o E(B-V) (B-V) - (B-V)o 二つの星を同じ装置で観測する場合の利点は装置等級をそのまま使用できる ことにある。しかし、欠点が二つある。一つは赤化ゼロの標準星は少なく スペクトル型がとびとびになることである。このため不適合な組み合わせが 避けられない。二つ目は赤化ゼロと言える早期型星が少ないことである。 このため減光の修正を行うがエラーを生む。 　スペクトル型不適合の影響　 　図１は不適合が減光曲線にどんな影響を持つかを示す。スペクトル型不適合 は O-型星ではより深刻である。赤化の小さな O-型星は殆どないので、 スペクトル型不適合な組み合わせで減光を決めるしかない。さらに進化の進んだ 明るい星は問題がより大きい。

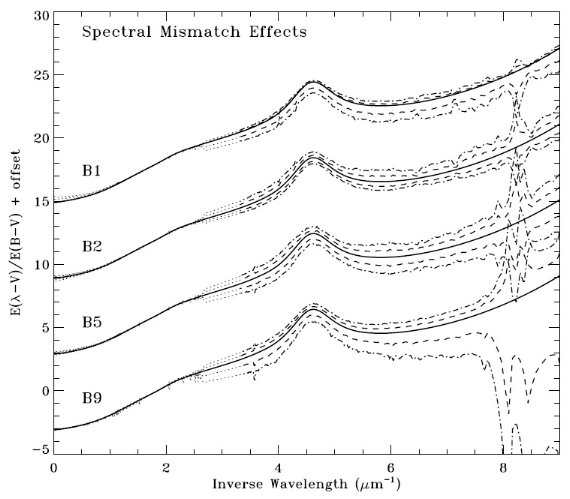
図１．ペア法でスペクトルに ±(1/2) のスペクトル型の間違いが生み 出す減光曲線の変化。実線＝正しい組み合わせ。間違いが ±(1/2) の 時、破線は E(B-V) = 0.30, 一点鎖線は E(B-V) = 0.15 で得た減光曲線。 UV 領域では分光測光観測から詳細な減光曲線が得られる。ミスマッチ線の 可視・赤外への延長は点線で示す。(1/λ) = 2.7 はバルマージャンプ、 (1/λ) = 8.2 は Lyα 線による。

　２．２．モデル大気法　

　３．標準星無しの減光決定　

　３．１．定式化　

　３．２．可変型減光曲線　

可変型減光曲線　 　図２に可変型減光曲線を示す。それは（１）．紫外減光(λ≤2700A) Fitzpatrick, Massa 1990 の表式を採用、と （２）．可視から赤外(λ>2700A) の錨点を３次スプライン内挿式 で表したものから成る。それらは IR(I1, I2, I3, I4), 可視 （O1, O2,O3), 紫外 (U1,U2）である。 内挿式を使用した理由はこの区間では信頼できる減光の表式が得られなかった からである。データが集積し、減光曲線の特徴間の相関が見つかれば 特性化が可能になるかも知れない。 　紫外部の表式　 　図２の点直線は Fitzpatrick, Massa 1990 の表式中の直線部を現し、 二つのパラメタ―を含む。 2175 コブはドルーデ型 D(x, xo, γ) プロファイルで表される。これは、コブ中心位置 xo, コブ幅 γ, コブ強度 c3 で指定される。最後に、遠紫外の立ち上がりは立ち上がり強度 c4 のみで指定される。その結果は、x = 1/&lambda: として、 　　k(λ-V) = c1 + c2x + c3 D(x,x0,γ) + c4F(x) 　可視ー近赤外　 　スプライン内挿の１０点は IUE スペクトル中 λ > 2700 A 部分 の分光測光値と可視、近赤外測光値に最少二乗フィットを行って決める。 U1,U2 は Fitzpatrick, Massa 1990 の UV 減光曲線 の λ = 2700, 2600 A での値なので固定されている。 O1, O2, O3, O4 は λ = 3300, 4000, 5530, 7000 A での測光値である。この区間には V バンドで k(λ-V)=0, B バンドで k(λ-V)=1 という制約が掛かる。近赤外 での I1, I2, I3, I4 は 1/λ = 0.25, 0.5, 0.75, 1.0 で、これら４点は次の式でフィットする。 　　In = k(λ-V) = kIRλn-1.84 - Rv

図２．可変型減光曲線。実線＝紫外減光(λ≤2700A) は３パラメタ― (Fitzpatrick, Massa 1990)で表現される。 破線＝可視から赤外 (λ>2700A) は錨点を３次スプライン内挿式で表す。それらは IR(I1, I2, I3, I4), 可視 （O1, O2, O3, O4), 紫外 (U1,U2）である。 このべき乗則指数 1.84 は Martin, Whittet 1990 から得たものである。この指数 自体はフリーパラメタ―として扱うべきであろう。将来の課題である。 　結局この区間ではフリーパラメタ―は可視域で２個、赤外で２個の計４個である。

　４．データ　

　５．初期成果　

　５．１．NGC 4665　

図３．散開星団 IC 4665 内の軽度に赤化を受けた B-型星９個の SED フィット。 黒丸＝ジョンソンUBVRI、黒三角＝ストレームグレン uvb、黒菱形＝ジュネーブ UB1B2VV1G 測光。赤外の白丸＝ジョンソン JHK、黒丸＝2MASS JHK.

図４．散開星団 IC 4665 のフィットから得られた減光曲線。星団星の赤化は E(B-V) = 0.14 - 0.25 に亘る。シンボルは図３に同じ。実線＝ベストフィット。 灰色帯＝モンテカルロ計算で決めた 1&igma; 不確定巾。一点鎖線＝平均減光 曲線 (Rv = 3.1)。2MASS と ジョンソン間の明らかなズレのため、近赤外減光は 標準曲線をそのまま使用した。一番上に９個の星団星の平均減光曲線を示す。 ＵＶでのエラーバーはサンプル標準偏差だが、これは個々の減光曲線に付いた 1σ エラーと同程度で、すなわち星団内の減光曲線は観測精度内で一様と 言える。

SED フィットの結果　 　図３に IC 4665 内の B-型星に対する SED フィットの結果を示す。 図４には我々の標準星無し法で求めた減光曲線を Hackwell et al 1991 がペア法で決めた減光曲線と較べた。フィットで決まったパラメタ―を表１，２ に示す。 　星団星減光曲線の比較　 　図５には今回得た減光曲線を Hackwell, Hecht, Tapia 1991 と較べた。 HHT 1991 の曲線のばらつきは当然きたされる程度である。驚くべきは標準星なし 法の結果の一致の良さである。この方法による減光曲線の散らばりは個々の減光 曲線の不確定性と同程度である。したがって、星同士の間の曲線の差はもしあった としても非常に小さいらしい。 　減光パラメタ―の散らばり　 　表３に IC 4665 の平均減光曲線パラメターとその散らばりを示す。第２列に パラメタ―の重み付き平均、第３列はそれらのサンプル偏差を載せた。第４列は モンテカルロ計算に基づいた個々の減光曲線パラメターに対する誤差を示した。 第３列の散らばりは個々のサンプルの誤差の二乗和から期待される値である。 これは、星団内の減光曲線に違いがあったとしても、我々の決定精度以下である ことを示す。

図５．散開星団 IC 4665 の減光曲線の比較。上：標準星なし法。下： ペア法(Hackwell, Hecht, Tapia 1991)。一点鎖線＝標準減光曲線。

　５．２．穏やかな赤化の星の減光　

図６．穏やかな赤化を受けた９つの B-型星のフィット。

図７．実線＝図６でフィットした穏やかな赤化星の減光曲線。点線＝ペア法で 決めた減光曲線。E(B-V) は 0.36 - 1.08 である。

　５．３．低減光の星　

Upper Scorpius Complex 　 　サンプル星は全て アッパーさそり座複合 (Garrison 1967) に属する、 中間-晩期 B-型星である。これ等の星は手法のテスト中に偶々巡り合った のであるが、この特別な領域の減光曲線は互いに似ているが、銀河系平均 曲線からは外れている。 　注意点１　 　注目したいのは、サンプル星のスペクトル型が B2.5 - B9 と広い範囲に亘って おり、減光曲線の特異星がサンプル星のスペクトル型によるものでないことを 示唆している。 図８．低赤化を受ける９個の B-型星のフィット。l = [347, 355], b = [18, 26]

注意点２　 　注意点の２はこの領域が ρ Oph 暗黒雲に近いことである。 ρ Oph = HD 147933 は図７に載っているが、この領域のすぐ南にある 星である。この星の減光曲線と領域星の平均減光曲線を図９の一番上で 比較した。面白いことに、紫外では似ているが赤外でずれる。領域星の 2MASS JHK データは Rv = 3.4 を示唆するが、HD 147933 は Rv = 4.3 となる。 図９．低赤化星の減光曲線。E(B-V) = [0.09, 0.22]. 一番上の平均減光曲線図 に点線＝ HD 147933 (l, b) = (353.7, 17.7) E(B-V) = 0.50 を比較のため示す。

　６．議論