Detemining the Physical Properties of the B Stars II. Calibration of Synthetic Photometry

　アブストラクト　

　１．イントロダクション　

　２．測光較正の概要　

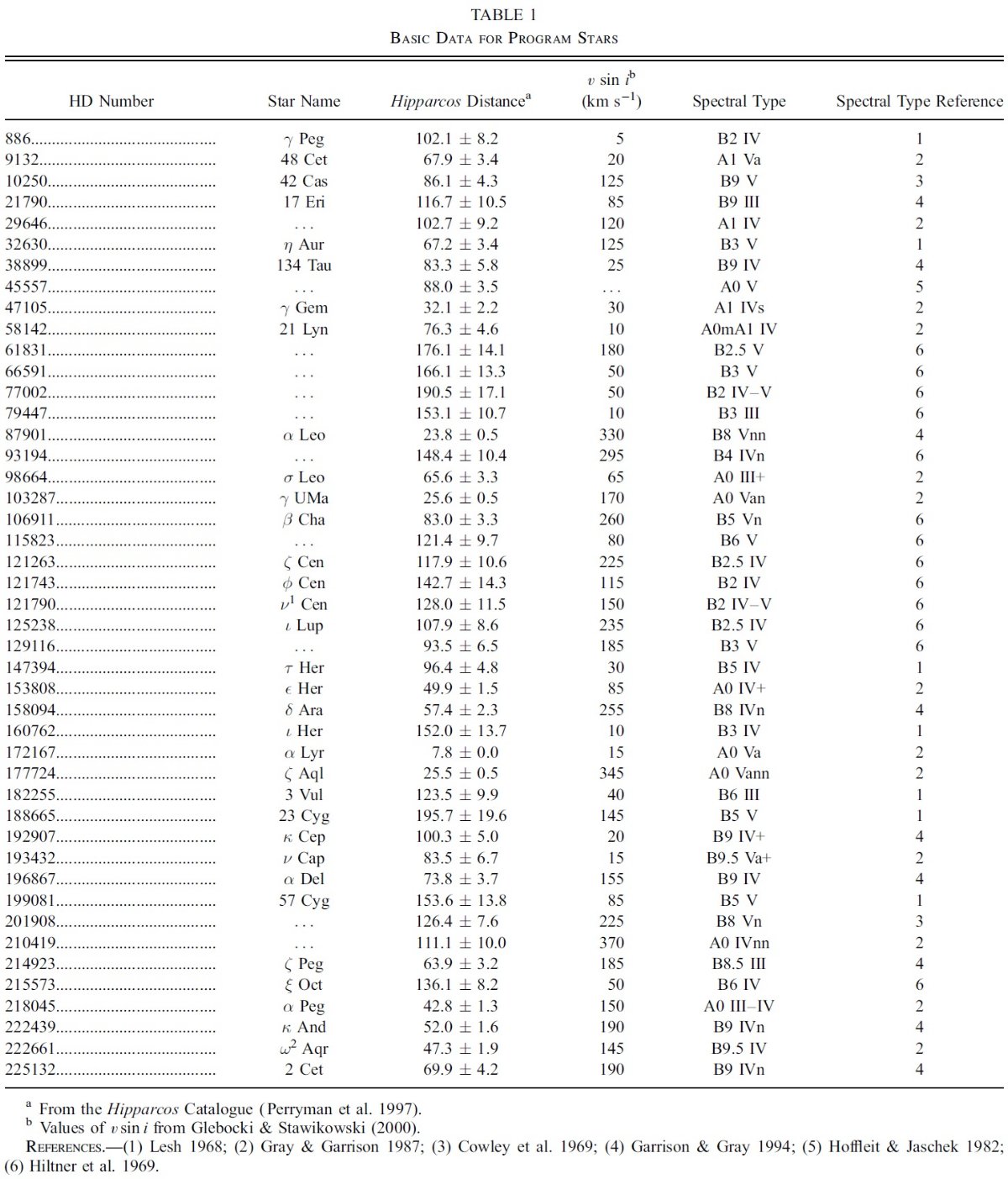
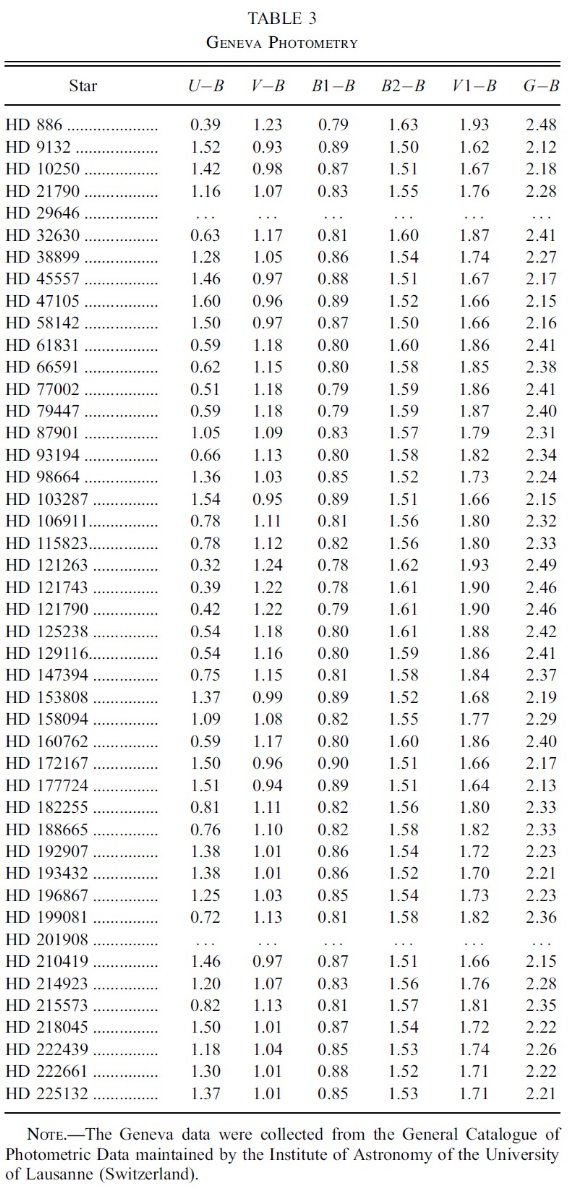
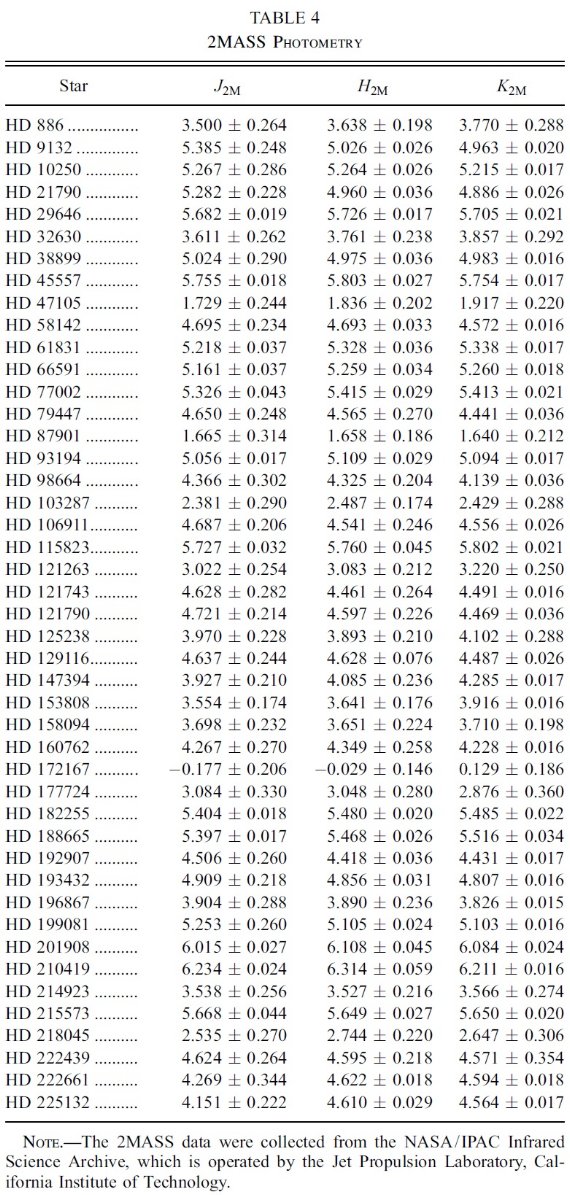
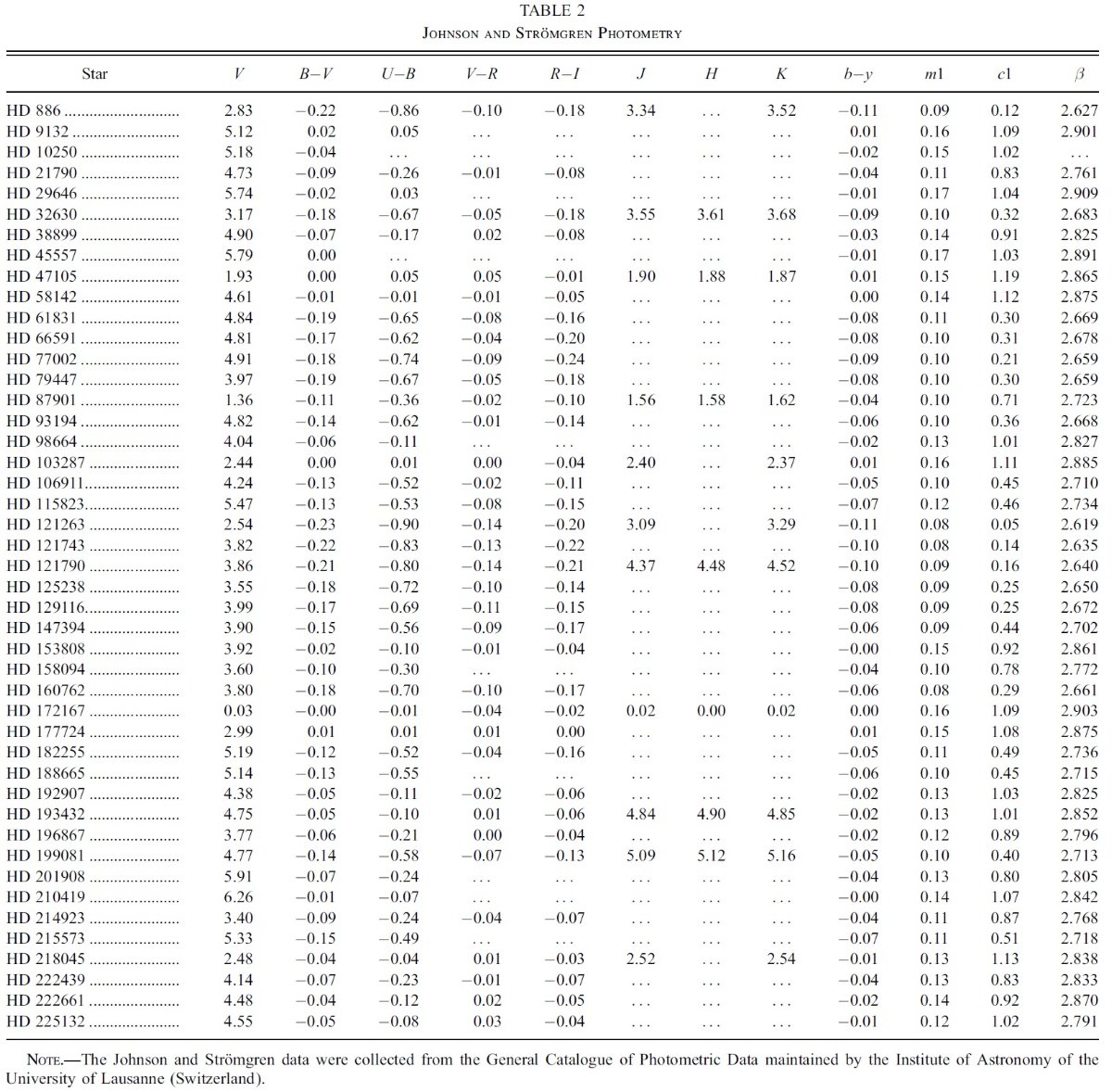
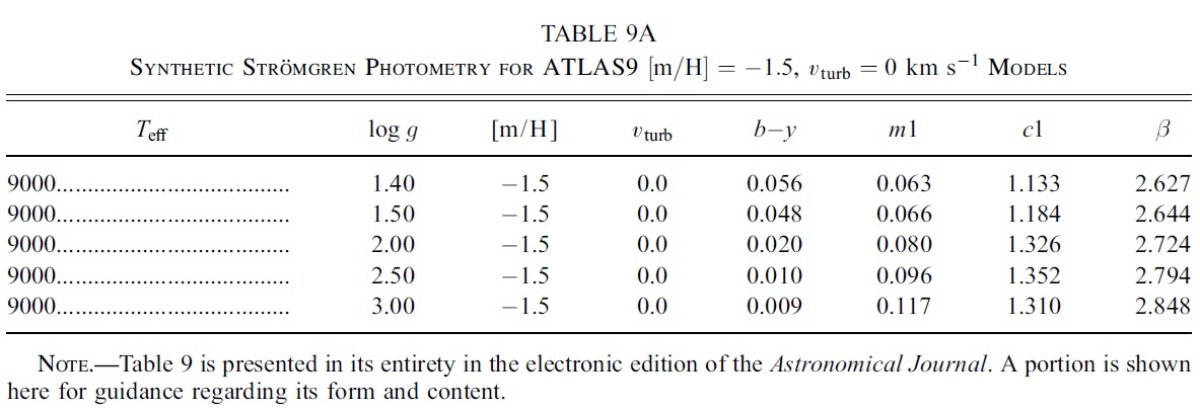
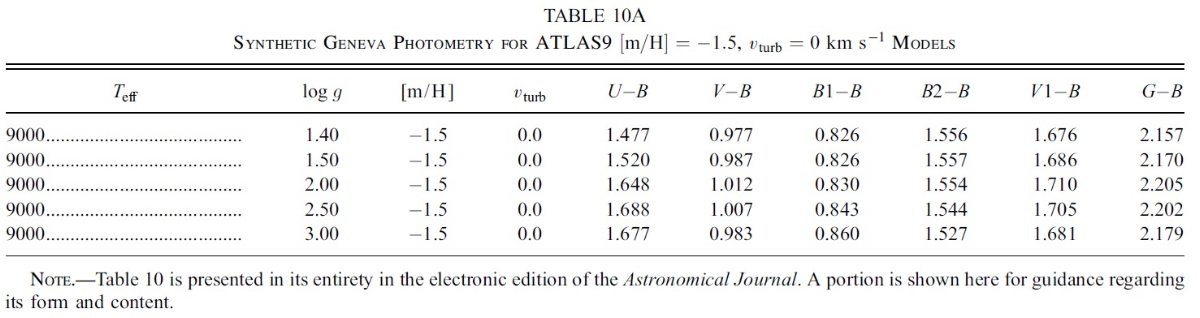
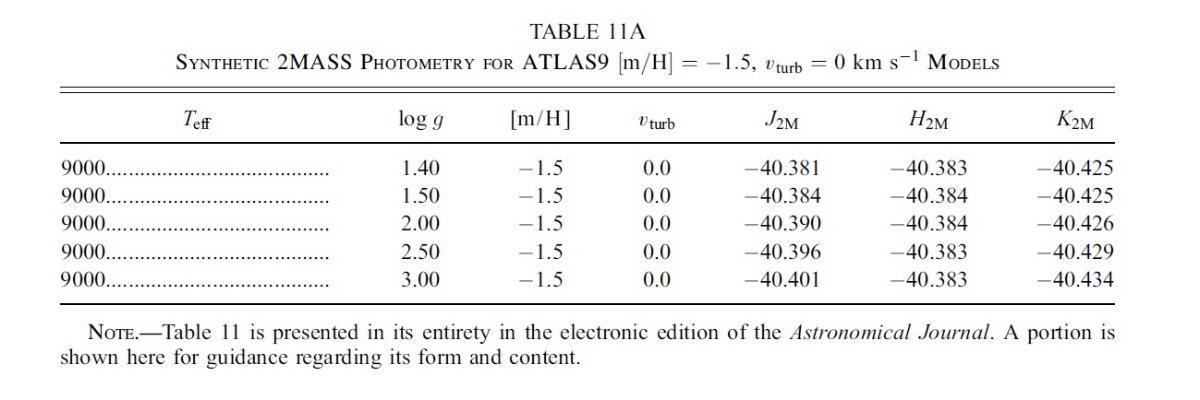
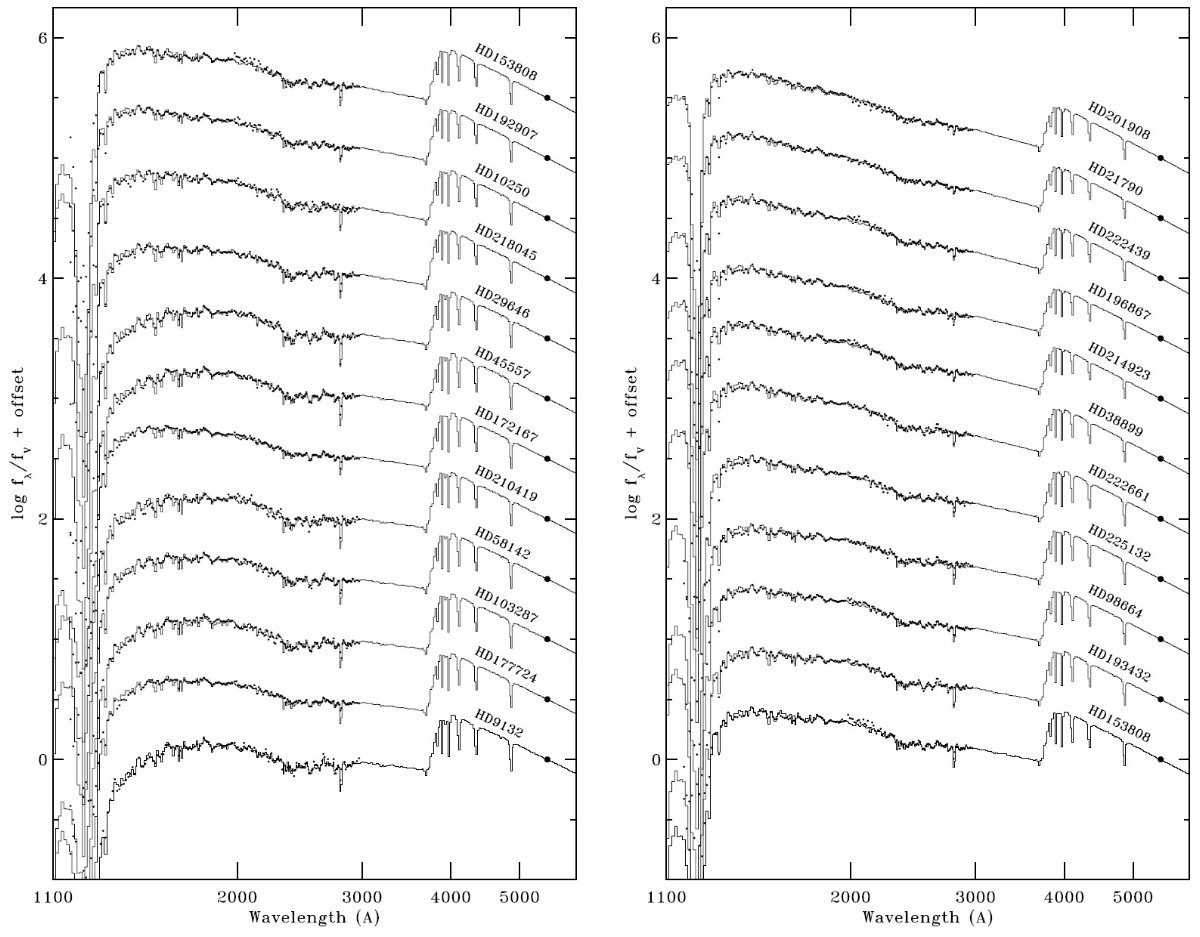
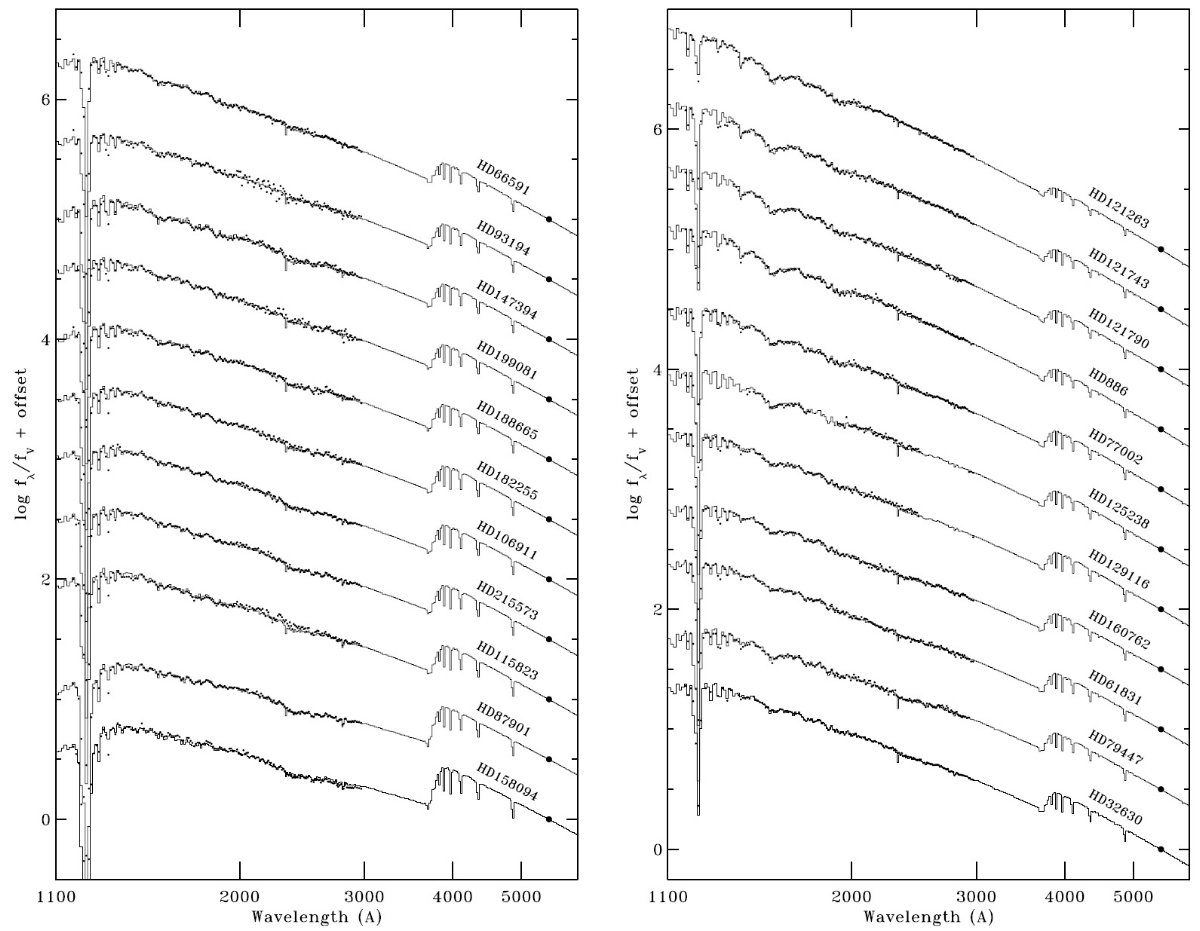
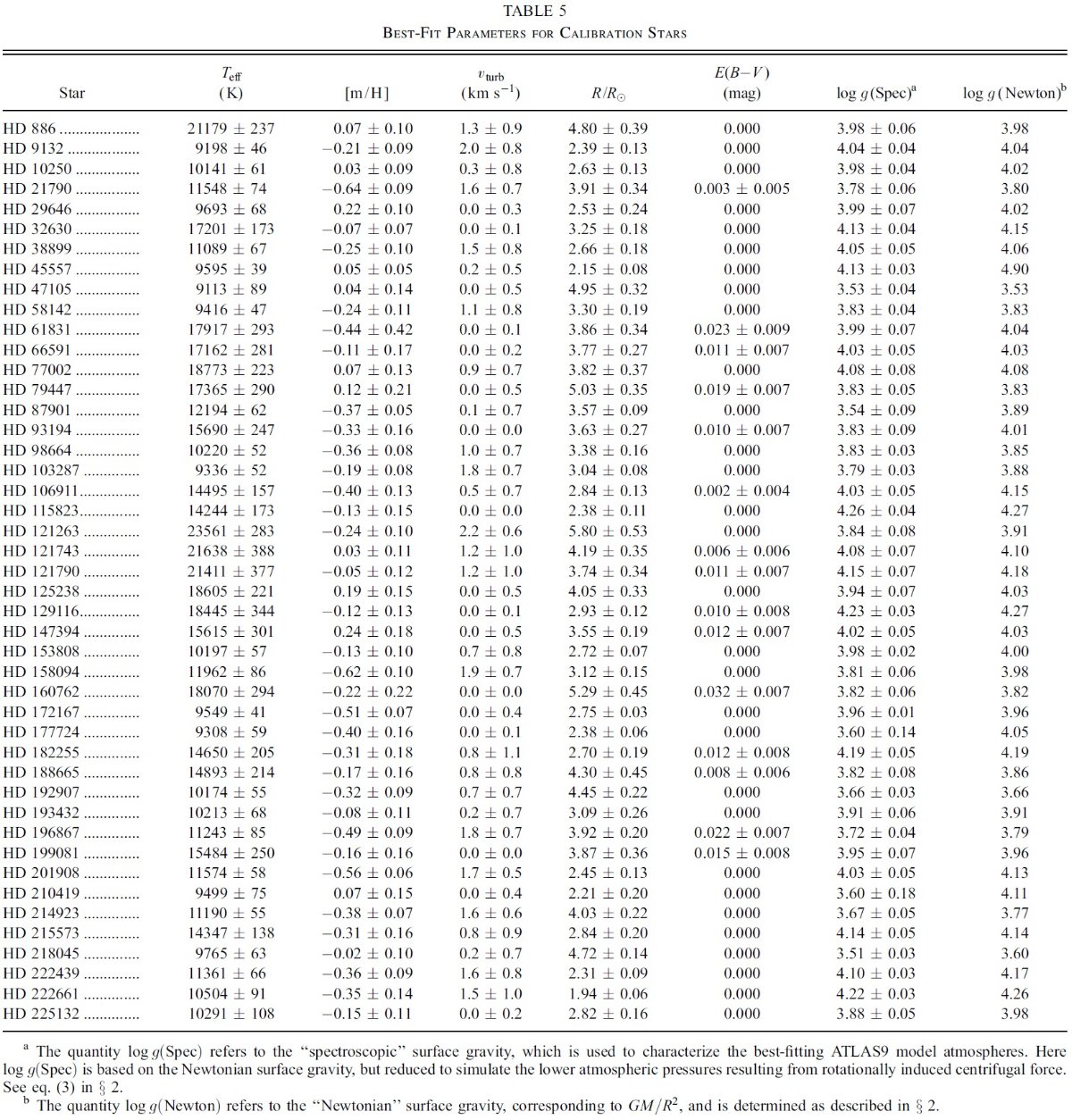
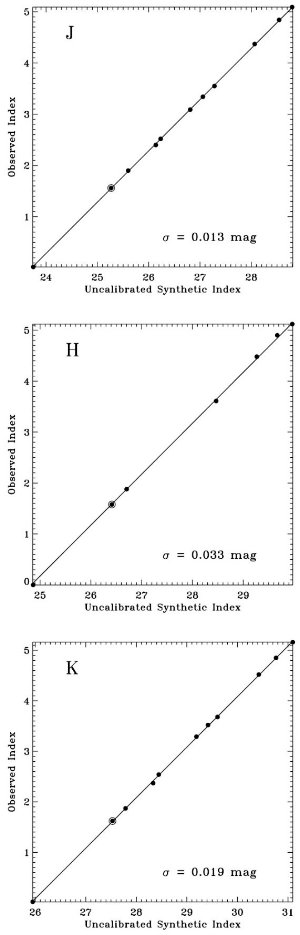
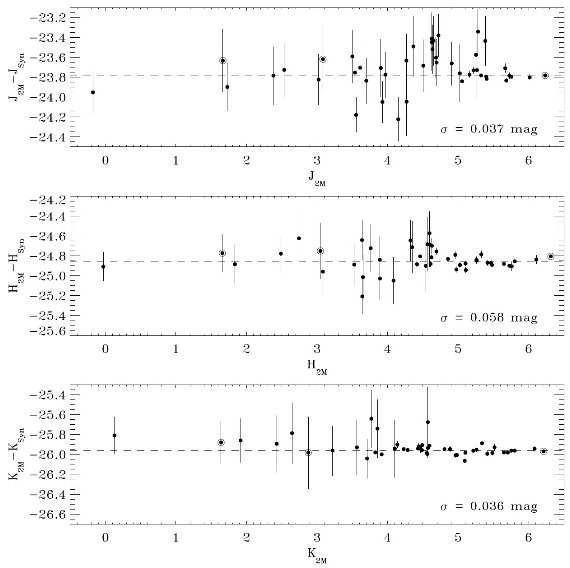
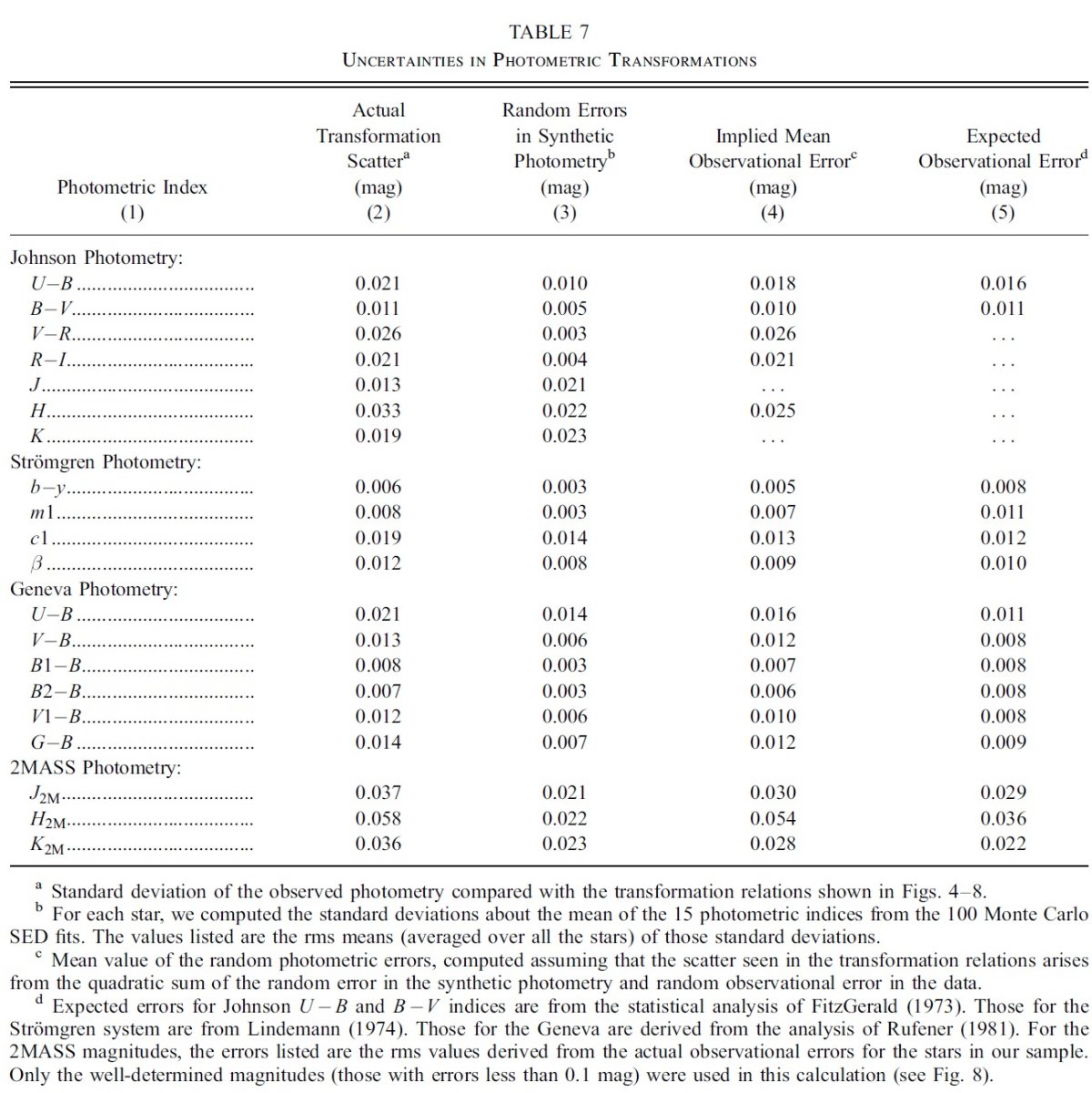
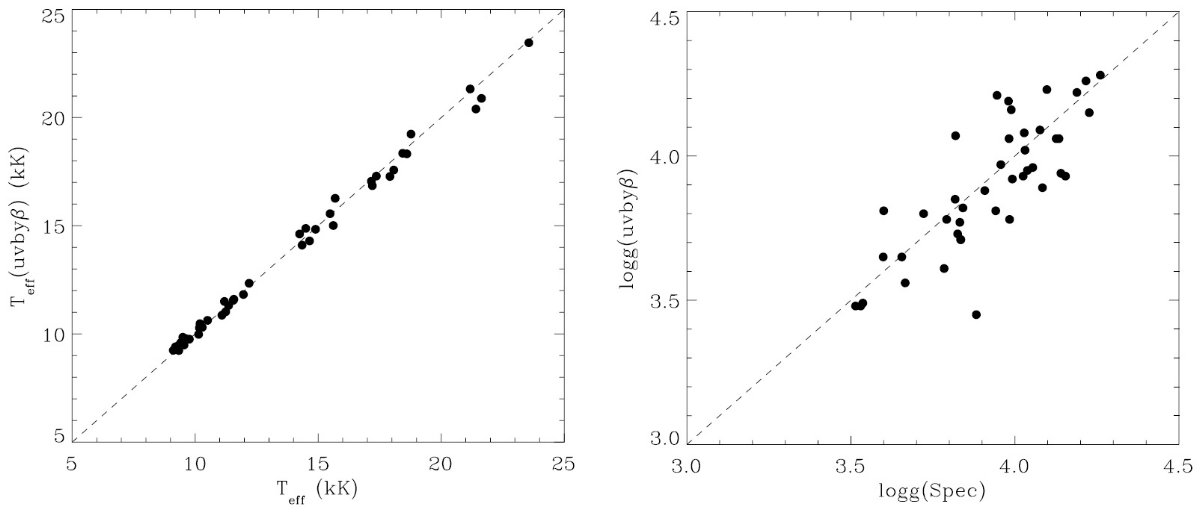
観測スペクトルのフィット　 　k(λ-V) = E(λ-V)/E(B-V) 　Rv = Av/E(B-V) 　A(λ)/E(B-V) = k(λ-V) + Rv 　Fλ = 表面フラックス、R = 星半径、d = 距離　として、 　fλ = Fλ(R/d)2 10-0.4E(B-V)[k(λ-V) + Rv]　　(1) 観測フラックス fλ は IUE (1165 - 3000 A) と V 等級である。 Fλ には ATLAS9 モデルを使用した。このモデルのパラメタ― は、Teff, log g, [m/H], vturb の４つである。減光はあったとしても 弱いので、とりあえず標準型 Fitzpatick 1999 の Rv = 3.1 を採用した。ここでの 減光則の違いは大きな影響は及ぼさない。これらの仮定に基づいて、fλ へのフィットから６つのパラメタ―、Teff, log g, [m/H], vturb, (R/d)2, E(B-V) を決めた。 　フィットからは log g がよく決まらない。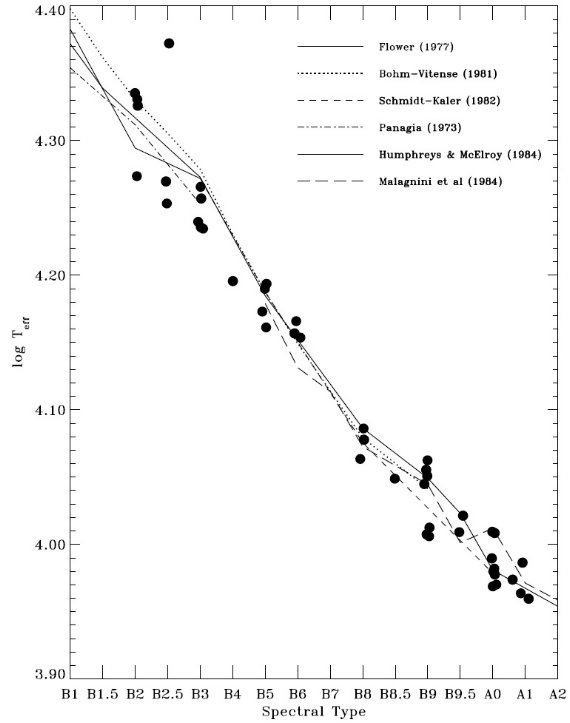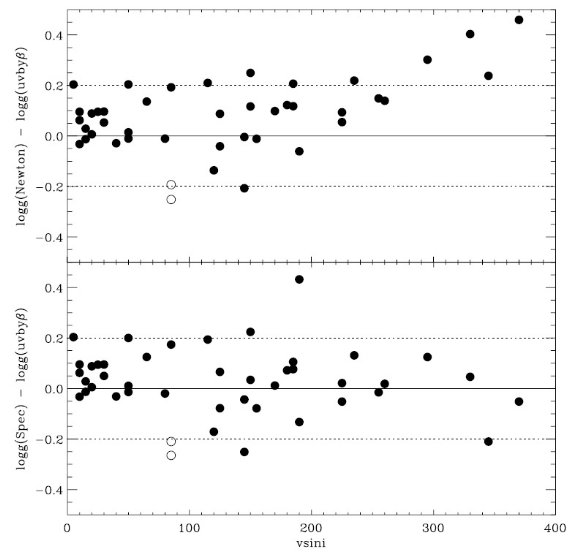　 　フィットの結果、 Teff, [m/H], vturb には強い制約が掛かった。 しかし、log g はよく決まらない。通常ならば、バルマー線のシュタルク効果 による線巾の拡大を調べると log g が決まる。しかし、そのようなデータが 得られていなかったので、その代りにヒッパルコスからの距離 d を用いる。 すると、式１へのフィットで R が決まる。主系列星の星構造モデルは、星の Teff と R が表面重力を一意に決めることを示している。これは図１に示されて いる通りである。こうして、d を用いることで、Teff, [m/H], vturb, R, E(B-V) の 5 パラメタ―で SED をフィットすることが可能である。それから、 log g = log g(Teff, R) の形で g を決める。 ただし、星の内部構造モデルで 決まる表面重力は "ニュートン" 重力 g(Newton) = GM/R2 である。 回転効果を近似的に組み込むため、"分光"重力 g(Spec) = g(Newton) - (v sin i) 2/R を考える。この補正重力を適切な ATALS9 モデルを選ぶために 使用する。 　結局　 　こうして、 UV スペクトル、V 等級、 v sin i, ｄ から５個のフィット パラメタ―と g(Spec) を決めた。

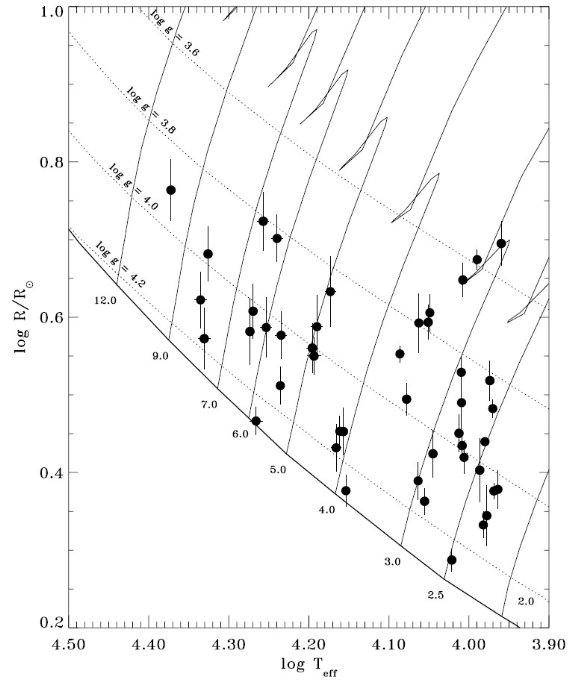
図１．Bressan et al 1993 モデル log R/Ro - log Teff 図。太い実線＝ ZAMS. 細い実線＝進化軌跡。点線＝ GM/R2 一定線。黒丸＝観測星。

　３．データ　

３．１．観測　 　観測星　 　観測星は正常で、非超巨星、非輝線星、低減光 E(B-V) ≤ 0.03、 の A, B 型星で IUE 低分散スペクトルとヒッパルコス視差 10 % 以下の 星が選ばれた。それらを表１に示す。 　測光データ　 　表２にはジョンソン UBVRIJHK とストレームグレン uvbyβ 測光を、 表３にはジュネーブカラー指数、表４に 2MASS 等級を載せた。 表３．ジュネーブ測光

３．２．モデル　 　モデルは Kurucz 1991 の ATLS9 モデル大気コードで計算した。 表４．2MASS 測光

　４．モデルフィッティング　

　４．１．不確定性　

　５．合成測光　

　５．１．計算　

表６＝フィルター感度曲線　 　モデル SED を得たので、次に合成等級を計算する。そのためのフィルター 感度曲線を表６に示す。非較正合成測光はモデル SED とフィルター感度曲線 の掛け合わせを積分して得られる。 　β 指数　 　β 指数は Hβ 線 4861 A を中央にした中間帯域 FWHM = 90 - 150 A 測光と狭帯域 FWHM = 15 - 35 A 測光の等級差である。様々な組み合わせで 実験した結果、標準システムに変換するとどの組み合わせも同じ値を出すことが 分かった。我々は、ガウシャン型で FWHM = 90, 15 A の組み合わせを使用した。 これは Crawford 1958 が使用したもので、変換が線形で使いやすい。 図３にその感度曲線を示す。 　SYNSPEC 　 　ATLAS9 SED は 20 A 巾で区切ったので β フィルターの合成測光は出来ない。 そこで、 Hubeny, Lanz 2000 の SYNSPEC プログラムを使って、 0.1 A 間隔の スペクトルを 400 A 区間で計算した。このスペクトルを用いて合成測光を行った。 表６．フィルター透過曲線のソース

図３．太い実線＝ 中帯域 β フィルター, FWHM = 90 A, の等価曲線。 一点鎖線＝　狭帯域 β フィルター, FWHM = 15 A, の等価曲線。 細い実線＝ B-型線、 Teff = 15,000 K, log g = 4, [m/H] = 0.0, vturb = 2 km/s, のモデルスペクトル。β 指数＝二つのフィルターでの等級間の差。

　４．２．較正　

図４．ジョンソンシステムの色指数間のフィルター較正関係。縦軸＝観測色指数。 横軸＝非較正の合成色指数。全枠について、実線は勾配１で平均差だけずらした 近似直線である。(B-V) に対してはこの近似で十分であるが、他の色指数は破線 で示した線形近似式が必要である。数式は略。二重丸の星は高速回転星。 図６．ジュネーブシステムの色指数。

図５．図４と同じプロットをストレームグレン色指数に対して行った。 m1 は勾配１だが、他の指数の勾配は１でない。 図７．ジョンソン J, H, K システムの色指数。

合成測光と観測の比較　 　合成測光の最終段階は合成等級及び色指数と観測等級及び色指数との関係 を決定することである。図４−図７はそれをジョンソン、ストレームグレン、 ジュネーブシステムで行った結果である。図８には 2MASS 等級の比較を行った。 　全体として　 　図４−８までの結果から、 ATLAS9 モデルによる合成測光の振る舞いは 正常で、標準測光系に容易に変換できることが判った。

図８．2MASS システムの観測と非較正合成測光との関係。

　６．最終結果　

　７．議論　

７．１．以前の結果との比較　 　Teff とスペクトル型の比較　 　図９には Teff とスペクトル型の関係を示す。ζ Cen(HD121263) = B2.5IV のみが他から外れている。しかし、ＵＶスペクトルは B1V 星 HD31726 と似て おり、逆に他の B2V 星と異なるので、分類が悪いのかも知れない。図９には 他の研究結果も載せたが、我々の結果はそれらと一致する。 　ストレームグレン測光との比較　 　A-型と B-型星の Teff と log g を導く通常の方法は、ストレームグレン uvby 測光である。しかし、測光から [m/H] と vturb を B-型星に 対して求めるのは難しい。我々は Napiwotzki の uvby 法に従って、 Teff と log g を求め、それを我々の方法で求めた値と図１０で比較した。 極めて良い一致が得られた。図１０の Teff と log g を決める二つの方法で 入力されたデータは完全に独立であることを強調したい。ただ、どちらも ATLAS9 を基礎においているが。 図９．丸＝観測星。折れ線＝様々な研究による Teff とスペクトル型の関係。 見易さのため、小さなランダム横ずれを加えた。

[m/H] 　 　 Fitzpatrick, Massa (1999) が指摘したように、UV 連続光から導くメタル量 は主に鉄グループの元素量である。Smith, Dworetsky 1993 の高分散 IUE スペクトルの解析結果と較べると、最大、最小メタル量も一致していて 有望である。 ( でも値は違っているんじゃないかな？) 　vturb　 　Smith, Dworetsky 1993 は vturb の測定結果も示している。しかし 彼らの結果と我々の結果に相関はなかった。我々の得た結果が誤差を僅かに上回る レベルなのでこの結果は当然でもある。 　視角　 　Hanbury Brown et al 1974 は我々の星の内、γ Gem, α Leo, α Lyr の３つの視直径を 1.39, 1.37, 3.24 mas と定めた。表５の値 から我々の得た視直径は 1.43, 1.39, 3.28 mas である。 　７．２．エラー　 図１１．log g 決定の系統的効果。上図：[log g(Newton) - log g(ubvy)] と v sin i との関係。下図：g(Newton を g(Spec) に変えると系統誤差が消える。

　８．まとめ