
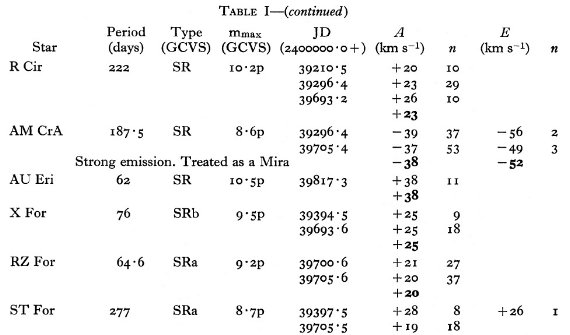
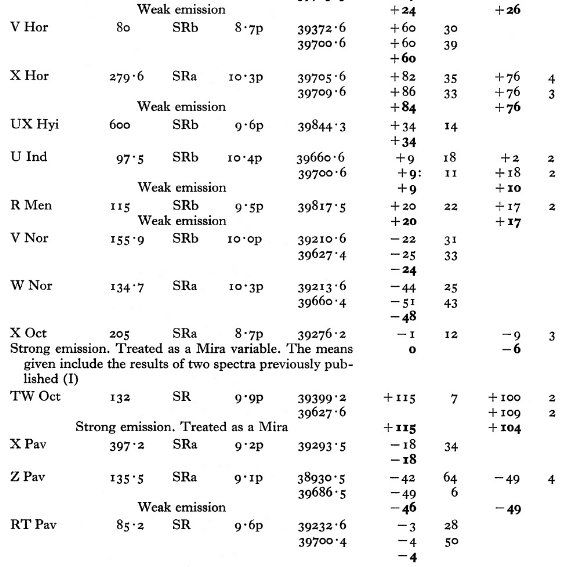

| Kottamia Obs で撮った北天の 67 M-型 SRs と Radcliffe Obs での南天 53 M-型 SRs の視線速度を得た。それに既存データを加えて SRs の運動を調べた。 運動の平均が周期により変化する証拠はなかった。ただし P = 60 - 140 d の 範囲で弱い輝線を示す星は他より速度分散が大きい。ただこれは高速のサンプル を加えるか外すかで結果が変わる。 |
203 個のデータから得た平均は、 u = -20±4, v = -27±4, w = -12±5 α = 42±6, β = 42±6, γ = 34±9 セミレギュラーは古い円盤種族に属する。セミレギュラーに対して若い天体の 銀河系が外向きに膨張する証拠はない。密度勾配は
|
|
赤い変光星 赤い変光星は非均質なグループでそれを均質な副グループに分割する上で、 運動学的性質は重要である。最近の努力はミラ型星の視線速度に向けられてきた。 セミレギュラーの観測数は少ない。そこで、セミレギュラーの視線速度を観測 してミラとの関連を調べた。 |
セミレギュラー サンプル星の大半は GCVS で SRa, SRb あるいは単に SR と分類されている。 セミレギュラーは平均振幅が 1.4 mag 以下である。 |
|
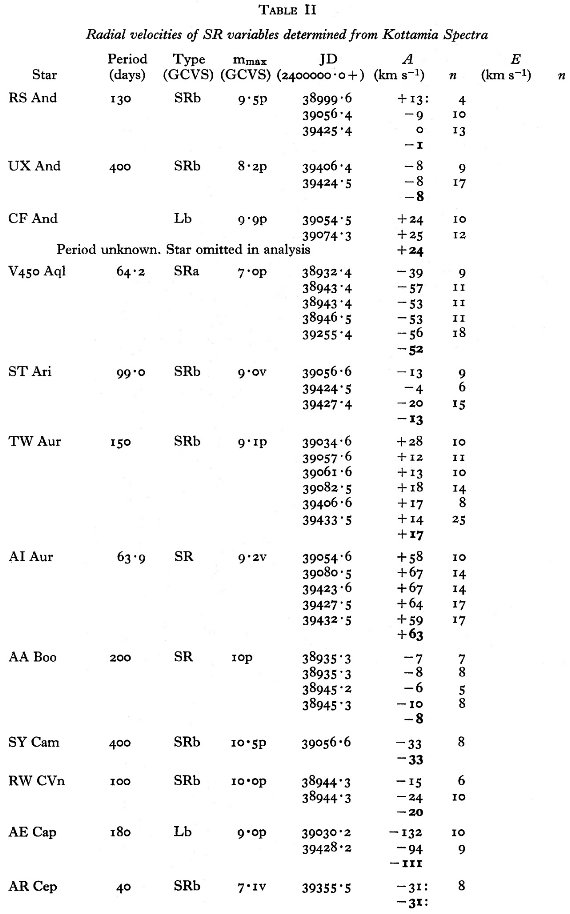
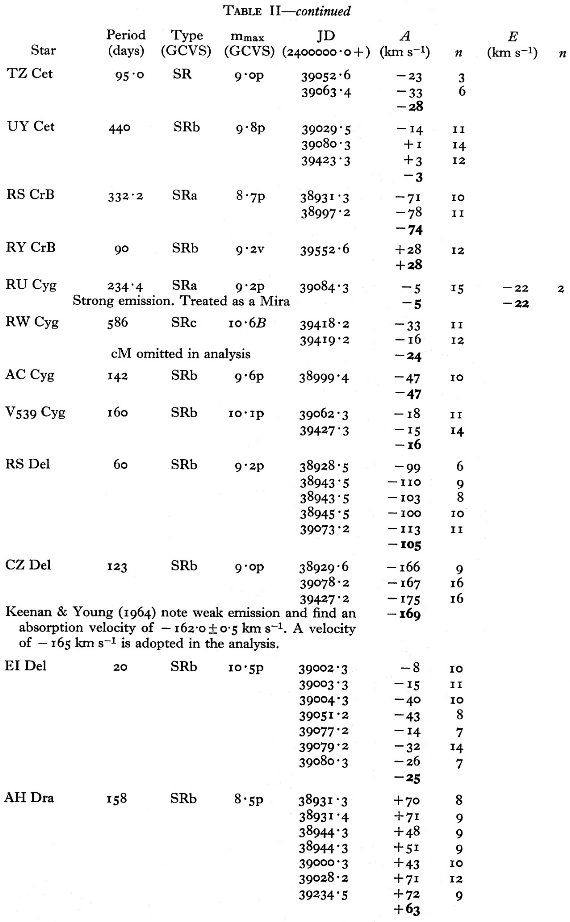
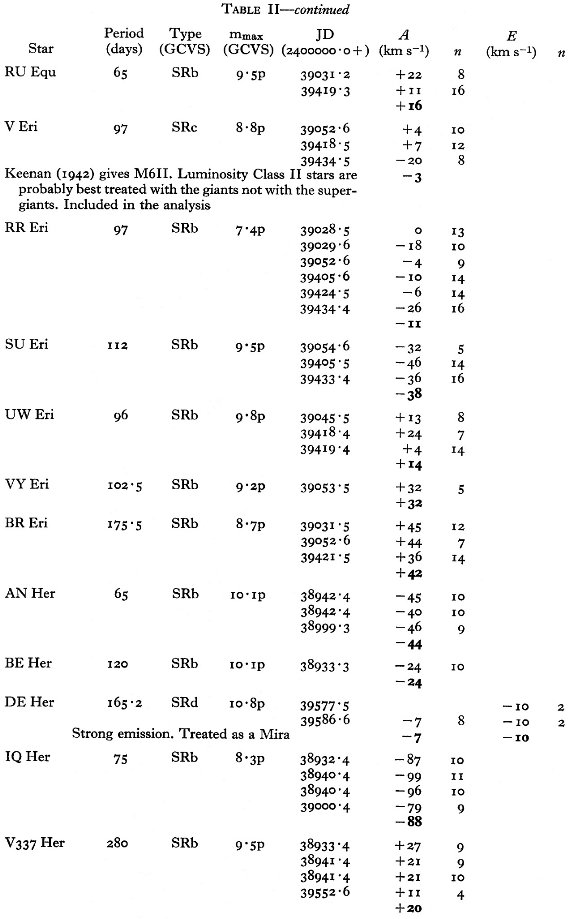
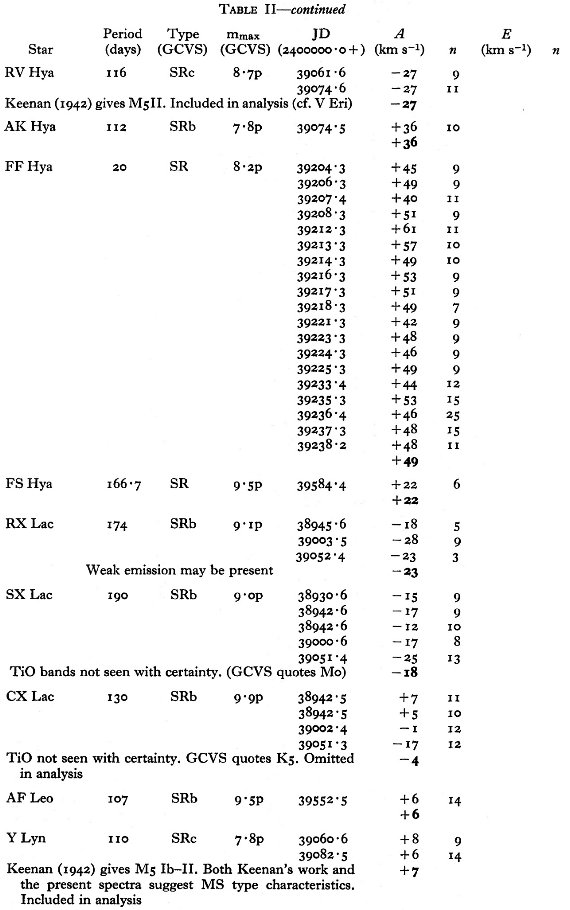
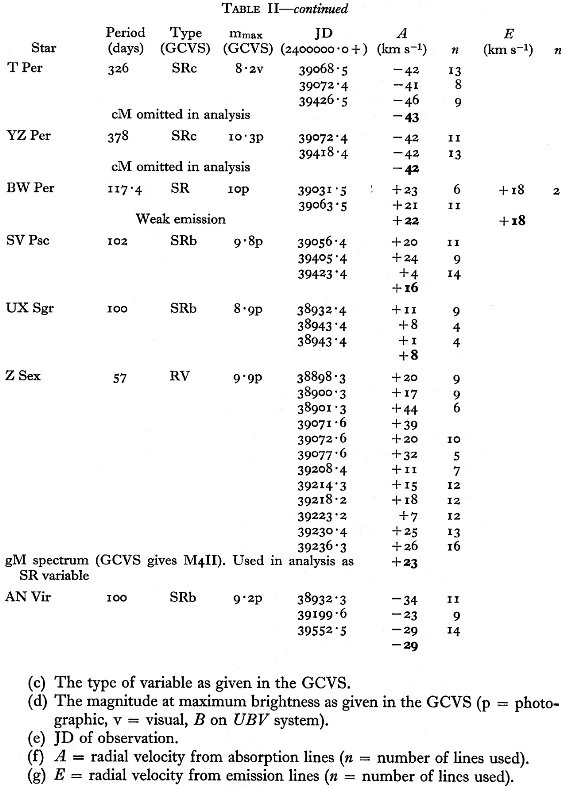
エラー 表1にはラドルクリフ乾板から得た、53 星の 91 速度を示す。同じ星の観測 値から得た平均エラーは 2.6 km/s である。 表2にはコタミア乾板から得た、67 星の 207 速度を示す。平均エラーは 4.9 km/s. |
"CM", "Me" 星 超巨星 SR はこの観測には含まれない。表1、2のノートに "cM" と書かれて いるのがそれである。光度クラス II は巨星と看做す。それらは GCVS では SRc に分類されることがある。輝線がミラ型星と同じくらい強い星は表のノートに "strong emission" と記され、ミラ型星として扱われる。 |
  |
  |
   |
   |
|
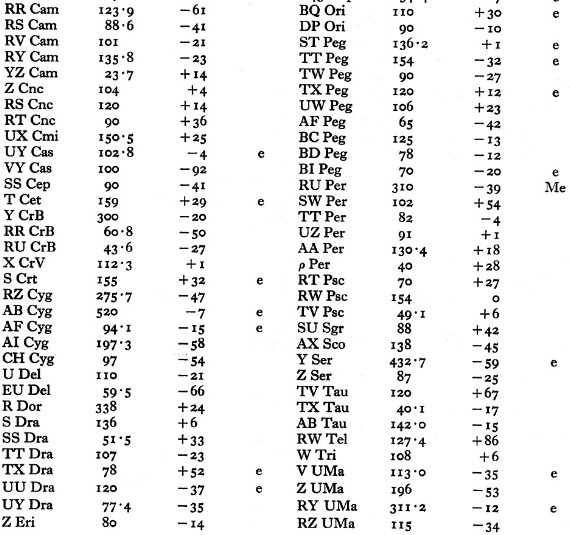
表3にはこの解析に利用した過去のデータをまとめた。視線速度データは
主に Joy 1942 のものである。"Me" はミラとして扱う星、"e" は弱い輝線が
あることを表す。超巨星はこの表には含めない。
表3.過去に視線速度観測がある星のリスト 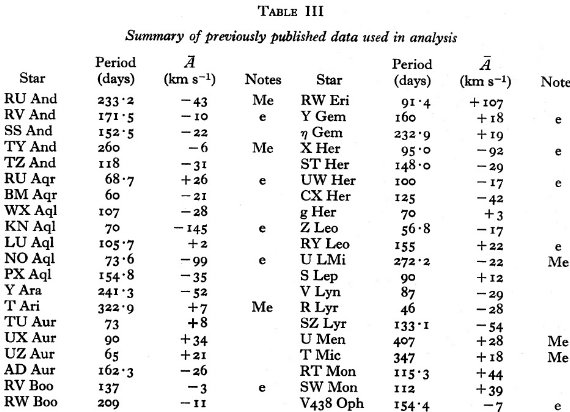 |
  |
|
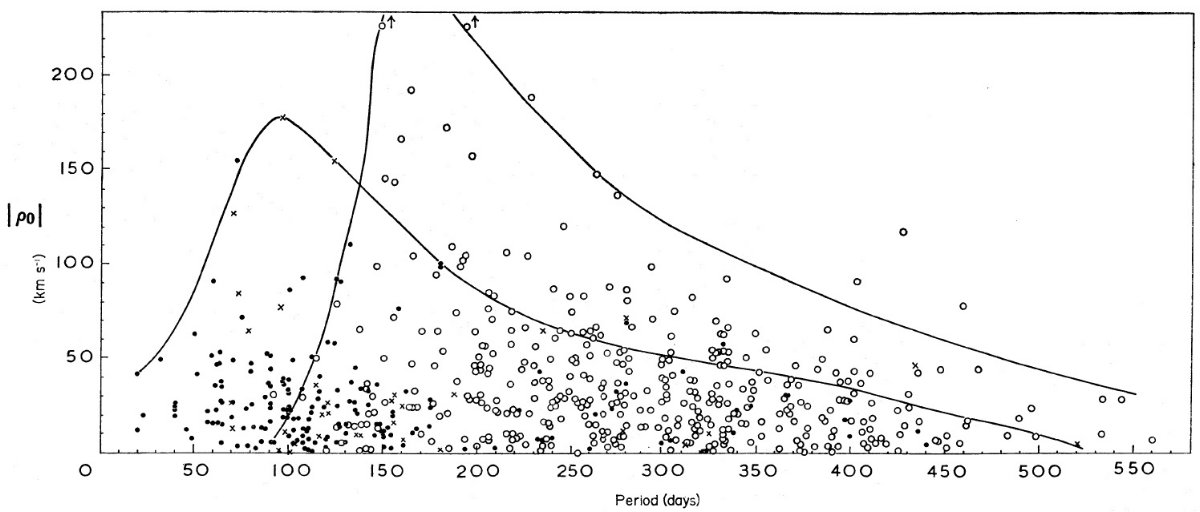
3つのグループ ここでは、ミラ (Me) 型星に対する Feast (1963) の表2の結果とつなげてセミレギュラーの運動を調べる。遠方のミラに対する、 Smak, Preston (165), Feast (1966) のデータは使わない。我々は星を3つのグループに分けた。それらは ミラ (Me), 弱い輝線を示すセミレギュラー, 輝線のないセミレギュラーである。 それらは続いて周期で副グループに分けられる。 図1=残差運動と周期 図1には残差速度 ρo =局所太陽運動を差し引いた後の視線 速度、を周期に対してプロットした。ρo は次式で定義される。 ρo = A +uo cos l cos b + vo sin l cos b + wo sin b ここに A = 星の平均吸収速度、uo, vo, wo は太陽運動で、それぞれ銀河中心からの動径方向、銀河系回転方向、北銀極方向の速度 成分である。採用した値は、 uo = 10.1 km/s, vo = 13.0 km/s, wo = 6.25 km/s である。 周期分布外郭線 図1の (a)=ミラ型星の分布外郭線、(b)=セミレギュラー全体の分布外郭線。 ミラ型星の ρo 分布に関しては、 Feast (1963) に述べた。セミレギュラーの ρo 分布の形もミラと似るか、 最高点が短周期側に移っている。ただ、最高点位置は 60 - 140 d にある 4 つ の高 ρo 星の扱いで大きく変わる。 |
周期サブグループ 3つのグループの夫々を周期で12のサブグループに分けた。それを表4に 示す。弱い輝線のあるセミレギュラーは P = 60 - 140 d サブグループにのみ 十分な数のサンプルがあるので独立のサブグループとした。その他は輝線無し セミレギュラーに混ぜた。 サブグループの平均運動 各サブグループ毎に次の式を最小二乗で解いた。 A = u cos l cos b + v sin l cos b + w sin b + K その解き方は次の3種で行った。 (i) u, v, w, K を求める。(ii) K = 0 として解く。 (iii) u = -uo = -10.1 km/s, v = -vo = -13.0 km/s, w = -wo = -6.25 km/s, K = 0 を仮定して V を決める。 それぞれの結果は表4に示す。 解 (ii) を使用 解 (ii) に対する残差速度 ρ を速度散布度 = dispersion α, β, γ 決定に用いられた。 ρ2 = α2(cos l cos b)2 + β2()sin i cos b)2 + γ2(sin b)2 |
 |
 |
 |
 |
4.1.K 項サブグループ 1 - 5 の平均 K 項 = -4±3、 サブグループ 6 - 12 の平均 K 項 = 0±2 なので K 項はないと考えてよい。4.2.v 成分と μv 成分平均値平均運動の v 成分と、残差速度の r.m.s. μ が周期 P でどう変化するかは Feast (1963) で論じた。新しいデータでの結果を図2と図3に示す。図にはセミレギュラーに 対する結果も示す。図2からはセミレギュラーの周期が速度成分 v に関係す る証拠はない。 残差速度 r.m.s. μ 図3からはセミレギュラーの周期が μ にも関係しないよう に思えるが、グループ2=弱い輝線を示す周期 6- - 140 日のセミレギュラー の μ だけは他のグループよりかなり大きい。ただし、この結果も数個の高 速度星を統計に含めるかどうかで大きく変わる。表4には AM Sgr を除いた グループ2a と AM Sgr と CZ Del を除いたグループ2b に対する μ を 示した。図3を見ると、それでもなおグループ2の μ は大きいようである が、更なる観測が必要である。u と w 成分も周期依存は認められない。 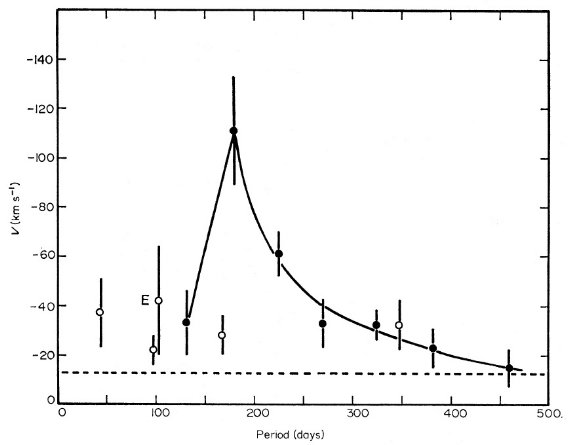 図2.平均速度の v 成分 (表4の解 iii) と周期の関係。 黒丸=ミラ。白丸=セミレギュラー。グループ2=輝線付き、周期 60 - 140 d のセミレギュラーは "E" と記す。破線= v=-13 km/s ラインで若い天体に相当。 |
4.3.平均速度全 SRs の平均運動と残差速度の散布度もしかしたらグループ2は外れるかも知れないが、セミレギュラーは全て 同じ運動種族に属する。それでグループ 1 - 5 の 203 SRs の平均運動と散布度 を求めた。 u = -20±4 km/s, v = -27±4 km/s, w = -12±5 km/s α = 42±6 km/s, β = 42±6 km/s, γ = 34±9 km/s この値はグループ2を除いてもほとんど変わらない。 古い円盤種族? 上の v = -27 km/s は若い天体 (Feast, Shuttleworth 1965) の v = -13 km/s と比較した時、明確なストロームベルグ非対称回転を示す。この非対称回転運動 の存在は図2で破線= -13 km/s との比較で明らかである。このズレは惑星状 星雲 (Minkowski 1964, Oort 1965) と P = 330 d 付近のミラ型星 (Feast 1963, 及びこの論文の図2)とよく似ている。セミレギュラーの速度散布度も同様 に惑星状星雲と周期 330 d ミラに似る。この運動特性は通常 "古い円盤種族" に付与されている。w = -12 km/s は標準値 -wo = -6 km/s とあまり 変わらない。 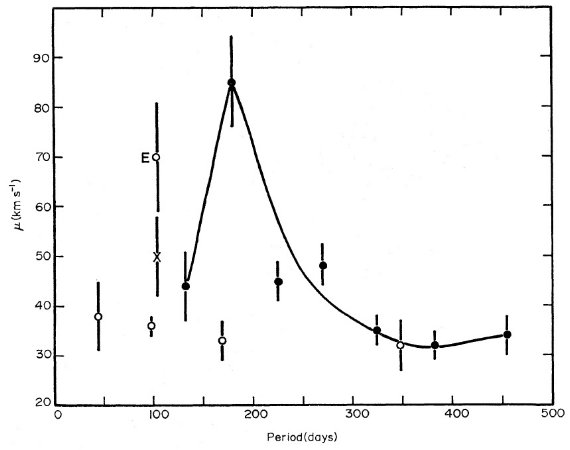 図3.μ = 残差視線速度の r.m.s. (表4の解 iii) と周期の関係。 黒丸=ミラ。白丸=セミレギュラー。グループ2=輝線付き、周期 60 - 140 d のセミレギュラーは "E" と記す。バツ=それに外していた高速度星2個を加えた 点。 |
|
Kerr モデルは間違い 太陽運動の u 成分、銀河中心方向からの運動成分、は太陽付近の若い星とガス が 7 km/s で膨張している可能性との関連で興味深い。これは Kerr 1962 の 有名な 21 cm 観測結果の解釈である。これが正しければ古い種族天体は若い 天体に対して内向きの速度を示すであろう。Feast 1964 は若い天体やガスに 対して Me 変光星が僅かに外向きの運動を示すと述べた。今回の解では Me 変光星は Δu = +3.5±3.3 km/s, つまり Δu は正で、 若い天体の u = 10.1 km/s よりさらに外向きの速度を持つ。この値自体は ゼロとあまり変わらないが、Kerr のモデルからは Δu = -7 km/s が期待 されるので、それとは有意に違うと言える。 高速度星 Blaauw 1970 はあるグループの星は高速度星の混入による影響を受けるかも 知れないと指摘した。 彼は P = 150 - 200 日の Me 星の空間速度は特にその 影響を受けているのではないかと述べた。表5では Me と SR の Δu ( 解 ii) は色々なグループ分けが出来る。疑いなく、高速度星の u 成分の非対 称性がグループ2(輝線ありの P = 6- - 140 d SRs)とグループ7( P = 145 - 200 d の Me)に影響している。双方共に高速度星を含んでいる。しかし、少数 の高速度星では全体の平均速度を大きく変えることはできない。我々の結果は 太陽近傍で古い円盤種族星が若い天体に対して外向きの運動をしていることを 示す。しかし、不定性は大きく Δu = 0 の可能性もある。 |
 表5.若い天体 (u = -10 km/s) と較べた Δu |
|
γ/α セミレギュラーの速度散布度の比は、 β/α = 1.0±0.2, γ/α = 0.8±0.2 Feast (1963) によるミラの値は、 β/α = 0.87±0.11, γ/α = 0.77±0.14 であった。これは若い天体に通常適用される値 0.5 と較べると大きい。特に興味深いのは γ/α が 1 に近いことである。この比は第3積分が存在しない限り、 定常状態では 1 になる。この問題の解決はさらに進める必要がある。 密度勾配 Feast (1963) と Oort 1965 は速度分布と密度勾配の間に次のような関係を導いた。
ここに、銀河回転速度 = θc = 250 km/s、非対称速度 θc - θm = 12 km/s = SRs の v = -27 km/s と 太陽運動の vo = 15 km/s の和。 |
SRs に対して数値を入れると、
Oort 1965 の表5から、 SRs と同じくらいの非対称運動を示す天体、惑星 状星雲と P > 300 d の Me 変光星を見ると、密度勾配は -4.2±1.8 と -3.3±1.5 を示す。これら3つを平均して古い円盤種族の密度勾配として、
を得る。 将来の課題 古い円盤種族の密度勾配を直接決定することは現在非常に不正確な問題である。 この正確な値を運動学的に決まる値と比較することは速度楕円体理論の重要な テストである。 |
|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
