The Kinematics of Me Variables towards the Galactic Centre and a Comparison with the Planetary Nebulae

　アブストラクト　

　１．イントロダクション　

前論文のまとめ　 　 Feast (1963) では、おもに Feast と Merrill による Me 変光星の視線速度を解析した。 それらの運動学的特徴と、さらに運動と周期との関係が明らかになった。 太陽近傍のみならず、微分回転が検出できるほどには遠方のデータも解析さ れた。しかし、遠方星の数は多くなく、21/373 が 2 kpc より遠方であるに 過ぎない。この論文では Me 星が銀河系全体の構造と運動を明らかにするのに 有用であることを示す。それが可能なのは次の二つの理由による。 　(a) 周期による分類　 　周期によるグループ分けは年齢分けと看做して良い。 　(b) 遠方星の観測が可能　 　現存望遠鏡でも遠方の Me 変光星の視線速度を観測可能である。特に輝線の 観測は吸収線に較べずっと短時間で済む。 　ライデンサーベイ　 　銀河中心方向の星の運動に関しては殆ど知られていない。この方向での Me 変光星の観測プログラムは 1958 に開始された。そこで役に立ったのはヨハネ スブルグ・ライデン観測所での変光星サーベイである。多数の暗い変光星が このサーベイで発見され、ファインディングチャートが作られた。 この論文のサンプルはそこから選ばれた。 　輝線測定　 　視線速度の測定には全て輝線、おもにバルマー輝線、が用いられた。

図１．今回視線速度を観測した長周期変光星の天空上位置。黒丸＝ Me, 白丸＝ Se.

　表１．長周期変光星の視線速度　

　２．輝線速度から吸収線速度へ　

A - E　 　以前の研究で星本体の視線速度 E は変光極大付近の吸収線速度 A でよく 表されることが判っている。この差 A - E は変光位相により変わる。 A-E と周期との関係は、 　 Feast (1963) で調べられ、この論文でも用いられた。 　複数回観測　 　19 星では観測が２度行われ、速度差の散布度は 12 km/s であった。 　表２．吸収線の推定視線速度

　３．絶対等級　

表３．周期 149 日以下の変光星 　短周期星の分裂　 　長周期 Me 変光星の絶対等級に関しては比較的よく分かっているが、短周期 の場合は面倒である。周期 150 日以下、変光巾大、晩期又は中間スペクトル型、 で強いバルマー輝線を示す星は絶対等級の異なる二種の星種族の一方に属する 可能性が強い。 　(a) SRd 型　= 基本振動　 　Feast 1965 では SRd を短周期 Me ミラと直接つながっているとした。彼は それらを基本振動する星の系列と考えている。この解釈はそれらの運動特性、 絶対等級、極大時スペクトル型が M-型より早期であること、さらに少なくとも 幾つかののケースで低メタル星を想起させる特異性などに基づいている。 これ等の星は球状星団と似た種族を構成しているようだ。 　(b) 短周期 Me 変光星 = 第１倍音　 　 SRd と同じ周期区間に属するが TiO が強い。運動特性と絶対等級からそれら は第１倍音振動星で、その基本振動周期は 330 日付近にあると考えられる。 これらの星は SRd より 1.5 mag 暗い。 ("明るい" じゃないのか？) 　表３＝短周期変光の５星　 　表２にある周期 149 日以下の変光星 5 個を表３に再録した。初めの４つは TiO は完全にないか、極めて弱い。これらは SRd であろう。最後の V947 Sgr は強い TiO を示す。他の特徴からもこの星はグループ(b) の短周期ミラ であろう。 　基本振動星と倍音振動の対応　 　もし、短周期変光星が第１倍音で振動しているなら、その基本振動は 330 日 付近に来る。周期 330 - 350 日の変光星は太陽系周辺の Me の中では最も頻度 の高いグループを成すが、今回の銀河系中心方向サンプルでは極めて少ない ことが図２の黒点分布から明らかである。従って、第１倍音星も極めて少ないと 考えられる。参照のために太陽近傍での周期分布を図２にヒストクラムとして 示す。

図２．見かけ等級 SPg と周期 の関係。バツ＝ Se. 白丸＝ V947 Sgr. その 基本振動周期は 348 日である。 RV Sgr (SPg = 7.13, P = 318 d) は枠外。 ヒストグラムは Feast 1963 の視線速度既知の太陽近傍見かけ等級限界での Me 星の周期分布、上下逆さに注意。 　短周期 SRd は暗い　 　図２で周期 149 日以下の星の見かけ等級がライデンサーベイのサンプル中 では暗い方に片寄っていることに注意すべきである。もしもこれ等の星が 第１倍音であるなら、図２で長周期の星と同様にもっと明るい方まで見かけ 等級分布が伸びているだろう。 　SRd と Me の絶対等級　 　SRd と Me の絶対等級は Feast (1963) と Feast (1965) で議論されている。Me の絶対等級は Osvalds, Risley 1961 の 統計視差から、SRd は球状星団中の SRd から採られている。その結果は Feast (1965) 図１(b) に示されている。ただし、この論文では 47 Tuc にある ３つの 200 d Me （可視絶対等級 -3.0 mag）を考慮して、平均絶対等級は 短周期側で少し上がっている。

　４．変光星までの距離　

固有カラー　 　Kwee 1962 はライデンサーベイの銀河中心方向変光星のケープ SPg システム 等級を発表した。彼の観測した極大時等級は表２に示す。V　を UBV システム での等級とすると、 　　　　　V = SPg - 1.082(B-V) + 0.22 Smak 1964 は 27 Me 星の (B-V) カラーを示した。その平均値は 1.53 であった。 この値を Me の固有カラーと仮定する。 　星間吸収　 　サンプル星が位置する銀河面南側では星の分布がかなり一様に見える。斑な 吸収域が見当たらないことからも一様な吸収を仮定するのは妥当である。 McCuskey, Mehlhorn 1963 はこの領域の一般吸収を調べた。赤化は距離と共に 滑らかな増加を示し、uncorrrected modulus = 13.1 に対し、E(B-V) = 0.2 で ある。この　13.1 は今回のサンプル星の平均である。この値は b = -10, DM = 13 に対する銀河系星間吸収モデルからの予想値の半分である。しかし、この 領域は吸収が弱いことで選んだのでこの値は妥当である。この E(B-V) = 0.2, Av = 0.6 をサンプル星全てに適用する。こうして決めた距離を図３に示す。

図３．今回サンプル星の銀河面上分布。バツ＝ Se。黒丸＝ Me で |Vr| < 100 km/s. 白丸＝ Me で |Vr| > 100 km/s.

　５．Se 変光星　

　６．視線速度の解析　

第１倍音周期は基本振動に直す　 　Me 変光星の視線速度を解析するが、ここでは 149 日以下で基本振動と 看做される星も含めた。V947 Sgr は第１倍音振動として解析された。 脈動定数 2.4 を適用すると、この星は基本振動 348 日となる。太陽運動は (U0, V0, W0) = (10.1, 13.0. 6.2) km/s を使用する。U0 は銀河中心方向の成分である。 (GA の定義と逆に注意。 ) 　系統効果　 (i) 非対称ドリフト V = グループの平均回転速度と銀河回転速度との差。 (ii) 微分銀河回転 図４の負勾配の２直線は非対称ドリフト V = -100 km/s と -250 km/s に対する 効果を示す。破線は微分回転が (ω-ω0) = 25 km/s/kpc とした時の予想である。これは Feast, Shuttleworth 1965 によれば、 若い種族星の距離 r = 6 k pc (銀河中心距離 r = 4 kpc) に相当する。 Feast (1963) で、 Me 変光星の微分回転は太陽近傍では非常に若い種族より小さいことが 示された。なので、点線は r = 6 kpc での微分回転効果の上限と考えてよい。 この効果はより近い星ではもっと小さい。図４は、少なくとも l = [5, -5] の星では、非対称ドリフトと微分回転の効果は観測された視線速度区間に 較べ無視できるほど小さいことを示す。

図４．太陽運動補正後の Me 変光星視線速度と (sin l cos b) の関係。 上枠に b = -10 に対する l を目盛る。バツは r ge; 5 kpc. 点は r = [2, 5] kpc. 白丸は r ≤ 2 kpc. 点線は (ω-ω0) = 25 km/s/kpc の微分回転からの予想。二本の斜線は非対称ドリフト -100 km/s と -250 km/s に対する効果。

　７．|l| < 5 の Me 変光星　

　７．１．系統的運動　

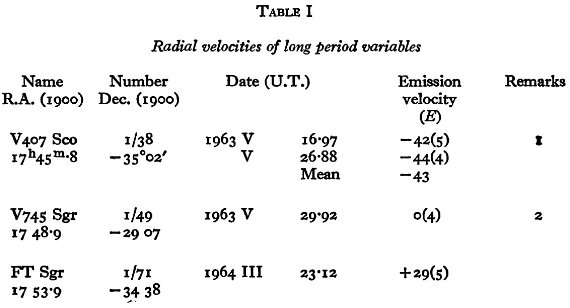
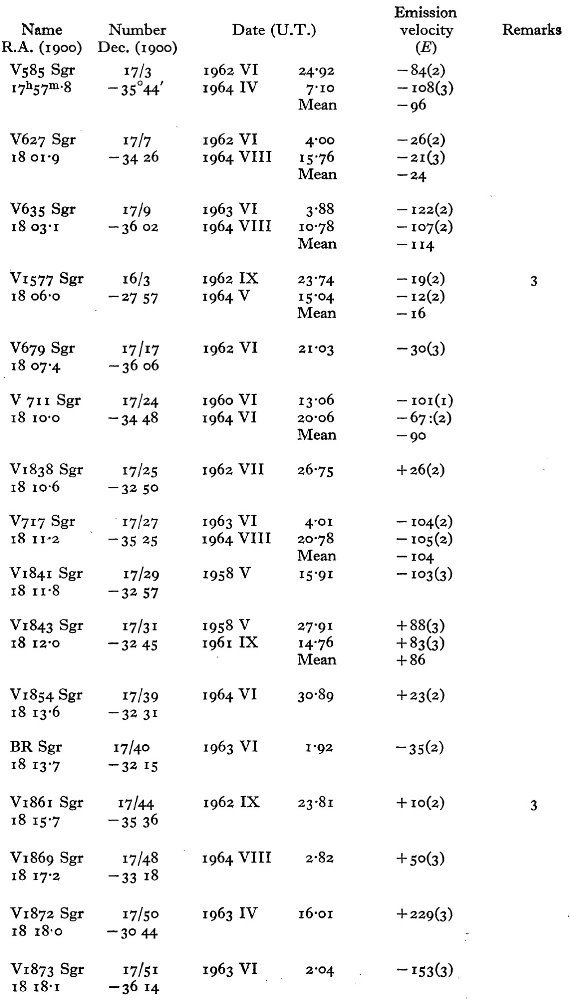
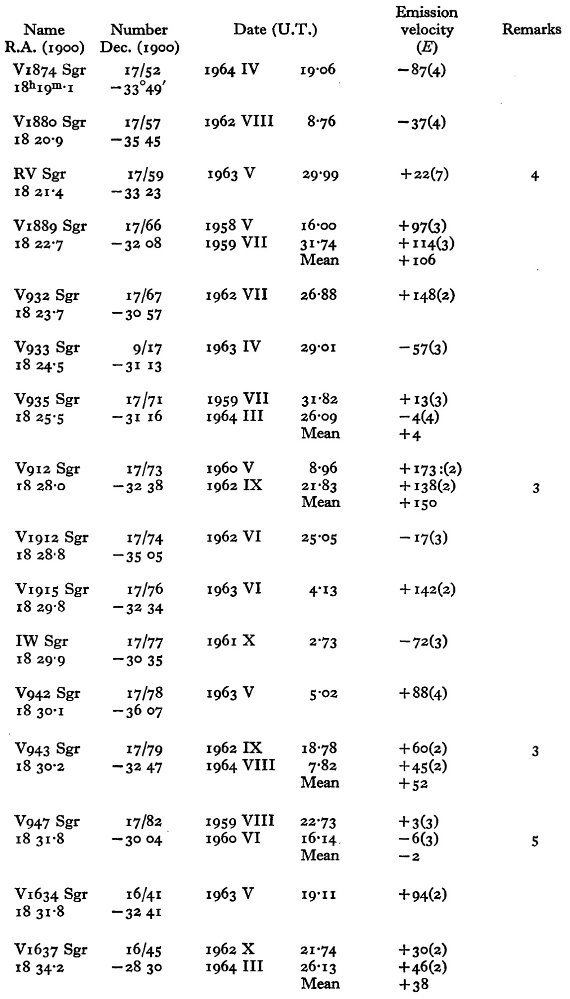
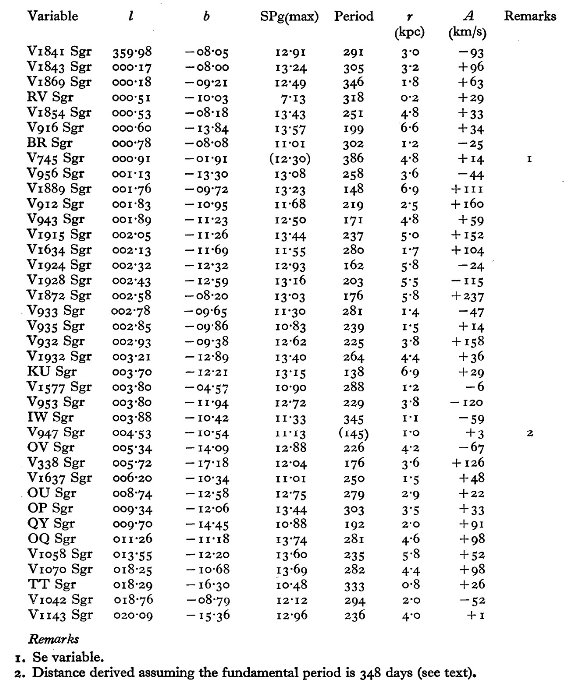
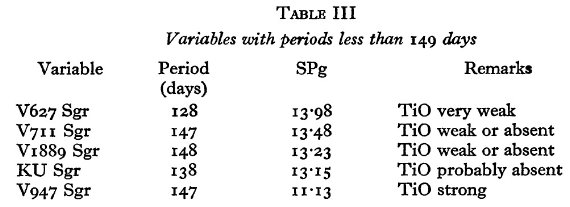
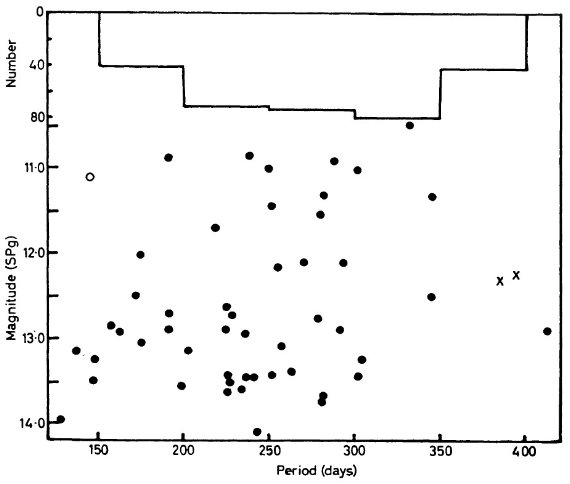
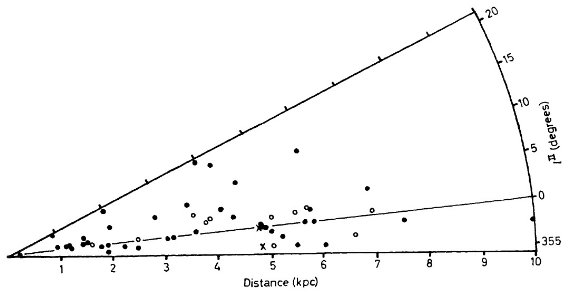
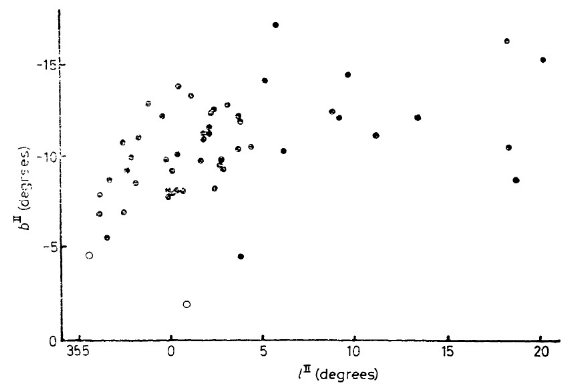
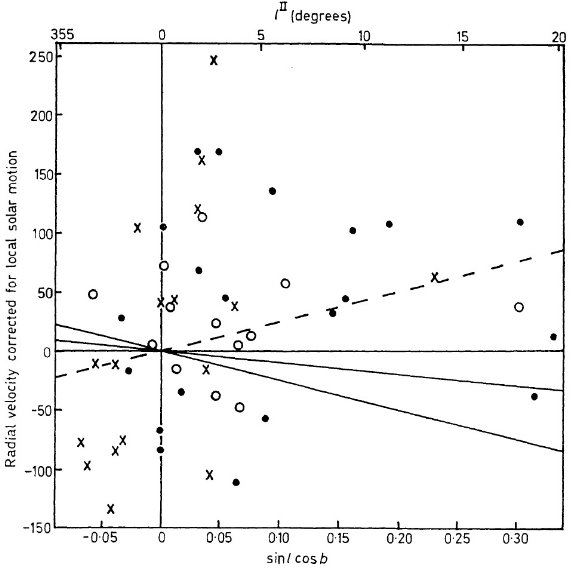
銀経による強い視線速度変化　 　図４には |l| < 5 で系統的な視線速度変化が現れている。特に遠方の星 に著しい。その極大は l = 2, マイナスでは l = -2 である。これは惑星状星 雲の結果と驚くほど類似する。Perek 1963 の図４には惑星状星雲視線速度と 銀経の関係が示されている。その著しい特徴は、銀河中心から銀経数度以内での 他所で見られないほど大きな速度分散と、系統的な中心速度の変化である。 視線速度の極大と極小が同じ銀経で生じているのも興味深い。 　ミンコウスキーによる PN の結果との比較　 　Minkowski 1964 は惑星状星雲の視線速度が銀経と共に系統的に変化すること を示した。彼はこれを銀河系微分回転の結果と考えた。もし直線 ρ = Vo sin l cos b を |l| < 5 の Me 変光星にフィットしたら、全 Me 星に対し ては Vo = 730 km/s が最少二乗解である。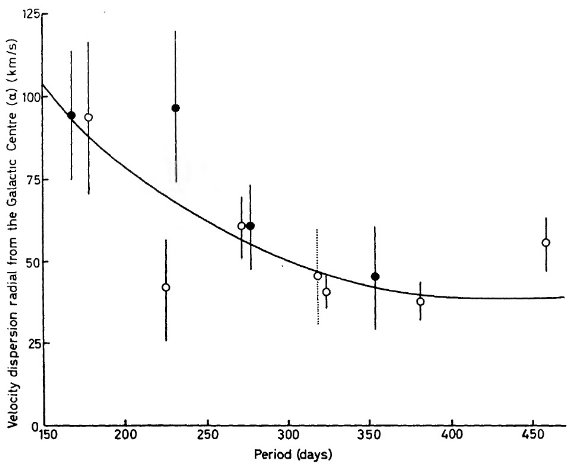これはミンコウスキーが PN に対し 得た 520 km/s に近い。しかし、短周期 P < 250 d のもっと遠い 22 変光 星は、Vo = 1240 km/s という大きく異なる値を示す。この結果を銀河系微分 回転で解釈しようとすると、 Vo = Ro(ω - ω0) と 言うことになる。図４の点線は Ro(ω - ω0) = 250 km/s に対するものである。微分回転がこの値より大きな Vo を生み出すこと は、特に非対称ドリフトの効果を上から差し引く場合、考えにくい。 惑星状星雲の距離は不明だが、大きな Vo を微分回転で説明するのは難しい。 (ω で剛体回転するサンプル 系を止めると、相対的に太陽は Vo = Ro(ω - ω0) で回転の接線方向に運動して見える。その太陽からは静止しているサンプル星 の視線速度は Vo sin l になる。ということ。 ) 銀河中心付近の星が大きな Vo　を持つ理由は次章で述べる。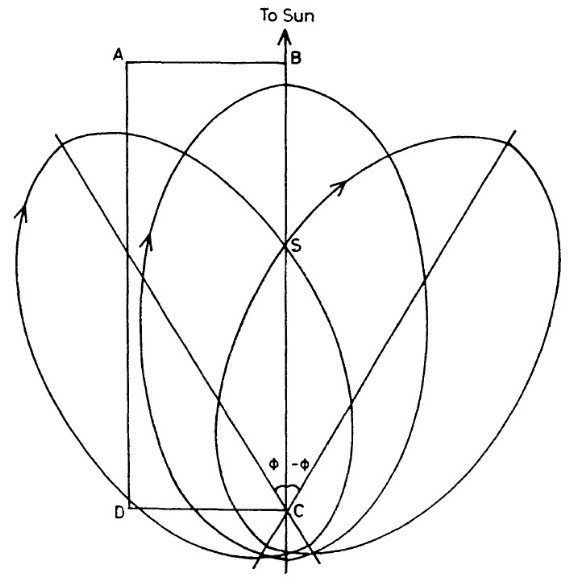 　軌道平均　 　図５のように２次元銀河で星が楕円軌道を運動すると仮定する。S 点において星の速度成分を (dR/dt, Rdθ/dt) とする。 軌道 主軸が CS に対し ψ 傾き、S 点で内向き、dR/dt < 0, の星 を考える。同じような軌道で主軸の傾きが -ψ の星は外向き, dR/dt > 0 である。もし多数の星が S 点付近で観測されたら、dR/dt 成分 の平均はゼロ、回転方向の平均速度は R dθ/dt となるだろう。しかし、 もしサンプルが太陽近傍よりかなり大きな区間から取られると, dR/dt の平均 がゼロになることは必ずしも自動的に保証されない。その時にはどの方向でも dR/dt がゼロでなくなる。図５はそれを初等的に説明している。図には、３つ の楕円軌道が描かれている。SC 線の片側領域 ABCD 内からランダムに星を選ん だとしよう。明らかに、選択される星はこの領域に滞在する時間が長い星に バイアスが掛かる。 (図５を使った説明が、内向き線と 外向き線の長さの比だけで外向きが優勢とするなら、無理がある。 まず、線の長さと滞在時間には速度が関係する。それから、太陽近傍では 内向きと外向きが相殺されると述べているが、それなら同じ理屈が、ABCD 領域 内の各点に適用できるはずで余剰は生じないはずである。) 　定向運動　 　上述の定性的な議論で、Me 変光星と PN の銀河中心方向に対して非対称に 見える視線速度分布は l < 0 側で外向き軌道優勢、 l > 0 側で内向き 軌道優勢であることに帰せられる。もしそうなら、Me と PN は定向運動を 行っている。さらに、平均回転成分 R(dθ/dt) は観測速度から直接に 得ることはできない。

図５．太陽・銀河中心線に対して異なる傾きをもつ３つの楕円軌道。 (左右の軌道は太陽近傍を 通過するが、中央軌道は太陽近傍を通らない。 ) 　K がゼロでない証拠は薄い　 　Me 変光星が銀河系中心に対し実膨張または実収縮しているかどうかは、 ρ = K + Vo sin l cos b を最少二乗フィットして決められる。 (K*r でなく, ただ K なのは サンプルの r がほぼ一定のためか？ ) P < 250 d の Me 星に対しては K = +10±21 km/s で、 Vo は K を入れない時の値とほぼ同じであった。P > 250 d の Me 星に対しては K = +16±13 km/s であった。K の正値は LSR が銀河系外側に動いてい ることを意味する。Kerr 1962 は H 21 cm の結果から K = +7 km/s を提案 している。また、ミンコウスキー 1964 は PN から K = +12.6±9.3 km/s を導いた。しかし、これらの値は太陽付近の Me 変光星に対して Feast 1964 が出した K = +3.8±3.6 km/s 程の精度はない。 K が ゼロでないという積極的な証拠はない。

　７．２．速度散布度　

表４＝ Me 変光星の速度散布度　 　表４には Me 変光星の速度散布度を周期区間別に示した。初めの２群は短周期 で平均距離が遠く、前節で議論したように著しい系統的運動を示す。散布度は Vo = 1240 km/s の平均速度の周りで計算した。長周期群は Vo がゼロでない 証拠が乏しい。散布度は太陽運動を補正したのみで求めた。 　α の計算　 　サンプル数が少ないので、散布度 α の計算は平均ランダム速度 に (π/2)1/2 を掛けて求め、特異速度の二乗は使わない。 ( 何のことか理解できなかった。) 　図６＝速度散布度と周期の関係　 　表４の速度散布度は図６にプロットされた。太陽近傍の星に対する速度 散布度は今回のデータからの値と一致する。 P = 230 d 付近で違いが見えるが 統計的には有意と言えない。 表４．周期区分毎の |l| < 5 Me 変光星の速度散布度

α は一定？　 　表４に示すように短周期変光星は銀河中心方向に 　6 kpc の距離に亘っている。そのように大きな距離に亘り α が太陽 近傍での値と大きく変わる証拠は見つからない。 星系の古典論では 定常状態で α は系全体で一定である。Kerr 1965 が注意したように、 Oort 1928 の回転銀河系での局所速度分布と密度勾配との関係は α 一定を前提条件とする。今回の研究は Me 変光星では与えられた周期に対し、 α が銀河系のかなりの部分で一定であることを示唆する。 図６．銀河中心からの動径方向速度成分の散布度 α と周期の関係。 黒点＝この論文の銀河中心方向の Me 変光星(表４)から求めた値。白丸＝太陽 近傍の Me 変光星( Feast (1963) 表５)。 垂直バー＝２σ エラー。太陽近傍の倍音振動 Me 変光星の速度散布度は その基準振動周期、破線でプロットした。

　８．PN 及び Me の速度散布度　

PN の速度分散　 　Perek 1963 が示したように PN の速度分散は銀河中心方向で非常に大きく、 その他の方向では穏やかである。これは銀河中心方向で α が急増する ことを意味し、前節で Me 変光星に対して述べたことに反する。Perek は PN を距離別に分け、その平均 |V| を求めた。 ⟨|V|⟩ は α(2/π)1/2 と取るべきである。 Perek は系統運動を無視している。彼の結果を表５に示す。 　PN と Me の比較　 　表５には |l| < 5 の Me を同じく距離別に分けた結果を示す。 距離による ⟨|V|⟩ の増加が PN と Me とで極めて良く似ていること が分かる。しかし、 Me では距離と共に平均周期も減少している。これは部分 的には短周期の Me ほど明るいためである。 (今も通用？ ) ７．２．節で述べたように、各周期区間に対する α は銀河中心距離の 広い範囲に亘って一定である。 　PN 非対称ドリフト　 　PN と Me に対する結果はほぼ同じである。ただし、PN 母星の年齢が狭い 範囲にあるという仮定は棄てる必要がある。太陽近傍の PN は非対称ドリフト -16 km/s で小さく、長周期 Me 変光星に近い。 Feast (1963) の表４では周期 300 日以上の Me 変光星はドリフト速度 -15 km/s である。

表５．|l| ≤ 5 の PN 及び Me の距離別の平均視線速度 　PN の種族が決まらない　 　一方では、Me 変光星に対する α が銀河面上広い範囲で一定と言う結論 を受け入れるなら、表５の結果は銀河中心付近で観測される PN は球状星団 と似た種族に特徴的な速度分散を持つことを意味する。すると、このような 特性を持つ PN は短周期 Me や SRd と似た種族と言うことになる。 PN の性質のこのような広がりは、物理特性の解明が進むまで待つ必要がある だろう。

　９． l > 5 の Me 変光星