銀河系楕円体

　２．星計数から楕円体光度関数を決める　

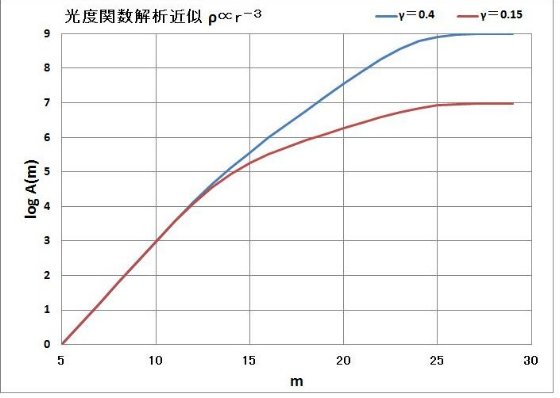
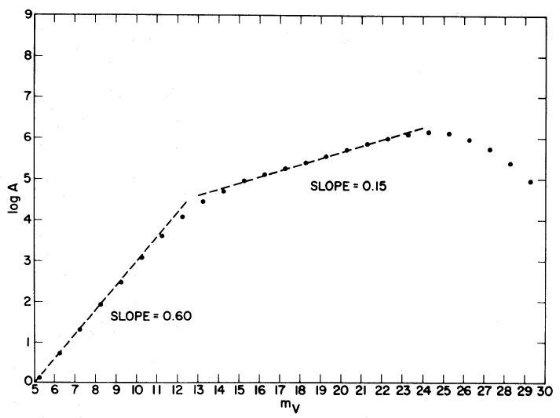
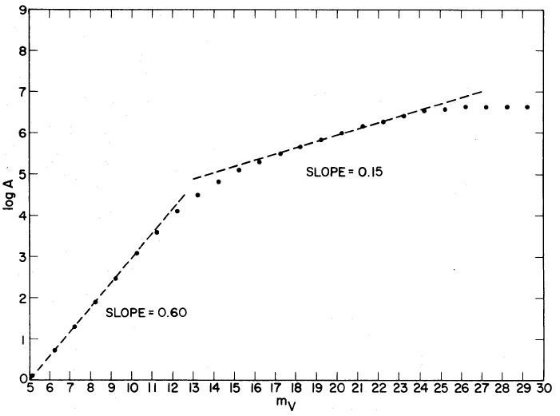
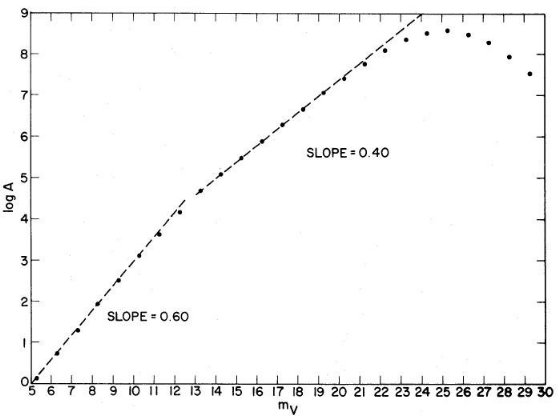
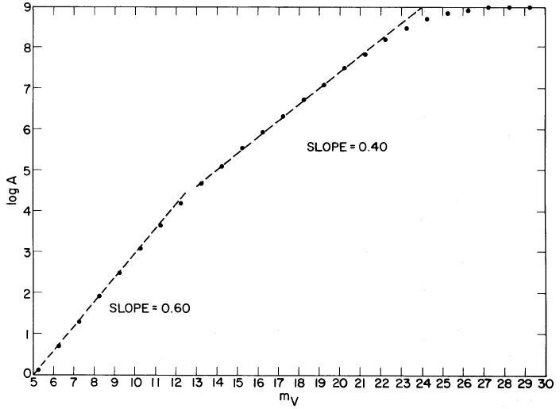
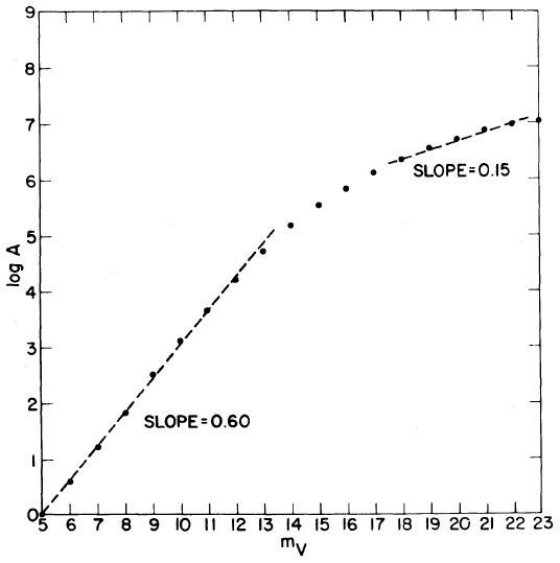
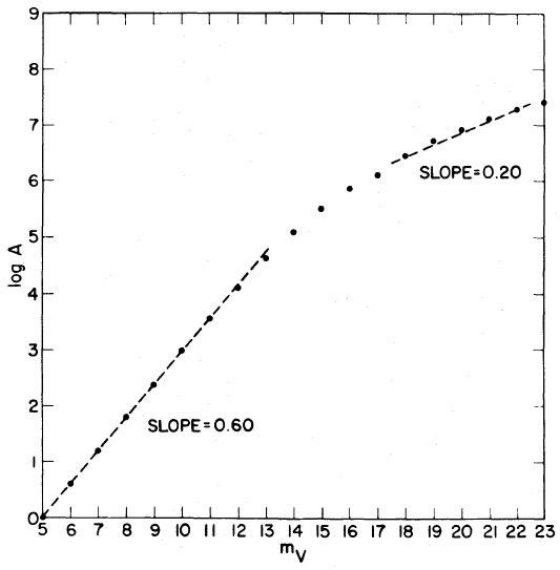
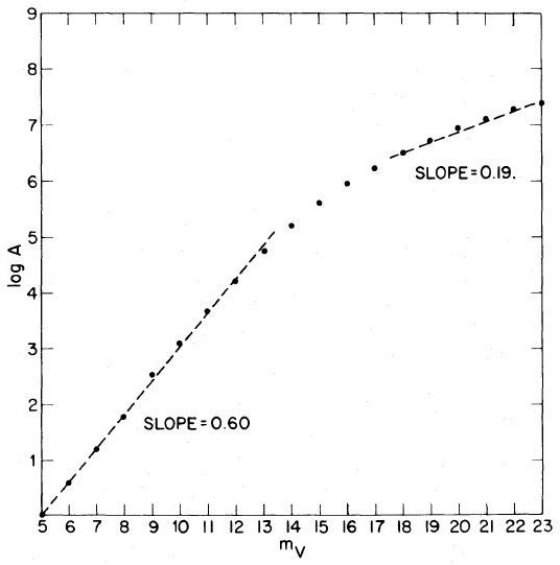
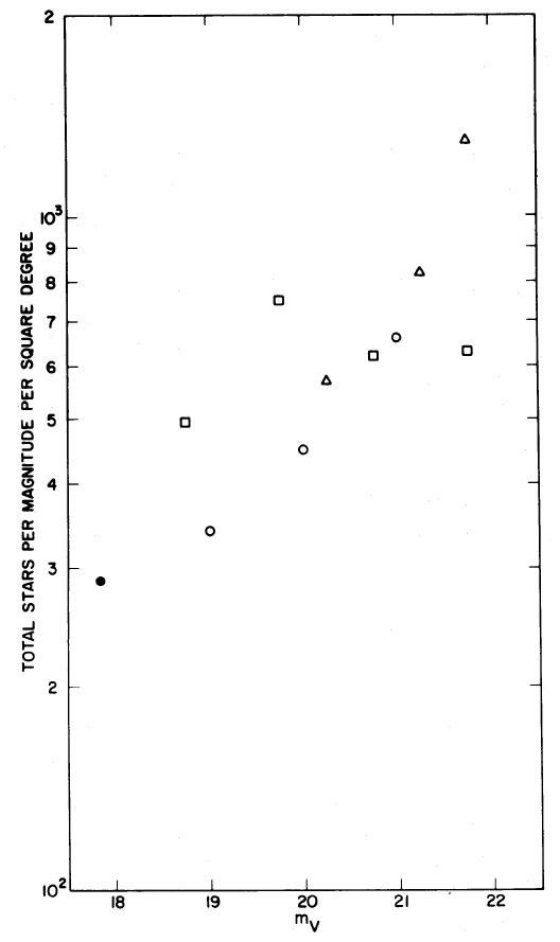
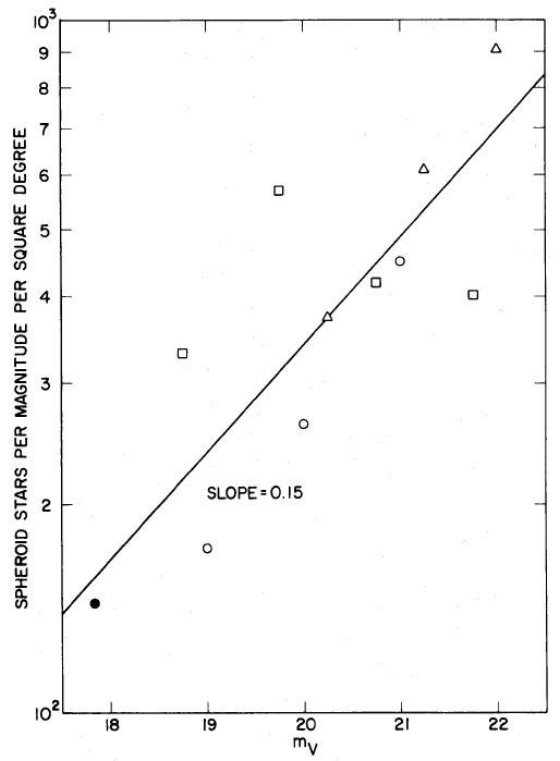
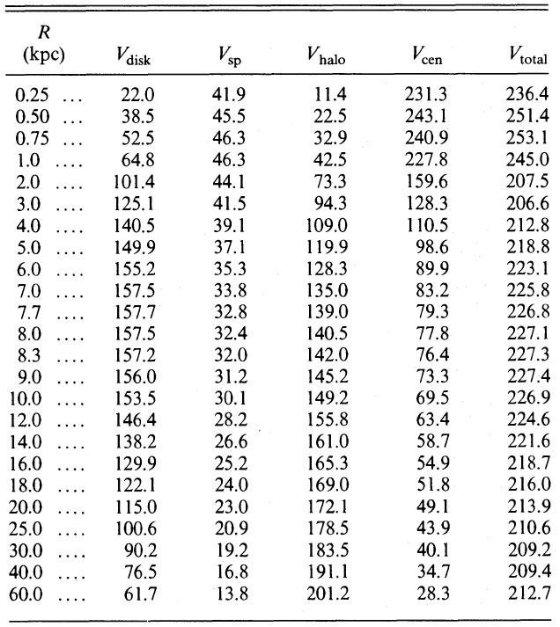
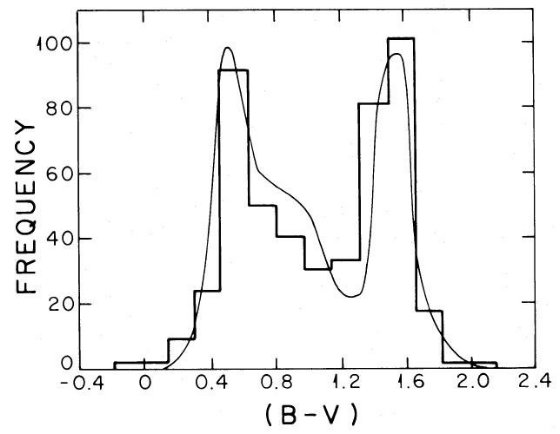
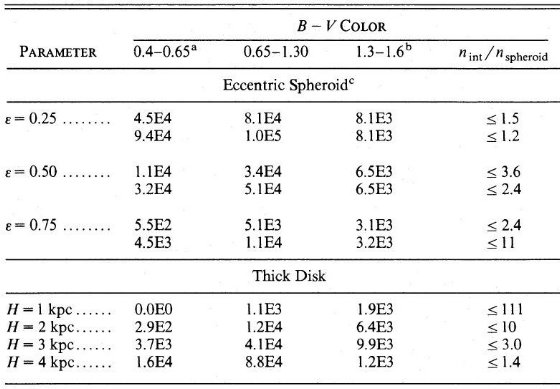
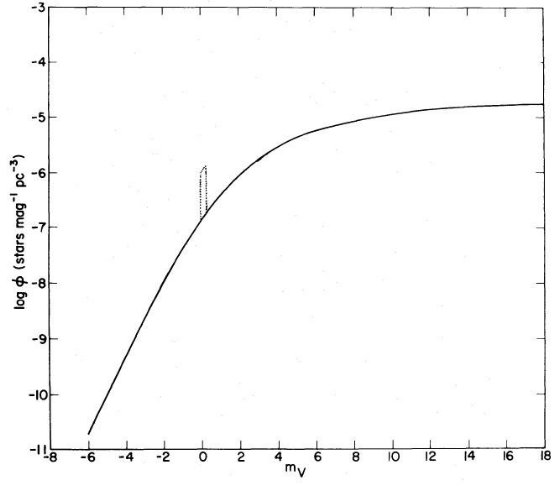
色々な量の定義　 　 Bahcall, Soneira 1980b は高銀緯での mV = 18 -22 等星計数から楕円体光度関数の傾き を決めることができることを述べた。単位ステラジアン、単位等級当たりの 星数密度, A(m), は 　　　　　 A(m) = ∫0∞dR R2ρ(r)Φ(M),　　　　　　　(1) ここにρ(r)は銀河中心距離 r での密度、R は太陽からの距離、 Φ(M) は等級当たりの光度関数である。r と R の関係は、 　　　　　r = (R02 + R2 - 2R0R cos b cos l )1/2　　　(2) 　光度関数は MB = 0 to -3 と MF = +10 to +15 の間で 以下のように表現されると仮定する。 　　　　　Φ(M) = Φ(M=0) 10+γM　　　　　　　　　　　　 　　　　(3) 　密度分布は 　　　　　ρ(r) = ρ0(R0/r)ν 　　　　　　　　　　　　　　(4) 　光度関数の式　 A = 10+γm A 0 ∫ XB dx x2-5γ 　(5) XF (1 + x2 - 2xcos b cos l )ν/2 ここに、XB ≡ [100.2( m + 5 - MB)] (1 pc/Ro)、 　　　　　XF ≡ [100.2( m + 5 - MF)] (1 pc/Ro)　である。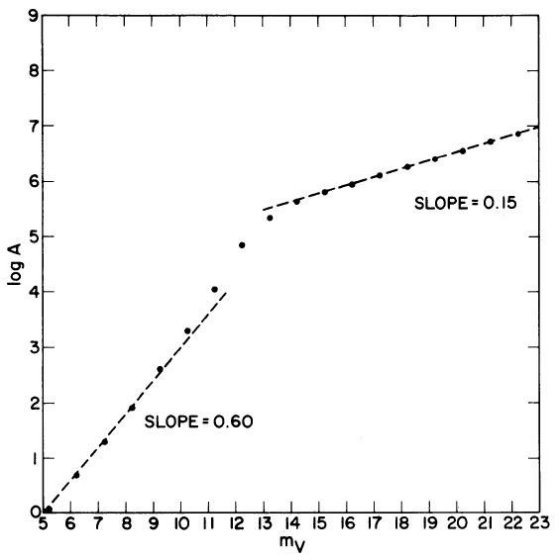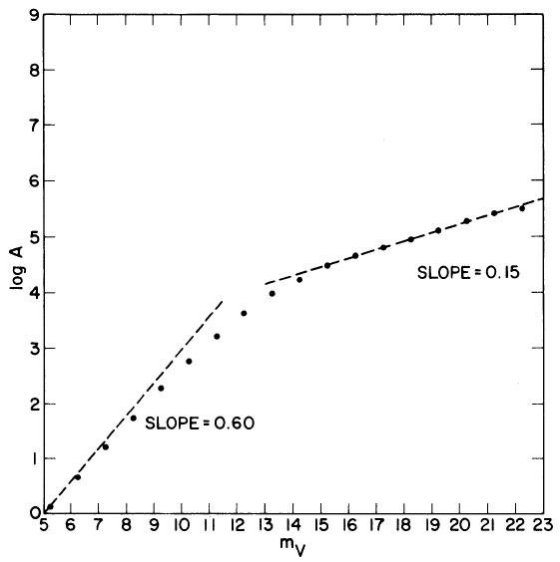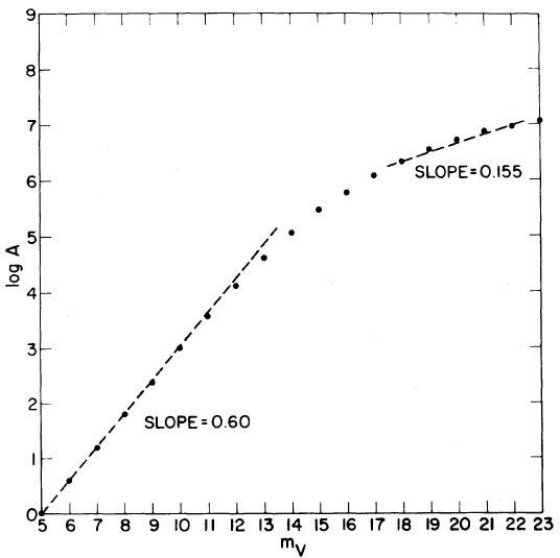 　明るい見かけ等級での近似式　 　明るい m （m が小さい）の場合、式 (5) の分母 = 1 と置けるので、結果は なじみの A ∝ 100.6m となる。この区間は XB ≤ 1 から、 　　　　　m ≤ 15 + MB である。MB = -3 とすると、m ≤ 12 となる。 分母 ∼ 1 は、銀極方向では (1 + x2)ν/2 ∼ 1 から、 x2(ν/2) ≪ 1 となるが、まあ大雑把に x ≤ 1 でもいいかということか。前段の計算を念のため書くと、 XB ≡ [100.2( m + 5 - MB)] (1 pc/Ro) ≤ 1 0.2( m + 5 - MB)-4 ≤ 1 m ≤ 15 + MB

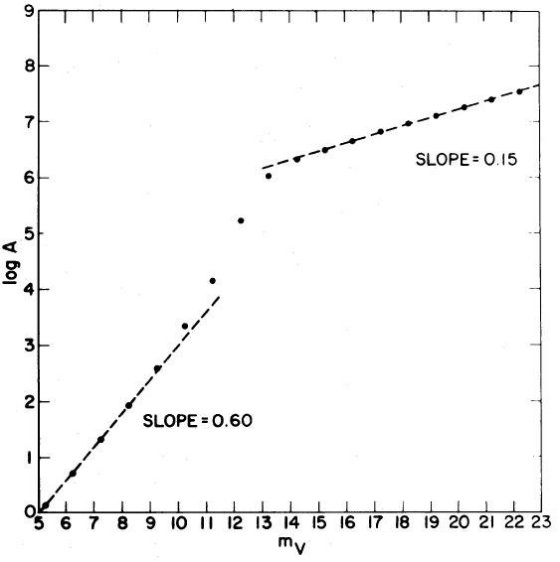
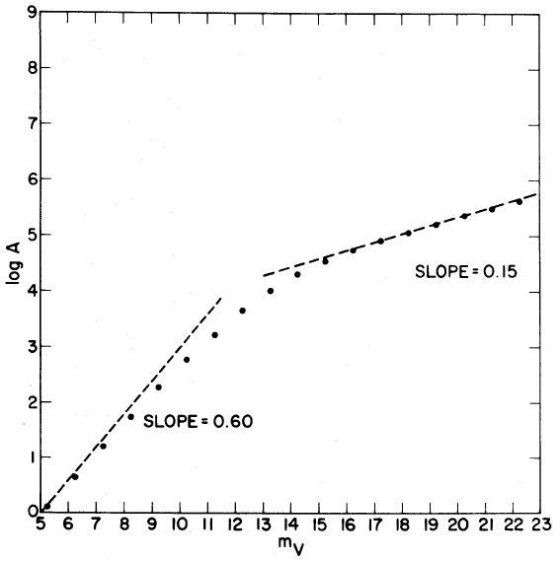
中間見かけ等級での光度関数　 　中間距離では、式 (5) の積分が定数となり、 　　　　　　　A ∝ 10γm 　　　　　(7) となる。この範囲を使うと星計数から光度関数の勾配を決定することが できる。 式　(5) の積分を見ると、 γ < 0.4 の時は極大を持ち、積分はその周り だけで決まって、m と無関係になる。それが上で言っていることの意味である。 それには厚み dR を一定にして比べた時に、積分への寄与が最大になる距離 Rmax が積分区間内にあることが条件である。被積分関数の極大を求めるため、x で 微分する。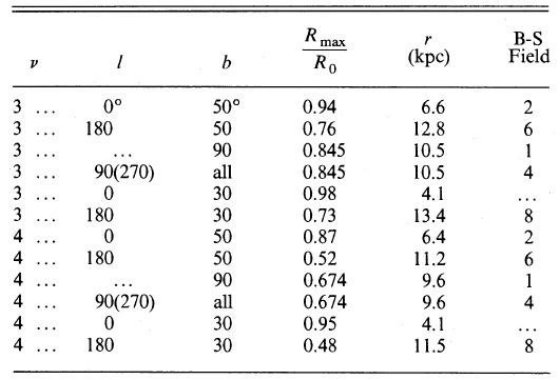α ≡ 2 -5γ, β ≡ (cos b cos l)/2 とし、 F' = α f g-ν/2 x-1 - (ν/2) f g-(ν/2)-1 (2x-4β) 　　= f g-ν/2 [(α/x) - (ν/2)(2x-4β)/g ] = 0 α(1+x2-4βx) - (ν/2)(2x2-4βx)=0 (ν-α)x2 - 2β(ν-2α)x - α = 0 xmax = β(ν-2α)+[β2 (ν-2α)2+α(ν-α)]1/2 (ν-α) Rmax = Ro β(ν-2α)+[β2 (ν-2α)2+α(ν-α)]1/2 　　　(8) (ν-α) 　表１．方向による Rmax の変化。論文には書いていないが γ = 0.15 である。(Check.xls に計算してある)

　Fig 1 を確認する。　

そこで、log [A(m)/A(m=5)] を /Fotran/LF/LF1.f で計算して、Fig 1 (c),(d) をチェックすることにした。結果は下のようで、確かに論文と一致した。 図　ν = 3 の極方向光度関数

　星計数の解析表現について考えてみた　　

下の図で、面上に LF(M)*G(R)*R^3 の星数密度が分布している。その上を 斜めの m = const 線に沿って積分すると星計数 SC(m) が得られる。 　明るい見かけ光度＝近距離＝等密度　 　この時、上の密度変化 G(R) = 1 なので、下の２本の m = 一定線を比べると、 M で積分の際に R^3 項だけが 100.6m 分変化する。これが星計数 になるので、SC(m) = 100.6m*定数　となる。 　密度変化がある時は　 　密度変化がある時は SC を求める積分の際に、 m = 一定線分上で G(R)R^3 に極大が生じることがある。LF(M) = LF(M=0)10γM とすると、M=m-5logR+5 を使って表式を戻して、 　　　　　SC(m) = 10γm∫LF(5-logR)*G(R)*R^2dR となる。積分範囲内にピークが含まれていれば積分値はほぼ一定になる。 その結果、SC(m) = 10γm*定数　となる。 積分範囲は、100.2(m+5-MF) pc < R < 100.2(m+5-MB) pc である。したがって、非常に暗い 、m が大きい、所ではこの条件から外れ、積分がピーク外で行われるため 低下して行く。

　第２章真ん中あたり　本文の続き　

　３．数値シミュレーション　

図１a. 極方向、球対称ドボークルー型密度分布, γ = 0.15 に対する星計数 図１c. 極方向、球対称ハッブル型密度分布, γ = 0.15 に対する星計数

図１b. 極方向、球対称ドボークルー型密度分布, γ = 0.4 に対する星計数 図１d. 極方向、球対称ハッブル型密度分布, γ = 0.4　に対する星計数

図２a. ドボークルー型密度分布, γ = 0.15, だ円率ε = 0, b = 20°,l = 0° 図２c. ドボークルー型密度分布, γ = 0.15, だ円率ε = 0, b = 20°,l = 180°

図２b. ドボークルー型密度分布, γ = 0.15, だ円率ε = 0.5, b = 20°, l = 0° 図２d. ドボークルー型密度分布,γ= 0.15, だ円率ε= 0.5, b = 20°,l = 180°

円盤の光度関数を用いて計算した例 　図３は簡単のために、円盤の光度関数を用いて計算した例である。その表式は、 Φ(M) = 定数 × 10β(M-M ∗) 　　　　　　(16) [1 + 10-(α - β)δ (M-M∗)]1/δ この光度関数の形を図４に示した。図のパラメターは円盤の標準光度関数として、 このシリーズで採用しており、 M∗ = +1.28, α = 0.74, β = 0.04, δ-1=3.40 である。図３a, b では Φ(M) として、 図４の光度関数を -3 ≤ M ≤ +10 で採用した。その外では Φ(M) = 0 である。図４で示した種族 II 光度関数は、 Schmidt 1975 が +6 &le: Mpg ≤ +12 で求めた楕円体光度関数をよく表現 しており、また、サンデージ(1954) が M 3 の -3 &le: MV ≤ +6 で求めた楕円体光度関数とも似ている。 ただし、図４の光度関数は MV > +6 で、下田、木村　1970 の M 13, Hartwick 1970, van den Bergh 1975 の M 92 光度関数と比べるとより緩やかである。例えば、 M 92 では +4 ≤ MV ≤ +8 で γ = 0.21 であるが、 星計数の傾き、式 (17)、 から得られた値は γ = 0.15 である。ただ、 先で示すが、現在の星計数データと高速度星データから決まる楕円成分の 傾きは &plusmd;0.035[1σ] の誤差を含む。 　水平枝の寄与　 　図４には水平枝が光度関数に寄与する場合も考えた。知られている最大の寄与 が M 92 で Tayler 1954 により報告されている。その値を採用して、 MV = 0.0 を中心とする ΔM = 0.25 の区間で星の数を 6 倍に 上げた。 　図３の勾配変化　 　図３(a) はドボークルー密度則に図４の円盤光度関数を与えて計算した。 　図３(b) はハッブル密度則に円盤光度関数を与えて計算した。 　図３(c) はドボークルー密度則に円盤+水平枝光度関数を与えて計算した。 　図３(d) はハッブル密度則に円盤+水平枝光度関数を与えて計算した。 図３の勾配を見ると、15 ≤ m ≤ 19 で γ = 0.3 から　 19 ≤ m ≤ 22 で γ = 0.15 へと変化する。この勾配変化は 図４光度関数の勾配が連続的に変化して行くことを反映している。 γ = 0.15 が起きるのは MV = +5 の付近である。 　ハッブル則だとドボークルー則より急になる　 　同じ見かけ等級で比べると、ハッブル則はドボークルー則よりもやや急な 勾配を与える。これは、ハッブル則の方が密度の落ち方が緩く、したがって ある見かけ等級レベルではより明るい星を見るためである。

図４．実線＝式(16) の円盤光度関数。点線＝水平枝を付加、図３c,d に使用。 　その勾配の差、γHubble - γde Vaucouleur は 18 ≤ mV ≤ 22 で 0.04 である。 　水平枝の寄与　 　図３を見ると水平枝の寄与は無視できる程度であることが判る。 　データ精度による限界　 　楕円体の星計数が広い等級帯に渡り高い精度で得られれば、光度関数に関して 大きな情報を得ることが可能である。しかし、次の章で見るように、現在の データ精度ではある限られた等級帯での有効勾配を得るのが限界である。

図３a. 極方向、球対称ドボークルー型密度分布, 円盤光度関数の星計数 図３c. 極方向、球対称ドボークルー密度分布,円盤+水平枝光度関数の星計数

図３b. 極方向、球対称ハッブル型型密度分布, 円盤光度関数の星計数 図３d. 極方向、球対称ハッブル型密度分布, 円盤＋水平枝光度関数の星計数

　４．楕円体成分の密度と光度関数の決定　

４．a. 18 ≤ mV ≤ 22 での星計数　 　楕円体成分の抽出　 　18 ≤ mV ≤ 22 での星計数観測結果が図５(a) に示されている。 ベル研の 22 ≤ mV で星計数が急増するという結果は載せていない。 銀河の混入の可能性が強いからである。観測値 Aobs からモデルで計算した円盤星 の寄与 Adiskmodel を引いた後の楕円成分の星計数 Asph = Aobs - Adiskmodel が図５ (b) である。Asph が極方向の 4 < mV < 16 で予想と よく合っている、 Bahcall, Soneira 1980b の図４(a) と Bahcall, Soneira 1981a ApJ 246, 122 の図１ を見よ、 こと、それから SA 57 と SA 68, Kron 1978, の 19.75 < mV < 22.0 でのカラー分布、 Bahcall, Soneira 1980b の図８を見よ、は円盤モデルの予想が正しいことも示唆している。 　円盤星の割合　 　計数中で円盤星が占める割合 F は、F(mV=18) = 0.5, F(mV=19) = 0.3, 、F(mV=20) = 0.3, 、 F(mV=21) = 0.25, 、F(mV=22) = 0.18 である。 もしも銀極付近 1 deg2 の領域で mV < 22 のカラー 測定が行われていれば、円盤星の差し引きは要らないかもしれない。 図５ a. 銀極方向星計数(mag-1deg-2)。 補正なしデータ。 黒丸＝Sears et al 1925, 三角 = Kron 1978, 白丸 = Tyson, Jarvis 1979、 四角 = Peterson et al 1979、

Φ(MV) の決定　 　現在のデータでは γeff のやや粗い見積もりが得られるのみ である。図５(b) に最小二乗フィットを行った結果は、 　　　　　　　γeff = 0.145 ±0.035 (1σ) 　　 　　　　　　　　　　　　　　　(17) であった。 　図５(b) は楕円体光度関数の決定にも使われる。星計数から楕円体光度関数 ( +4 < MV < +8 ) が定められる等級帯から、 　　　　　　　Φ(MV) = 4.3(1±0.2)×10-6 100.145(MV-6)pc-3mag-1 　　　(18) 　星星数から得られる量の意味　 　式 (18) は太陽近傍の値で表現されている。これは高速度星から得られた 光度関数、 Schmidt 1975 と比較するためである。しかし、星星数から得られる量は典型的には銀河面から 高度 5 kpc 以上での楕円体成分の平均値である。高度 z ≈ 5 kpc での密度 は、式 (12) のよると銀河面での値の 57 % である。 図５ b. (a) からモデル円盤成分を引いた残り＝楕円体成分。直線は式(18)。

星計数に寄与する絶対等級の範囲　 　表２には 18 < mV < 22 星計数中での楕円体星と予言される 星の数の割合を示した。この見かけ等級帯に寄与する星の大部分は +4 < MV < +8 の星から来る。ドボークルー密度則を仮定した 場合、 18 < mV < 22 では楕円体成分の星の 84 % は +4 < MV < +8 （ハッブル則では 70 %）である。これらの結果 は Bahcall, Soneira 1980b において、 Kron 1978 の　19.75 < mV < 22 データを用いて 確認された。 　もっと急勾配？　 　Shanks, Phillips,Fong 1980 は極方向の星計数から γ = 0.34 を 出している。この結果は　20 < J < 22 データに基づいている。その帯域 には星の１０倍も銀河が存在する。かすかな点状に見える銀河の仕分けを 8 % 間違えただけでこの結果が導かれるのである。我々は、もっと明るくて、分類が 問題にならない領域でこの問題を扱った。

表２． 18 < mV < 22 星計数中での楕円体星の割合。 　　　　水平枝星は含んでいない。

４．e. 楕円体密度の評価　　 　光度関数をデータでカバーできる範囲　 　４(a), (b) では等級範囲を、星計数に関しては +3 ≤ MB ≤ +8, 固有運動解析に対しては +6 ≤ MB ≤ +11 に限った。これは データが入手できる範囲だからである。しかし、楕円体の数密度、光度、質量に 大きく寄与するのはこの範囲外の星である。我々は範囲外の光度関数に対し、 円盤光度関数と同じ(Bahcall, Soneira 1980) とか質量関数をべき乗則(Schmidt 1975) と仮定したりしてきた。 　様々なモデルで得た楕円体密度　 　表３は幾つかの等級帯で、楕円体成分の数密度 n, 質量密度 ρ を示した。 星計数に基づく楕円体密度評価には、（１）円盤光度関数、（２）γ = 0.15 べき乗則光度関数（α=1.6 質量関数）、（３）高速度星 G ∝ M -α, α = 1.0、（４）高速度星 α = 2.0 の各場合に ついて計算された。水平枝星の寄与は無視できる。円盤光度関数の適用では 大きさを 1/800 にしてある。質量光度関係は (1), (2) では Bahcall, Soneira 1980 を (3), (4) は Schmidt 1975 の関係を用いた。 　数密度、質量密度　 　水素燃焼質量 (M > 0.085 Mo, Mv ≤ 16.5) 以上の星の総数を上の モデルについて計算すると、 　　　　　n(Mv ≤ 16.5) = (1-9) 10-4 pc-3 　　　　　　　　　(23) 　　　　　ρ(Mv ≤ 16.5) = (4-14) 10-5 Mo pc-3 　　　　　(24) 　楕円体密度の不確かさの理由　 　楕円体密度の不確かさには幾つかの理由がある。 （１）データが得られる 4 ≤ Mv ≤ 11 は星質量全体の 1/2 - 1/3 に過ぎない。 （２）星以下の質量の天体の可能性 　光度密度　 　光度密度には巨星が貢献すると考えられるが、現在得られているデータでは それらの星の情報が少ない。銀極方向の星計数からは光度関数が Mv = +3 で終わっていてもデータと 20 % 範囲で矛盾しないという結果が得られている。

表３．楕円体成分密度関数のパラメター 　M 92, M3 の光度関数から Mv = 5.5 - 6.5 の星に対しては M/L = 15 と 54 を得た。これを光度関数 (18), (21), (22) と組み合わせて、 　　　　　Lv(spheroid) = (2-8) 10-5 Lo pc-3 (星計数) 　　　　　　　　　　　　= (3-13) 10-5 Lo pc-3 (高速度星) を得る。Bahcall, Soneira 1980 モデルでは 7.7 10-5 Lo pc-3

　５．銀河回転曲線　

回転曲線から楕円体質量を決める Caldwell, Ostriker モデル　 　Caldwell, Ostriker 1981 は回転曲線上に６点を選び、楕円体にハッブル則に 似た密度分布と一定の M/L 比を仮定して、適当な解析近似式を適用して、近傍 楕円体密度に 1.1 10-3 Mo pc-3 を得た。この値は 前節で得た値、(4-14) 10-5 Mo pc-3 よりずっと大きい。 　この大きな値はもしも質量の大部分が前節で扱わなかった低質量天体に含まれ ていると考えれば前節と両立する。 　しかし実際には、Caldwell, Ostriker は R ≤ 2 kpc という近距離で観測さ れる大きな速度を純粋に回転運動と看做すことを大きな楕円体局所密度の根拠に している。しかし、そこは伝統的な円盤とハローがあまり有効ではない領域である。 もしそのような論理を立てなければ大質量楕円体の根拠は弱くなる。 　別モデル　 　楕円体にドボークルーモデルを適用し、中心部には Oort 1977 のモデル、 楕円体と中心成分の光度密度にかなり誤差があることを考慮して、 M/L 比は 一定と仮定する。中心部分の密度分布はオールトに従い r-1.8、 軸比 0.4 とした。この中心成分は r = 1 kpc で断ち切られるとする。 　我々は Caldwell,Ostriker の回転曲線とのよい一致を得た。これは楕円体 密度を大きくする必要が必ずしもないことを示す。４成分の密度則は Bahcall, Schmidt, Soneira 1982 の表１に示されている。それによると、 太陽近傍での総密度は 0.15 Mo pc-3 である。 図６．４成分回転曲線＝Oort提唱の中心構造＋円盤＋楕円体＋大質量ハロー。 菱形は Cadwell,Ostriker 1981 の付けた拘束

円盤はスケール長 3.5 kpc, 太陽の銀河中心距離は 8 kpc, スケール高や光度関数は近傍観測 で得られたものを適用した。楕円体はドボークルー密度分布に従い、 その規格値は 0.00125 である。大質量ハローには、局所ハロー密度 0.009 Mo pc-3, コア半径 2 kpc, 密度 r-1.8 とした。 星間ガスはスケール高 125 pc である。 　各成分からの回転曲線への寄与　 　図６の菱形は Caldwell, Ostriker による制約である。円盤と中心成分 による回転速度は Freeman 1970 と Schmidt 1965 の方法で数値的に求めた。 球対称楕円体とハローの寄与は密度を積分した半径内質量から決まる。表４に その結果を与えた。得られたオールト定数は A = 13.8 km/s/kpc, B = -14.3 km/s/kpc, 太陽回転速度は 225 km/s である。 表５．銀河系回転曲線への各成分の寄与

　６．中間スケール高種族　

中間種族　 　高速度星の研究から導かれた楕円体密度　Schmidt 1975 はこれらの星の 直交速度の中間値は 250 km/s であるという仮定に基づいていた。この 速度は極端種族 II に対応する値である。中間スケール高種族の星は もっと小さい速度を有するのでこのサンプルからは除外される。しかし、 1957 年のバチカン会議では中間種族が認められ、Plaut 1965 はそれに 属する変光星を記述した。 　双峰性カラー分布　 　Bahcall, Soneira 1980 は暗い星のカラー分布に現れる双峰性を円盤種族 と極端楕円体種族からの寄与の重なりとして解釈した。この２成分モデルは 銀河の観測とも合致する。しかしながら、少なくとも幾つかの銀河には 第３成分が存在する　Tsikoudi 1977, Burstein 1979 という報告がある。 　第３成分の不在？　 　この節では、Kron の２色観測では中間スケール高成分が現れなかった ことを用いて、5 ≤ Mv ≤ 8 の等級帯においてこの成分の上限を 求めよう。光度関数はこの成分にも円盤光度関数を仮定する。 図７の解釈では、赤いピークは急な密度減少のため近距離の暗くて赤い星を 主体にした集団である。円盤の明るく青い星がこの見かけ等級帯に入るには 銀河面から遠く離れる必要があり、円盤密度の減少からそのような星は 殆ど存在しない。一方、密度減少が緩い楕円体成分は比較的遠方の固有 光度が明るい青い星が体積効果により暗い見かけ等級帯に現れることを 可能にする。図７には標準モデルの予想を実線で示してある。 B-V = 0.65 - 1.3 のへこみは円盤と楕円体の中間スケール高を持つ種族が 存在しないことを示している。このギャップは 5 ≤ Mv ≤ 8 に 相当している。

図７．銀極方向、19.75 ≤ V ≤ 22.0 星の B-V カラー分布。ヒストグラム は Kron1978 の観測、曲線は標準モデル。 0.65 ≤ B-V ≤ 1.3 の谷間が 中間スケール高種族の上限を定める。

２種類の密度分布　 　ここでは２種類の密度分布を考察する：一つは厚い指数関数型円盤で スケール高 H が 2 ≤ H ≤ 4 kpc, もう一つはドボークルーまたは ハッブル則の扁平楕円体で 0.25 ≤ ε ≤ 0.75, ここに ε = 1 - κ で κ = 軸比である。表５には Kron SA 57 サンプル中に中間種族星が何個現れるかを示している。この種族の 太陽近傍における規格値は最初円盤種族星と同じにされた。 　中間スケール高種族の上限値　 　中間スケール高種族の上限値は、 0.65 ≤ B-V ≤ 1.3 の観測値 152 星を倍にする近傍密度として定義される。ε = 0.50, または H = 3 kpc モデルはギャップの中間でカラー分布がピークに達する。 従ってこのモデルに対して上限値を見てみよう。すると、0.003 ndisk だと観測カラー分布の窪みを埋め、従って排除されることが判る。この 上限値は楕円体密度の３倍である。表５を見ると、密度勾配とカラー分布 に相関があることが判る。ハッブル楕円体の密度分布 r-3 は ドボークルー楕円体の r-4 より緩い。したがって、与えられた 楕円率 ε では赤い方、つまり暗くて近距離、の星計数は殆ど同じ だが、青い方、明るくて遠い星、では著しく異なる。

表５．中間種族のカラー分布

　７．まとめ