Arenou92

A Tridimensional Model of the Galactic Interstellar Extinction

Arenou, Grenon, Gomez

1992 AA 258, 104 - 111

　アブストラクト　

　現存のスペクトル及び測光データを全て用いて、全天の星間減光をマップした。色超過分布を (l, b, r) の関数としてモデル化した。

　このモデルは色超過が得られない高銀緯に有用である。

　２．データ　

表１．MK-分類のある星の数 (26,052 星）

　INCA　データベース　

　INCA データベースは 215,000 星を含む。Hipparcos Input Catalogue の準備の際に、SIMBAD からの分光データも全て取り込まれた。最終的には 77,000 星が MK スペクトル分類を、 94,000 星に HD スペクトル分類が与えられた。

表２．HD-分類のある星の数 (16,569 星）

　MK 分類のある星を使った。

　最終サンプルからは変光星、10" 以内の連星を除いた。INCA データベースの星は V = 13 よりは明るい。MK 分類のある星が星間減光モデルを作るのに使われた。

　３．星間減光モデル　

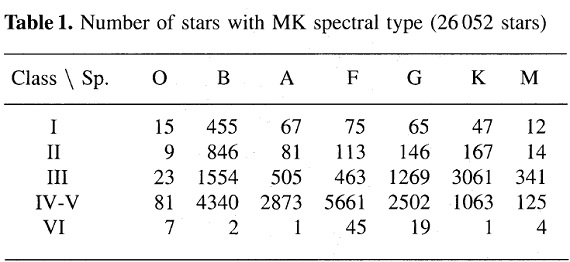
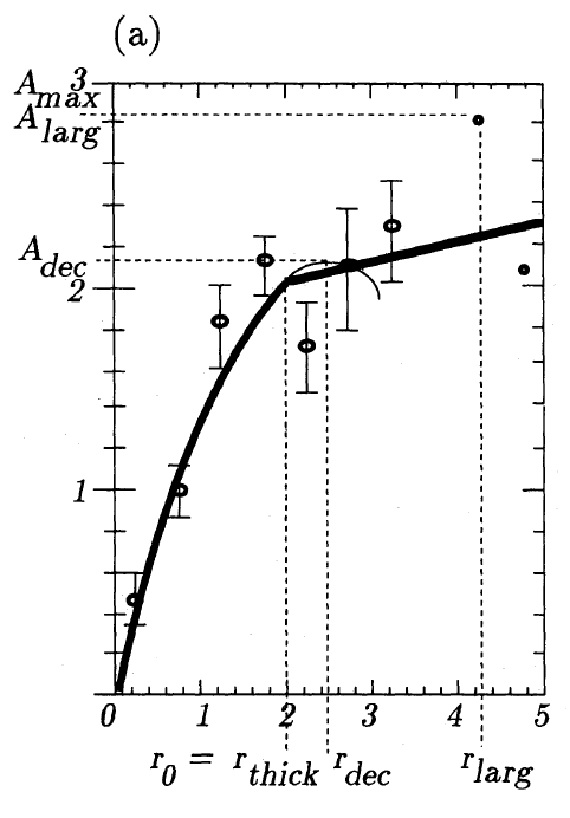
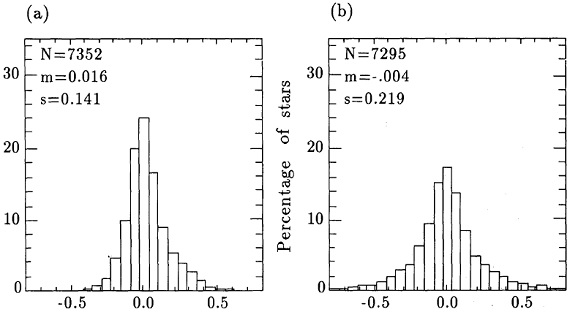
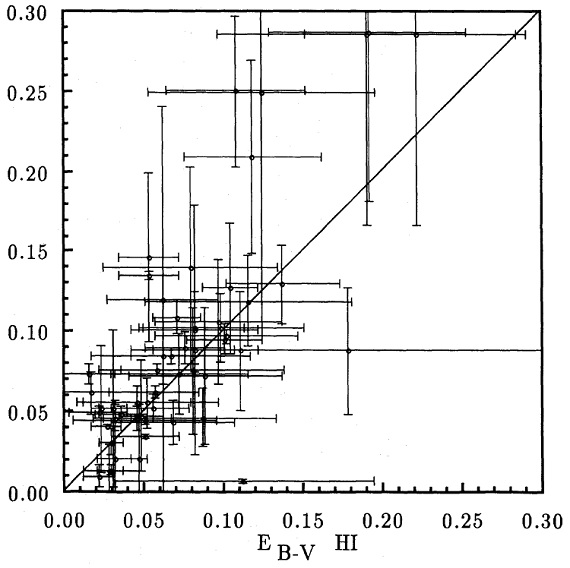
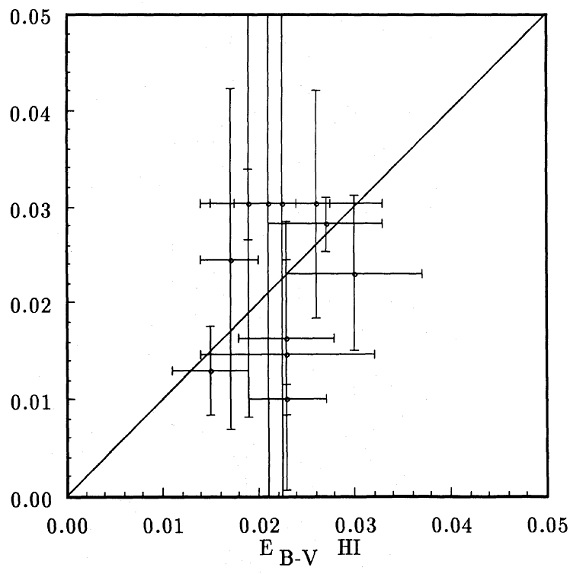
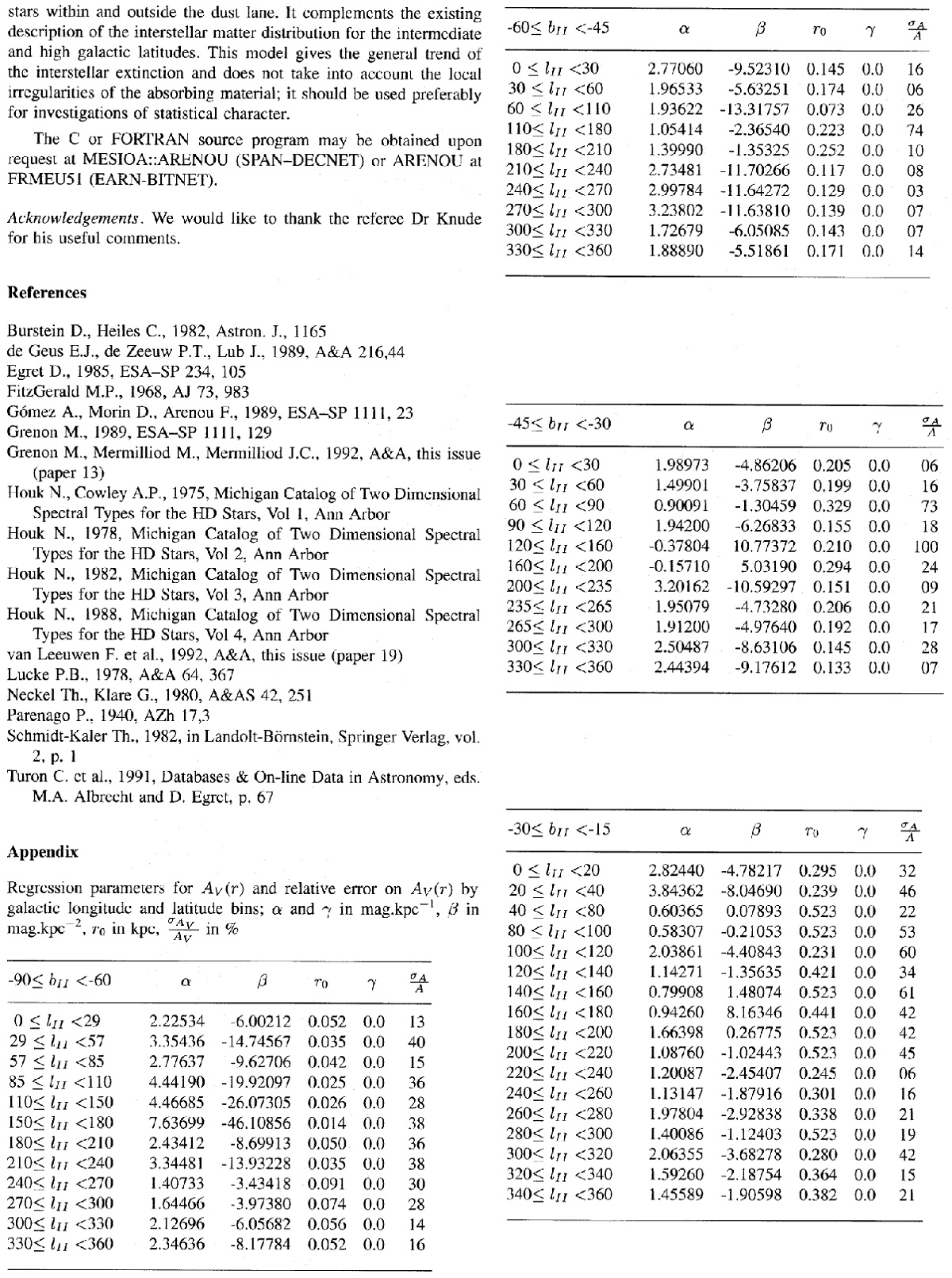
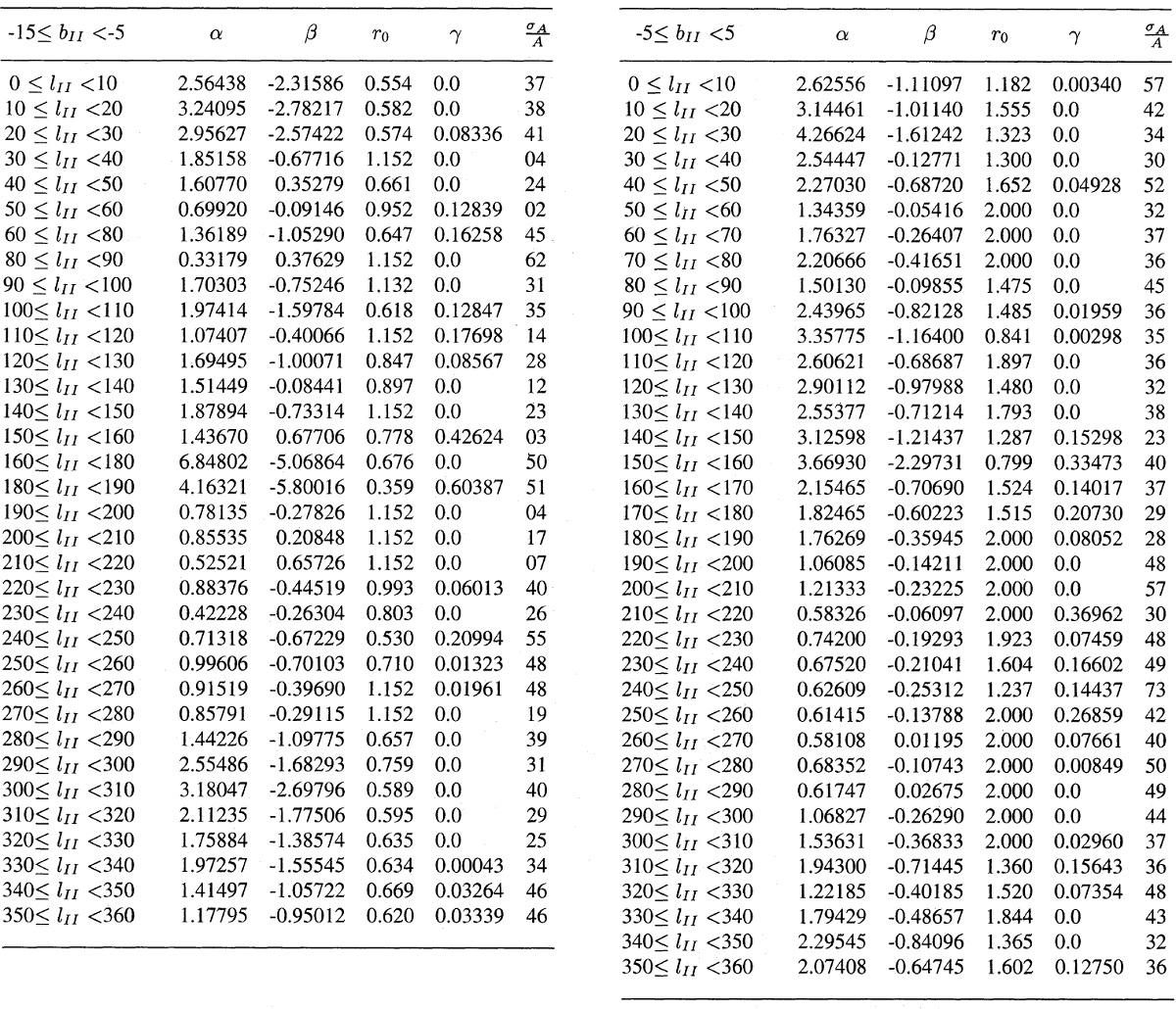
図１a．l = [180, 190], b = [-5, 5] の Av-D 関係。ビン＝500 pc.

　Av と　r の導出　

　各星毎に減光を以下の式で求めた：

　　　A_V = R E_B-V

　　　E_B-V = (B-V)_ph - (B-V)₀

　　　R = 3.30 + 0.28(B-V)₀ + 0.04 E_B-V

　　　r = 10^{(V - Mv + 5 -Av)/5}

　Mv, (B-V)₀, R 式は Schmidt-Kaler 1982 から採った。

　区分分け　

　天空は Lucke (1978) の近傍赤化分布図にしたがって、199 の細胞に分割された。 Neckel, Klare (1980) の図は Av は第一近似として二次式で表されることを示す。各細胞で Av は次の式で表されるとする。

　　　Av = α r + β r² (r < r_o)

ここに r_o = 吸収層境界までの距離である。r_o の第１近似は

　　　r_o = 0.2 kpc/sin b

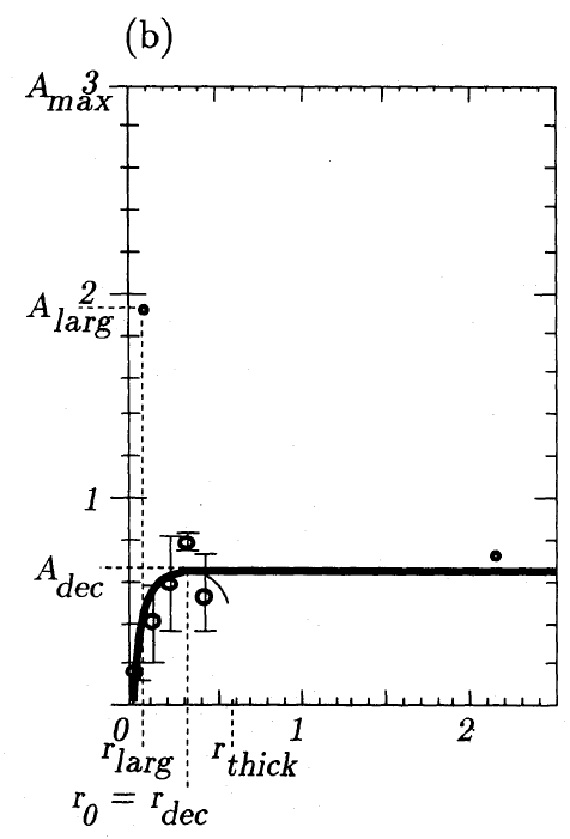
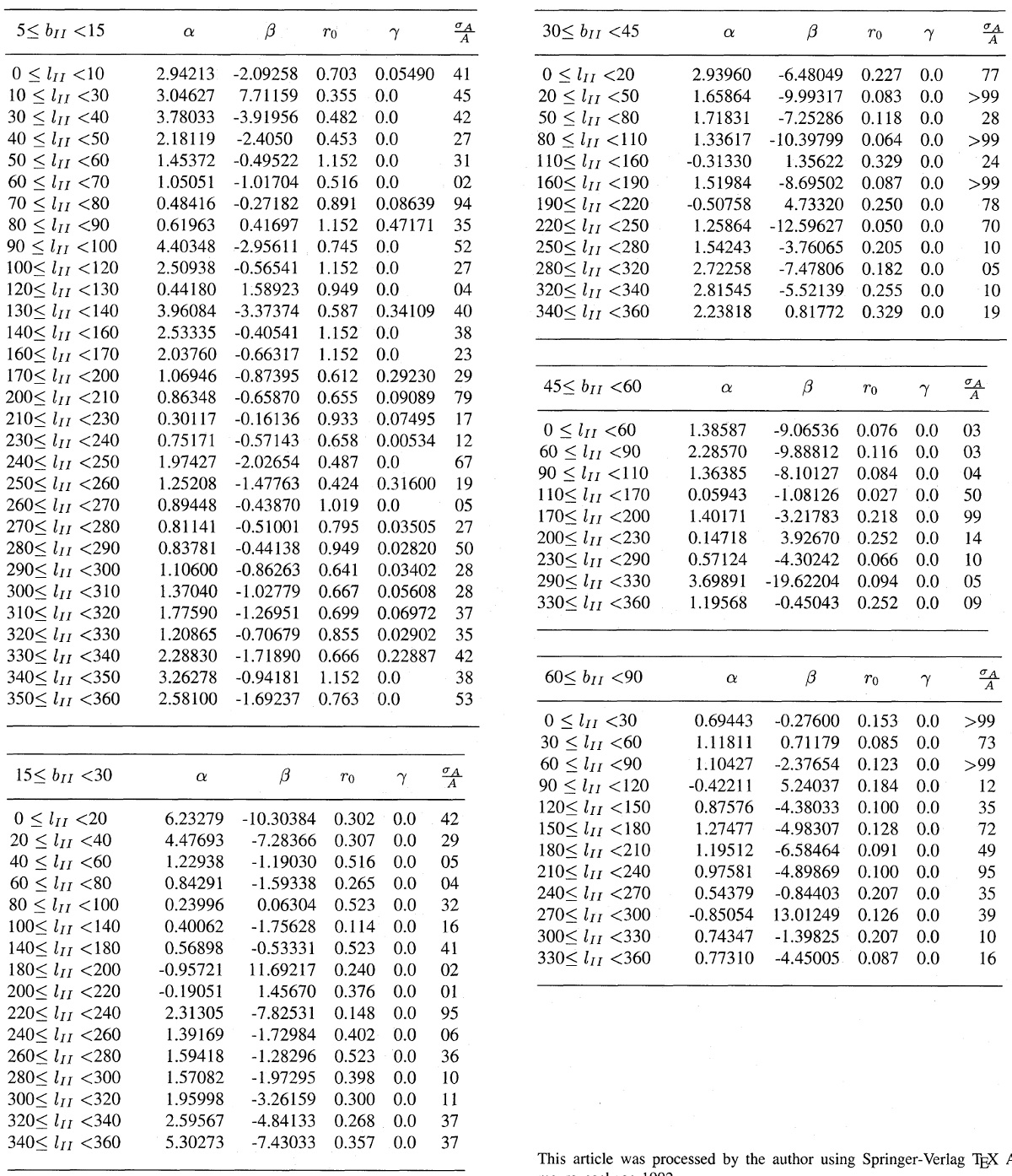
図１b．l = [20, 40], b = [15, 30] の Av-D 関係。ビン＝ 100 pc.

　r_o の先は？　

　中間ー高銀緯では r_o の先吸収は一定である。低銀緯 |b| < 15° ではその先線形の伸びを加算する。

　　　Av = Av(r_o) + γ (r-r_o)

　r_dec と r_larg　

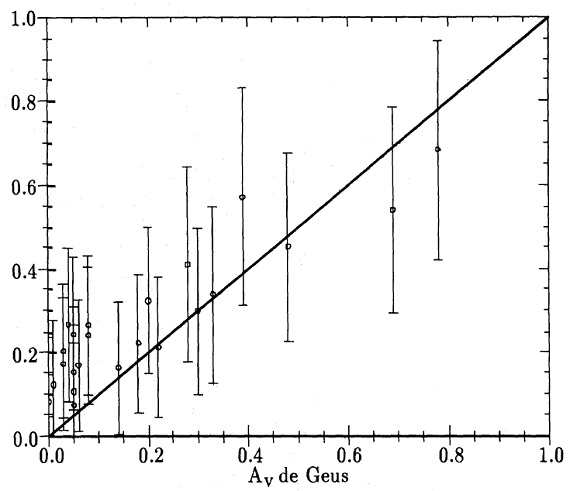
　上の図１を眺めると Av は r = r_dec で放物線の頂点に達する。その先 Av は下降するがそれは近似式の人工効果である。また、一方　Av はその方向で観測されるされる最大値、その時の距離 r を r_larg とする、を超えてはいけない。その上、この最大減光値は文献に見られる結果と比較されるべきである。我々は以下の値を採用する：

　　　A_max = 0.1 (60° ≤ |b| ≤ 90°)

　　　A_max = 1.2 (45° ≤ |b| ≤ 60°)

　　　A_max = 3.0 (45° ≤ |b|)

A_max に対応する距離 r_max は図１には現れない。なぜならそれは図１a では 9 kpc であり、図１b では到達しない値だからである。

　Av 誤差　

　各星に対し、Av の誤差を以下の式で与える：

　　　err_Av = { 0.15² + [σ_Av/Av)Av(r)]²}^1/2

ここに、0.15 mag は最初の３つの公式から Av を導く際の不定性の仮定値である。相対誤差 σ_Av/Av の全天平均は約 35 % である。

　r ≤ 200 pc で Av 大きめ　

　全天の一般的な減光パターンを求めたため、減光物質の細かい不規則性は無視されている。r ≤ 200 pc では Av を少し大きめに表す傾向がある。図２に de Geus et al 1989 による Walraven 測光からの結果を比較したが、それを見ても分かる。

　Neckel, Klare 1980　

Av < 0.5 では Neckel, Klare (1980) との一致は非常に良い。Av 大の所では物質分布の細かい不規則性が効いてくる。

図２．我々の Av と de Geus et al 1989 の　Av のケンタウルス-狼座上部領域での比較 　

　４．(B-V) の評価　

表３．MK-スペクトル型の与えられた星について（B-V) への補正と (B-V) の不定性。

　δ_B-V 　

　表１、２にある各星に対し、前節で与えられる Av を用いて (B-V) を計算した。それを (B-V)_red と名付ける。 δ_B-V = (B-V)_red - (B-V)_ph の分布を, スペクトル型、光度クラス別に計算した。表３と４には E_B-V の４区分における ⟨δ⟩ を示す。 ⟨δ⟩ はゼロに近いと期待されるが、一般には E_B-V と共に増加して行く。
( δ_B-V = (B-V)_red - (B-V)₀ じゃないのか？ )

　Ｂ－Ｖ　

　スペクトル型から Mv, (B-V)o が分かる星の V が与えられたとする。逐次近似のスタートとして Av = 0 を仮定する。そこから Av(r) を決め、 (B-V) = (B-V)o + E(B-V) - δ_B-V を得る。
( 何をしているか理解できない )

表４．HD-スペクトル型の与えられた星について（B-V) への補正と (B-V) の不定性。

　５．暫定データをヒッパルコススターマッパーと比較　

図３a．MK スペクトル型星に対する Δ(B-V) = (B-V)_NDAC - (B-V)_INCA とスペクトル型の分布。

　カラー比較　

　上に述べたモデルは内部無矛盾であるが、INCA チームが予想した (B-V)_INCA と NDAC 整約チームの予備観測から求められたカラーを比較することは有意味である。

　Δ(B-V) 　

　図３に Δ(B-V) = (B-V)_NDAC - (B-V)_INCA の分布を示す。