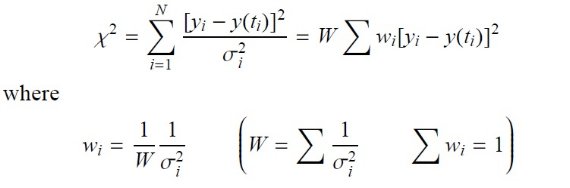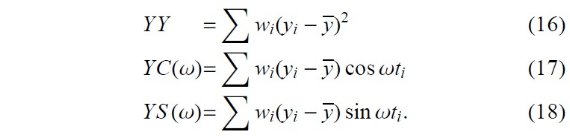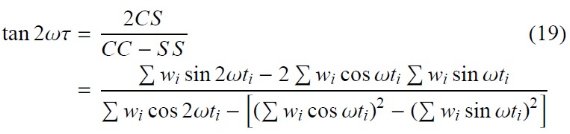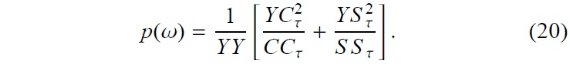The Generalized Lomb-Scargle Periodgram: A New Formalism for the Floating-Mean and Keplerian Periodgram


Zechmeister, Kurster
2009 AA ???, ???



　アブストラクト　

　ロム・スカーグルのピリオドグラムは非一様間隔のデータの周期解析において、 サイン波の最少二乗フィットと同等な方法である。我々は、これを完全サイン波 フィットに拡張し、オフセット、重みも含むようにした。ロム・スカーグルの ピリオドグラムと比較すると、周波数精度が上がり、偽信号に強く、スペクトル 密度がよく決まる。計算上の修正は僅かで、計算時間も同じくらいである。 我々の方法は、いくつかの方法、date-compensated discrete フーリエ変換、 浮動平均ピリオドグラム、SiigSpec プログラム中で用いられるスペクトル重要性 などを合わせている。 　そのうえ、我々は視線速度データにケプラー運動のベストフィット周期を求 めるためのケプラリアンピリオドグラムを評価するために、この一般化された 方法を補足するアルゴリズムも示す。系統的で、非ランダムなアルゴリズムは 離心率軌道を検出することが出来る。それを二つの例で示す。それは系外惑星 の周期を探すのに有用な武器となるであろう。

　１．イントロダクション　

　ロム・スカーグルのピリオドグラム　

　ロム・スカーグルのピリオドグラムは時系列の周波数解析に広く使われてい る。これは

　　　y = a cosωt + b sinωt

をフィットすることと同等である。標準的な解法では各サンプル周波数毎に 連立線形方程式を解く必要がある。ロム・スカーグル法はそれに簡便で効率的 な解析解を提供する。 　サンプル平均がゼロの時系列を (ti, yi) (⟨y⟩=0) とする。ロム・スカーグルのピリオドグラムは以下で定義 される。



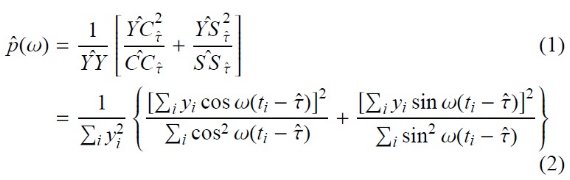
ここでハットは通常の意味である。パラメタ― τ^ は次の式で定義される。

　ロム・スカーグルのピリオドグラムの欠点　

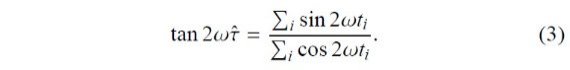
　しかし、この方法には二つの欠陥がある。

（１）ロム・スカーグルのピリオドグラム法は測定誤差を考慮していない。

（２）解析では、サンプル平均をデータから引いて、平均をゼロにする。

（１）は重み付き和を導入することで解決する。これは χ2 法の 一般化と同等である。（２）はサンプル平均とフィット解の平均が一致すると いう前提があるが、これは正しくない。これはオフセット c の導入を必要とする。 全体としては、

　　　y = a cosωt + b sinωt + c

を重み付きフィットすることに等しい。

　前史　

　基本的にはオフセット項を含む全サイン関数の最少二乗スペクトル は Ferraz-Mello 1981 が与えていた。彼はこの方法を date-compensated discrete Fourier transform (DCDFT) と呼んだ。 我々は表記をロム・スカーグルのピリオドグラム法と同じにして、 一般化したロム・スカーグルのピリオドグラム法と呼びたい。

　２．一般化したロム・スカーグルのピリオドグラム法　

　計算式　

　時系列データセットを (ti, yi, σi) とする。このデータを与えられた角振動数 ω （周期 P = 2π/ω） で全サイン（定数項を含む）関数

　　　y = a cosωt + b sinωt + c

でフィットすることを考える。これは以下の χ2 を最小に することである。



ここに、wi は規格化された重みである。 χ2 の 最小化は３元連立線型方程式に導き、その解は付録Ａに記した。

p(ω) = 相対的 χ2 reduction　　

　p(ω) = 相対的 χ2 reduction は１に規格化され、以下で 与えられる。



　　　χ02 = W・YY　である。

　式 (10) - (12) は以下のようにも書ける。



　式 (4) は 1 に規格化されている。0 ≤ p ≤ 1 であり、 p = 0 は全く 合っていない、 p = 1 は完全なフィット(χ2=0) を意味する。

　時間原点　

　全サイン関数フィットは時間に対して変換不変なので、任意の時間原点 τ を導入して、tj &rarrow; tj - τ としても χ2 の値は変わらない。そこで、τ を以下のように取る。



すると CS = 0 となり、式 (5) は以下のようになる。



注意したいのは式 (20) は式 (1) と形式的に同じ形である。

　実際の計算では　

　計算の手間はロム・スカーグルのピリオドグラム法と同じくらいである。もし、 式 20 を使うのを止めて、式（５）で CS をそのまま保って計算を行うなら、計算 の手間はさらに少なくなる。

　３．規格化と　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．


( )


et al. () 先頭へ