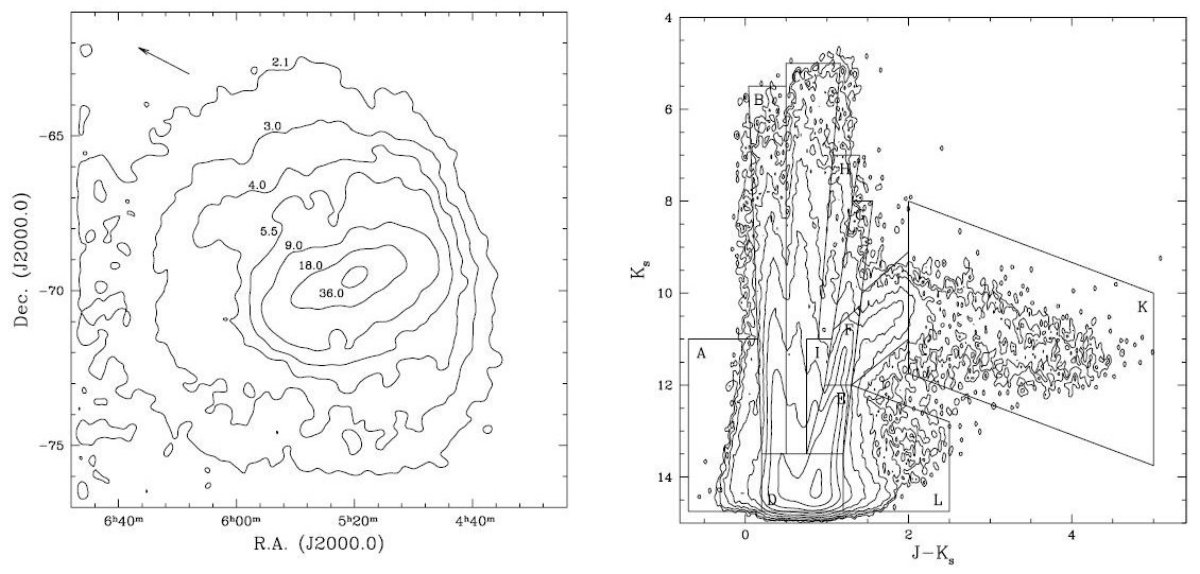
アブストラクトLMC の 2MASS データを用い、標準光源解析とスターカウントからLMC の構造 パラメターと広がった潮汐デブリの証拠を導いた。若いのと古い種族のスターカウント と投影還元した傾斜角は以前の研究と一致した。投影密度を指数関数型円盤または 球対称冪乗則モデルに2次元楕円バーを加えたモデルでフィットした。得られた 円盤スケール長はバーなしモデルで R = 1.42 ±0.01 kpc, バーありで R = 2.15 ±0.01 kpc であった。バーの軸比は中間年齢と高齢種族に対し q = 3.4, 若い 種族に対し q= 4.1 であった。星密度の動径分布は円盤が半径 3 kpc で途切れることを 示す。全領域を覆うデータと大きな (LMC 直径/銀河系中心距離)を用いて、 (何のことか意味不明。) |
円盤の傾斜角を求めた。その値は
星種族により異なり、 i = 22° - 29° であり、平均は i = 24.0°
±0.3° である。バーを含むモデルから導かれた傾斜角はもっと大きく、
i = 38.2° ±0.4° である。 1.6 < (J-Ks) < 1.7 の炭素星長周期変光星を用いた標準光源解析は LMC の 3次元構造を明らかにした。選択領域内の炭素星長周期変光星の固有光度分布は、この カラー領域内で σM ≤ 0.2 mag であることを示す。このサンプル は LMC 円盤傾斜角の直接決定値として i = 42.3° ±7.2° を与える。 等級分布の著しい特徴からいくつかの種族が区別された。我々はそれらを LMC の 広がった厚さ 8 kpc の恒星成分、と LMC から 14 kpc 離れた潮汐デブリと考えた。 別のモデルとして、この特徴は AGB 進化に現れるものでさらなる理論的研究を 促すものかも知れない。 |
|
円盤の形と運動: これまでの話 LMC = Irregular Barred Spiral (de Vauvouleurs and Freeman 1972) Inclination=27°(de Vauvouleurs 1958, 1980) 投影形、測光から 回転 プローブ天体は、 1. HI 2. PN 3. HIIR 4. 超巨星 5. CH星 −−> 回転中心 (5h21m, -69°17')1950 バー光学中心 から0.6° 北 星団の運動 若い星団はHIと同じ運動 Freeman etal 1983 SWB VII の古い星団は、視線速度の分散σ=18km/sで平たい回転系 さらに外側の星団の運動 圧力保持的な楕円体はない。 Schommer 1990 ――> LMCは幾何学的に薄い円盤 円盤の形と運動: 最近の話 (1)古い変光星の運動は回転楕円体 Hughs,Wood,Reid 1991 (2)炭素星が12kpc離れて存在。 |
(3)銀河系の潮汐力によるLMC回転軸歳差運動 Weinberg 2000 円盤面外へのトルクを生じ、LMC 外縁に強くフレアした回転楕円体的 な質量分布と星とガスの放出を生む。この効果は運動額的には小さい σ のように円盤の特長を保持したまま形は広がった成分を作る。 この論文の目的と結果 上の広がった成分を検出すること。 Nikolaev/Weinberg 2000 から CMD の各星成分ごとに分布を調べる。 低温巨星を使った結果は、傾斜角 = 22° - 29°、方位角 = 168° - 173° CMD の J 領域、1.6 <J-K < 1.7 は良い標準光源になる。 その光度分布を見ると3つのピークがある。 細いピークは円盤のもの。 他の2つの副ピークの微分測光距離を調べ、I = 42.3° ±7.2° これは、様々な要因のからまった結果である。 しかし、とにかく厚みは 8 kpc で、Hughs etal 1991 が示唆した回転楕円体の 2.8 kpc より厚い。 |

|
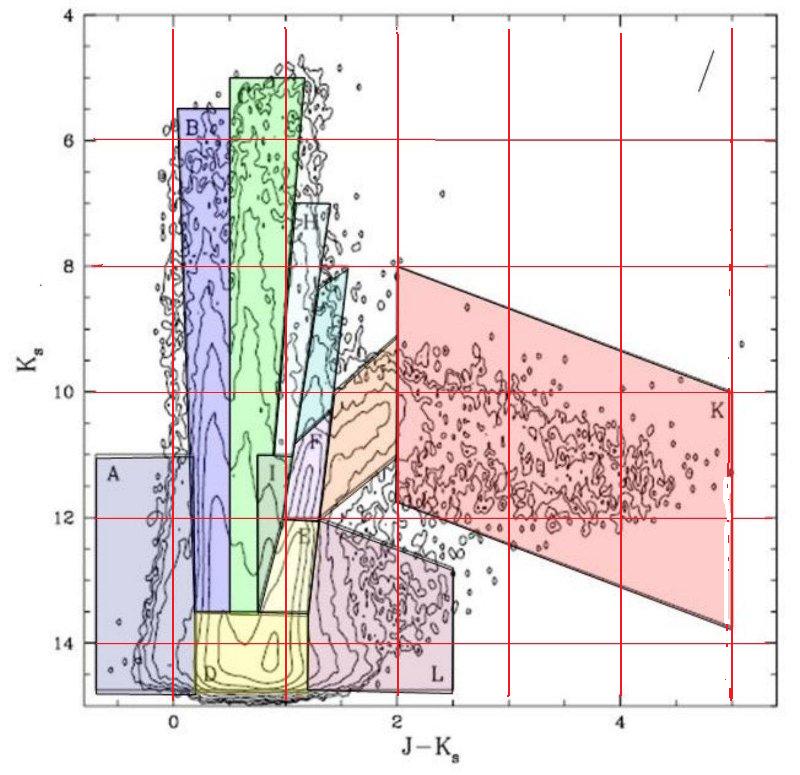
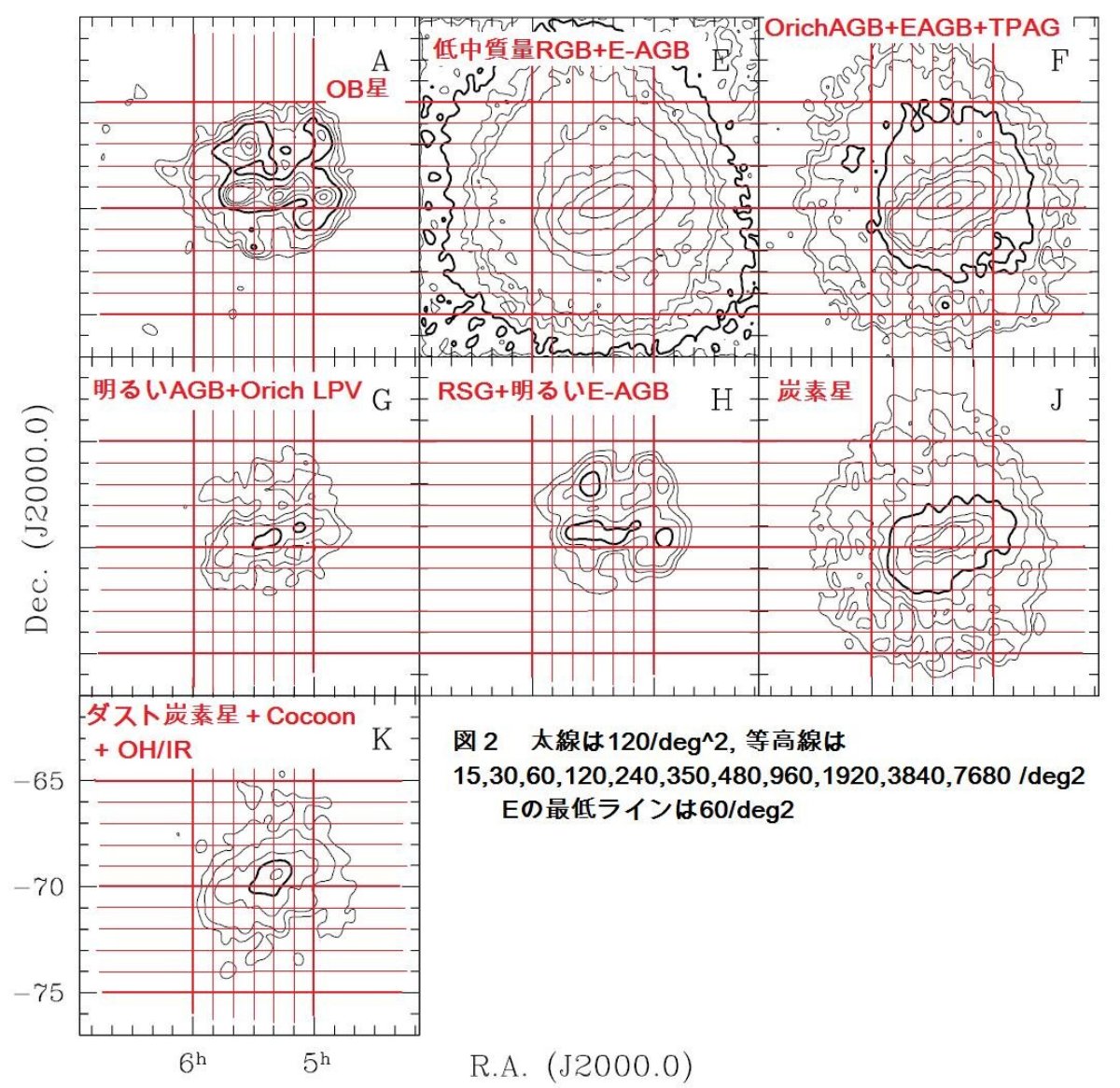
CMD 上の分類 A: O,B,A超巨星、O3−O6矮星 B: 銀河系F-K矮星、LMC超巨星 C: 銀河系K矮星とK巨星、LMCバー超巨星 D: 左角=銀河系G-M矮星、右角=LMCのRGB,E-AGB星 E: 低―中間質量星RGB、E-AGB星 F: O-rich AGB星、E-AGB星、TP-AGB星 G: 明るいAGB星、O-rich LPV H: RSG、明るいE-AGB星 I: J: C-rich TP-AGB星 K: Dusty C-rich TP-AGB、Cocoon星、OH/IR L: |
 |
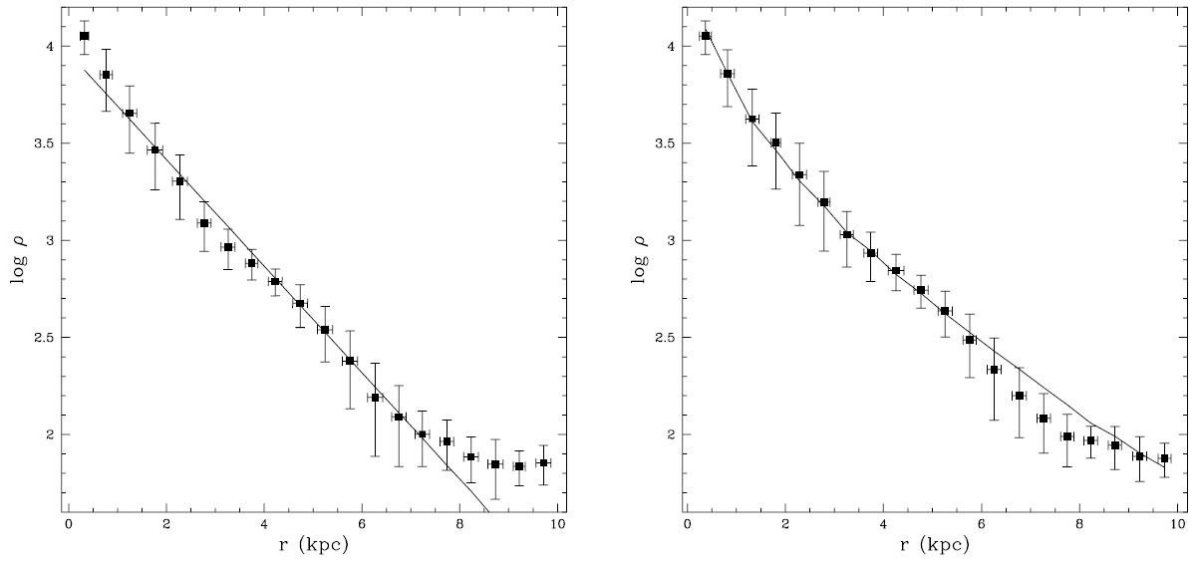
モデル  のパラメター9個をビンの中の星の数でフィットする。 7つは共通で、 LMC中心 (αo, δo) (J2000) インクリネーション i 位置角(position angle) θ (中心からの方向を北極方向=0とし、反時計回りに測る) バーの方位角(azimuthal angle) φ (北から時計回り) バーのスケール a バーの形 q 残りの2つは(ρD、b)または(ρS、ν)である。 | フィッティングの方法 N×M個の小領域の観測星数 noij とモデル星数 neij から 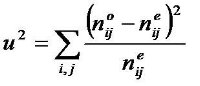 この u2 は goodness-of-fit measure と呼ばれ、自由度(N×M−1− np) のχ2 分布。 np はパラメター数。結果は下の表のようであった。 星のグループ毎に異なる結果が得られた。 (1) A,H(若い星)(2) E,F,J,K(古い星)(3) G 特別 χ2/dofが大きいのは非軸対称成分が大きいためであろう。そこで非軸対称成分 を入れれば他のパラメターをそう変えずにχを下げると考えて、相対値を問題に することにする。 若い星 フィットは悪い。むらむらが大きいため?スケール長も他より大きいし中心もバー の光学中心(α=80.9°δ=-69.8°)2000 の1°北になる。 バーなしモデルで決めたi=35°は、 38.2° HI分布から Feitzinger et al 1977 36° モンテカルロでLMC西側のUV偏光マップをフィット Cole et al 1999 と矛盾しない。 古い星 スムーズな分布で、スケール長平均値R=1.42kpc(バーなし)、2.15 kpc (バーあり)は1.46kpc Bothun/Thompson 1988 とも合う。 Eの星はR=1.58kpcで他の古い星より有意に大きい。MACHOでRRLyrからのR=1.6kpc と合う。 図4にあるように前景の銀河系M矮星の影響がある。他の古い星グループはr=3kpc で切れている。 |
|
古い星のインクリネーションは平均i=24°で 25° 星カウント de Vaucouleurs 1955 25° 星団分布 25° HI等高線 McGee/Milton 1966 27° Rバンド写真 de Vaucouleurs 1957 と良く合う。 古い星のバー付きモデルでは15°増えてi=38° Cepheid:Laney/Stobie1986 45°Welch 1987 37° 位置角はθ=168―173°で他の値と合う。Schmidt-Kaler/Gochemann 1992 バーモデルの位置角は12−17度である。 表3を見ると、inclination=-38°〜-41°で上の符号が逆。大体inclinationが負は 何を意味するか? 確かに、平面の傾きをi とθで一意に表せるのかよく判らない。ここで言う位置角は nodeの向きではないのかも知れない? | 2MASSのカバー領域が広いので傾きの絶対的な方向、つまりLMCのどちらが近い側か を決められる。 銀河系のコンタミを避けるためにJを使う。 つまりこれまではどっちが近い側は決めないで話をしていたらしい。 表3に球対称分布に対する結果、バーなしで全グループν=2.5、を示す。別の話に飛 んだ? Hughs(1991)の中間年齢・古いLPVを使ったモデルと比較する。 Hughs Ours OldLPV IntermediateLPV E,F,G,J 数 63 81 200,000 R 1.6kpc 1.7kpc 1.4kpc ν 1.8 1.7 2.5 Rcutは同じだが、νは差がある。周辺部で多いためだろう。逆センスに思える。 まとめると、2MASSのLMC投影分布は以前の結果と一致する。 スケール長 R = 1.4kpc、インクリネーション=22−24°、チルトの方向(?) も矛盾しない。 |
4.1.選択領域JはRGBチップより明るく、充分な数があり、光度の分散が小さい。O-richLPVはほとんどJ-Ks<1.5なので(Hughs,Wood1990)、JはTP-AGBの炭素星ミラ、 SRである。 Pデータがないので、PLRやPLCRは使えない。光度―カラー関係を使う。問題はSRa星 に同じL-C関係が使えるか?チェックのため、Hughs,Wood1990サンプルからJ−Ks<2 のミラとSraを選んで別々にフィットした。 Ks=-0.96(J-Ks)+12.52 ミラ Ks=-0.90(J-Ks)+12.24 Sra で差はない。 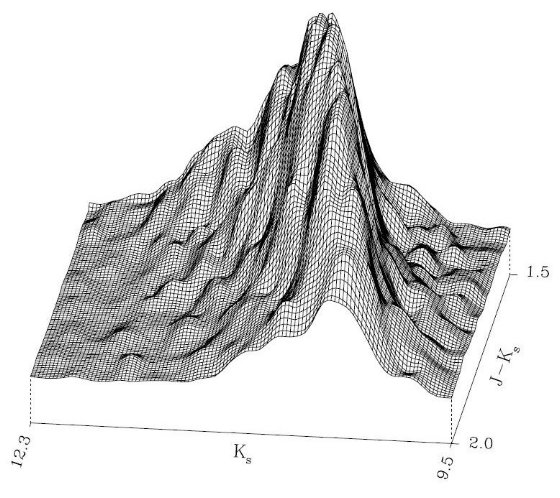 図6.CMD J 領域の密度マップ。J-Ks = 1.5 - 2.0 である。はっきりしたリッジ は J 領域星のカラー対光度関係が良く定義されていることを示す。 | これはC系列の話で、B系列には多数のSRが含まれている。影響は4.3.2 で。 J領域には8229星が含まれる。 Glass(1990)の79ミラ観測結果から図5の点線ではさまれた, 1.4 < J-Ks < 1.9 の14Cミラに対して、 Ks=-0.99(J-Ks)+12.36 今回は1.6<J−Ks<1.7の範囲の星を使う。これでLの範囲は小さくなる。 2MASSは一回観測なので変光位相による分散がかかる。ミラはGlassによるとΔK<0.5 だが、大部分はSRなのでΔKはもっと小さい、実際CMDでJ領域の枝はσ〜0.2. 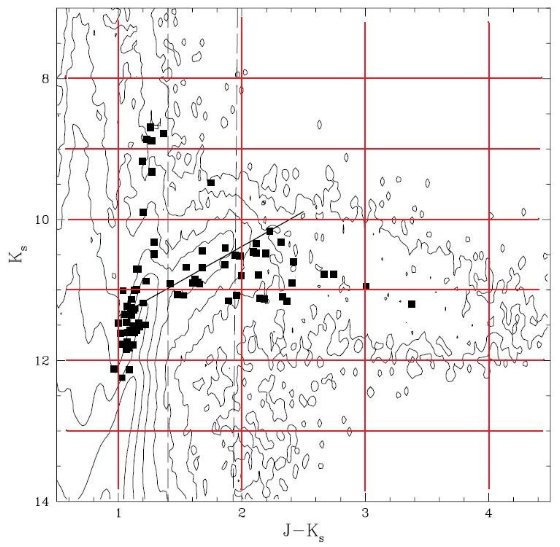 図7.Glass 1990 から選択した 79 ミラ(C-, M-) のプロット。縦の破線は 選択カラー範囲 1.4 < J-Ks < 1.9 を示す。実線はフィットしたカラー対 光度関係。 |
4.2 方法円盤の傾きによる距離のずれが無視できる程度に小さい領域で光度分布のセント ロイドを決める。領域はNODEおよび直行する大円に沿って並ぶ。⟨m⟩ = セントロイド 2σm=見かけ等級の分布の巾 σm2=σM2+(4.72/RLMC 2)σr2+σA2 +σph2 RLMC =50kpc, σM =絶対等級の分散、 σA=減光の分散, σr=円盤厚み、 |
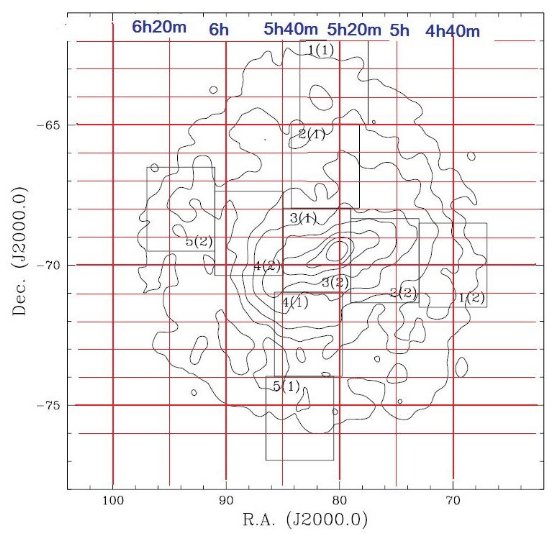 図8.選択した LMC フィールド位置。Arc1 = N-S 方向。ノード線に平行。 Arc2 = E - W 方向。ノード線に直交。数字はフィールド番号。 |
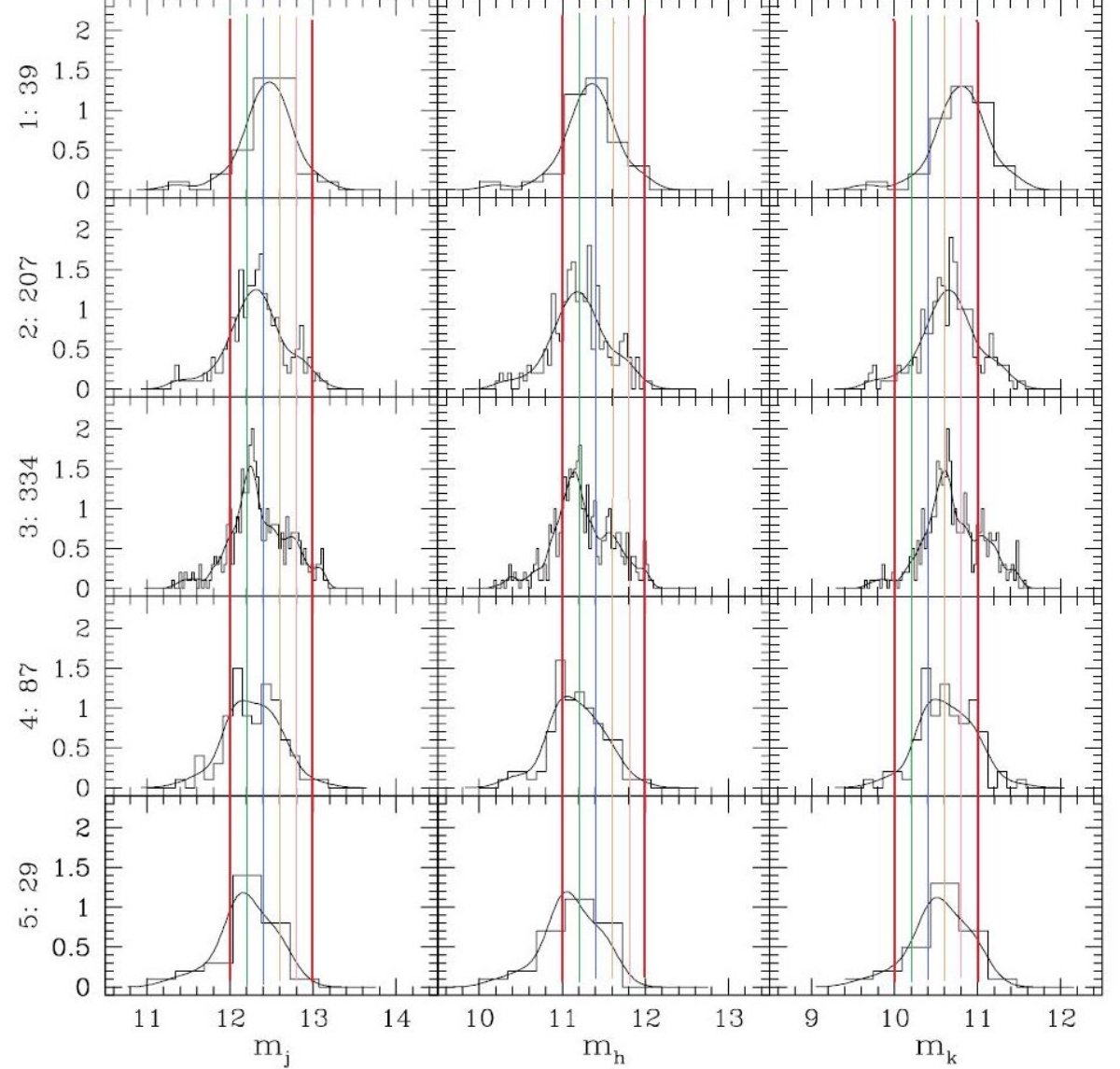
4.3 結果。3.1.セントロイド3章とは独立に円盤の傾きを決める。 方法1 南北線と東西線の傾きを求める。 南北=42.3°東西=0.9° 方法2 領域3(中心)と各点との傾きを決め、その 重みつき平均をとる。 南北=34.4°、東西=1.0° 減光の効果はどうか Oestreicher/Schmidt-Kaler 1996の減光マップにその傾向は見られない。 NW00のRGB位置の解析でも中心1平方度の外で減光小 | 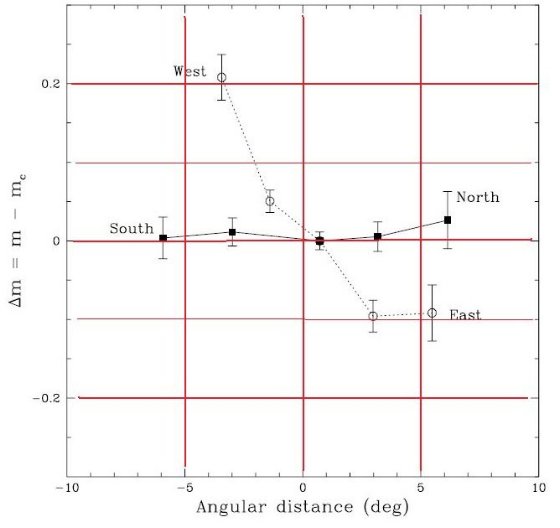 図11.J,H,Ks の平均等級のオフセット値をバー光学中心からの距離の 関数としてプロット。 |
|
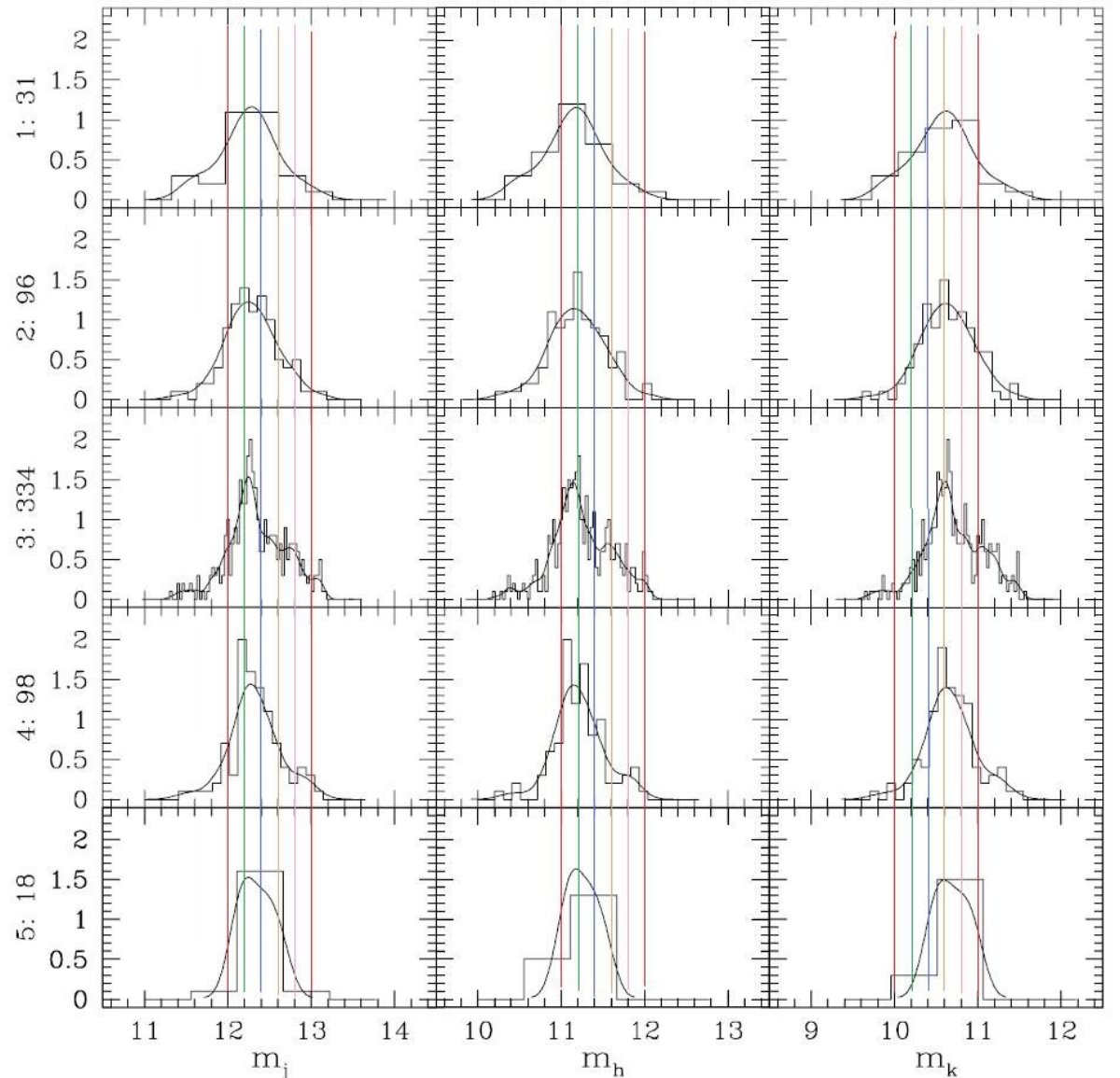
4.3.2. 等級分布の形 図9,10の分布曲線にはテールが見える。東西線に沿う5領域の1719星J,H,Kを、 多分ピークを合わせることで、一つの分布にまとめ、ガウスの重ね合わせで近似した。 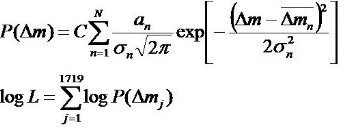 ガウス成分が一つ増えるとパラメターは3増える。 3成分と1成分の差はΔlogL=52で、 Statistical significanceで 1-exp(−104/6)=1なので、3成分モデルがよい。 3と4ではΔlogL=4で、 Statistical significance=0.93で弱い。 ガウス成分の数はAICで決められるんじゃないか? AIC=-2lnL+2Kが最小を選ぶ。K=パラメター数 ガウス数 ΔlnL K ΔAIC 1 0 3 6 2 39.8 6 -28 3 52.3 18 -68 4 56.3 24 -64 3成分がよい。WNも同じ結論に達した。 | 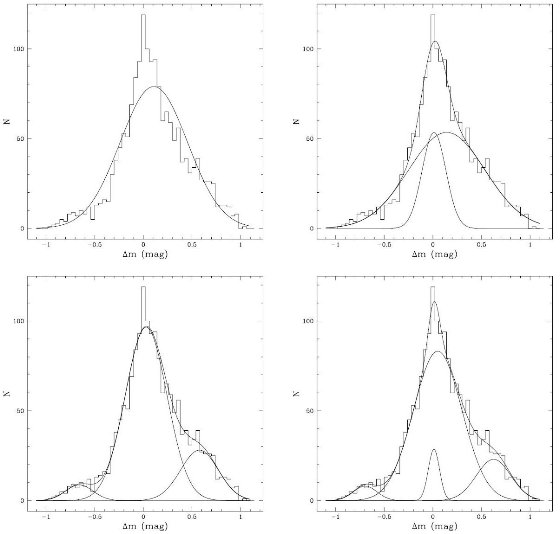 図12.見かけ光度関数のガウシアン解析 |
|
3成分の解釈 中央ピークはLMC円盤。 75% 第二ピークは0.6等暗い。 20% 第三ピークは0.7等明るい 5% 減光はバンド毎に異なるテールを生むはずなのに同じ大きさのテールだから否定。 銀河系はJ領域にはほとんどない筈なので否定。残る可能性を以下に検討する。 1.ブレンド 第二ピークが明るいほうに出るはずなので否定。 2.オーバートーン振動 Hughs/Wood1990の基本振動のミラを調べた。J-Ks<2の91星のKsをL-C関係に沿っ てずらし、1.6<J-Ks<1.7に移した。 2グループをKSで調べたが、P=0.257なので「2グループが同じ母集団」という 帰無仮説を棄却できない。 実際、実線(基本振動ミラ)にもやはり0.6等暗いところに第二ピークがある。 3.周期分布 周期に分散があるかもしれない。 4.年齢―メタル変化 Marigo,Bresson,Chiosi1996 同じPでもAGBマスが違うとLが変わる。 Cole2000(Private communication) LFをMarigo etalの進化パスに合わせると 強いピーク=0.6Gyr (2Mo) 暗いピーク=2.8Gyr (1.2Mo) Frogel,Mould,Blanco1990 t=100Myr〜3Gyrの星団に炭素星が存在。若い炭素星は 明るい。 Alves et al 1998 NGC1783(中間年齢)の炭素星は同じ周期でNGC1898(古い) の炭素星より0.5等明るい。 しかし、 (1)明るい第二ピークが説明できない。 (2)2.8Gyr前のバーストに続く星形成率が小さくないとピークにならない。 ので、否定する。 5.星の進化 サーマルパルスで明るく、暗くなる可能性はある。 6.広がった分布 LMC中心から14kpcはなれた塊り。LPVを含むから割と若い。 Graff et al 2000 炭素星のVr分布から Zaritsky/Lin 1997 中間の星種族 Hughs et al 2001 広がった楕円体成分 成分の厚みσrはσMの取り方による。σr=1.5kpc(σM=0.2) σr=4.3kpc(σM=0.1) L-C関係では誤差が大きい。完全なP-L-C関係を用いた精度の高い研究でLMCの 厚みを出す必要がある。 |
 図13 Hughs/Wood1990からの91基本振動ミラ(L-C関係でずらした)と 2MASS1719星のKs分布。 |