
| 渦状腕のピッチ角は何度だろうか?銀河系にある渦状腕の数は幾つだろうか? 派生(羽状)腕モデルは古典的な対数腕より良いのか悪いのかどっちだろう? グランドデザインの2本腕と4本腕の選択は? | 統計的解析を用いた新しい解析法を観測データに適用して、過去に8個の方 法で決められたピッチ角の問題を扱った。銀河系に似た系外銀河との比較を 行い、また対数腕と羽状腕の比較を二本腕で行った。磁場を取り入れたのは この論文が最初である。過去 15 年間のデータから p = -12°±1 °, m - 4 で、対数腕の方が羽状腕より優れているという結果を得た。 |
| Elmegreen は 1985 年のレビューで、「全てのモデルは観測と大体合っている。 より多くの観測が、腕の数、ピッチ角、対称性の決定に必要である。」と述べた。 その後20年経ち、再びこの疑問に戻る時期が来た。 | その後の新しい観測データをこの観点から検討する。 |

2.1.データ1980 年代以降の渦状腕の追跡は、主に可視及び電波 HIIR により行われた。 また最近の観測は磁力線が渦状腕に平行に平行であり、したがって磁力線の 位置と方向は渦状腕の研究に使えることを示唆する。表1には 1980 年以降の 関連研究を載せた。ピッチ角に関する収斂傾向は見られない。それを図1に 示す。2.2.評価個々の研究を手法で分けた:(1)パルサーのRMから決めた磁場の方向 パルサーのファラディ-回転(RM)をモデル予想と比較。重み=2. (2)クウェーサーと銀河の RM から決める磁場の方向 これも重み=2 (3)ダストの分布 可視減光は太陽近傍の情報を与えるが遠方の構造に関して不足。重み=1 (4)分子雲の分布。 運動距離の不定性と言う弱点が近年克服されつつある。重み=2. (5)HI ガス これも運動距離という弱点がある。おもみ=2. (6)熱電子 パルサーディスパージョンメジャーを用いた自由熱電子も運動モデル を必要とする。重み=2 |
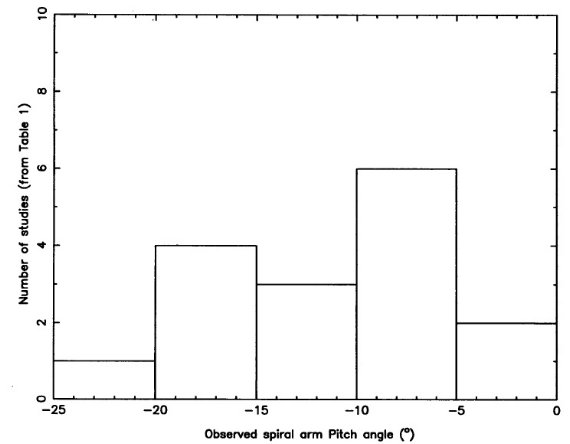 図1.表1からの個々の研究で得られたピッチ角のヒストグラム (7)HIIRs 可視光と電波を用いた研究では、測光距離と運動距離の両方が用いられる。 重み=3. (8)星とアソシエイション 測光距離を用いる。重み=2. |

|
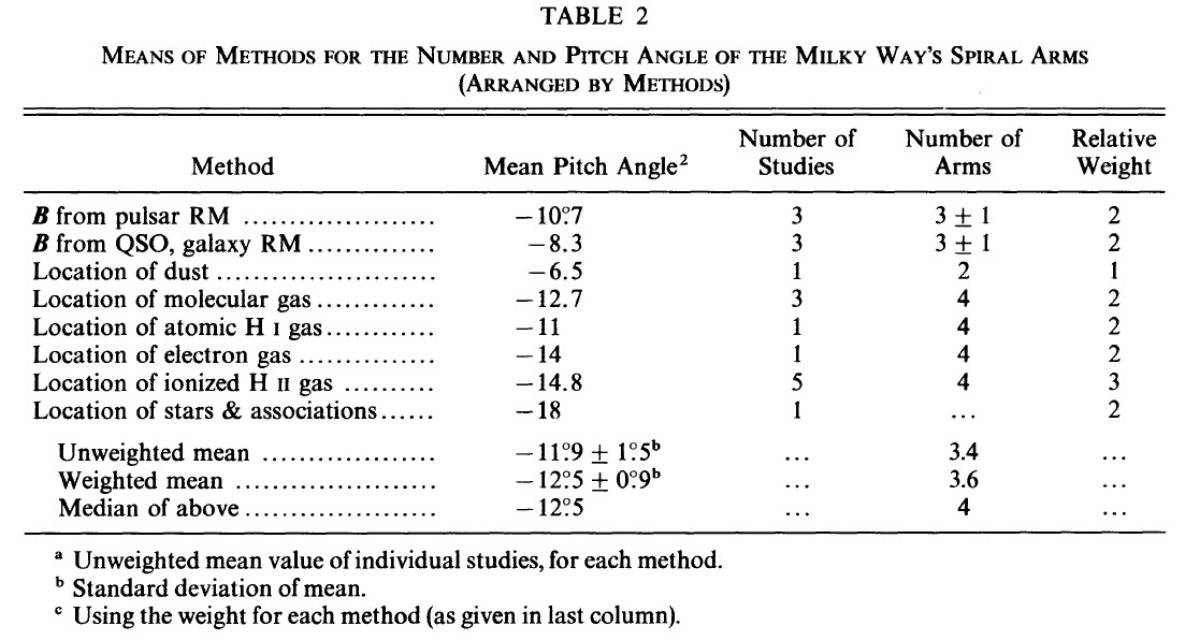
手法毎のピッチ角と腕数の平均 表2には各手法でのピッチ角と腕数の平均値、更に手法間の重み無し 平均と、重みありでの平均を載せた。 平均ピッチ角の分布 図2には、手法毎の平均ピッチ角のヒストグラムを示す。 ([-15,-10] 区間には5個のはず?。 ) |
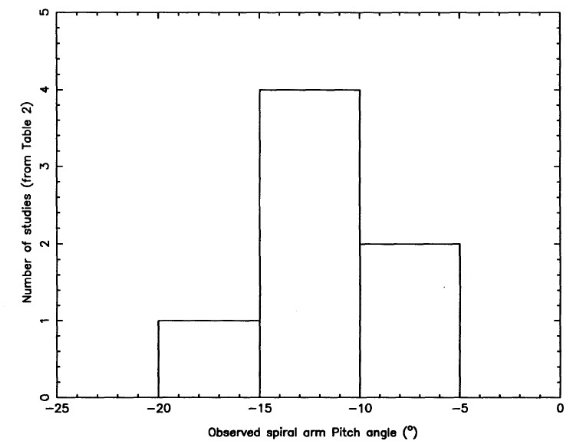 図2.あるピッチ角を与える方法数のヒストグラム。図1に比べ、ピッチ角の 分布巾が狭くなっていることが判る。ピークは [-10, -15] にある。 |
3.1.ピッチ角の巾Kennicutt 1981 は銀河タイプとピッチ角の間の関係を調べた。銀河系は Sbc 型らしい。このタイプではピッチ角は最低 -11° で中間値 -14°, 最大 -28° である。 すると、ピッチ角 [-10,0] の研究はありそうにない。(銀河系のタイプに問題?。 ) |
3.2.グランドデザイン、多重腕?AC分類Elmegreen,Elmegreen 1982 は渦状銀河の 69 % は二本の長い腕 を持ちグランドデザイン銀河と名付けられる。 31 % は多数の短い 腕片を非対称に分布させ、羽状銀河と名付けられる。Elmegreen,Elmegreen 1987 は 762 渦状銀河を AC1 - AC12 に分類した。AC1 - AC3 は極端羽状で、 AC11-AC12 は極端グランドデザインである。 銀河系には数本の目立って大きな腕がある。特にサジタリウス腕は |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
