Udalski98c

OGLE: Short Distance Scale to the LMC

Udalski,A., Pietrzynski + 4

1998 ApJ 509, L25 - L28

　アブストラクト
赤化の評価　

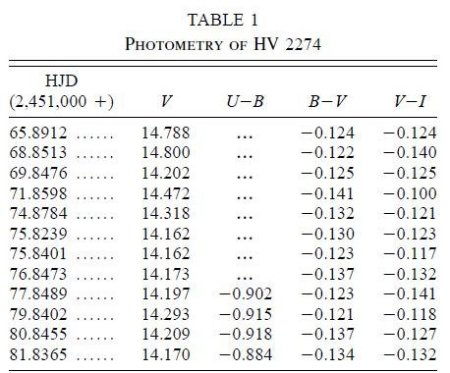
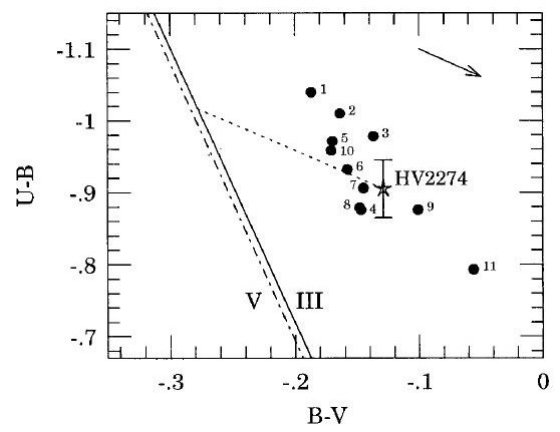
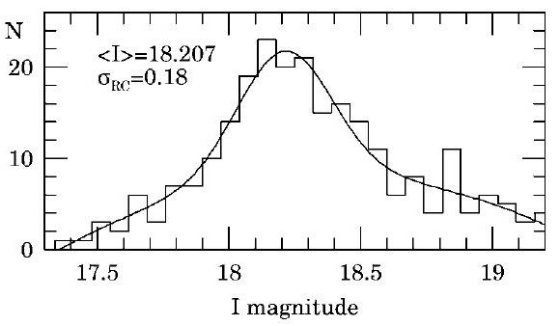
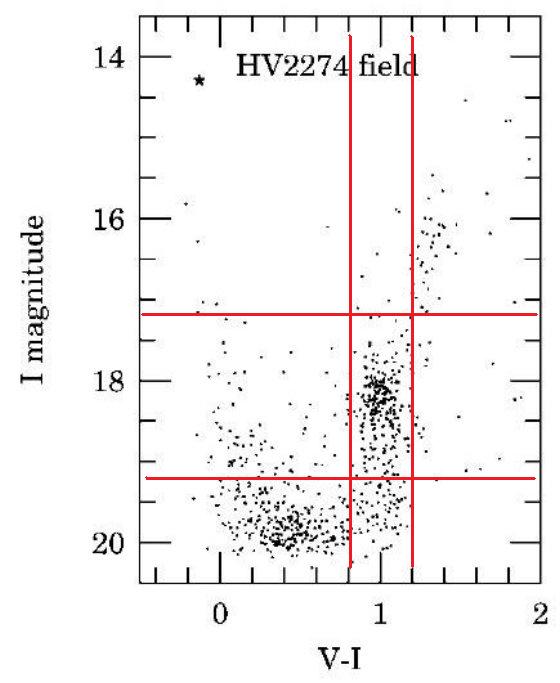
　LMC 内の食連星 HV 2274 の UBVI 測光を報告する。この星は Guinan et al 1998 により LMC への距離決定に用いられた。カラーの観測値から、この星への赤化を E(B-V) = 0.149 ± 0.015 と定めた。この値は周辺のレッドクランプ星の観測から求めた局所平均赤化の値と良い一致を示す。この赤化の値は Guinan et al が使用した値のほぼ２倍である。

赤化の影響　

　赤化を修正すると、見かけ等級が明るくなり、距離を小さくする効果がある。その結果 LMC に対し、 m - M = 18.22 ±0.13 となった。これは LMC の短距離説を支持する結果である。これは最近の RR Lyr, レッドクランプから求めた LMC 距離の結果と一致する。
　1.イントロ　
LMC 距離論争

　セファイドによる LMC 距離は系外天体への距離に結び付けられている Kennicutt, Freedman, Mould 1995 。これは Laney, Stobie 1994 による仕事だ。この標準値に反する短距離は、 RR Lyr やレッドクランプ星(18.18±0.06)から得られている。レッドクランプ星のみがヒッパルコスによる三角視差による較正を経ていることを強調しておきたい。

連星視差

　LMC 距離の論争に決着をつける新しい方法と期待されているのが食連星法である。 Paczynski 1997 はこの方法を最も有望と考えている。OGLE などにより食連星の大きなリストが出来ている。最近、Guinan et al 1998 は LMC 食連星 HV 2274 の解析を報告した。視線速度と赤化は HST で測られ、測光は Watson et al 1992 を用い、彼らは m - M = 18.47 Plusmn;0.07 を出した。

星への減光　

　しかし、減光の確かさには疑問が残る。彼らは E(B-V) = 0.083 ±0.006 を使ったがこれは非常に低い。 Schlegel et al. 1998 　の与えた LMC 方向平均前景減光が E(B-V) = 0.075 であることを考えると、これは星が LMC の手前にある（これは Guinan et al が HV 2274 が円盤中にあるとしている主張に反する）か、その方向が低減光の窓になっているかである。一方、Harris, Zaritsky, Thompson 1997 の赤化マップの端とこの星は 19' しか離れていない。このマップは星の近くで E(B-V) = 0.15 を示唆している。

　OGLE による減光の再評価　

　減光を過小評価すると距離を過大評価する。そこで、 OGLE による減光の再評価を行った。

　２．観測　

観測ログ　

　HV 2274 は 1998 Seo 9 - Sep 25 の 11 測光夜に観測された。表１にそのリストを載せた。星は微弱星の混入が少ない領域にあり、高精度のアパーチャ測光が可能である。UBVI 等級は Landolt 標準星により標準システムに変換された。

系統誤差　

各晩での V 変換に伴う系統誤差は 0.02 等以下である。一方、B-v, V-I カラーの系統誤差は 0.015 等以下だろう。 U-B カラーのエラーは U バンドでは望遠鏡フィールドコレクターの特性が特殊な為誤差が 0.04 等に拡大する。

　　　　　表１．HV 2274 の測光記録

　HV 2274 の赤化量　

平均カラー　

　HV 2274 の平均カラーは (B-V) = -0.129&plumn;0.007, (V-I) = -0.125&plumn;0.011, (U-B) = -0.905&plumn;0.013 であった。ここのエラーは全観測の標準偏差である。U-B の変換係数は B-V や V-I より悪いので U-B のエラーは &plumn;0.04 まで見こんだ。

二色図上のずれ　

　二色図 (U-B) - (B-V) 上で星の位置から赤化ベクトルを引いて固有位置へ戻す最も古典的な方法を採用した。図１は早期型星の二色図を示す。銀河系の巨星と矮星に対するラインは Schmidt-Kaler 1982 から取った。メタル量の影響を調べるため、Kurucz 1992 モデルグリッド(log g = 3.5、log T = 21,000 - 25,000K)のカラーを計算した。[Fe/H] = 0.0 と -0.5 では (U-B) で 0.019, (B-V) で 0.002 であった。したがって、この程度の精度でなら銀河系星の２色図を LMC の早期B 型星に適用可能である。

赤化の見積もり　

　図１の HV 2274 から赤化ベクトル E(U-B)/E(B-V) = 0.76 (Fitzpatrick 1985) を引いて、E(B-V) = 0.149&plumn;0.015 を得た。HV 2274 はクラスIII と仮定した。

周辺 OB 星の赤化　

　図１上の１１個の黒丸は HV 2274 周辺 3' 内の OB 星である。それらの赤化の平均値は 0.146、標準分散 0.028 である。したがって、HV 2274と周辺 OB 星は同じ程度の赤化を受けていると言える。

図１．二色図上の HV 2274(星印)。実線は巨星、一点破線は矮星。矢印は赤化。
　　　数字のついた黒丸は HV 2274 周囲の OB-型星。

Q メソッドからの赤化量　

　Harris et al 1997 は彼らの Q₁ と Q₂ を用いて赤化マップを作った。この方法を HV 2274 に適用すると、 Q₁ = -0.808, Q₂ = -0.829 となる。それらは、それぞれ E(B-V) = 0.158 と 0.155 を与える。これらの値は２色図から得た赤化とよく一致する。

レッドクランプからの赤化　

　 Udalski 1998 は年齢 2 - 10 Gyr のレッドクランプ I 等級は一定であることを示した。それは僅かにメタル量に依存するだけである。実際、Stanek 1996 はバーデ窓の減光マップをレッドクランプ星を使って作成した。図２a は周辺 150"×150" の二色図である。図２b は 17.2 < I < 19.2, 0.8 < V-I < 1.2 内の星の光度関数である。フィットから決めたレッドクランプ平均等級は ⟨I ⟩ = 18.207 ±0.017、等級分散は σ_RC = 0.18 である。 LMC レッドクランプ星の平均等級は ⟨I₀⟩ = 17.88 （Udalski 1998a）で、フィールド星の平均メタル量[Fe/H] = -0.6 dex(Bica et al 1998) への補正後の値は ⟨I₀⟩ = 17.90 となる。これは、A_I = 0.307 に相当し、赤化としては E(B-V) = 0.157 となる。
Udalski　はいつも傾き効果を無視する。I の安定性は怪しいはずなのにどうして他と合ってしまうのか？

図２b．RC 星の光度関数。区間巾は0.07等。２次式＋ガウシアンでフィット。

図２a． HV 2274 周辺の星の I - (V-I) 図。

　４．議論　

赤化の不一致　

　上で求めた HV 2274 への赤化 E(B-V) = 0.149 ±0.015 は Guinan et al 1998 の使用した赤化 E(B-V) = 0.083 ±0.006 は過小評価であるという推測を支持するものである。これは HST スペクトルにモデルをフィットする際に多くのパラメターが入ってくるためであろう。しかし、今回得た大きな赤化は重大な結果に導く。大きな赤化補正は補正後のフラックスを大きくする。HST スペクトルの最も長波長側 λ = 4800 A では A₄₈₀₀ = 3.8 E(B-V) なので赤化補正フラックスが 0.25 等低く見積もられていたことになる。これを吸収するためには有効温度を上げるか、距離を短くするかの方法しかない。

有効温度　

　有効温度で合わせるには 3000 K 程度の上昇が必要である。しかし、バルマー域のスペクトルをそれで合わせることは難しい。なぜなら、そうするとバルマー線やバルマー不連続の大きさが小さくなるからである。

距離を縮める　

　もう一つの解法は距離指標を 0.25 等短くすることである。Guinan et al は DM=18.47 としていたから 18.22 になる。

LMC 距離　

　LMC に対しての幾何学的補正は行わない。なぜなら、バーの両側にある RR Lyr と RC に対してはまだ確認されていないからである。しかし、最近の LMC 距離評価が短距離に収束していることは確かである。