Miras and Planetary Nebula Formation

アブストラクト 赤色巨星の脈動不安定な外層がミラの振動と似た特性を有することが分かった。 そのようなモデルの進化を追うと、ある点で振動が発散する。力学的計算は この点の先でそのような星が質量を失って惑星状星雲になることを示す。 統計解析からの疑問と中心殻フラッシュの効果を論じる。 １．イントロ　 　赤色巨星外層の流失に依り惑星状星雲が形成されたというアイデアは、 Roxburgh 1967 以来幾つかの論文で検討されてきた。Pacynski,Ziolkovsky 1968 は 外層の断熱解析を行ったが、Keeley 1970 により質量放出には導かないと批判 された。当初の膨張は主に大きな光度によってエネルギーを失い、緩和振動に転化 してしまうからである。しかし、それでも Smith,Rose 1972, Wood 1974 は 振動大気中のショックによるマスロスの可能性を指摘した。ただ、これで本当に 惑星状星雲形成が可能か真剣な検討はなされていない。 　我々は 1978 年に力学的に不安定な赤色巨星外層の構造と運動を調べ、図1にある ように、(L, Te)面上に不安定領域を描き出した。力学的計算に依ると、力学的に 不安定な領域におけるショック質量放出が ≤ 30 yr の短い時間間隔で繰り返される。 すると、進化タイムスケールでは大量の質量の放出が起きる。 　不安定帯内部で色々な質量の星に対して行った計算が全てマスロスを引き起こした。 したがって、この領域に突入した星は安定帯に出るまでマスロスを続けるであろう。 　惑星状星雲形成に関してはこのモデルには以下の欠陥がある：モデル星は外層マスが まだ十分に大きい（Menv > 0.1 M๏）の間に安定帯に逃れてしまう。 一方、惑星状星雲中心星は　Menv < 0.1 M๏ である。 (Osterbrock 1964) さらに Wood 1974 によると、マスロスの開始はもっと暗く、 力学的不安定が始まっていない星で開始される。 　この論文では、前論文より暗く、力学的には安定であるが脈動不安定な領域を扱う。 ここは、ミラ型星が占めている領域である。光度が上がると、周期が伸びることが 分かった。ついにある光度で、力学的不安定になる以前であるが、

脈動が激しくなって マスロスが起きる。上に述べた困難は解消されるようである。これは惑星状星雲の 形成モデルではないだろうか？ 　計算方法とパラメターは論文1と同じである。改良点は、マスロス後にグリッド点を 自動的に付け替えるようにしたことである。この論文は X = 0.7, Y = 0.27 の 種族Ｉ星のみを扱う。 図１　1 M๏星の (L, Te) プロット。太い実線は力学的不安定帯境界。 　　　鎖線はその上でマスロスが起きる境界。実線はPaczynski 1971 の進化。

ミラ　 　ミラ型星の脈動を最初に扱ったのは Kamijo 1963 である。その後 Langer 1969 も動径方向断熱脈動を扱った。その周期から、彼らはミラは基本振動では なく高次の振動を行っていると考えた。Keeley 1970 は流体力学的な計算を行い、 モデルが安定な基準振動で脈動すると報告した。一方、Wood 1974, 1975 は同じく 流体力学的な計算に基づき、高次振動は安定であるが基準振動は発散するとした。 　本論文では、1 M๏ ≤ M ≤ 6 M๏ の範囲 で、進化経路に沿って静的モデルを作り、その力学的解析を行う。図1には 1 M๏ に対する経路を示した。流体力学的非断熱振動モデルに基づき、 半径、光度、温度などの変化を追った。下の表１にはそれらの結果をまとめてある。 周期は線形断熱振動から求まった値である。図２−９には動力学的な特徴を示した。 　i)　ミラの範囲　 　動的モデルの性質を下の表２にまとめた。　 ミラモデルが存在するのは図１０にあるように、LM(M) ≤ L ≤ LPN(M) の範囲である。LM(M) より下では脈動振幅が小さすぎ、 かつ不規則である。LPN(M) より上では脈動が発散し、マスロスが起こる。 　LM(M) と LPN(M) の線形近似式は、 　　　LM(M)/L๏ = 3280(M/M๏) - 1480　　　（２−２） 　　　LPN(M)/L๏ = 8280(M/M๏) - 4680　　　（２−３） 　ii)　基準振動の発生と成長　 　ストリップ（？）中のモデルは全て第１倍音P1で振動している（図２)。 光度が上がると基準振動 P0が現れてくる。そして、1 M๏ の場合で、L = 3200 L๏ になると（図３）、 P0 が P1 と同じくらい大きくなる。そして、と LPN(M) で、 P0 が 支配的となり、もはや振動が定常状態へと緩和されることはない。そしてマスロス が起きる（図４）。Wood 1975 も似た結論に達している。 図３　モデル 1C の動径変化。基本振動 P0が第１倍音P1と 同じくらい強くなる。

図２　モデル 1A の動径変化。第１倍音P1で振動している。 図４　モデル 1D の動径変化。振動が発散し、マスロスが起こる。

iii)　ミラの範囲　 　ある質量の星に対し、周期 P1 は L と共に増大していく。1 M ๏ では 100 日から 250 日まで。P1 は線形断熱解析の 値の近く、少し下に位置する。図１０には準静的ラインが描いてある。 　iv)　周期の一意性　 　図１０からも分かるように、L(Mc) と M の全領域に対し、同じ P を適用できる。 したがって、周期が他のパラメターと 1 対 1 に対応しなくとも驚くべきでない。 実際、原理的には周期を他の観測量、例えば光度曲線の形、と合わせて質量を 導き出すことが可能である。Cahn, Wyatt 1978 はこの方向で研究を進めた。 　v)　周期と質量　 　図１０を見ると、 1 M๏ 以下の星ではミラの周期は 200 日以下 であることが分かる。この議論はなぜ球状星団には 200 日以上のミラがないのか (Feast 1972)という疑問に自然な解答を与える。Iben (1968) によれば、 Y=0.1 では M = 1 - 1.2 M๏ で、Y=0.35 では M = 0.65 - 0.75 M๏ である。 　vi)　光度変化　 　Langer 1969 は輻射等級変化の平均値 ∼ 0.75 等を与えた。これは、 Lmax/Lmin ≈ 2 に対応し、表２と一致する。 Nicholson,Pettit 1933 の半径変化 ΔR/R ≈ 0.36 は我々の ≈ 0.2 より少し大きいが観測のエラーが大きいので許容可能である。彼らの与えた Te ≈ 2000 - 3000 K は表２と一致する。 　vii)　光度曲線のタイプ　 　Campbell 1925 によると、ミラの周期と光度曲線の形には相関がある。Ludendorff 1928 はミラに３種類のタイプを見出した; タイプ α : 急な上昇と穏やかな 下降でやや浅い極小、タイプ β : 対称な光度曲線、タイプ γ ：はっき りしたコブが極小の直前に現れる。Ludendorff は、P ≤ 200 日　のミラは大部分が タイプ β で、一方 P ≥ 400 日　のミラはタイプ α であることを 見出した。タイプ γ は全ての周期に現れ、数は少ない。 図６　モデル 1B の光度変化。M = 1 M๏ タイプ α の光度曲線。 図８　モデル 3B の光度変化。M = 3 M๏ タイプ α の光度曲線。

図５−８はミラがタイプ β からタイプ α へ進化していくことを示す。 図１０ははっきりと、P ≤ 200 日ミラの大部分がミラ帯(Mira strip)の入口に位置し、 一方、P ≥ 400 日ミラはミラ帯後半を占めていることを示す。タイプ γ も見出された。このタイプは P ラインに沿って現れ、それが数の少ない原因と思われる。 図５　モデル 1A の光度変化。M = 1 M๏ タイプ β の光度曲線。 図７　モデル 3A の光度変化。M = 3 M๏ タイプ α の光度曲線。 図９　モデル 6B の光度変化。M = 6 M๏

周期分布　 　図１０と理論的主系列死亡率(Cahn, Wyatt 1976) を用い、ミラ型星の周期分布 （図１１）を予測できる。しかし、観測結果(Wood, Cahn 1977)は, P = 300 - 400 日に切れ目があり、また 100 日 と 600 日方向に急激に低下することを示 している。周期 600 日は 5 - 6 M๏ に対応するので、長周期側 の減少は大質量の星が少ないことで容易に理解できる。しかし、P ≤ 200 日側 の減少はどう理解すべきであろう？ 　その上、ミラの大部分は極大光度が 104L๏ 付近に ある。　ところが、 1 M๏ の星はその半分以下である。したがって、 何かが低質量星のミラを阻害している。 図１０ M - L(Mc) 面上の P = 一定線（細い実線）、数字は周期。太い実線は 　　　　ＭラインとＰライン。 一点鎖線は二つのＦライン。上のＦラインは 　　　　文献から集めたもの。下は Havatzelet,Barkat 1979 による。 　　　　鎖線はＦラインが熱パルスでどう改変されるかを示す。

ミラの寿命　 　Mc - L 関係と水素燃焼エネルギーＱ = 6 × 1018 erg/g とから、 　　　　　d(L/L๏)/dt = 7.66 × (L/L๏) × 10-7 /yr 　　　　　dln(L/L๏)/dt = 3.3 × 10-7 /yr この関係をマスにあまり影響されないミラストリップ（図１０）の巾と合わせると、 ミラの寿命として、 8 × 105 年を得る。 別の研究から、Wood,Cahn 1977 は 7 × 105 年を得た。 彼らはさらに観測的ミラの誕生率として、3 × 10-4 yr-1 kpc-3 を得た。これは惑星状星雲の誕生率 (Cahn, Kaler 1971) に較べ一桁低い。つまり、惑星状星雲の全てがミラ段階を経てきたわけではない。 　三つの困難　 　これら三つの困難（ミラ周期分布の短周期側での減少、低光度（低質量）ミラの 不足、惑星状星雲との誕生率の不一致）はダブルシェルの存在を正しく考慮すると 全て解決するが、詳しい議論はマスロスについて調べた後に行う。 図１１ 周期分布 dn/dlogP 対 P を示す。ここに n(P) は、周期 > P のミラ数/ kpc3 である。太い実線は Wood,Cahn 1977 の観測。一点鎖線は理論曲線。 ３本の鎖線は低質量星を落とした理論曲線。付けた数字は MT

惑星状星雲の形成　 　惑星状星雲の形成過程を調べるため、1 M๏ の進化を脈動が 発散（表１のモデル１Ｄ）する段階から調べる。 　図１２を見ると分かるように、 初めは第１倍音振動が主であるが、約１０年で基底振動が支配的になり、振幅が 増大する。&Delra;R ∼ R になると、部分的電離層の上にある輻射層が透明 になる。光度が上がり、輻射で失われるエネルギーが外層の熱エネルギー （大部分は再結合で放出された分）と同じくらいになる。 　この過程は非常に 短時間で、このため運動が逆転した時には深い陥没を示す。この層は膨張の時に 再結合を起こした領域で、ソフトつまり小さい γ を有する。一方、深い層は その間電離したままで、質量当たりのエントロピーを保持しており、相対的には 堅い壁として振る舞う。このため、強いバウンスが起き、ショック波が立つ。 　膨張ショックの物質は再び再結合エネルギーを放出し、圧力を維持するので、ショック 波は外層を押し続ける。最終的には外層の 3 % を占める最外層の約２０％が脱出速度 を得て星の外へと飛び出す。この数値計算では外層は１００層、最外層は３０層に 区切られており、放出されたのは５−８層である。 　この時点で、残された物質は逆転し、穏やかな振動を繰り返す。外層に注入される コアからのエネルギー L は表面光度 LS よりずっと大きいので、外層 物質の内部エネルギーは増大していく。内部エネルギーが大きくなると振幅が増大 していく。そして、前回のレベルに達すると再び膨張ー収縮ー放出過程が繰り返される。 　この内部エネルギー充填時間 Δte は質量放出の間隔と等しい のであるが、次のように導くことができる： 　失われたエネルギー ΔE は外層の再結合エネルギーのある割合 α を 占める。エネルギー収支は次のように表わされる。 　　　ΔE = α εi Me ≈ ∫(L-LS)dt ≈ (L-LS)Δt ≈ LΔt 上の式に εi ≈ 1.3 × 1013 erg/g （水素電離エネルギー）を入れ、 　　　　　Δt = α εi Me/L ≤ 2 × 105 (me/l) yr ここに、me = Me/M, .　l = L/L๏　である。 l に（２−３）式を使うと、 　　　　　Δt( m, me) ≤ β(m)me　　　（２−８） β(m) は m に対し β(m=1) = 50 から β(m=6) = 5 へと単調に減少する。 近似的に以下の式で表わされる。 　　　　　β(m) = 54/m - 4 マスロス開始時の me ( &eqiv; mep)を（２−３）、 （２−１）式で表現して、次の式に到達する。 　　　　　meR ≈ 0.86m - 0.44

これは、（２−８）式を使うと、最初のΔte に対し、 　　　　　Δtep(m) ≤ 48.2 - 3.44{m + (6.91/m)} 年 この式は 1 ≤ m ≤ 6 ではあまり m に依存せず、 　　　　　Δtep ≤ 25 年 　外層の運動を１３０年間追った。その間４回の質量放出が起き、全部で外層の 12 %, 0.05 M๏ が失われた。図１２はこの過程は半規則的であることを 示唆する。 　計算を続けるのは時間とお金がかかるので、代わりに外層質量を変化させて 静的モデルから出発させた。すると、同じ L, Mc で外層質量を 0.1 M๏ 減らしたモデルでは 40 年間に　0.03 M๏ の放出、外層マス を 0.002 M๏ のモデルでも質量放出が見られた。最終的に のこる外層マスは 0.001 M๏ 以下なのではないか。 　毎回、最初と同じ外層の 3 % が失われるとすると、放出間隔が m に比例するので、 　　　　　ΔtPN < ΔtePΣ0.97 n = 33tPN = 825 年 この評価は Paczynski 1973 の観測的評価とも一致する。放出速度は脱出速度に 近く、外層が薄くなると高速化していく。したがって、後からのガスは前のガスに 追い付き、惑星状星雲を作るのであろう。 図１２　モデル１Ｄ：1M๏, 脈動が発散し始める時期、の動径変化。 　　　　矢印は質量放出を示す。

　３．議論

ミラ寿命の切り下げ　 熱パルス強度とミラ帯　　次に図１３に行こう。この図の縦軸 Δlog L は熱パルス強度である。　（熱パルス強度は ある M でも Mc と共に変化するはずだが。少ない計算例 から引いたからそうなったのか？）　水平線はミラ帯の巾 (ΔL) M で、一緒に熱パルスに伴う光度変化（Δlog L）の計算例を載せた。 文献からの計算結果は色々と異なる仮定の下でなされており、まとめるのは困難で あった。例えばGingold 1975 では熱パルスに伴う光度変化が全くない。 　熱パルス強度 Δlog L とミラ帯 (Δlog L)M を一つの図中に並べる意味が分からない。 熱パルス強度 Δlog L のラインが ミラ帯の巾 (Δlog L)M ライン と M = M∗ で交差するとしよう。その場合、M < M ∗ では、星が間パルス期でもミラになる以前にＰＮ形成が起こると結論する。 Δlog L と Δlog L)M を較べる意味が不明。 Δlog L = log L(パルスピーク)ーlog L(間パルス), Δlog L)M = log L(ミラ基本振動開始) - log L(ミラ開始)　なので、 Δlog L - Δlog L)M = [log L(パルスピーク) - log L(ミラ基本振動開始)] -[ log L(間パルス) - log L(ミラ基本振動開始)]となる。したがって、 L(間パルス) ≈ L(ミラ基本振動開始) ならば、図１３は L(パルスピーク) と L(ミラ基本振動開始)とを較べることになる。その場合、M∗ は熱パルスピークが基本振動ミラ光度と同じくらいになる質量と言える。 　もし、熱パルスの項の最後での仮定と逆に、パルス期の長さが短く、Δ tf ≤ 103 年だと、ある量が各パルス毎に放出される。 その場合は多重シェルＰＮ形成を期待できる。注意しておくが、観測との一致を 求めるならば、観測から決まるシェル間の放出間隔がパルス間隔と合致する必要がある。 この点に関してはここでは論じない。 　実際、Sackmann 1976 の 3, 6 M๏ に対する Δlog L を 低質量側に外挿すると、 M∗ ≈ 2 M๏ を得る。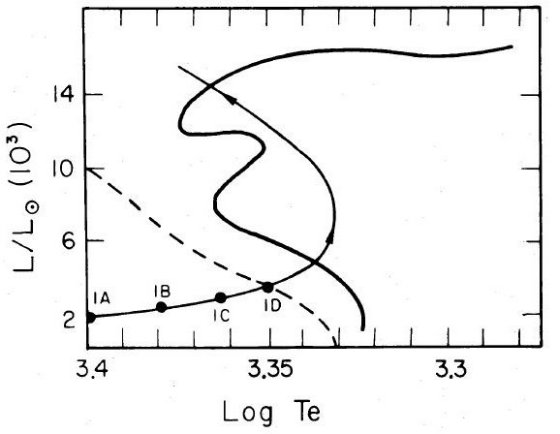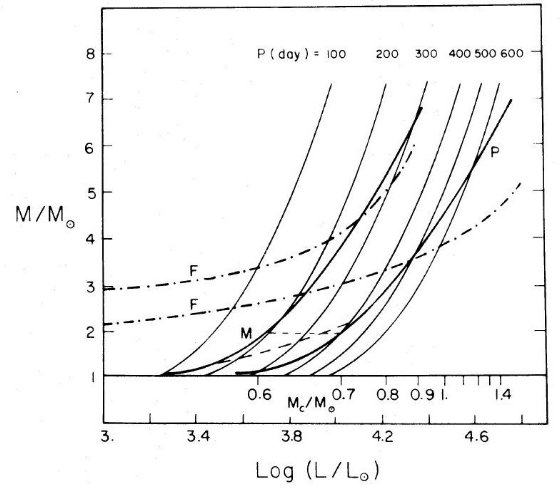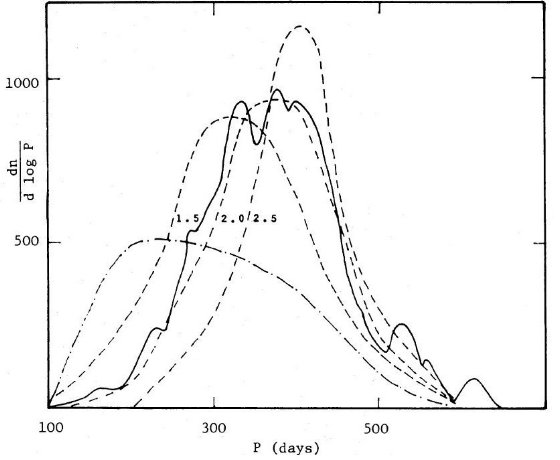また、文献によるとどうやら、tf ≤ 103 年 らしいので、ミラの寿命は 2 M๏ では大幅に切り下げられるよう である。図１３には細い鎖線でその場合のＰ線を書き込んである。そのように、 M ≤ 2 M๏ でミラ寿命を縮めた場合のミラ周期分布を図１１に 示してある。この新しい分布が観測と合うことは明らかである。 ミラ寿命の絶対値　　ただし、この一致は規格化した分布でのことで、寿命＝ 8 × 105 年を仮定して、ミラ数密度の絶対値は依然として大きすぎる。切り下げを行う前で ミラの数密度は、 1792 kpc-3 であり、 2 M๏ 切り下げ 後は 672 kpc-3 である。Wood,Cahn の観測値は 245 kpc-3 で 有意に小さい。定常マスロス、Mc - L 関係の見直しなどにより、この差を縮めることは 可能と考えられるがまだ実施に至っていない。 Wood,Cahn 1977 との比較　 　Wood,Cahn 1977 は (m,l)面 (これ何だ？)　　上で ミラの位置を観測的に決めた。しかし、それは今回の結果と決定的に違っていた。その 原因は以下の通りである： (a) ＨＲ図上のミラの分布に関し、今回のモデル位置はＷＣより低温側に寄っているが 古いNicholson,Pettit 1933 とは合っている。モデルの位置は対流混合距離の 取り方で移動する。我々は (l/H) = 1.0 とした。このパラメターの調整でＷＣと モデルを一致させることが可能である。おなじ (m,l) に対し、ＷＣとわれわれとでは 異なる R を採用し、そのため異なる P を得た。このため、我々の図３にある等周期線 はＷＣに比べ左にずれたのである。 (b) WC の方法は、観測周期分布を再現するよう、トライアルアンドエラーで ミラ帯を探している。境界が(m,l)面で直線の3角形を仮定した。底辺を 0.6 M๏ （250 ≤ P1 ≤ 450）に置き、 頂点を 1.5 - 2 M๏ （ P1 ≈ 600）とした。

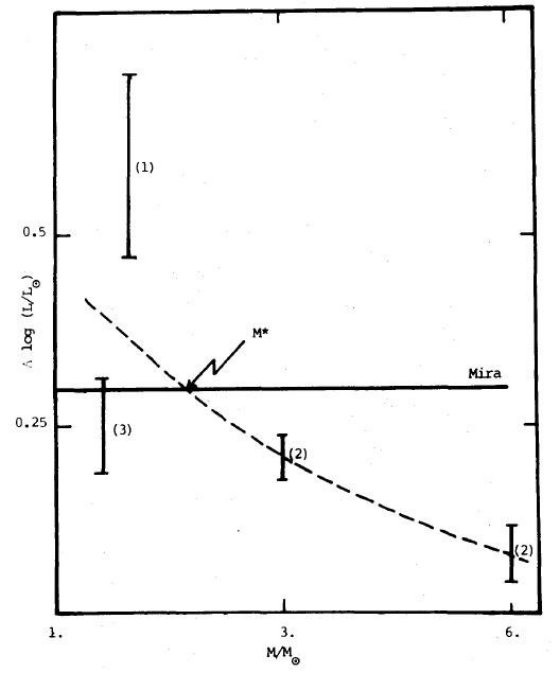
図１３　熱パルス強度(Δlog L)の星質量による変化。縦線は計算例。 　　　　(1)=Schwartzschild,Harm 1967, (2)=Sackmann 1976, (3)=Gingold 1974 　　　　水平実線はミラ帯(Δlog L)M 　これに対し、我々のミラ帯は全く違う形をしている。特に大質量側に伸びている 点が違う。観測分布を再現するためにはダブルシェル燃焼によるミラ帯の剥ぎ取り が必要である。WCは熱パルスが l の減少のみに関わるとしている。しかし、これは 前に指摘したように必ずしもそうではない。 星風　 　定常質量放出に関し、Wood 1974, Scalo 1976, Fusi-Pecci,Renzini 1975 WC, Mengel 1976 は　Reimers 1975 型の星風の影響を調べた。しかし、 我々が指摘したように、低光度でかなり（ミラを停止させるほど）の質量放出 を起こしており、定常星風ではそれには足りない。 星風　 　組成比、混合距離などのパラメターの影響は全く考慮していない。 それらを入れた計算は高価になりすぎるから。われわれはしかし、それらの 正確なパラメターの値に関わらず、マスロスが起きていることは確かである ことを示した。その正確な形（M,L面での）や巾の値そのものは現時点では 不確実である。それでもこの仕事の重要な点は、内部無矛盾性にある。