Extinction Map of the Galactic centre: OGLE-II Galactic bulge fields


Sumi,T.
2004 MN 349, 193 - 204


　アブストラクト

OGLE-II 銀河系バルジフィールド 48 個に対し、A(V), A(I) マップを作った。領域の総計は 11 平方度である。測定には RC 星の V, I 測光が用いられた。A(V)/E(V-I) = 1.9 - 2.1 という 異常値を得たが、それは Udalski の結果と一致している。平均値 R(VI)=1.964 (sdev=0.085)を 使用して E(V-I), A(V), A(I) のマップを作った。空間分解能は 26.7 - 106.8 秒角と高い。 レッドクランプ星 の 固有カラーは一定と仮定した。マップの範囲は 0.42 < E(V-I) < 3.5, 0.83 < A(V) < 6.9, 0.41 < A(I) < 3.4 に及ぶ。マップのゼロ点は バーデの窓中の RRab 型 RR Lyr 星 20 個の V-K カラーから較正された。l = +5&\deg;& から -5&\deg;& の 間に赤化補正後のレッドクランプ見かけ I 等級は 0.4 mag 変化した。これは星がバーに 乗っていることを示す。バルジの RRab, レッドクランプ星のカラーが異常と言う研究があった が、赤化補正した値は正常であった。

　1.イントロ　

過去のマップ　
Schultheis et al 1999　4 arcmin マップ　　上部 RGB の J, K (DENIS)
Dutra et al 2003　4 arcmin マップ　　上部 RGB の J, K (2MASS)
Kiraga, Paczynski,Stanek 1997 BW の減光マップ。RC 等級
Gould,Popowski,Terndrup 1998 BW の減光マップ。K-巨星 等級
Alcock et al 1998 　BW の減光マップ。　　RR Lyr　等級
Popowski,Cook,Becker 2003 バルジ大規模減光マップ。MACHO全星平均カラー


　Wozniak,Stanek 1996 の方法　
　OGLE-I 小領域の CMD で RC の平均 V, V-I を決める。それらが一直線に並ぶので その勾配から
　　　　　　R(VI)=A(V)/E(V-I)=2.44
を得た。 		Wozniak,Stanek 法の例　
Stanek 1996 バーデの窓+OGLE-I 40x40 arcmin で R VI = 2.49 ± 0.02
Paczynski et al 1999 OGLE-II 14.2 x 14.2 arcmin
　　　　　分解能 20 arcsec E(V-I) 赤化マップをまず作り、それに
　　　　　A(I)=R I *E(V-I), A(V)=R VI *E(V-I)
　　　　　を適用して、減光マップを作った。
　　　　　標準値、R VI = 2.5, R I =A(I)/E(V-I)=1.5 が使用された。
Sumi et al 2003 MOA 　　16 平方度　分解能 3.45 x 3.45 arcmin で同じ方法。

　異常？
Paczynski,Stanek 1998, Stutz,Popowski,Gould 1999
　　バルジの RC, RR Lyr を Stanek の赤化マップで直すと、近傍より赤い。
Popowski 2000 バルジ方向の減光則が異常。R VI = 2.1 (標準値2.5)採用？
Udalski 2003 実際に、 R VI = 1.9 - 2.3 で、方向により変化する。


　この論文
R(VI) の異常を確認する。新しい値を用いて、OGLE-II 48 領域の減光マップを作成する。

　２．データ　

　OGLE-II　
49 フィールド 3千万星の V, I 測光。ただし、BUL_SC44 は減光が強いので使用できなかった。 		　測光　
　星の測光等級は数百観測 1997- 2000 の平均値。測光ゼロ点の精度= 0.04 mag.

3. RI = AI/E(V-I) の決定

(V, V-I) 対 (I, V-I)　
Io,RC は(V-I)に対し一定だが、Vo,RC は(V-I) により変化する(Paczynski,Stanek 1998)。 このため、V(RC) は赤化補正で系統誤差を生じる(Popowski 2000)。
仮定：(V-I)o,RC = 1.0 で一定。
I(RC)=Io,RC+R(I)[(V-I)RC-(V-I)o,RC]

第１ステップ　
ビン＝128 x 128 ピクセル。各フィールド＝ 16 x 64 ビン。
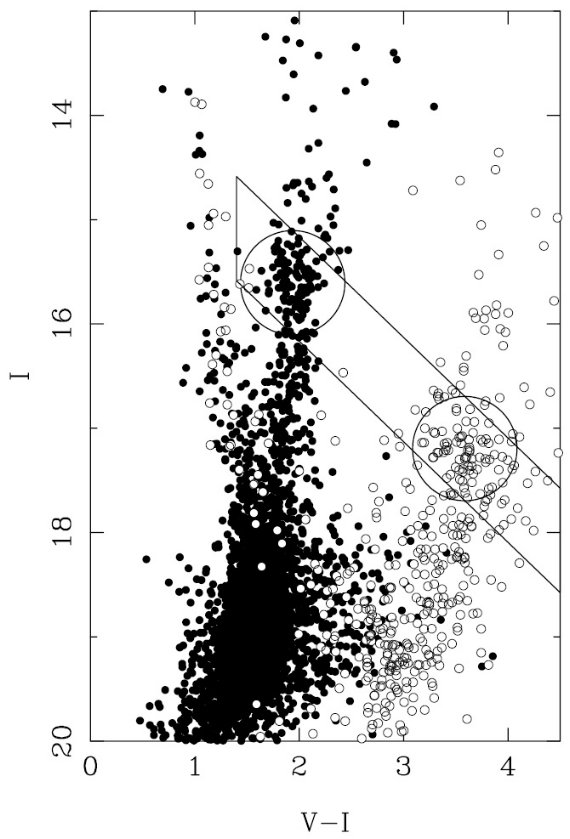
ビン内の微分赤化ーー＞RC 星が赤化ベクトル方向に伸びる。
2 σ クリッピングにより、ビン内平均 RC 等級、カラーを求める。この 逐次近似を収束するまで続ける。初期値は 0.6< R(I) <2.0, 14 o,RC < 15 の範囲ではどれでも同じ値に収束した。

　第２ステップ　

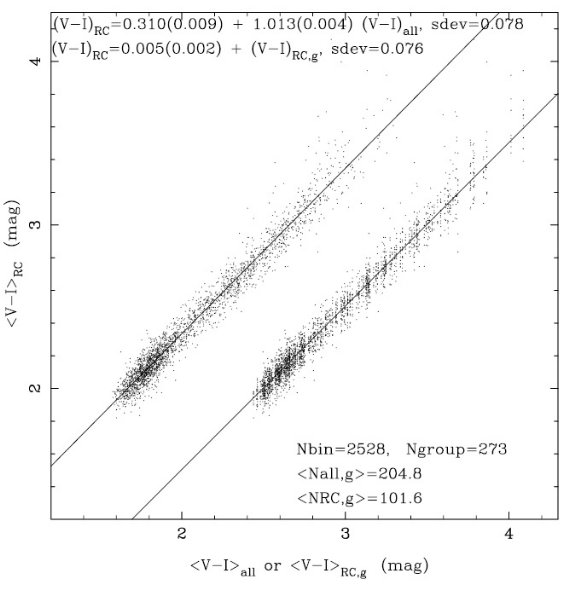
与えられたフィールド内のビンを ⟨V-I⟩RC の順に並べる。
ビンを低減光から高減光へとグループにまとめる。グループ内の RC 数は約1000
グループ毎に CMD 上で RC 位置を決める。

　ガウシャンフィットの手順は省略する。


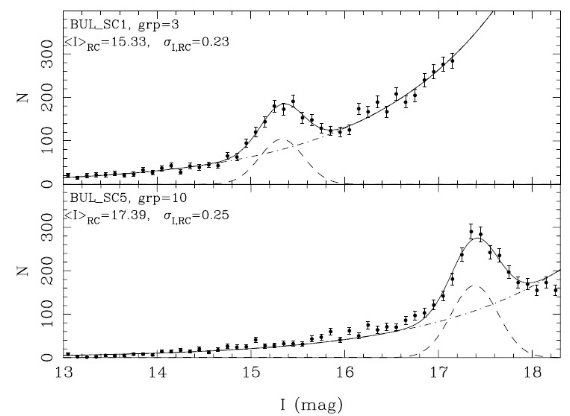
図 1．上＝低減光（BUL_SC1,group=3）下＝高減光（BUL_SC5,group=10）光度関数。 		　フィールドから領域へ　
　４４個の OGLE-II フィールドをたがいに近いもの同士集めて１１領域にまとめ、 表１に示した。領域 A, B, C, D は Udalski 2003 と同一である。フィールド BU+-SC6, 7, 47, 48, 49 はレッドクランプの数が少なすぎたので解析しない。
仮定：赤化線の勾配=RI は各１１領域内では同じと考える。
　　　しかし、異なる領域では違う値になるかも知れない。


　階層を整理しておくと　

　ビン　　　＝128 x 128 ピクセル。
　グループ＝ ⟨V-I⟩RC の順に並べたフィールド内ビンを
　　　　　　　　1000 RC 区切りでまとめたもの。ここで RC centroid 決定
　フィールド＝ 16 x 64 ビン＝何個かのグループに分けられる。
　領域　　　＝近接フィールドの集まり。１１個ある。

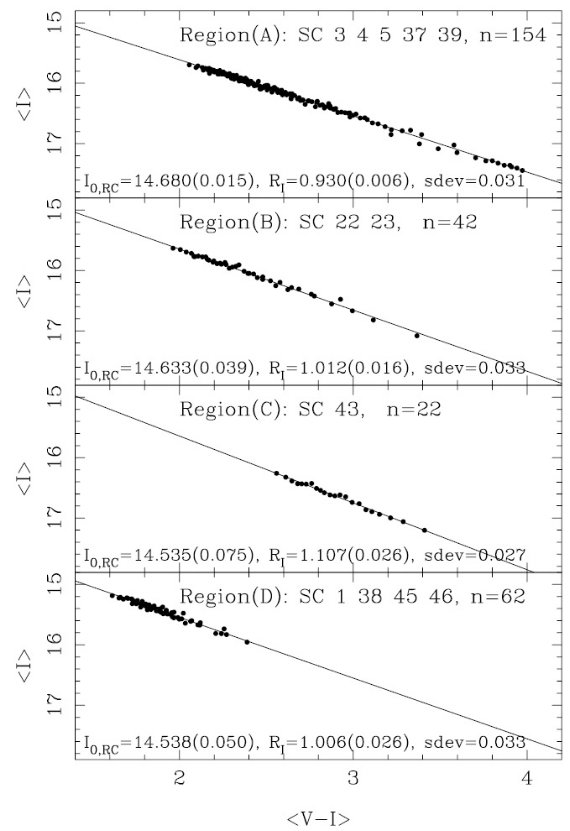
したがって、各領域にはビンを集めたグループが複数個あり、各グループは RC 中心値 ⟨V-I⟩RC, ⟨I⟩RC を持つ。 これらのデータを各領域ごとに、
　　　　　⟨ I ⟩RC = ⟨ I ⟩o,RC + RI ( ⟨ V-I ⟩RC - ⟨ V-I ⟩o,RC )
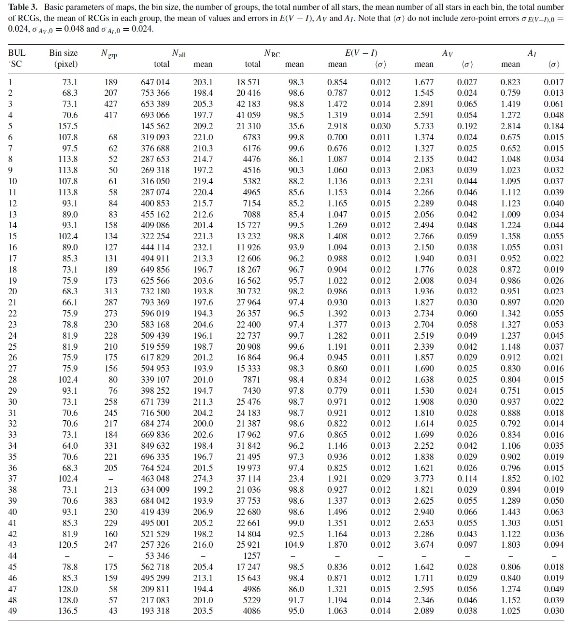
でフィットして、RI と ⟨ I ⟩o,RC を決める。結果は下の 表１に示した。


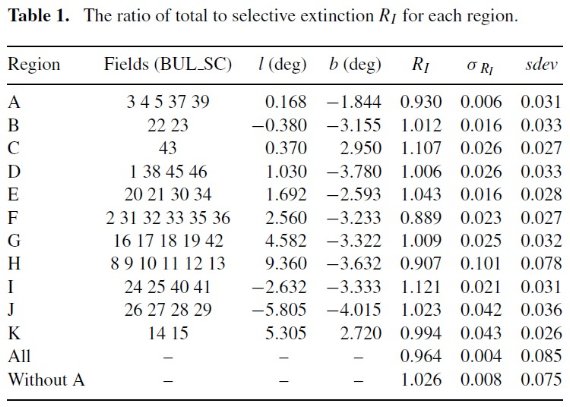
表１．各領域での選択対総減光比 RI
　小さな R I 　
　図２では領域 A, B, C 内の各グループで決めた、レッドクランプ中心の ⟨ I ⟩ - ⟨ V-I ⟩　CMD を示す。ベストフィットライン から決めた R I = A I /E(V-I) は表１に載せた。
　得られた R I は標準減光則で与えられる R I = 1.5 よりかなり小さく、これは Udalski 2003 の得た結果と一致する。


図２．領域 A, B, C 内の各グループで決めた、レッドクランプ中心の ⟨ I ⟩ - ⟨ V-I ⟩　CMD。図中にベストフィットラインのパラメタ―を示す。　 		　 R I と l, b との関係　
　図３には R I と l, b との関係を示す。系統的なパターンは見えない。 そこで、この先では全体の平均値 R I = 0.964 と sdev = 0.085 を用いる。


図３．各領域で決めた R I = A I /E(V-I) と 銀経 l （上） 銀緯 b（下）との関係。

表２．各領域で、平均の R I = 0.964 を用いて、減光補正したレッド クランプの I o,RC を示す。I* o,RC はゼロ点補正をした あとの値。

図４．各領域で決めた I o,RC と 銀経 l （左） 銀緯 b（右）との関係。Stanek et al 1997 と同じく明らかなバーを示す。領域 C, K は b >0 で他領域と反対側にあるが、図でもずれている。何を意味するか？


　４．減光マップ　

　４．１．相対赤化　


図５．BUL_SC22 中の二つのグループ(白丸と黒丸)の CMD. 平行四辺形は レッドクランプ星を選択するためのスタート領域を示す。二つの丸は 各グループでのレッドクランプ。 		　ビン毎に E(V-I) を求める際の仮定　
(V-I)o,RC = 1.0
R I = 0.964
Io,RC = 各領域ごとに表２で与えられた値を採用

　新しいビン　
新しいビンサイズ＝ 64x64 から 157x157 まで各ビンが大体 200 星を含む大きさに選ぶ。 このビンで平均ＲＣカラーを求めた。


図６．BUL_SC22 フィールド中の全てのビンに対し、縦軸＝レッドクランプの (V-I)RC. 上線の横軸＝ビン内の全ての星の平均カラー、(V-I)all. 下線の横軸＝各グループのレッドクランプ星の平均カラー、(V-I)RC, g. 見易さのため、下線は +0.5 足した。


　４．２．ゼロ点

　Alcock et al 1998 の方法　
これまで、全フィールドでレッドクランプ平均カラーは一定とし、メタル量 依存性などは無視してきた。⟨ V-I ⟩ o, RC のゼロ点は Alcock et al 1998 の方法で較正した。図７には 4.1.で求めたレッドクランプの A V, RC と Alcock et al 1998 が決めた 20 RRab 星の A V, RR との差を示した。オフセットの平均値は ⟨ A V, RC - A V, RR ⟩ = 0.055±0.048 である。
オフセットが生じたのは、第３章の初めで仮定した(V-I)o,RC = 1.0 で一定、 が悪かったと考える。オフセットを消すためには (V-I)o,RC を 0.055 × E(V-I)/Av = 0.055 / R VI = 0.055/2.5 = 0.022 増やして、 1.022 (本文では 1.028 となっているが。)とする必要がある。 これは、A I オフセットとしては 0.055 × (R I /R VI ) = 0.055 × (1.5/2.5) = 0.033 (RL85 では A(I)/A(V)=0.48 となるのだが。ここの 2.5, 1.5 は変だな。) に相当する。これが表２で I* o, RC で 0.027 の補正が 加えられている理由である。


図７．4.1.で求めたレッドクランプの A V, RC と Alcock et al 1998 が決めた 20 RRab 星の A V, RR との差。


表３．Av 減光マップのパラメタ―。ビンのサイズ、グループ数、星全部の数、ビン当たりの 平均星数、レッドクランプの総数、グループあたりの平均レッドクランプ数、E(V-I), Av, A I の平均値。⟨σ⟩ は相対マップ中の統計誤差であり、ゼロ点 系統誤差は含まない。



図８．Av マップ。離れた場所は箱の中。


　　　　　この後の RR Lyr を使ったチェックの部分は省略。


　５．議論　

　赤化異常　
　R VI = A V / E(V-I) = 1.9 - 2.1 と小さいという Udalski 2003 の結論が確認された。これは、おそらくダストサイズが小さくなっていることを意味する。

　減光マップ　
　平均値　R VI = 1.964 を用いて、 48 OBLE-II GB フィールドで Av, A I マップを作成した。これは -11 < l < +11 に渡っている。測られた減光範囲は、 0.42 < E(V-I) < 3.5, 0.83 < Av < 6.9, 0.41 < A I < 3.4 である。マップの空間分解能は 26.7 - 106.9 arcsec である。

　減光ゼロ点　
　減光ゼロ点の較正はバーデ窓中の 20 RRab を使って行った。 		　レッドクランプ絶対等級　
　減光補正後のレッドクランプ I 等級は、バーデ窓で、 I* o,RC = 14.6 と 予想より暗い。銀河中心距離を 14.52 mag (Eisenhauer et al 2003) とし、太陽近傍の レッドクランプ I 絶対等級、 M Io,RC = -0.26 ±0.03 (Alves et al 2003) を使うと期待値は、I o,RC = 14.52-0.26 = 14.3 だからである。
　種族効果が大きい(Salaris et al 2003, Percival, Salaris 2003), 銀河中心距離が もっと大きい、赤化がもっと複雑低減光で勾配が変わるなどの説明が可能だが確かでない。