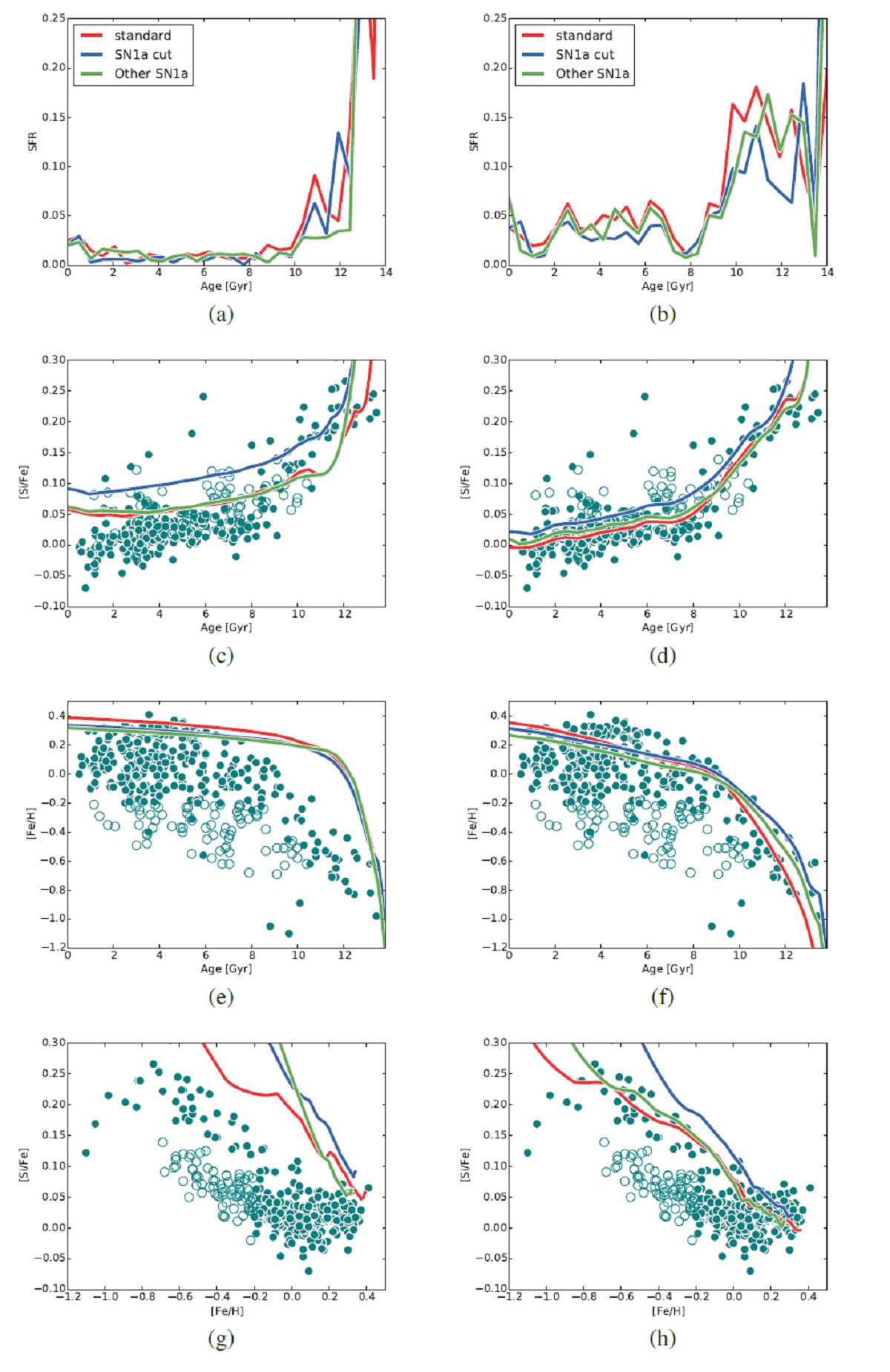
2.2.化学進化経路の作成
化学進化経路を計算する各段階ここはコード中で、化学進化経路を計算する部分である。それは以下の 段階で遂行される。
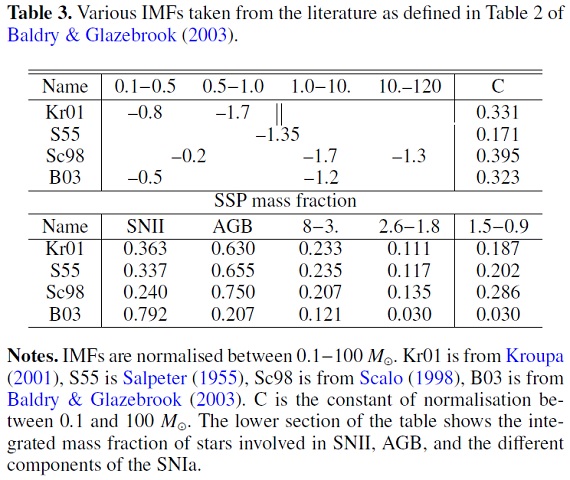
(1) IMF を選ぶ。(例えば Kroupa01)
(2)SNII, AGB, SNIa のイールドを選ぶ。
(3)星の寿命を求める。
(4)(Z, t) での SNII と AGB である星の質量比を計算する。
(一瞬の SNII 星の質量比? )
(5)(4)にイールドを掛ける。
(6)SNIa の遅延時間の定式化。それに SNIa イールドを掛ける。
(7)累積イールドを時間と共に計算する。
この部分はある時刻に、星間空間に戻されるガス、メタルの量、 SNIa, SNII の数などを初期メタル量毎に計算する。
SNII イールド
SNII イールドには Nomoto06 を用いる。SNII の最小質量は 8 Mo とする。 (Few12, Kawata,Gibson03)イールドは星質量に対する表で与えられる。 モデルでイールドが与えられている星は < 40 Mo に限られる。それ以上の 星に対して 40 Mo のイールドを適用すると Si 量が説明できない。この問題は 将来に待つ。
星の寿命
Raiteri96 は星寿命の近似式を次のように与えた。
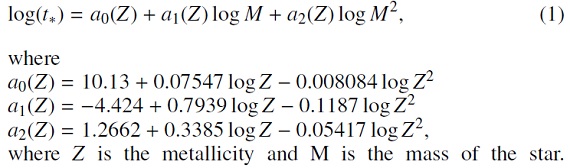
この式は Z = [7 10-5, 0.03] で妥当である。モデル計算では 我々は上式を M(t) の形に変換して使う。
(Raiteri96 の式と3箇所に誤りがある。 )
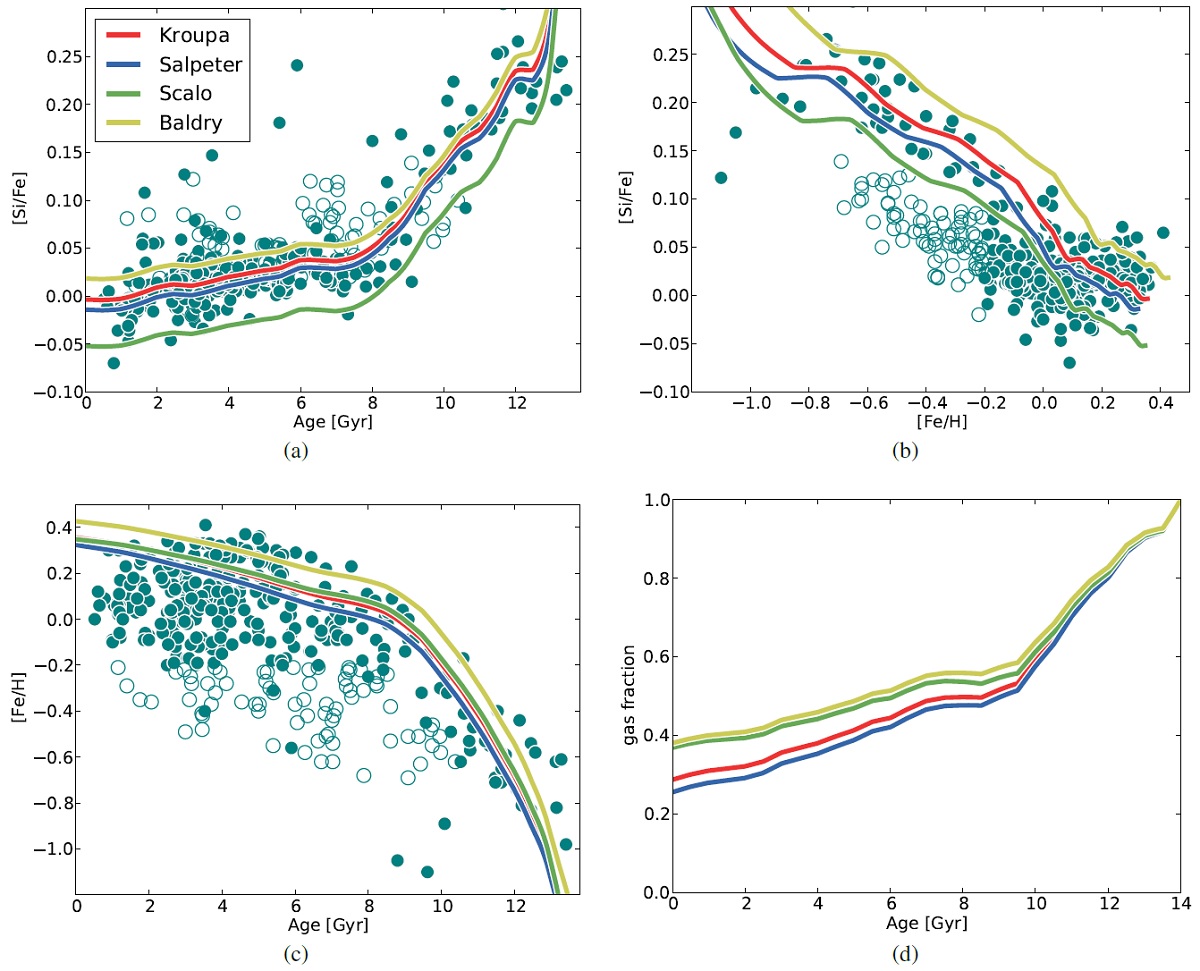
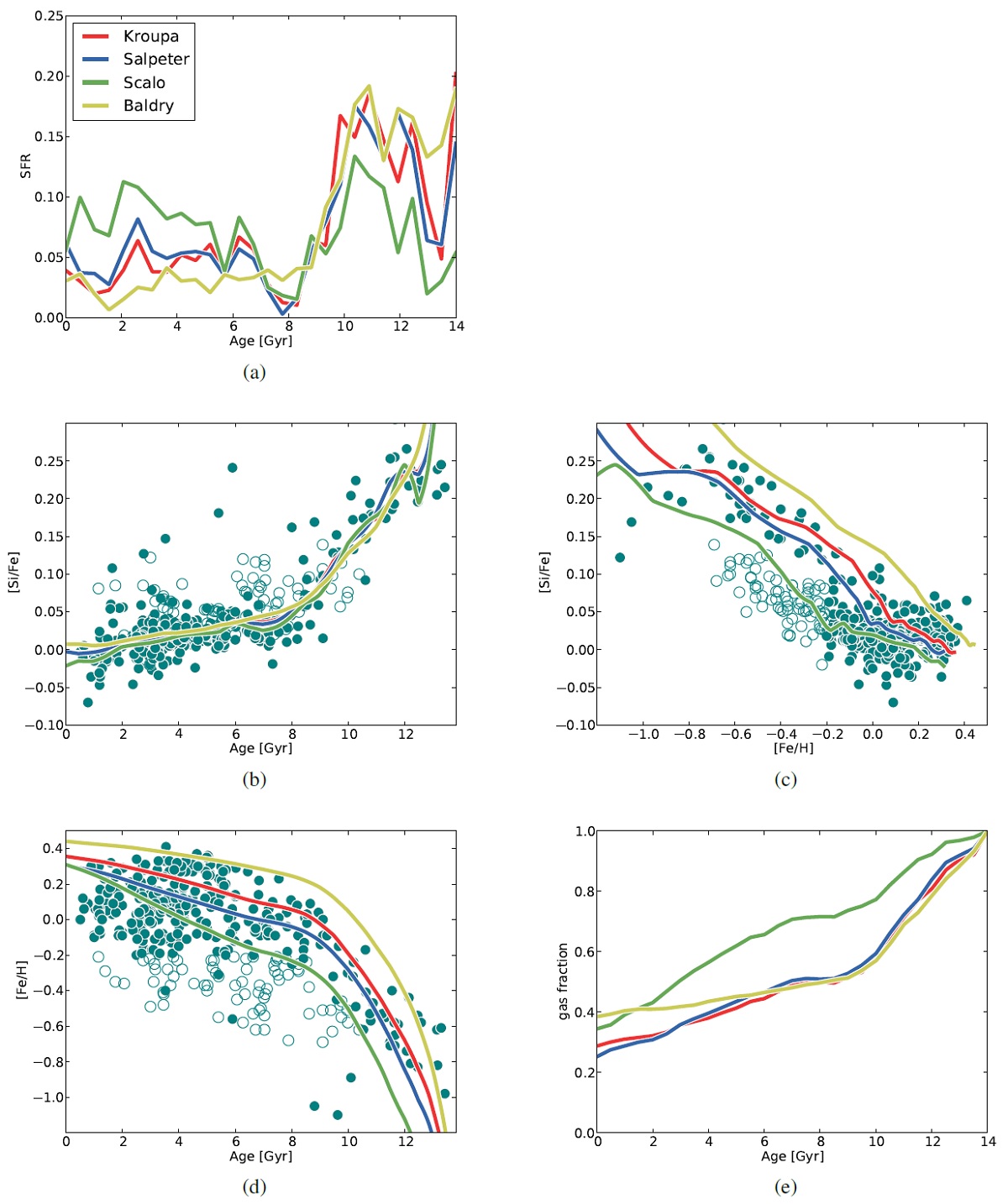
Kroupa01 の IMF を採用した。
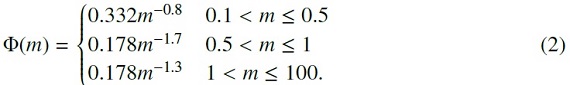
積分イールド
イールド、寿命、IMF を結合して、 積分イールド Γ(t=now) を次の形で得る。
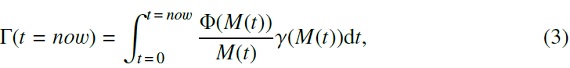
ここに、Φ(M(t)) = 時刻tで死ぬ星の IMF. γ(M(t)) = 時刻 t に 死ぬ星のイールド。
(意味がピンとこない。SFH が式に 入っていない。"t=now" が何を言おうとしているのかはっきりしないが、"now" を銀河形成以来の固定値でなく、ある任意の t を指す変数と考える。 また、IMF は単位質量に規格化されているらしい。すると、"now" の昔に IMF 質量分布で形成形成された星が、その後現在までに放出する総量を与える式と 考えればよい?)
SNIa のイールド
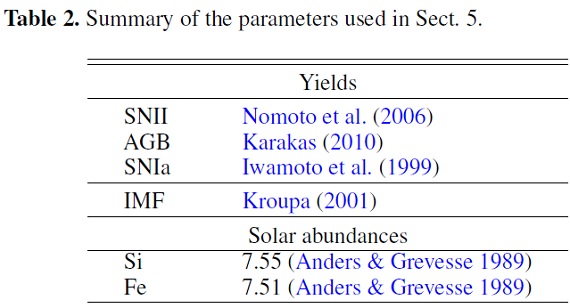
SNIa の元素イールドは Iwamoto99 から採った。超新星率は Kawata,Gibson03 を採用した。それ自体は Kobayashi00 からのものである。このモデルでは母星系 を二つに分ける。一つは白色矮星+赤色巨星、もう一つは白色巨星+主系列星、 である。SNIa による遅延は 1 - 2 Gyr である。我々は SNIa が白色矮星を完全 に破壊し、 1.38 Mo を還流すると仮定する。水素の還流量は 0.01 Mo でほぼ ゼロである。Kobayashi00 のようにあるメタル量以下では SNIa は起こらない という意見もあるが、ここではこの意見は採らない。
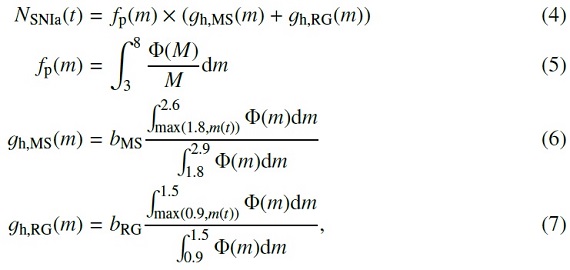 ここに、NSNIa = 超新星数の時間変化。Φ(m) = IMF. 積分範囲
の 3 - 8 は白色矮星に進化する星の質量範囲である。(2.6, 1.8) と (1.5, 0.9)
は白色矮星にガスを供給する主系列星と赤色巨星の質量範囲である。二重白色矮星
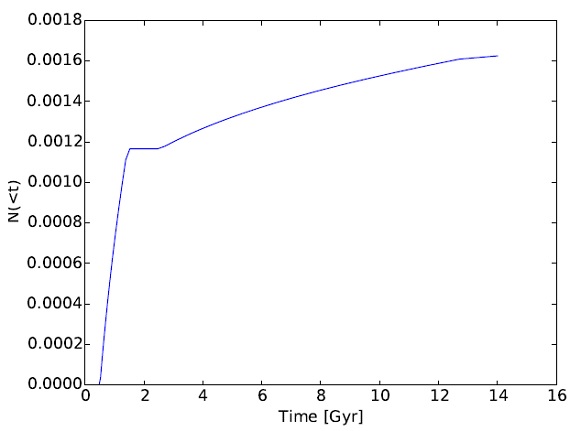
モデルは考えない。SNIa の累積数を図 1 に示す。
ここに、NSNIa = 超新星数の時間変化。Φ(m) = IMF. 積分範囲
の 3 - 8 は白色矮星に進化する星の質量範囲である。(2.6, 1.8) と (1.5, 0.9)
は白色矮星にガスを供給する主系列星と赤色巨星の質量範囲である。二重白色矮星
モデルは考えない。SNIa の累積数を図 1 に示す。