Star Counts Redivivus IV. Density Laws throughout Photometric Parallaxes


Siegel, M.H., Majewski, Reid, Thompson, J.N., Soneira, R.M.
2002 ApJ 578, 151 - 175



　アブストラクト

測光視差　

　銀河系恒星成分の分布を決定するため、７つのカプタイン選択領域内の星に対する測光 視差の解析を行った。領域全体 14.9 平方度にある 13 万星のうち 7 万星のカラーは 0.4 ≥ R - I ≥ 1.5 で、このカラー範囲は測光視差の精度が良い。論文では測光 パイプライン、測光視差の決定法を述べる。さらに、マルキストバイアス、巨星、準 巨星の混入、メタル量、連星の影響を調べた。これらの内、連星の影響が最も大きい。 連星比率が 50 % あると、解析結果が実際のスケール高の 80 % になってしまう。

円盤のスケール高　

　7 領域の同時解析からは天の川銀河の円盤種族に制限をかけることが出来た。しかし、 ハローに対してはよい解がみつからなかった。我々は他の研究から決められたハローの 密度分布を採用し、Besancon 平坦べき乗則モデル、c/a = 0.6, ρ ∝ r -2.75、が最適フィットを与えることを見出した。 		　このハローを用いると、 厚い円盤はスケール高 = 750 pc で古い円盤の 8.5 % 規格量である。古い円盤の スケール高は早期型矮星(5.8 ≤ MR < 6.8) で 280 - 300 pc、 晩期型矮星(8.8 ≤ MR < 10.2) で約 350 pc である。連星率 50 % の補正をすると、上の値は 940 pc と 350 - 375 pc となる。

観測とモデルとのずれ　

　この方法によっても、観測分布とモデル分布の間にはずれが残る。ずれは我々の サーベイの検出限界のところで起きた。特に我々のモデルは銀河系内側部分で過大 密度を、外側で過小密度を与える。このジレンマを逃れるためにはハローを２成分系 と考えると良い。このハローモデルは水平枝 RR Lyr 星の研究、低メタル星の運動 の研究からも支持されている。この観点からはハローの内側は平坦で外側は球形と なる。さらに、厚い円盤がめくれていると考えるとさらに一致が良くなる。この めくれは厚い円盤の起源をマージャーと考えると予想される現象である。

　1.イントロ　


古い星の意義　

　天の川銀河の現在の星成分は銀河の形成と進化の化石である。銀河面のように 混乱した領域では星形成時の運動学、化学的性質は短時間で混ぜ込まれてしまう。 遠隔の場所では古代の星が語る話はいまだに本当である。低質量星の寿命は ハッブル時間より長いので、それらは銀河の遠い過去のこだまとして存在し続け ている。古い星からの伝言を読み解く最良の方法はそれらを似た性質の星の グループ、すなわち星種族に分けることである。

種族の有効性　

　銀河系の星の分類はバーデ(1944)の種族 I と II の分類で大きく前進した。この 体系は 1957 年のヴァチカン会議 (O'Conell 1958) により 5 種族に発展した。その 後の 60 年余りの努力に拘らず、現在でも各種族の正確な特性に関しては不確実さ が残っている。もっと重要なことはそれらの特性が銀河系の進化に対して何を意味 するかがはっきりしていないのである。実際、何種族が存在するか、一体はっきり 区切られた種族が今でも有効なパラダイムであるかについての合意すら存在しない (Majewski 1993, 1999)。 		これまでのシリーズ論文　

　第１論文(Reid, Majewski 1993) は写真乾板を用いて銀極方向の星の 分布を調べた。第２論文 (Reid et al 1996) は狭いが非常に深いデータを用いて ハロー光度関数に制限を加えた。第３論文(Majewski et al 1999) はここでは 議論しないスターカウントに現れた異常成分がサジタリウス矮小楕円銀河から 剥ぎ取られた星流である可能性を論じた。

各章の内容　

　今回はカプタイン選択星域のＣＣＤデータをより洗練された手法で解析する。 第２章はデータの説明、第３，４章は測光パイプラインの詳細と恒星の分類法 を述べる。次にデータの一部を用いて測光視差により、これまでの研究のどれより も強い制限を銀河系の星の分布に掛ける。第５章は測光視差の説明。第６−８章 はスターカウントの解析とモデルフィット。第９章は結果の考察。第１０章が まとめである。

　２．観測計画　

　２．１．全体　

スターカウントの基本式　

　スターカウントの統計学的基礎は von Seeliger 1989 の基礎方程式にある。 カラーも含むように拡張するとこの式は、



ここに、 A はある等級、カラーでの星の計数密度；　Ai は種族 i からのその計数への寄与； Ω は立体角；Φi は種族 i の 光度関数； Di は絶対等級 M とスペクトル型 S の関数としての 種族 i の密度分布 ? ；　r は視線に沿った距離で ある。この式は反転可能では ないのでスターカウントから成果を出すのは難しい。この結果、スターカウントは それ自体では銀河構造を探求するには不十分な道具である。ただし、外部情報と 組み合わせると、これは強力な道具に変わる。

スターカウントの解の非一意性　

　解の非一意性は表１に示される銀河構造モデルに見られるパラメターの巾に 見てとれる。薄い円盤のパラメターは狭い範囲に集中しているが、厚い円盤 （ヴァチカン会議の中間種族 II）のパラメターは図１に見るように大きく分散している。

図１．以前の研究による、厚い円盤の規格量対スケール高。Chen et al 2001 ははずれ 過ぎているので外した。点線＝厚い円盤に含まれる質量比一定の線。黒四角、黒丸＝ 過去の測光視差を用いた研究。



厚い円盤、ハローパラメターの発散　

　表１にある研究はしばしば同じ方向、例えば銀極、を調べている。そのような 研究の結果が似た値を出しているのは有望である。それにも拘らず、厚い円盤が 他からはっきり区別される種族なのか、単に古い円盤の拡張された尻尾なのか に関して現在も議論が続いている。ハローに関して述べると、スターカウント の結果はパラメター空間全てにばら撒かれていると言える。それは平坦な ドボークルール楕円体(Wyse,Gilmore 1989, Larsen 1996) からほぼ完全な べき乗則球体(Ng et al 1997) に及ぶ。

我々の観測の利点　

　多数のカプタイン選択領域で測光、分光、固有運動を測る計画の一環として 我々は画像データを取得した。これらは、例えば Chen et al 2001 が用いた SDSS よりも、測光精度が高い。我々の観測の優れている点は次の 8 点である。

（１）．観測方向の数　

　過去の研究の多くは一方向を広く(Gilmore,Reid 1983)かほんの数方向の深い 観測（論文I,II）に基づいて解析を行ってきた。多方向を目指した研究としては Basel Halo Program (Buser, Rong, Karalli 1999) が約４０年間に渡る写真乾板 によってプログラム領域を探査している。Busancon　計画 (Robin et al 1996) は 種族合成の手法で自分たちのプログラム領域と過去のデータを合わ


図２．観測領域。白四角は現在のところ R, I データが不完全。 		せて解析している。 現在までに最も広範な APS-POSS 計画(Larsen 1996)と SDSS はその第１解析結果 を Chen et al 2001 で発表した。
　論文 I と Robin et al 1996 に述べているように、一方向のみの観測だと、解の 密度則が縮退する。さらにそれが銀極方向の場合、Gilmore, Reid 1983, Gilmore 1984, Robin,Creze 1986, Yoshii,Ishida,Stobie 1987, Kuijken,Gilmore 1989, 論文I, Ng et al 1997, には種族の動径方向分布が完全に鈍くなってしまう。この論文では 表２と図２(Aitoff 投影)に示すように 11 のカプタイン選択領域 + 一つの付加領域 の観測結果を用いる。それらの領域は南銀極、銀河系反中心、銀緯 = 90° - 270 ° 銀河中心の上と下 40° 離れた方向を含む。


表２．観測フィールドの位置。

（２）．暗い星での銀河との分離　

　この観測の平均到達等級は V ∼ 22 である。この等級はこれまでの深い探査、 論文 I, Robinm Reyle, Creze 2000, Chen et al 2001, と同程度であり、広探査の Larsen 1996, Robin et al 1996, Buser 1999 よりはずっと深い。我々の観測は HDF や Franking Fields, SA57(論文 I)の深さには達していないが、それらは観測天域が狭くて 星数が足りない。Zheng et al 2001 による HST を用いた多方向観測でさえ、１ポイン ティング当たり 10 星しか検出していない。銀河カウントサーベイ(Phleps et al 2000) の画像からスターカウントを抽出することは可能だが、深くなると二つの制限が現れる。 一つは銀河 - 星の分離が難しくなる。地上望遠鏡では 22.5 等より暗い天体をはっき りと銀河か星か見分けるのは極めて困難である。V > 22 では、銀河の数が 星の数を圧倒するので、この問題はスターカウントに対して深刻である。第２の 問題はハローのパラメターに対するスターカウントの反応の鈍さである。ハローの 体積が非常に大きいので厳しい制限が付けにくいのである。このようなわけで、 深い観測は必ずしも優れた結果を産み出すわけではない。この問題の議論は 論文II と Reid et al 1998 を見よ。

（３）．測光の線形性　

　過去の研究の多くが写真乾板を用いている。表１でそうでないのは Ng et al 1997 と Chen et al 2001 だけである。写真測光の利点は一度に多くの星を観測できる ことであり、問題点はその非線形性にある。較正の誤りは直ちに密度則の変化に 反映される。その上、我々の観測の等級巾 12 ≤ V ≤ 22 の広さは、単に深い だけの観測、例えば HST では銀河系の最も離れた星しか測定できない、に較べずっと 内容が豊富である。例えば、 Gizis, Reid 1999 は HST によるハローの光度関数は 地上観測の結果と矛盾するがその原因は HST 観測が天の川の近距離成分を観測 出来ないことにあることを示した。

（４）観測領域の広さ　

スターカウント観測の重要な要素の一つは観測領域である。広くなるほど 密度揺らぎの影響を受けにくくなる。我々の観測領域は各々 1.5 - 2.5 平方度 ある。CCD 観測でこれを凌ぐのは Chen et al 2001 の　279 平方度だけである。 他の CCD 観測は 1.4 平方度 (Robin et al 2000), 0.0124 平方度 (論文 II), 0.2 平方度 (Zheng et al ) である。 		（５）．一様性　

　前に述べた困難さの多くは複数のデータセットを組み合わせることで回避される。 Robin et al 1996, Robin et al 2000 はこの方法を採った。しかし、その結果 データの非一様性によりスタ-カウント間にずれが生じるという問題が発生する。 実際、Robin らは同じフィールドのスターカウントが異なる研究間でずれている ことを述べている。我々は同じ望遠鏡の同じフィルターを使い、同じ処理を 施した。

総合点　

　個々の点では我々の観測より優れた観測があるが、先に述べた利点を総合すると、 我々の研究に比肩するのは Chen et al 2001 のみである。しかし、それでさえ 　SDSS ストリップという必ずしも密度則を得るのに最適とは言えない領域を サーベイしている。他の広域観測は APS-POSS 観測で 90 方向の計 1440 平方度を 12 > O > 20 で観測した。この観測は光電測光で測光の非線形性を補い、 深さの不足をサーベイ空間の大きさで補っている。

赤外観測　

　これまで、議論は可視域に集中していた。今後は 2MASS のような赤外全天サーベイ の解析から大きな進歩があるだろう。特に低銀緯での NIR スターカウントは有用で ある。2MASS の主な制限は比較的浅い観測限界と、K-, M-型星のカラー範囲が極端に 狭いことである。これはスペクトル型への分解度に影響する。

まとめ　

　結論として、我々の研究は近くの薄い円盤から遠くのハローに至る広い 範囲で密度則を導くに十分な深さと広さを兼ねている。また、銀緯と銀経の 組み合わせは論文 I で述べたスケール高の縮退を解くことができる。

　２．２．観測　

　1993 - 1997 の 51 晩で 12 領域の観測が行われた。望遠鏡は Las Campanas Swope 1m 望遠鏡である。CCD は　1993 - 1995 はTektronix 3, 1995 - 1996 は Tektronix 5, 1997 は SITe 1 である。測光値は Landolt 1992 システム = ジョンゾン UBV + カズンズ RI に変換された。露出時間は短時間が 15 - 40 s, 長時間が 450 - 1200 s である。その限界等級は (B, V, R, I) = (21.1, 21.4, 21.5, 20.6) である。

　３．測光パイプライン　

　３．１．整約　

　CCD 画像は ccdred により処理された。測光は DAOPHOT により行った。観測フィ ールドは混んでいないのでアパーチャ測光で十分という議論もあるが、DAOPHOT が 出力する構造パラメターは天体の分類に有用である。また、暗い天体ではアパーチャ 測光は PSF 測光より悪くなるのは良く知られている。最後に PSF 測光はバッドピク セルを越えて内挿することによりデータ精度が上がる利点もある。

　３．２．整約　

　各観測ラン毎に変換式の係数を以下のように決めた。



　ここに、 mb, mv, mr, mi は装置 等級、Xv, ... はエアマスである。解法は Harris, Fitzgerald, Reed 1981 に従った。クロスターム、二次タームの係数は小さくて落として構わないことが 判った。解は全てのバンドで 0.03 等以下の精度で収束した。

　整約の第一ステップ 　

　我々の目標は重なりあった部分を使って観測領域をモザイク化することである。 その第一ステップは各サブフィールド（フレームのことらしい）内で複数 フィルター のデータを結合して整約測光カタログにまとめることである。この装置等級サブ フィールドカタログは上の式で標準システムに変換される。各フレームの測光値は 全部の平均画像の測光値と較べられ、ゼロ点の残差が各フレームの 		v1 項に加えら れる。このプロセスが残差が指定した値になるまで逐次的に繰り返される。こうして ゼロ点の差がなくなったら等級が最終値として平均される。
これが重なりあい部分での作業なのか、あるフレームにつ いての話なのか判らない。

　整約の第二ステップ 　

　第二ステップは重なるサブフィールドの等級を比較してかみ合わせる。ゼロ点 の残差が 0.01 - 0.1 等残るが、透明度、減光等の変化の影響であろう。 多くの観測は非測光夜に行われた。それらのサブフィールドを較正するため、 我々はサブフィールドの縁の重なり合い部分の星を使い、ブートストラップ 較正を行った。直接比較から各 CCD フレームのゼロ点が計算できる。次に 非測光夜の観測フレームに対してカラタームが決められる。ブートストラップ 較正には非線形効果は認められなかった。

　Landolt 標準星との比較 　

　これらの残差が補正された後、各選択領域内の Landolt 標準星を我々の 測光値と較べた。この比較の残差は、図３に示すように、予期される測光分散の 範囲内に収まった。

恒星位置　

　恒星位置は USNO SA2.0 カタログから STSDAS TFINDER を使って決めた。次に その位置を星の同定に使って、サブフィールドカタログを結合した。測光視差 に使われた R, I データは多重観測の星の除去をしていない。その効果を 測るために立体角を．．．（ここの意味不明）


図３．Lndolt 標準星の測定値とカタログ値との差。Ｂバンドの傾きは統計的には 意味が無い。

　４．検出の完全度と分類　

　密度分布への銀河の影響　

　深いスターカウントは暗い銀河の混入の影響を強く受ける。(論文I を見よ) 我々の限界等級 R ≈ 21 では銀河の数が星の数より一桁多い。銀河の分布 は一様で暗いので、銀河除去が不十分だとハローが丸くかつ密度分布が平坦に なる。

星を銀河から区別する方法　

　論文 II に示したように測光の情報のみでは銀河から星を区別するには不十分 である。多色空間内で星の位置の 2 σ 内に銀河の約 2/3 が存在する。 結局のところ銀河は星から出来ているのだからこれはそう驚くべきことではない。 形態情報は最良の方法であり、論文 II では 4 つの方法を述べている。それらは 像の楕円率、DAOPHOT からの χ パラメター、像の集中度を表わす二つの 値、である。

ここで採用した方法　

　これは有効ではあるが、 HST や Keck で少数の天体を扱うためのものであり、 今回のようにピクセルサイズが大きい、0".61 - 0".69 / pixel、向きでない。 その上、データ量が大きいのでより自動的な手法が必要である。 DAOPHOT の 提供するパラメターは分類に十分な情報を備えている。daofind からは roundness と sharpness を、 ALLSTAR は χ と SHARP を提供する。

分類限界　

　図４は典型的フィールドにおけける形態パラメターを等級の関数として 表わしたものである。ある等級より明るければ、星と銀河ははっきりした それぞれの場所を占めている。二種類の天体の占める場所が溶けあう等級 が我々が確信を持って星と銀河を分けられる範囲を決める。それより暗い 天体の分類は潜在的に誤りを含むと看做される。 　我々の解析は分類限界より明るい側に制限されるから、我々のサーベイ の完全性を規定するのは等級限界でなく、分類限界である。勿論、ある CCD フレームに対しては両者は相関している。

この論文の分類法　

　我々の星 - 銀河分離は各サブフィールドで、等級 - χ、等級 - χ 分布 を目視して分類限界を定めることである。この等級より下の天体は、χ < 2 で、 -0.4 < SHARP < Su なら星と看做す。ここで Su は銀河と星が溶け合う等級

図４．SA 107 中心部の Sharp と χ の等級分布。各パネル上部が 銀河、Sharp = 1, χ = 0 付近が星。横線は星と銀河の分離線。 縦線は分類限界。


での Sharp 値である。Su は画像毎に 異なるが 0.1 - 0.15 である。Daofind パラメターは IRAF のデフォールトの -1 < ROUND < 1、0.2 <: SHARP < 1.0 にしたままである。この 方法は多くのテストからの結果である。


図５．縦軸＝加えた星の再生率、横軸＝星の等級 - 分類限界等級。
　　　(a) 全体　(b) 分類限界付近拡大図



　４．１．Addstar　

分類前の回収率　

　パイプラインテストの最初は addstar を用いて V = 15 - 25 に均等に分布 した 1000 個の人工星を画像内に埋め込むことである。埋め込まれたフレームを 測光、分類して人工星がどう扱われたかを調べる。図５a はこの分類が実施され る前の結果を示している。回収率は分類限界を越すまでは 100 % であり、 分類限界の 1.5 等下で 50 %、3 等下で 0 % になった。この結果は分類限界が 実際には何等であるかに拘りなく成立した。図５b は人工星の等級範囲を 分類限界を中心に 3 等の巾に制限して行ったテストの結果である。ここでは 分類限界の 1.2 等下で回収率が 50 % に落ちていることが判る。

分類後の回収率　

　続いて天体分類パイプラインを通して、何個の星が銀河と誤審されたか を調べた。図６には星としての分類保持率を等級の関数として示した。 図を見ると保持率は 90 - 100 % で、分類限界より明るい側では等級に 依らないことが判る。

人工星の PSF　

　人工星の等級測定はエラーが異常に小さい。これは使用した解析的 PSF が 綺麗過ぎたためである。図７には SHARP と χ の分布を示した。図４と較 べると違いが明らかである。

図６．縦軸＝銀河除去後に残った星の割合。(a) 全体　(b) 限界付近での計算


図７．人工星の SHARP, χ 分布。図４と較べ、散らばりが小ささい。

　４．２．Artdata　

人工銀河の追加　

　第二のパイプラインテストは artdata を用いて合成スターカウント観測を 作り出すことである。我々は、事前に決めた銀河系モデル(論文 I の暫定モデル) に従って恒星カタログを発生させた。そのサンプルにべき乗則 N(A) ∝ 100.18 m に従って 700 銀河を加えた。このべき乗則は R バンド 銀河サーベイから導かれるのより浅く（緩い？）、人工データの分類限界近くで、 適当なレベルの銀河混入を与える。ドボークルー回転楕円体と指数関数型円盤 の二種類の銀河を色々な傾斜角で加えた。このカタログは合成 BVRI 画像に 加えられ、現実的なポアソンノイズと典型的な背景スカイが乗せられた。

回収率　

　図８a は人工データに対する分類前の回収率である。全体の傾向は addstar と似ている。図８b は分類後の保持率である。データ点は分類限界の手前で 落ちている。データを調べた結果、この落下の原因はビニングにあることが 判明した。テスト結果は分類限界で 92 % である。


図８　artdata で加えた星の回収率。(a)分類前の回収率 (b)分類後の保持率
χ と Sharp 　

　図９は χ と Sharp の分布を示している。少なくとも２フレームで 607 銀河が測光され、それらの内 110 は分類限界の上であった。分類 パラメターをそれらの中の二つを除く全てを消去してしまった。その二つ とも暗いドボークルー銀河であった。

roundness と sharpness パラメター　

　我々は daofind の制限を広げることにより、事前選択パラメター、sharpness と roundness、を分類の道具として使った。sharp 限界を変えるとサンプルが 数個増えた。roundness 限界を -1:1 から -2:2 へと広げると、初めの 3000 検出天体が 176 個増えた。しかし、眼視の結果それらの殆どがノイズスパイク と数個の明るい星であることが判った。新しい検出の内,明るい星３つはパイプ ラインにより撥ねられた。これらから、roundness と sharpness パラメターは 主に宇宙線を分離する働きがあることが判る。事前選択パラメターが不適当に 星を撥ねる割合は 0.1 % 以下であり、除去された星は非常に明るい飽和した 星である。







図９．artdata による人工銀河の SHARP と χ の分布。図４と較べよ。

　４．３．ASA 184 の深い露出　

du Pont 2.3m との比較　

　最後のテストは サジタリウス流に関し(論文 III)使われた ASA 184 の深い 露出を、ハロー非対称性に制限を付けようと Swope 望遠鏡で撮った露出と 較べることである。我々は Swope 画像と du Pont 画像の双方の中に分類限界 の上にある 430 天体を同定した。次に、分解能がより高い du Pont データを 用いてこれらを分類した。

χ と Sharp 　

図１０にはこれらマッチした天体の χ と Sharp をプロットした。パイプラインは Swope 画像中で 36 銀河を正しく分類している ことが判る。一方共通の 394 星は Swope 画像中で 10 星を除いて残り全ては 正しく分類された。分類が誤った星は全てチップの縁にあるか、バッドコラムか 明るく飽和した星だった。図１１は回収率である。星の回収率は分類限界等級 で 90 - 100 %、それより 0.9 等下で 50 % である。これは人工星の場合と似て いる。

　４．４．クエーサーの混入　

クエサーは大抵星より青い　

　これまでの分類法は星と見かけが異なる銀河に有効である。しかし、クエーサー は点源である。論文 I で述べたように、これらは暗く青い領域では 25 % を


図１０．Swope 1m(左)とdu Pont 2.5m(右)での SHARP と χ の分布。
　　　　四角は銀河、黒丸は星、分類は du Pont による。 		占める。クエサーは B-V < 0.6 で、我々が扱う星はそれより赤いので 余り重大な問題ではない。それでもいくらかの混入はあり、統計的な補正が 必要である。

クエサー混入の評価　

　クエサーがスターカウントにどのくらい寄与するだろうか？Kron et al 1991 の 光度関数を、SDSS からのカラー変換式を使って評価すると、20 < R < 21, 0.4 < R - I < 0.6 の範囲のクエサー数は 1 平方度当たり 32 個となる。 色等級図ビンには 150 - 500 星を含むので、クエサーの割合は 5 - 25 % という ことになる。高銀緯ではクエサーの影響が大きい。第６章で稠密銀河の影響を 統計的に補正した場合との比較を行うが、密度則の結果に殆ど影響しないことが 判っている。それで、ここでは補正を行わない。

　４．５．系外天体の混入全般　

テストのまとめ　

　ここまで述べたテスト結果を考えると、ある等級限界より上では銀河をほぼ 100 % の効率ではじき出せるし、分類限界まででも 95 - 100 % の確率で 正しく分類できる。不完全性で失われる星よりも危険なのは潜在的等級バイアス である。しかし、我々の結果はパイプラインで回収される星の割合は分類 限界まで一定であることを示している。



図１１．Swope がぞうからの回収率分布。

　５．測光視差　

RI データで出発　

　この研究の目標は論文 I で行った仕事、複雑な銀河系構造モデルを作り モデルからの合成データとスターカウントを比較する、を拡張することである。 この論文ではもっと簡単なモデルを用いて、銀河系の密度則を初めて導く。 選択領域の７つから R, I データを取り出し、測光視差を決めて密度則に 制限をかける。 R, I データが選ばれたわけはデータの質が一様で、赤化に 比較的強いからである。将来は UBVRI データを使い、光度関数と空間分布 の双峰に制限がかかるようにしたい。

　５．１．赤化の補正　

赤化マップ　

　赤化マップは COBE/DIRBE に基づく Schlegel, Finbeiner, Davis 1998 の ものを使用する。これは以前の Burnstein, Heiles 1982 に近い。測光視差に 含まれる赤化補正量は一般には小さい。大部分の領域で EB-V ≤ 0.05 であり、最大でも SA95 の EB-V = 0.1 である。ここでは 扱わないプログラム領域の幾つかはもっと大きい赤化を示す。 SA 95 では 領域に渡って微分赤化の証拠が 		見られる。そこで、Schlegel et al 1998 を 内挿して各星の位置ごとに赤化を与えて補正した。赤化係数には Landolt UBVRI システムのものを Schlegel et al から採用した。

青い縁　

　図１２の青い縁は主系列ターンオフを表わしている。以前の研究、Unavane, Wyse, Gilmore 1996, Chen et al 2001、で青い縁のカラーは等級の関数として様々な (l, b) で一定であることが示された。従って、このカラーは赤化を調べるよい 指標となる。 この後に出る論文 V ではこの補正の正しさを示す。SA 95 の 青い縁ははっきりしない青い帯から青い狭い線に変わった。

吸収物質は手前か？　

　ここではダスト吸収は全て対象星の手前で起きると仮定した。これは特に 銀河面に近い星では不適当である。それにもかかわらず、大部分の星に対しては それでよい。というのは、赤化物質のスケール高は 100 pc 程度 (Chen et al 1999) であり、この値は古い円盤、厚い円盤、ハローの星の距離に較べるとずっと 小さいからである。


図１２．(a) SA107　矢印はMSTO (b) SA95 赤化変動激しい領域 (c) SA95 赤化補正後。　深さも分散もSA107の方がよい。

　５．２．MR - (R - I) 関係　

ヒッパルコス近傍星　

　測光視差を決める最初のステップは絶対等級を決めることである。 我々は観測される星は矮星であると初めから仮定し、(R - I) と MR の関係を導いた。その関係を導くにはヒッパルコスカタログと、Bessell 1990, Leggett 1992 の測光を用いた。それらから、既知の連星、視差の精度が低い 星(σ&pi+/π > 0.2)、明らかに主系列から外れている星 を除いた。Lutz - Kelker 補正(1973) を施した後に次の式でデータをフィット した。

　　MR = -6.862 + 61.375(R - I) - 108.875(R - I)2
　　　　　+ 90.198(R - I)3 - 27.468(R - I)4
　　　　　　　　0.4 ≤ R - I < 1.0 230星より

　　MR = -114.355 + 408.842(R - I) - 513.008(R - I)2
　　　　　+ 286.537(R - I)3 - 59.548(R - I)4
　　　　　　　　1.0 ≤ R - I < 1.5 　195星より

フィットの結果は図１３に示した。つなぎ目の R - I = 1.0 で 0.1 等の段差 が生じた。 R - I = 0.4 でフィットをやめたのは主系列ターンオフのために 測光視差の不確定性が大きいからである。

測光視差の誤差　

　カラー対測光視差関係は 0.2 - 0.3 等の不定性がある。したがって、ある 特定の星への距離には或る程度の誤差が含まれる。この分散がランダムな 距離エラーを生むならば 70,000 星の統計解析にはあまり影響しない。しかし、 マルキストバイアスの効果により系統誤差が生まれる。


図１３．ヒッパルコスカタログの MR - (R - I) 関係。
　　　　実線は我々のフィット。上の系列は連星なので無視。下のエラーバー
　　　　付きデータは準矮星。古い銀河種族のターンオフが、我々が密度則を
　　　　導くのに使う R-I > 0.4 よりずっと青いことに注意。

　５．３．マルムキストバイアス　

バイアスの補正式　

　みかけ等級で制限される円錐では、固有光度が明るい星の距離は 暗い星より大きい。この効果はマルキストバイアスと呼ばれ、その効果は次の 式で表わされる：

M(R) = Mo - σ2 dlog A(R)
0.4343 dR
エラーは次の式で与えられる：

σ2 = dM(R-I) σR-I2 + σM(R)2
d(R-I)
ここに、Mo は (R-I) - MR 関係 MR = f(R-I)から導い た絶対等級、A(R) は見かけ等級 R における微分カウント、 σR-I は MR = f(R-I) 式から伝播してきた等級 エラー、σM(R) は内在的な固有の分散である。

個々の星にはこの補正は要らないこと　

　上の絶対等級補正は星の統計的な評価にのみ適用されるのであって、個々の 天体として扱う際にはこの補正は不要である。この操作は σπ /π 限界のサンプルを Lutz-Kelker 補正するのと似ている。

補正手続き　

　マルムキスト補正を行うため、各フィールドのヘス図を作った。この図を カラーで 0.1 等、等級で 0.5 等の区画に分けた。暗い等級の区画は対応する 深さに完全なサブフィールドの数の減少を反映するように補正された。
何だ、これ？　暗くなると探査体積が小さくなること の補正じゃないらしい。
各カラー区画で A(R) 関数は多項式でフィットされた。フィットの係数は カラーに従って滑らかに変化した。これは、カラー - 等級 - カウント曲面 が適性に表現されていることを示す。各カラーで微分係数が評価され、 カラーエラーと結合されて MR = f(R-I) 関係の固有分散が 求められ、絶対等級の補正が導かれる。

マルムキストバイアスの効き方　

　最も遠い星はマルムキストバイアスの影響は最も受けない。なぜなら、この 微かな等級では微分カウントが R-3 密度則から判るように平らに なってしまうからである。その結果、微分カウントの微係数がゼロになり、 補正が最小になるのである。近傍の星は傾きが急なため補正は大きくなる。

　５．４．準巨星の混入　

「厚い円盤」は準巨星と巨星を見誤ったのか？　

　測光視差では全ての星が矮星と仮定している。準巨星と巨星の数は矮星より 一桁少ないが明るいので検出体積が大きいので、光度関数で見るよりスターカウ ントへの影響は大きい。Bahcall, Soneira 1984 は、Gilmore, Reid 1983 が「厚い 円盤」としたのは準巨星を見誤ったのだとした。この議論は論文 I で批判された。 しかし、準巨星の混入はきちんと評価される必要がある。

準巨星のスターカウントを見積もる。　

準巨星の数　

　等級間隔 (m - δm, m + δm) に混入する巨星/準巨星の数 NSG を求めよう。見かけ等級 m に対応する準巨星距離は、 rSG = 10(m - MSG + 5)/5 なので、

NSG = Ω κSG,D ∫ rSG+δr(SG) ρ(rSG)rSG 2drSG
rSG-δr(SG)


ここに、κSG,D は準巨星と矮星の存在比、ρ は矮星の密度で ある。この式は基本的には von Seeliger 式である。区間内で密度がほぼ一定の 時に上式は、

　　　　　　　NSG = ΩκSG,Dρ(rSG) × 2rSG2δr(SG)

となる。

矮星の区間体積　

　同じ等級区間(m - δm, m + δm) に対する矮星の距離区間は (rD - δrD, rD + δrD) である。この体積は VD = 2ΩrD2δ rD となる。

準巨星の密度への寄与　

準巨星 NSG がこの矮星体積の中にあると 看做してしまうので、準巨星による星密度への貢献分は、
ρSG = NSG = κSG,DrSG 2δrSGρ(rSG)
VD rD2δrD



準巨星密度寄与の評価　

　　　　　rSG = rD√(LSG/LD), 　　　　　δrSG = δrD√(LSG /LD)

なので、先の式に代入して

ρSG = ( LSG ) 1.5 κSG,D ρ [ rD √( LSG )]
LD LD


κSG,D と (LSG/LD) を一定とした時、 準巨星の大きな光度に由来する大きな区間体積は正にその大きな光度のための 遠方での低い密度により相殺されてしまう。特に、密度低下が r-3 より急な場合にそうである。我々のフィールドは多くの場合、方向ベクトルが 銀河系からの動径ベクトルと平行である。動径ベクトルに沿って, 遠方では R-3 である。SA 107/SA 184 領域は銀河系内側を向いて いるので、距離 5 から 10 kpc までは密度が増加するので準巨星の寄与が 他より大きい。

混入率の評価　

　κSG,D と (LSG/LD) はカラーに より変化する。カラーが非常に赤いところでは、κSG,D が 小さく、 (LSG/LD) が大きい。そこで、 準巨星/巨星の混入は最小に抑えられる。
ここの理屈が理解できない。
晩期 G-, 早期 K-型星では混入効果はより大きくなる。 ここでは、混入効果を最も青く明るい、5.8 ≤ MR、矮星で評価 しよう。まず、Bergbusch, VandenBerg 2001 の等時線から κSG,D と (LSG/LD) を評価する。
　　　遠方ハロー星に対しては [Fe/H] = -1.5, t = 16 Gyr,
　　　厚い円盤と古い円盤に関しては　 [Fe/H] = -0.6, t = 12 Gyr で
　　　　　LSG/LD ∼ 26, κSG,D ∼ 0.03
を得た。この値を上の式に代入すると、
　　　ρSG = 261.5×0.03×ρ(26 1/2rD) = 4ρ(5rD)
準巨星混入の最悪のケースである SA 184/SA 107 方向でも、この効果は無視 できるほどであった。したがって、この先では準巨星/巨星は無視する。

　５．５．準矮星　

低メタル星の主系列　

　前に述べたカラー等級関係は太陽近傍の高メタル星のものであった。低メタル 星ではラインブランケッティング効果が変化するためこの関係も変わる。 同じ質量同士で較べると高メタル星は一般に赤く暗い。R バンドで見ると、 G-型星ではラインブランケッティング効果が小さいが、 K-,M-矮星になると TiO, VO 線のため高メタルでは強い吸収帯が発生する。結果として、低メタル星 の主系列は青側にずれる。その結果、カラーから測光視差を決めると低メタル星 は系統的に遠い側に置かれることになる。もし、平均メタル量が場所により 変化すると、このメタル量効果を考慮しないと空間構造に系統誤差が導きこま れることとなる。

低メタル星のカラー等級関係　

　低メタル星のカラー等級関係を導く作業は、正確な三角視差と測光値の揃った データが少ないため困難に直面している。そこで、Gizis, Reid 1999 の戦略を 採用した。５．２．章で与えた関係は太陽近傍の [Fe/H] = -0.2 のサンプルに 対するものであった。Gizis 1997 の低メタル星サンプルに対しては

　　MR = 2.03 + 10.0 × (R-I) - 2.21 × (R-I)2

を得た。Lutz-Kelker 補正は施している。この二次式は Gizis, Reid 1999 の 二本の一次式による表現を合致している。与えられたメタル量とカラーに対し、 その絶対等級は上に与えた二つの表式の間を線形補完することで得られる。



図１４．準矮星への補正。実線は太陽メタルＨＲ図。鎖線は [Fe/H] = -1.2 に対し我々が導いたＨＲ図。一点鎖線は Gizis, Reid 1999 が導いた準矮星 "sd", [Fe/H] = -1.2, と極端準矮星"esd", [Fe/H] = -2.0 のＨＲ図。長鎖線は Bergbusch, VandenBerg 2001 の [Fe/H] = -1.14 等時線。三角([Fe/H]=-2.0)、 ダイヤ([Fe/H]=-1.2) は三角視差のある Gizis 1997 の Lutz - Kelker 補正後の 準矮星データ。

メタル量の決定　

　Gilmore, Reid 1983 に倣い、星のメタル量は銀河系内の位置で決まるものと する。 K-巨星の平均メタル量をその場所での平均メタル量と考え、 Yoss, Neese, Hartkopf 1987 の垂直方向メタル量勾配を少し変えて、

0 < z < 0.7 kpc [Fe/H] = -0.4z
0.7 < z < 7.5 kpc [Fe/H] = -0.28 - 0.18(z-0.7kpc)
7.5 kpc < z [Fe/H] = -1.5
初めの二つのメタル勾配は Yoss et al 1987 からそのまま持ってきたが、 彼らと違いメタル量が -1.5 に達したところで止めてある。この値がハロー の平均メタル量, Garney et al 1996, だからである。

　Trefzger, Pel, Gabi 1995 も経験的なメタル勾配を出しているが、この モデルはメタルの動径変化を説明しない。ハローの垂直メタル勾配は否定 され、Searle, Zinn 1978, Carney et al 1990、厚い円盤にメタル勾配がある かどうかは、Rong et al 2001, Gilmore,Wyse,Jones 1995, Reid 1996、議論が 分かれている。これらの研究は各種族を分離し、それぞれのメタル分布を独立に 決めている。しかし、これは危険なやり方である。なぜなら、重なり合っている 星種族を分けるのは困難であるし、見かけ上のメタル量勾配は夫々が一定メタ ル量の二つの種族の境界領域での重なり合い効果かも知れないからである。しか しながら、我々の改訂版メタル勾配をモデルのメタル量分布から導かれる勾配に 較べてみることにしよう。

メタル量勾配の比較　

　第７章で導く密度則に、伝統的な仮定、円盤、厚い円盤、ハローの平均メタ ル量は [Fe/H] = 0.0, -0.6, -1.5 を組み合わせると、厚い円盤 に対応する高度 2 - 6 kpc 付近で、Yoss 勾配は少し(∼ 0.1 - 0.2 dex) メタルが高すぎることが判る。第２式の勾配0.21 dex / kpc はモデル勾配に よりよく合う。結果が似たようなものなので単純さを優先し経験的 メタル量勾配を維持する。

距離決定　

　各星に対し、太陽メタル量を仮定した予備的距離が計算される。次に、その 距離で決まる高度に対してメタル量を決め直す。そして、内挿法で絶対等級を 求める。この過程を距離が 5 pc 以内に収束するまで逐次近似する。



図１５．SA101 でのマルムキストバイアス、準矮星バイアス、銀河除去の効果。
　　　銀河除去は密度則を大きく変えるがマルムキスト、準巨星効果は小さい。



エラーの影響　

　注意しておくが、準巨星補正に含まれる系統エラーは密度則の系統エラーに 反映される。例えば、遠方星のメタル量を系統的に低く評価すると、絶対等級 を暗くし、距離を系統的に短くし、密度勾配を急に、スケール高を短くする。 この点の議論は第８章で行う。図１５にエラーの影響をまとめた。

　５．６．連星　　

連星入りのサンプルを使ったシミュレーション　

　銀河系種族 I では G-型で 50 %, K-, M-型矮星で 30 - 35 % の割合で連星で ある。連星の効果は二つある：光度が上がり、カラーが変わる。前者は星を近づ け、後者は星の組み合わせで色々な効果を生む。連星の効果を入れた密度解析を シミュレートしてみよう。

　MR = f(R-I) を仮定しておき、次のような条件でサンプル星を 作る：カラーをその関係（どの関係か不明。） から選び、 R-I と MR にガウス型分散を施し、密度分布を 300 pc 指数型密度則に従って分布させる。

　一部のサンプル星に適当な仮定に従った副星を加える。出来たサンプルを 解析し直した。図１６はその結果である。連星の質量比の分布は大きな影響を 持たないこと。連星が入ったサンプルを連星が無いものとして解析すると 密度勾配を急に見積もることがわかる。

連星率　

　この連星効果は当然のことだが、連星比率に依存する。連星率がスペクトル 型により変わるのか、ハローと厚い円盤での比率がいくらなのかについての 結論は出ていない。簡単のため、この論文では連星なしで解析を進め、最後に 連星率 50 % の補正を加える。



図１６．連星効果のシミュレーション。等マス連星とランダム質量比連星 の割り合いをパネル毎に変えてある。実線が実際の密度則。点線が連星を 考慮しないで導いた密度則。どれも密度勾配が急になることを注意せよ。

　６．解析方法　


　６．１．仮定する密度則の形　

円盤　

　銀河系の星種族空間分布を表現するために幾つかの標準的な関数形が 使用されてきた。詳しくは論文 I にある。ここでは簡単に紹介すると、

　円盤は円筒座標系で円盤動径方向と軸方向に分けて表わされた：

　　　　　ρ(z, r) = ρ0e-z/Zoe-r/Ro

似たような形だが、次のような式も使われる。

　　　　　ρ(z, r) = ρ0sech2(-z/2Zo)e-r/Ro

この形だと、z = 0 が特異点になることを避けられ、等温シートの密度勾配として 妥当であり、遠方で観測に合う。しかし、スターカウントは何十年も指数関数の方を優先してきた。 sech2 形式の方が論理的に優れているように見え、実際横向き銀河 のプロファイルはこの形でフィットされてきたのだが、最近の研究は横向き 銀河の観測プロファイルが尖っていて指数型の方が却ってよく合うという 証拠が集まってきた。加えて、Hammersley et al 1999 は赤外スターカウント の結果が、特異点の問題があるに拘らず、指数関数型の方がずっと良く合う ことを示した。もっとも、Gould, Bahcall, Flynn 1996 は反対の結果を 可視データから導いた。ここでは双方共に取り上げる。

楕円体　

　色々な式が使われているが、最も有名なのはドボークルー回転楕円体(1948) である。これを Young 1976 の式で表わすと

　　　　ρ(Rg) = ρ0exp[-7.669(Rg/ Re)1/4]/(Rg/Re)0.875

ここに Re は半値光度半径、Rgは球座標系での中心 距離である。この形式は Rg/Re > 0.2 で有効である。 我々の場合 Re < 30 kpc であれば妥当となる。 どういう意味？

　他のモデルはべき乗型の密度則を用いる：

ρ(Rg) = ρ0 1
a0n + Rgn


ここに、a0 はコア半径である。この量はしばしば無視される。べき乗則 は冷たいダークマター（CDM) モデルが予言する分布則に近い。

CDM モデル　

CDM の予言する分布はもう少し複雑で、

ρ(Rg) = ρ0 1
(Rg/Rs)(1 + Rg/Rs) 2


ここに、Rs はスケール半径である。この密度則は内側の勾配が 外側より緩くなる点で単純なべき乗則と違う。注意すべきは星のハローと ダークマターハローが同じ構造を取る必然性はないことである。ハロー星の 運動を説明するためにはダークハローは星のハローより浅く(R-2) 重くなければならない。このように、CDM による定式化はスターカウントに 関してはやや疑問である。

　回転楕円体定式化では Rg は真の銀河中心距離ではない。これは 軸比 (c/a) により次のように補正される。

　　　　　Rg2 = {r2 + [z(c/a)]2} 1/2

　バルジ　

　我々の解析ではバルジ回転楕円体の分布式は重要でない。我々は低銀緯での 第１、第４象限のデータを欠いているのでバルジに制約をかけられない。そこで 文献にある Rg-3 分布則を太陽近傍で 0.02 % に規格化 して用いる。

ハロー　

　ハローに関してはスターカウントのような粗い方法ではドボークルー則と べき乗則の違いは問題にならない。ここでは両方を使うことにする。
　厚い円盤とハローの密度規格化は薄い円盤の太陽近傍密度を基準に与えられる。 ここでやや混乱するのは文献によって、太陽近傍全ての星に対する割合か、 薄い円盤種族に対する割合かが異なることである。ここでは後者の方を採用する。

　太陽近傍に対する規格化は太陽の位置が銀河系中心から離れ、銀河面中心から やや浮き上がっていることを自然に説明できなければならない。我々は銀河中心 から 8 kpc (Reid 1993), 銀河面中心から 15 pc (Yamagata, Yoshii 1992, Ng et al 1997) という値を採用する。 15 pc は Humphreys, Larsen 1995 の モデルで薄い円盤のスケール高を 250 - 300 pc とした時と一致する。また我々の スターカウントで χ2 最小となる場合とも合致する。

　６．２．パラメター空間を探査する。　

銀河系密度分布の決定法　

　測光視差の使用により空間密度分布を直接探ることが可能となった。そこで、 これまでのようにカラー - 等級 空間内で銀河系構造のパラメターを探す代わりに、 観測値を銀河系内の色々な点における空間密度にしてしまう。これにより、密度の 測定から幾つかの方向に沿った密度分布を同時に一つの密度距離関係に直すことが できる。こうして、我々は銀河系 r - z 面内の密度分布をフィットするのである。 フィットの良さは χ2 で測る。

χ2 最小の探し方　

　 χ2 最小を探すのは意外に難しいことが判った。単純なグリッド 探査は局所的な穴に引っかかってしまう。色々試した結果、直接法に辿りついた：

種族パラメターをありそうな範囲で変えて、何百万の密度則の組み合わせを作り、 ７つの方向のデータと較べて χ2 を計算する。こうして見つかった 粗い分解での極小の周りをもう少し分解能を上げて再計算し、さらに細かく していく。こうして最終解を見つけた。

　６．３．サンプルのビニング　

密度分布と光度関数が相互に関係する。　

　我々の方法で心配なのは von Seeliger 方程式は分布関数と光度関数の コンボリューションであって、その二つは互いに無関係ではないということで ある。光度関数は場所によって変化し得るし、一方密度分布もスペクトルタイプ 毎に変わり得る。例えば、若い星は古い星より縦方向に高度が限られている。こう して、問題は単に二次元、距離対密度、というだけでなく、三次元、距離 - 密度 - 光度の関係となった。 		モデル星の分別　

　洗練されたモデル, Robin, Creze 1986, 論文 I, ではこのコンボリューション 効果をシミュレーションに取り入れている。別のやり方は、データを類似の星 同士でまとめることである。理想的には同じ質量の星を集めたいが、絶対等級 で我慢する。我々は 5.8 ≤ MR ≤ 10.2 を扱う。これは 太陽メタル量では、6.3 ≤ MV ≤ 12 または、スペクトル型 K0 から M4 の範囲である。

　６．４．収束とパラメターの漂流　

ハローパラメターの漂流　

　パラメター空間内の探索は二つの円盤種族に対しては容易に最小点に辿りつく ことが判った。しかしハローに対してはパラメターが発散してパラメター空間の 端まで行ってしまう。べき乗ハローの場合、低いべき乗指数、小さい軸比、高い 規格化値（1.0, 0.3, 0.006）へ行く。ドボークルーハローでは低い軸比 0.3, 大きな有効半径 10 kpc, 高い規格化値 0.005 である。ハローパラメターが 漂流するに伴い、二次効果として薄い円盤、厚い円盤はスケール高が 150 pc, 500 pc と平ぺったくなる。

なんか変。　

　これらの結果が正しい可能性はある。我々のモデルは種族に対して事前の 仮定を設けず、データに一番合うモデルを探している。しかし、おそらく やり方に何か欠陥があるのであろう。

ハローが複雑な構造を持っているのか？　

　この発散の説明として、スターカウントがハローパラメターに対し鈍い 点が指摘される。測光視差が粗いことがそれを増幅する。もしかすると、ハロー は方向毎に変化を見せるような複雑な構造を持っているのかも知れない。我々の サーベイは感度と完全性において優れ、ハローの副構造が解析に影響する ようになったのだろうか？

　７．ベストフィット標準モデル　



図１７．我々の最も青い星の密度等高線（実線）を論文 I （破線）と比較。
　　　　銀南極方向は合うが、銀河中心方向でモデル値が大きすぎる。
　　　　密度単位は log (stars pc-3)。記号は クロス=-3, 星=-4,
　　　　ダイヤ=-4.5, 三角=-5, 四角=-5.5, クロス=-6

　７．１．制限付きハローと円盤モデル　

仕方なくハローを固定してフィットする。　

　制約なしのハローが失敗したので、ハローの方を固定することにした。次に 厚い円盤と薄い円盤のパラメターをベストフィットさせた。結果は表３にまとめた。 球対称ハロー（Ng et al 1997, Buser et al 1999）に対してはフィットが悪い。

論文 I、Besancon I ハロー 　

　図１７では、データ中最も明るい 5.8 ≤ MR < 6.8 グループ の等密度点を論文 I の暫定モデルと比較した。これら明るい星は最も遠方まで 検出されるので、ハローに最大のてこが掛かっている。 図１７を見てすぐ分かるのは、南銀極方向は良く合い、Rg > 5 kpc もまあまあ良いが、銀河中心方向の SA 107/SA 184 での遠方ビンが過予想に なっている。同様の傾向は Besancon I ハローモデルについても当てはまる。

Larsen 1996、Besancon II ハロー 　

　フィットが最良なのは Larsen 1996 の平坦ドボークルーハローか、Besancon II の平坦べき乗ハロー の場合である。両者の予想値はほぼ同じである。どちらも 低スケール高、大規格値の厚い円盤を予想している。表４には４つの絶対等級 ビン全てに対するベストフィットを、Besancon II ハロー + 指数型円盤について、 表５では sech2 円盤モデルについて与えた。表 3 - 5 は連星効果の 補正はされていない。エラーバーは χ2 = min(χ2) + 1 で決めた。円盤スケール高エラーバーの非対称は急な密度勾配は蹴られ、緩い 方は認められたためである。 χ2 = 2.5 - 3.0 の区間には軸比 0.5 - 0.7、べき指数 2.5 - 3.5 のべき乗ハローモデルが含まれる。そのような ハローにフィットする厚い円盤は Z0 = 700 - 900 pc, R0 = 3000 - 5000 pc, ρ = 6 % - 10 % を持つ。面白いことに 絶対等級が最も低いグループは厚い円盤スケール高が他よりずっと大きい。これは 本当に暗くなるとスケール高が伸びるのかも知れないし、連星の比率が低く なるためかも知れない。


図１８．Besancon II ハロー を用いた等密度点の比較。太陽近傍に対して一致が良い。 銀河中心方向で過予想、銀河系外側は未予想。




図１９．Larsen 1996 モデルとの比較。太陽近傍に対して一致が良い。 銀河中心方向で過予想、銀河系外側は未予想。図１８とよく似ている。



ベストフィットモデルの性質 　

　図１８、１９は先に述べた二つのモデルと観測密度値との比較である。太陽近 傍に対して一致が良い。銀河中心方向で過予想、銀河系外側は未予想。ずれが系統 的であることは、まだモデルに改良の余地があることを示している。






表３．色々なハローモデルに対する指数型円盤フィットの結果


表４，平坦ハローに対する指数型円盤ベストフィット


表５，平坦ハローに対する sech2 円盤ベストフィット


表５，平坦ハローに対する sech2 円盤ベストフィット


　７．２．銀河系の形　

新しいモデルのパラメター　

　表６は新しいモデルのパラメターである。パラメターはいくつかの絶対等級区分で 求めた表３−５のベストフィットの値から合成したもので、パラメター空間の中で χ2 = 2.5 - 3.0 の範囲を反映している。載せたパラメターは 青い星に重みを置いていて暗い星に現れた薄い円盤スケール高の増大は無視して いる。表には、連星効果を入れていない場合と 50 % 連星とした場合の二つの値 が載せてある。

薄い円盤のスケール高　

　標準モデルの薄い円盤スケール高 (325 pc) より低い値が最近の多くの研究から 示唆されている。例外は Chen et al 2001 である。我々は単一の古い種族だけで 薄い円盤をパラメター化したが、これは単純化し過ぎであろう。Ng et al 1997 は 薄い円盤を３種族で記述している。しかし、我々の円盤面付近のデータは粗すぎる ので１種族以上を扱うのは無理である。その上、暗い星は古い種族が支配的（論文 I ） である。sech2 モデルのスケール高は銀河系を横向き銀河の中では 薄い円盤を持つ銀河にする(de Grijs 1998)。

薄い円盤のスケール長　

　我々の円盤スケール長 2.25 kpc は標準モデルの値 3 - 4 kpc より短いが、 エラーバーを考えるとより長い値の Robin et al 1996, Larsen 1996, Buser et al 1999 と重なる。薄い円盤の短いスケール長は赤外スターカウント ( Ruphy et al 1996, Drimmel, Spergel 2001) からも示されている。横向き銀河からは R0/Z0 の平均値として、ただし Z0 の定義は 少し違っているが、5.9 ± 0.4 を与える(deGrijs, vander Kruit 1996)。 軸比はハッブルタイプに依存し(de Grijs 1998)、銀河系の軸比 ∼ 4 は この銀河を Sc 銀河に位置付ける。

厚い円盤のスケール高　

　厚い円盤のスケール高は Chen et al 2001, Robin et al 1996 と似ている。 ただ、Robin et al 1996 にくらべ規格値はずっと大きい。規格値を他の研究と 比較するのは困難である。というのは、幾つかの研究では厚い円盤とハローの 規格化が何に対してなされているのかが曖昧だからである。我々と Chen et al 2001 の規格化は古い円盤にのみ行われているから、円盤若い種族を無視したため に規格値を大きく見積もったかもしれない。ただ、我々の研究では若い種族の 貢献は小さいのだが。Ng et al 1997 の３成分円盤の結果に基づくと、規格値は 4 - 6 % くらいかも知れない。

　論文 I、Gilmore, Reid 1983 その他で与えられている厚い円盤の大きなスケール 高は銀極方向のみを測り、それに球対称的なハローモデルを適用した結果であろう。 平坦ハローと縮退への懸念がこの研究の出発である。 SA 141 方向は 1.5 kpc の スケール高、2 % の規格値を持つ厚い円盤で図１７に見るような満足なフィット が得られる。非極方向のフィールドデータはもっと高質量の厚い円盤を要求する。

縦方向速度分散 σW　

　フィールド星の空間分布はそれらの力学を反映している。自己無矛盾な力学銀河 系はこの双方を同時に満たさなくてないけない。厚い円盤の σW は約 40 km/s (Norris 1986, Sandage 1987, Sandage, Fouts 1987, Carney, Latham, Laird 1989, Beers, Sommer-Larsen 1995, Guo 1995, Reid, Hawley, Gizis 1995, Ojha et al 1996, Chiba, Beers 2000) である。これはス




ケール高 1 kpc に対応する。かつこの 高い σW 種族は規格値 10 % である (Sandage,Fouts 1987, Sandage 1987, Casertano,Ratnatunga,Bahcall 1990, Reid et al 1995)。ただし、 Guo 1995 は 3 % の規格値を主張した。これらの研究が与えた厚い円盤のスケール高 1 kpc は我々の結果と大体一致するが、それはまた、これまでのどの研究とも大体は 合っている。高い σW 成分を持つ星の割合が 10 % という高い 値を持つモデルは我々以外に Robin et al 1996, Chew et al 2001 である。最後 に Majewski 1992, Guo 1995 は厚い円盤の運動が Z = 4.5 - 5.5 kpc まで 支配的であると主張している。我々のモデルでは密度分布がやはり同じくらいの 高さまで支配的である。

厚い円盤のスケール長　

　我々の求めた厚い円盤のスケール長は以前のスターカウントの結果と同じくらい であり、Chiba, Beers 2000 の運動学的な値とも大体合う。その正確な値より 大事なことは、厚い円盤のスケール長が薄い円盤のスケール長より大きいことで ある。これまでの研究では二つの値が等しいか、ほぼ同じであると仮定されてきた。 ただし、スケール長のエラーバーが大きすぎてこの結果を確定するに至らない。 例外は Larsen 1996 で 5 σ レベルではっきりと厚い円盤のスケール長の 方が長いという結果を出している。加えて、横向き銀河のいくつかでスケール 高が距離により変化していて、厚い円盤のスケール長が薄い円盤より大きいこと を示唆している。

　８．より複雑な密度分布へ　

フィットが失敗したわけ　

　我々が標準的な密度則でスターカウントをフィットできなかったのかには幾つかの の理由がある。それは大きく分けて、解析の問題と密度則の問題の二つである。

（１）解析法の失敗　

準矮星？　

　我々の解析はまずい準矮星の補正で傷つけられているかも知れない。これは 系統的な効果を生む。我々の単純なメタル量補正は準矮星の視差データに上手く フィットしたが測光と視差の両方が良い星の数は少なく、分散は大きい。低メタ ル星の高精度の視差と多色測光が必要である。しかし、図１４は晩期型矮星では 準矮星補正が大きいが、早期 K-型、つまりハローまで届く唯一の星グループ ではこの補正が小さいことを示している。準矮星補正が大きく間違っていない 限り、これが不一致の原因とは思えない。

　その上、青い準矮星の小さな補正はそれ自身低メタル量では一定値に漸近して いく。したがってハロー種族は [Fe/H] = -1.5 の星の絶対等級と同じくらいに なる。この「ギロチン効果」は Sandage 1969 の UV 超過の研究以来知られて いた。我々はこの効果を実証するほど多くの例がない。また、図１４の 赤い [Fe/H] = -2.0 星の分散はこの効果を決めるのに注意がいることを示す。 それにも拘らず、明るい青い星でのギロチン効果の可能性は、ある程度まで ハローの低金属星の準矮星補正のエラーの危険性を和らげる。　　　　　　　　　　　　　　　　　　　　　　　　

メタル量勾配　

　準矮星問題と関連するが、メタル量勾配が違っている可能性もある。 Yoss et al メタル量勾配はハローでは厳しく制限されていない。一般には ハローの典型的な値として [Fe/H] ∼ -1.5 が合意されているが、ハロー 星のメタル分散は大きく、メタル量副構造を持っている可能性もある。( Carney et al 1996, King 1997) それに加えて、我々のモデルには メタルの円盤垂直方向の変化は入れているが、動径方向変化は考慮されてい ない。これは単純化のし過ぎである。ただ、銀河中心方向にメタル量を増 やすと、系統バイアスがかかり我々のモデルで銀河中心方向に超過密度評価 したのと反対の効果を産み出す。その上、動径方向のメタル量勾配は薄い円盤 でのみ検出されている（Rong et al 2001）。この種族は我々の最も遠い星では 最小限にしか代表されていない。メタル量分散または副構造は第一次系統的 効果を導き出さない。

銀河分離　

　エラーの最後の原因は銀河分離を熱心にやり過ぎることであろう。暗い等級 での星の χ や SHARP 領域が広がるので暗い星は区分線により誤分類される 可能性がある。この様な問題は暗い等級で密度を一様に過大予想する結果に なる。観測されているような、方向によって過大予想になったり過小予想にな ったりすることはない。






（２）密度則が単純過ぎた？　

厚い円盤のフレアリング　

　モデルは熱い円盤のスケール高が一定であると仮定した。この仮定は銀河系の 一部、主に反中心方向でしかチェックされていない。しかし、スケール高が 銀河中心距離と共に増加する可能性はある。これは、 SA 107/ SA 184 方向の 密度超過予想を緩和するだろう。

　他の５領域は平面距離の点ではあまり広い範囲に渡っていない。そこで、SA 107/ SA 184 方向を除いて厚い円盤のスケール高を評価すると、 0.8 - 1.2 kpc となった。この値は採用するハローモデルに大きく影響される。

　上の結果は太陽近傍のスケール高は銀河系内側に較べ大きいことを意味する のかも知れない。別の考え方では、厚い円盤の動径方向密度分布は指数関数的 でないのかも知れない。局所的には指数関数的円盤であるが、銀河系内側部では より浅い密度勾配を持つ厚い円盤もまた、内側銀河系の等密度線を固定する。

三軸不等性　

　Larsen. Humphreys 1996 は APS-POSS のスターカウントに基づき、三軸不等 ハローを支持した。彼らが不等性を検出した低銀緯域は今回の研究に含まれない ので、その正否を決することはできない。SA 107/SA 184 方向は不等性の影響が 小さいので、この仮説ではその方向へのモデルの超過密度予想を説明することは できない。

複雑なハロー　

　どうもハローの単純なモデルは不十分ではないかという証拠が多い。巨星か 明るいハロー星を使った研究では球対称な R-3 則、論文 I, Ng et al 1997, Majewski et al 2000, Morrison, Borosonm Harding 2000, Majewski et al 2002、が導かれた。かなり近傍の主系列星 Larsen, Humphreys 1994, Robin et al 1996, Larsen 1996, Robin et al 2000, Chen et al 2001, や マイクロレンズ Samurovic et al 1999 を用いた研究は平坦ハローを支持して いる。幾つかの研究は軸比 c/a が一定というのは厳し過ぎ、比が半径と共に 増加するハローを使わないと RR Lyr/ HBS (Hartwick 1987. Preston, Shectman, Beers 1991, Kinmanm Suntzeff, Kraft 1994, Layden 1993, 1995, Wetterer, MacGraw 1996, Sluis, Arnold 1998)、球状星団(Zinn 1993)、 主系列星(Gilmore, Reid, Hewett 1985) の分布説明が困難であるとした。

ハローの２副種族　

　フィールド星と球状星団の運動と組成の研究は、ハローが二つの副種族から なっていることを示した。一つは平坦な内側副種族でメタル量勾配は持たず、 速度は非等方分布を示す。Zinn 1993, Dinescu, Girard, van Altena 1999。 固有運動（Carney et al 1996）やメタル量(Sommer-Larsen, Zhen 1990、 Allen, Poveda, Schuster 1991, Chiba, Beers 2000) で選ばれたハローフィー ルド星は同様の特徴を示す。もう一つは丸い R-3 成分でこちらも メタル勾配を欠く。この描像は詳細なメタル量解析に基づくハロー星組成の 二分性（Nissen, Schster 1997）からも支持される。

　スターカウントはこれまでこの可能性を無視してきた。このような可能性は スターカウントに起きた多くの矛盾を解消する。二重ハローモデルでは近傍の ハロー星(Robin et al 1996, Larsen 1996, Chen et al 2001)は平坦内側ハロー 種族に属し、遠いハロー星は(論文 I, Ng et al 1997)球状の外側ハロー種族 が支配的である。

　しかしながら、二重ハローを適用するとフィットが悪いことが明らかになった。 外側ハローの球形 R-3.5 則を SA 107/SA 184 領域で外挿すると そのモデルは大きな予想密度超過となる。これは、外側べき乗ハローのコア半径 を大きくするか、べき乗指数を下げるかすると緩和される。しかし、そうすると 今度は高銀緯で密度勾配が浅くなり過ぎる結果になる。こうして、これまでの ところ、全領域を満足させるモデルは見つかっていない。しかし、将来の方向 がないではない。

　フィットさせる３つの方法　

　特に、等密度線を全部フィットするために、標準ハローを変更する方法が ３つある。

１：べき乗指数を場所により変化させる。　

第１はべき乗則の指数を距離に応じて変更して行く方法である。最近の ヒエラルキー集合モデルによる銀河形成論では、降着ダークマターのハロー密度が 内側では R-1.5 であるが、外側に移ると R-3 から R-4 となる。Dubinski, Carlberg 1991, Navarro et al 1997, Subramian, Cen, Ostricker 2000, Dave et al 2001. 低メタル星のハローは ダークマターハローとは完全に別物である。しかし、星のハローはダークマター ハローのポテンシャルに結局は従うのである。星のハロー遠方の密度分布は ダークマターモデルをテストする方法を与えるかも知れない。

　２： 共焦点楕円体　

　第２の方法はハローの等密度面を共焦点楕円体と看做すことである。すると、 内側は平坦な楕円体、外側は球形の等密度面になる。

　３：c/a = f(R)　

　最後の方法は、Preston et al 1991 の c/a = f(R) 式を使用する。

　その結果　　

　これらの方法は明らかな前進を示すが、収束しない。これはスターカウント のハローパラメターへの反応が鈍いための現象である。フリーパラメターが 増えるとこの鈍さは悪化するのである。

　外側ハローは星流の重なり　　

　一方、二重ハローは定性的には正しいとしても、そのために従来の定量的 解析で取り扱いにくくなっている。外側のハローは滑らかな密度分布を持たず、 星流の重なり合いかも知れない。ハロー密度分布の副構造や折れ目が巨星の 密度分布から直接に観測されている。Majewski et al 2002. それは既に主系列星 Majewski, Munn, Hawley 1994, 1996, Newberg et al 2002, Dinescu et al 2002 や 青い水平枝星 Yanny et al 2000, Ivezic et al 2000, Vivas et al 2001 では言われていた。これらの研究は遠方ではハローが 多く、または完全に星流の重なりから出来ていて、滑らかな分布は内部ハロー にのみ適用されることを示唆していた。

　スターカウントで星流は見えないだろう　　

　ただし、この様な副構造外側ハローが我々のモデルの問題を解決するかは はっきりしない。モデルとの不一致は系統的で、缶一杯のミミズを透かし見る 時のようなランダムなズレではない。さらに加えて、Johnston 1998 によると、 大きな降着事象でさえもスターカウントでは検出できないらしい。もし星流の 空間率が高ければ、高分解でミミズと見えるものがスターカウントではぼやけ てしまうだろう。その上、たった７箇所いかないので系統効果とでたらめ効果を 区別する能力には限界がある。

　二重ハローは有望　　

　もし SA 107/SA184 の過大予想を直すため、フレアする厚い円盤モデルを採用 するなら、ハロー副構造で他の領域、特に SA 141、これは Newberg et al 2002 の外部ハロー星流の方向だが、 の過小予想を説明できるだろう。このように 外側が星流集合からなる二重ハローモデルは興味深い可能性であり、我々の モデルが抱える大きな矛盾の解決となりそうである。

　９．銀河系形成への意味　

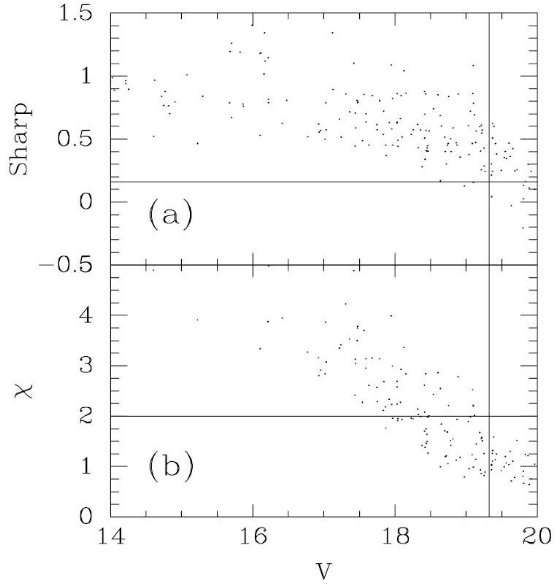
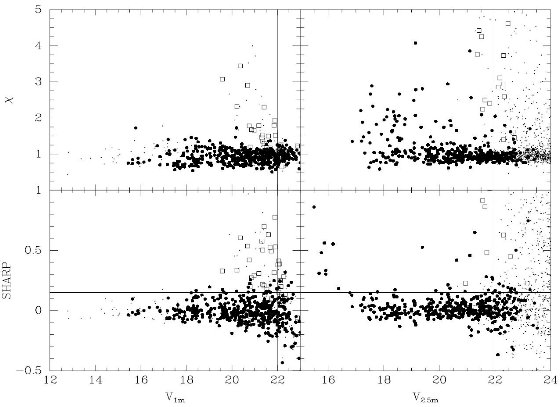
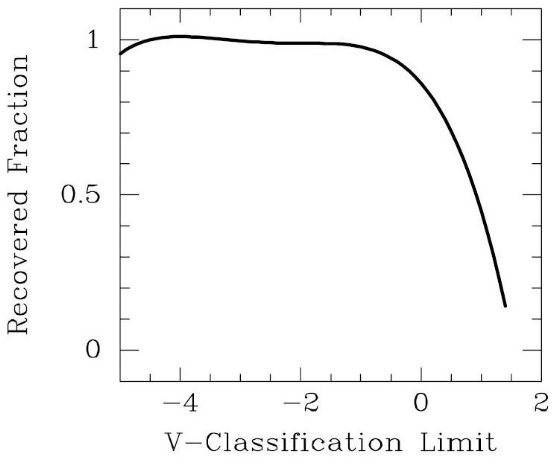
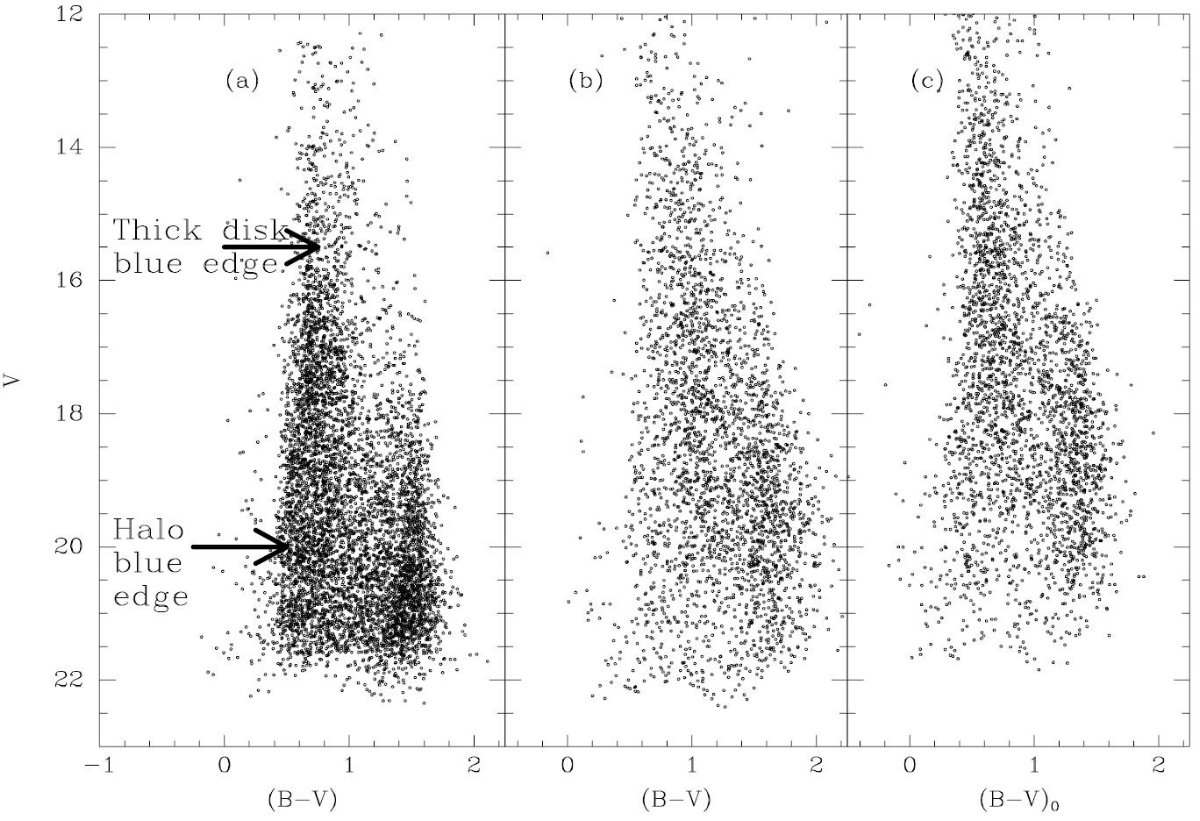
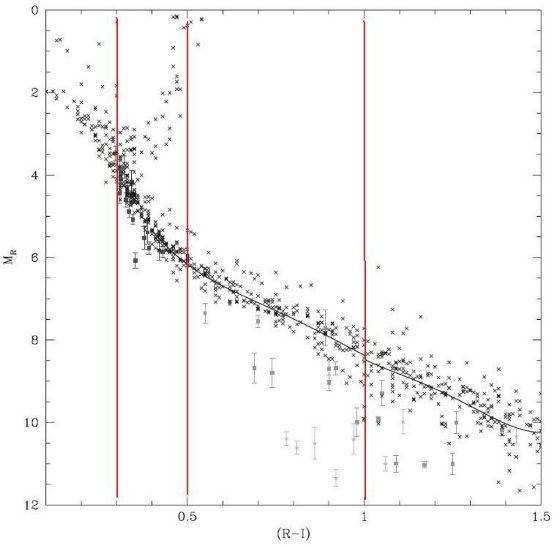
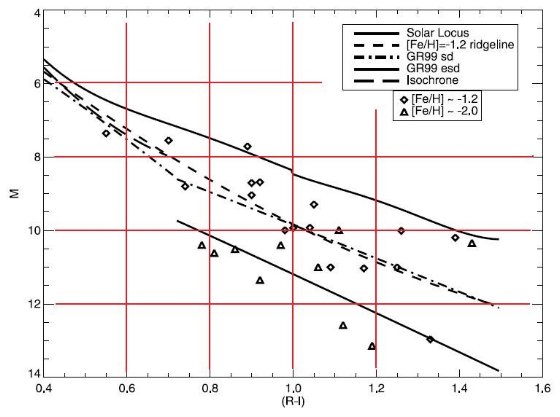
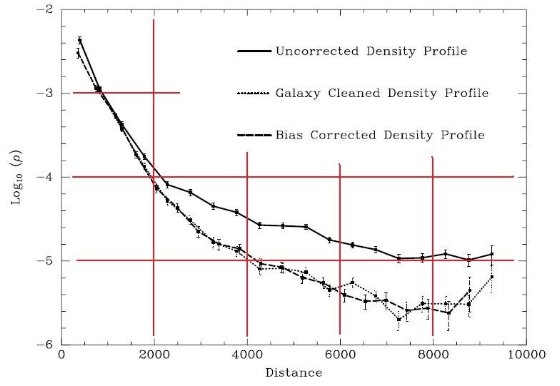
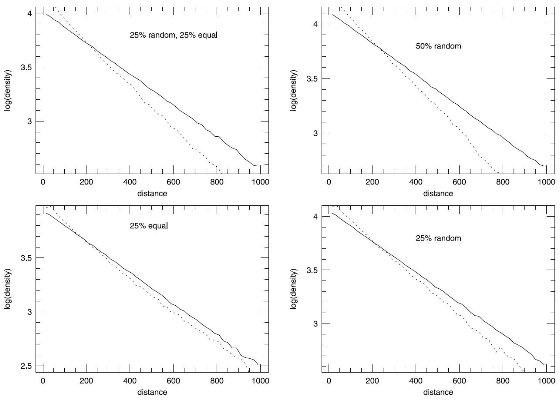
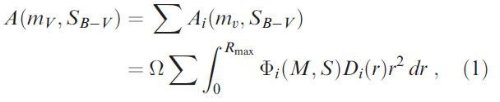潮汐力による運動学的加熱　

　厚い円盤の起源に関し多くのシナリオが提案されてきた。レビューは Majewski 1993 を見よ。その主系列ターンオフカラーから、厚い円盤には数 Gyr より若い 主系列星は殆どないと言える。広く受け入れられている厚い円盤起源は、銀河系 初期にマージャー（Quinn, Hernquist, Fullagar 1993, Walker, Mihos, Hernquist 1996, Huang, Carlberg 1997, Sellwood, Nelson, Tremaine 1998）か、遅れて 落ちてきた星の固まり、Noguchi 1998, によって薄い円盤の潮汐加熱から出来た というものである。潮汐加熱つまりマージャー説では銀河系のガス成分はこの 出来ごとで運動学的に加熱されるが、その後冷えて元に戻り現在の薄い円盤を 形成した。星の方は無衝突系なため未だに力学的に熱いままなのである。

散逸的陥落　

　別の説では、厚い円盤の成因は、急激なハロー形成に始まり薄い円盤の 形成で終わる、散逸的陥没過程の途中で厚い円盤が生まれたとする。Larson 1976, Jones, Wyse 1983. Majewski 1993 は ELS 1962 の最初の説のような 全体的収縮の際に出来た最初の構造であるという考えを支持する観測的証拠を 並べた。そこでは、ハローはその後に小さな恒星集団が降着して来て出来たので ある。Sandage 1990

化学組成と運動特性の証拠　

　加熱説を支持する証拠は化学組成、Nissen, Schuster 1991, Fuhrmann 1998, Gratton et al 2000, Prochaska et al 2000) と運動、Carney et al 1989, Beers, Sommer-Larsen 1995, Ojha et al 1996, が近傍ハローと厚い円盤が 滑らかにつながり、厚い円盤と薄い円盤との間に不連続があることから来ている。 選択バイアスの影響は注意する必要がある。厚い円盤星は化学組成に基づいて その運動を調べる候補に選ばれたり、逆に運動学的特性から化学組成を調べる 候補に選ばれたりすることが多い。後から加熱が起きたシナリオでは、最も 極端な運動学特性を持つ星と、最も極端な化学組成を持つ星は同一である。 より完全度の高い球状星団 Majewski 1992, 1995, Chen 1997, 1999, Chiba, Beers 2000 によると、両円盤に運動学的な勾配が存在し、厚い円盤と球状星団 の間には断絶が存在する。

厚い円盤の年齢と薄い円盤の年齢　

その上、そのように激しい加熱は厚い円盤の年齢と 薄い円盤の年齢の間に制限され得る。したがって、それが起きたのは銀河系の 歴史のかなり初期である。というのは薄い円盤の最も古い星の年齢は 8 Gyr と 12 Gyr の間であるから。Janes, Phelps 1994, Bergeron, Ruiz, Leggett 1997, Leggett, Ruis, Bergeron 1998, Jimines, Flynn, Kotoneva 1998, Wood, Oswalt 1998, Knox, Hawkins, Hambly 1999, Carraro, Giardi, Chiosi 1999, Montgomery et al 1999, Liu, Chaboyer 2000. 厚い円盤は通常薄い円盤より 高齢と考えられている。 Gilmore, Wyse 1987, Carney et al 1989, Rose, Agostinho 1991, Gilmore et al 1995. 気を付けなければいけない重要な点は 年齢の差、通常 1- 2 Gyr は不定性より小さいことである。フィールド星の 年齢を決める困難さを考えると、薄い円盤と厚い円盤の年齢差は未だ決着が ついていない問題である。

星形成史からの証拠　

　我々の見解では、マージャー説に有利な最近の研究結果は組成パターンから 導かれる星形成史は散逸形成からの期待とは合わないことである。Prochaska et al 2000. ただし、彼らの厚い円盤星は比較されている薄い円盤星と 大きな組成の重なり合いがないので、この証拠は注意する必要がある。さらに、 横向き銀河で厚い円盤が見えない, van der Kruit, Searle 1981, Morrison, Boroson, Harding 1994, Morrison et al 1997, Fry et al 1999 のでもっとストカスティックな過程が働いているのかも知れない。 		ハローの起源　

　ハローの起源は原始雲の急激な崩落による (ELS) か原始銀河片の 降着（Searle, Zinn 1978）に依るかである。降着説は冷たいダークマター 宇宙論と合う。それはヒエラルキー的な銀河形成（White, Rees 1978, Navarro et al 1997）を予想するからである。第８章は双方の説の証拠を述べている。

銀河系の四成分　

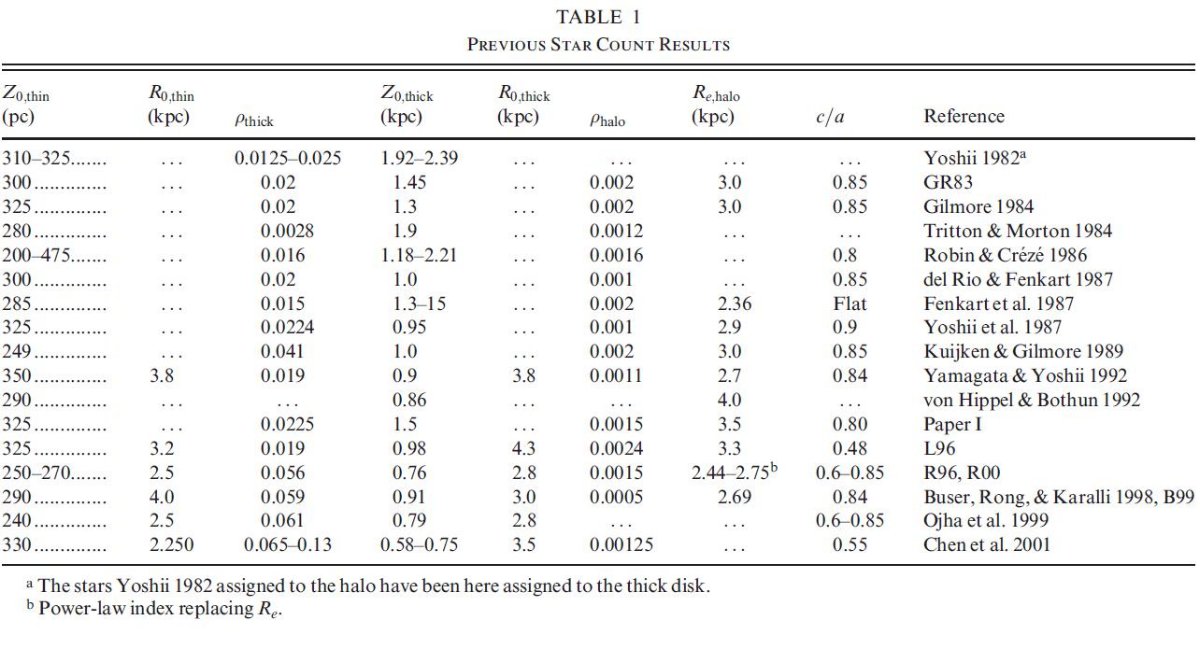
　銀河系の四成分、古い円盤、厚い円盤、内側ハロー、外側ハロー、は文献 に現れた銀河系の特徴の殆どを説明する。

外側ハロー　

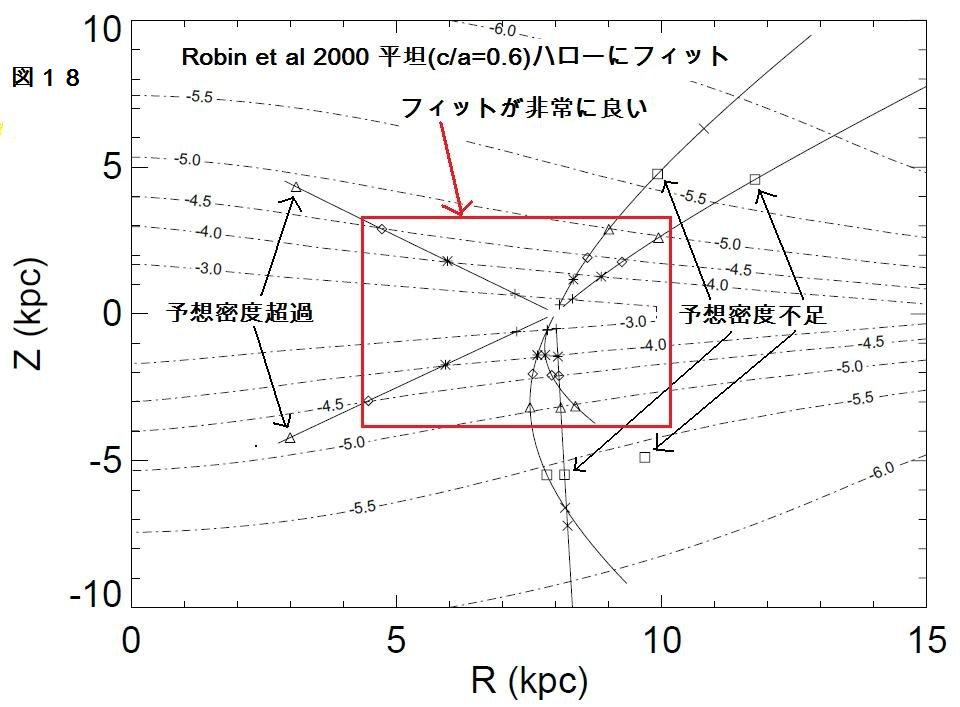
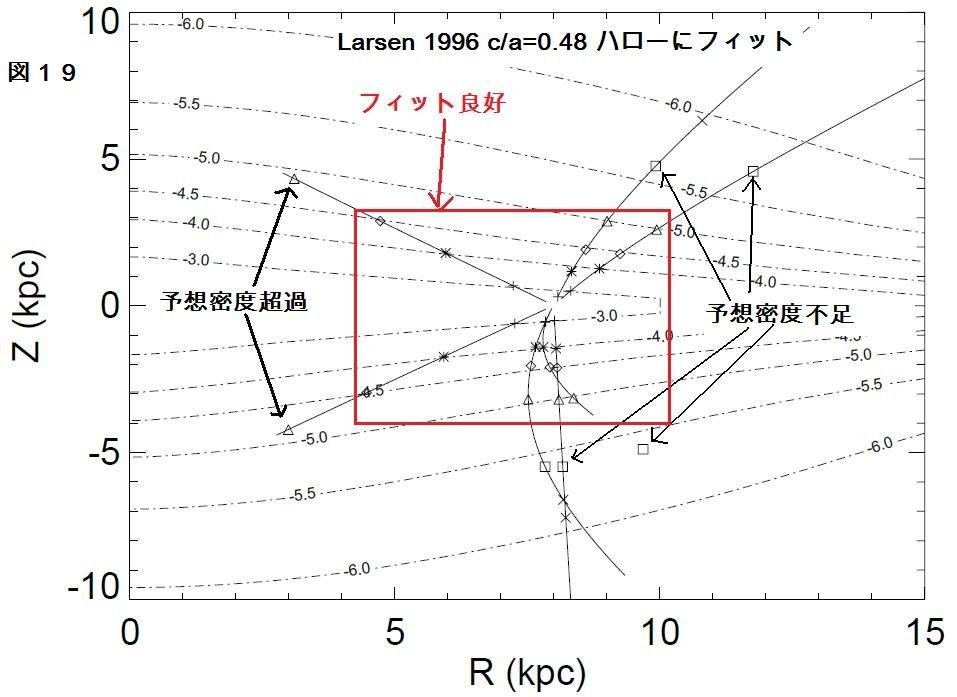
　外側ハロー、Zinn 1993, Chiba, Beers 2000, は Majewski 1993 では 単にハローと呼ばれる。この成分は比較的近傍の主系列星を扱った、 Robin et al 1996, Larsen 1996, Robin et al 2000 では完全に 抜けている。形は球状に近く、位相空間内での副構造を示し、化学的に 不均一である。これは球状星団や矮小銀河の降着から生まれた。内側 ハローとはつながっていない。

内側ハロー　

　内側ハローは Zinn 1993, Chiba, Beers 2000 が述べているように銀極では 厚い円盤と区別しにくい。そのため厚い円盤と混ざり合って Majewski 1992, 1993, 1995, や論文 I で言う IPII または、Robin et al 1996, Larsen 1996, Robin et al 2000, Chen et al 2001 が言う「ハロー」となる。この内側ハローは平坦で 運動特性とメタル量の勾配を有している。そして厚い円盤と化学組成、運動特性 の点で重なり合う。内側ハローは ELS 的な崩落の産物であるらしい。Sandage 1990.

厚い円盤　

　すると厚い円盤は、Robin et al 1996, Chew et al 2001, Prochaska et al が 述べているように、稠密で化学的にも運動学的にも均一な構造である。これは おそらく銀河系の歴史の早期のマージャーで形成されたものであろう。

ハローのハイブリッドモデル　

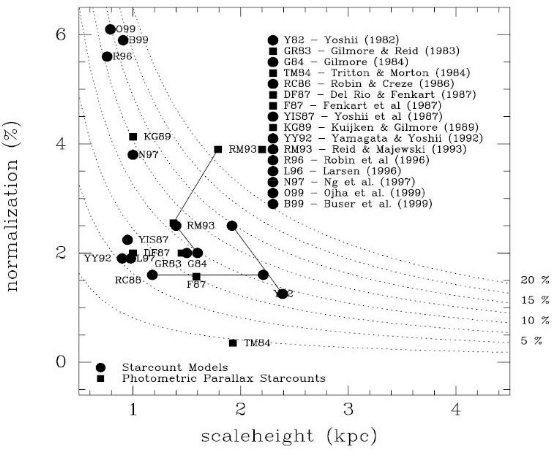
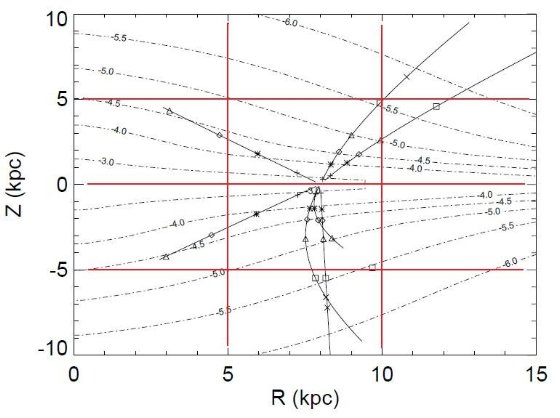
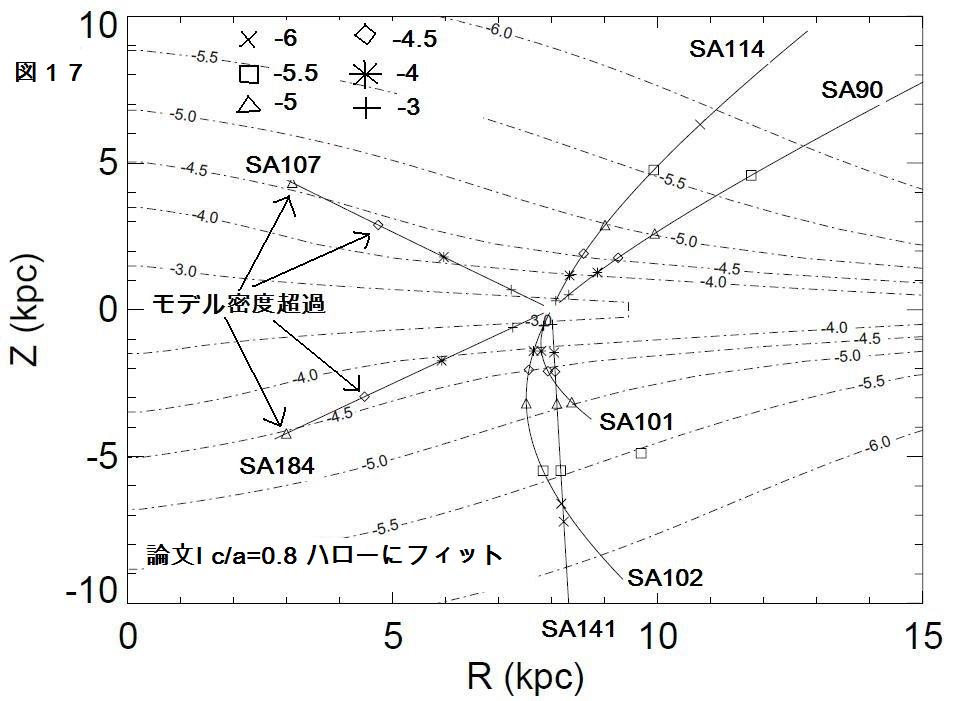
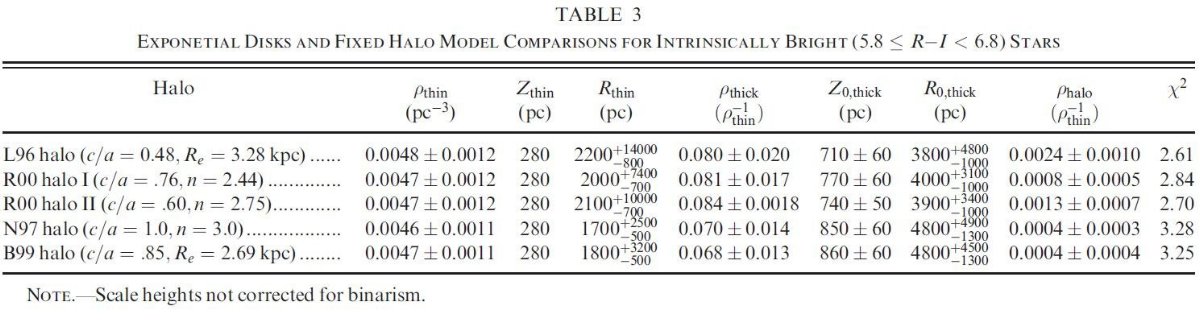
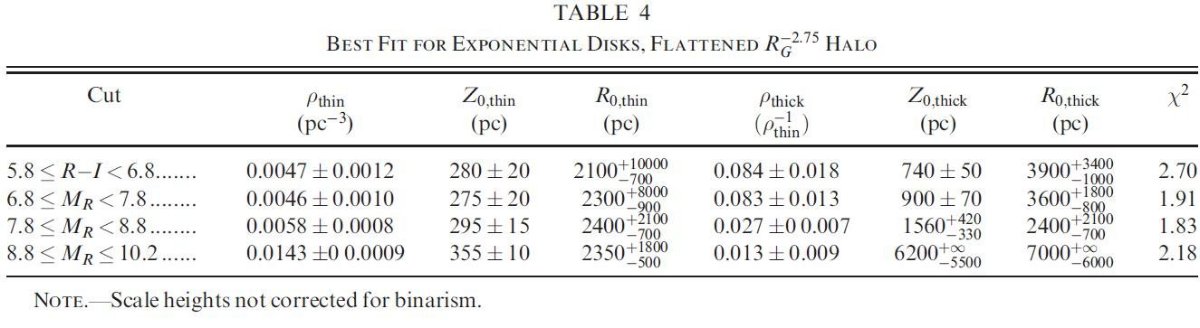
　この様なハローのハイブリッド形成モデルは Sandage 1990, Majewski 1993, Norris 1994, Chiba, Beers 2000 が提案したものである。スターカウントがこの モデルに貢献できるのは、進化したモデル化とカラー分布、紫外超過の詳細な 研究によって、ハロー種族の形と星種族の組成と年齢を明らかにすることである。 それらは今後の我々の研究で追究するテーマである。単純な標準モデルでは 我々の測光視差による密度分布を説明できなかったことはハイブリッド形成 モデルを支持するものと言える。例えば、内側銀河系の予想値超過は厚い円盤 のフレアリングで説明できるだろう。さらに、外側銀河系の過小予想値は第二の 球形ハローの導入で説明可能である。

銀河系のモデル　

　本研究から浮かび上がってきた銀河系の姿は、大規模崩落と降着の両方 が現在の星種族を形作るのに大きな役割を果たしたということである。降着過程 は降着天体が外側ハローに含まれて行くことと、特に大きな天体の降着により 初期の薄い円盤を潮汐作用で膨らませた点でその存在を現わしている。大規模 崩落は内側ハローの形成を担ったのであろう。

　１０．結論　

　カプタイン選択領域七箇所での測光視差サーベイは多くの興味ある結果を産み 出した。それらは、

１．薄い円盤のスケール高　

薄い円盤はスケール長 2 - 2.5 kpc, スケール高 230 pc の二重指数関数で良く表現される。この軸比は横向き Sc 銀河で見られる 値と一致する。観測される最も暗いグループの星はスケール高が上昇 350 pc の 証拠が見られた。興味深いことに最近の結果によれば、白色矮星の薄い円盤スケ ール高もまた薄い円盤の標準スケール高よりずっと大きい。Majewski, Siegel 2002, Nelson et al 2002. しかし、もし暗い星では連星率が低下するならやはり 同様の結果が得られることを注意しておく。　

２．厚い円盤は　

　厚い円盤はスケール長 3 - 4 kpc, スケール高 700 - 1000 pc の二重指数関数 で良く表現される。近傍の古い星の内 6 - 10 % が厚い円盤に属する。円盤が フレアしているらしい証拠がある。それは厚い円盤の起源が運動学的加熱である という説と合致する。 		３．連星　

　種族 II の連星率が 50 % なら、薄い円盤と厚い円盤のスケール高は青い星 に対して 350 pc, 900 - 1200 pc となる。薄い円盤暗い星のスケール高は 440 pc になる。

４．ハロー　

　ハローの密度則は収束しなかった。一般には平坦, c/a ≈ 0.6, でべき乗 則 ρ ∝ R-2.5 は割りと良いが。

５．二重ハロー　

　我々のモデルと観測との差を縮めるためには、内側が平坦で外側が丸い二重 ハローの採用がよさそうである。外側は実際には重なり合う星流の集合である。

６．フレアリング　

　厚い円盤のフレアリングと二重ハローからは、銀河系が少なくとも部分的には 系外天体の降着により成長してきたことを示す。