|
可視・電波分光から元素量を導出 可視・電波分光を合わせて、広い銀河中心距離 RG に渡る HIIR の 元素組成を測った。電波再結合線を用い、 3.5 kpc < RG < 13.7 kpc の 67 HIIR に対して正確な電子温度を定めた。この温度は用い、次に 33 HIIR の可視スペクトルから O, N, S, Ne, Ar, He+ の存在量 を定めた。 電子温度 電子温度の精度は 5 % である。電子温度と ([OIII]+[OII])/Hβ との間には 強い相関がある。異常に狭い再結合線が何本か検出され、そのライン巾のみから 出した電子温度の上限は 4000 - 5000 K である。これは低温度 HIIR の存在を明らか にした。 |
温度勾配 温度勾配 (433±40) K/kpc が見出された。これは温度勾配が メタル量効果であるという仮説と合致する。しかし、同じ銀河中心距離でも 電子温度に 2000 K のばらつきがある。これは電子密度が HIIR 毎に異なる ためと、励起星の有効温度の違いによるのであろう。 元素組成勾配 酸素の組成勾配は -0.07±0.015 dex/kpc である。窒素の方はそれより うんと急ではなく、-0.09±0.015 dex/kpc で、硫黄は それよりずっと平坦な -0.01±0.015 dex/kpc であった。ネオンも同様に 平坦らしいが、アルゴンは酸素と似た勾配を持つ。銀河中心距離の等しいところでの 組成のばらつきは小さく 20 % 以下である。He+/H+ 比 の勾配は認められなかった。 |
|
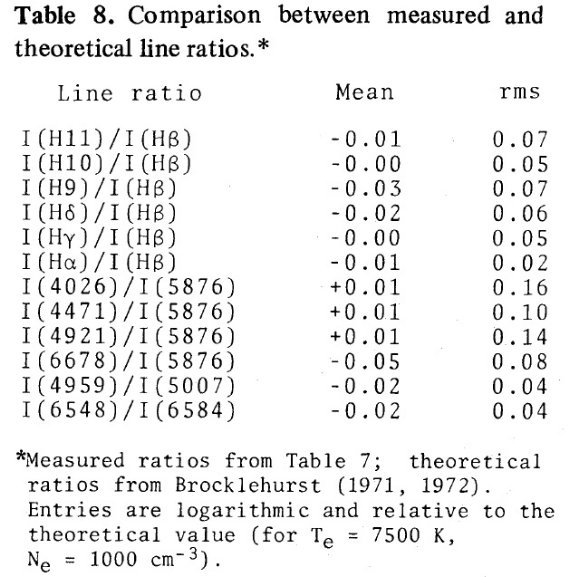
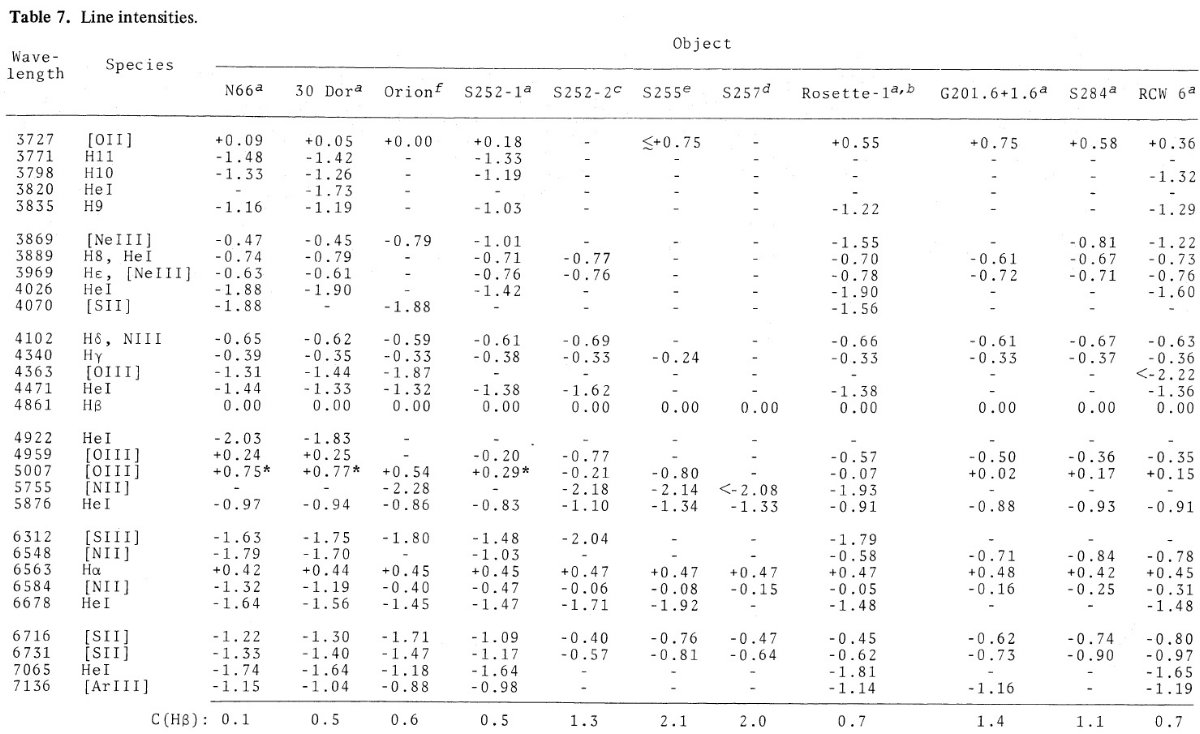
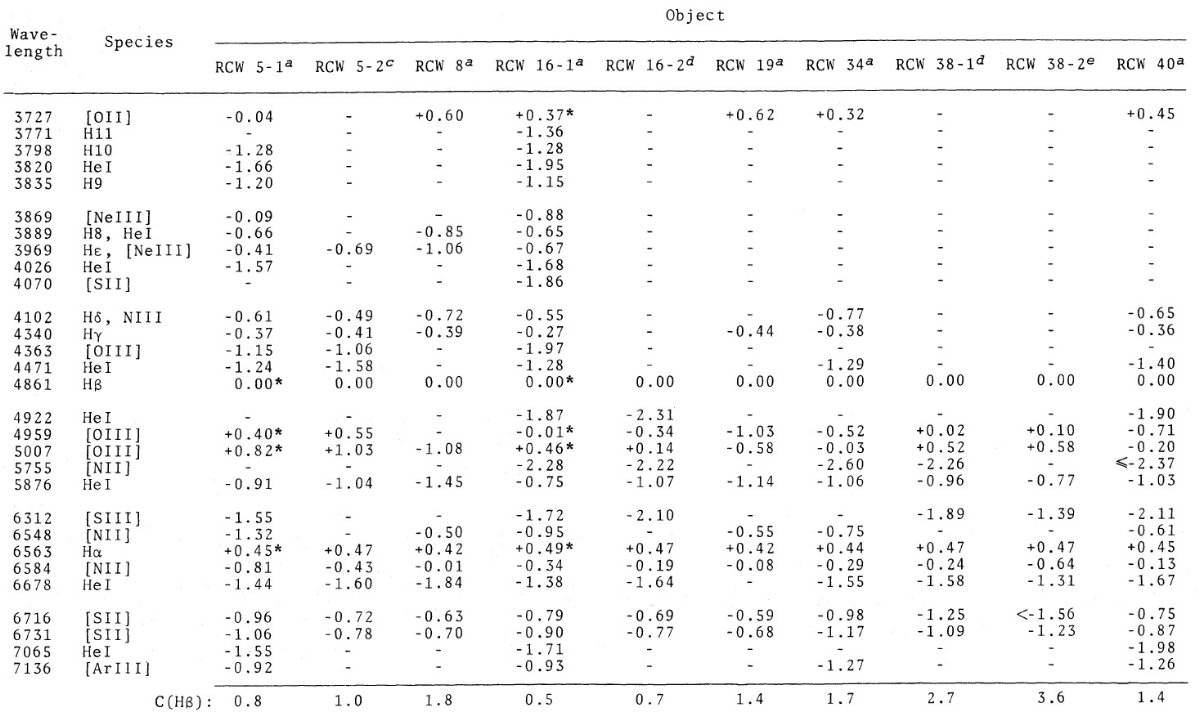
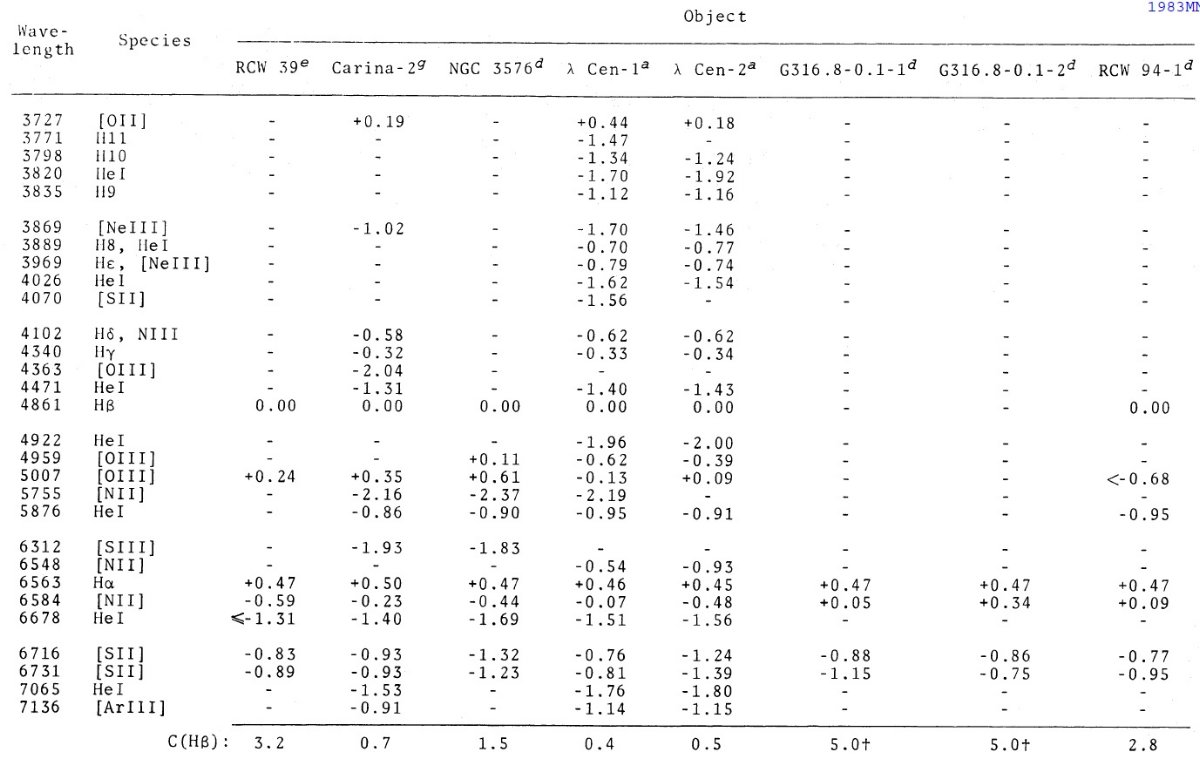
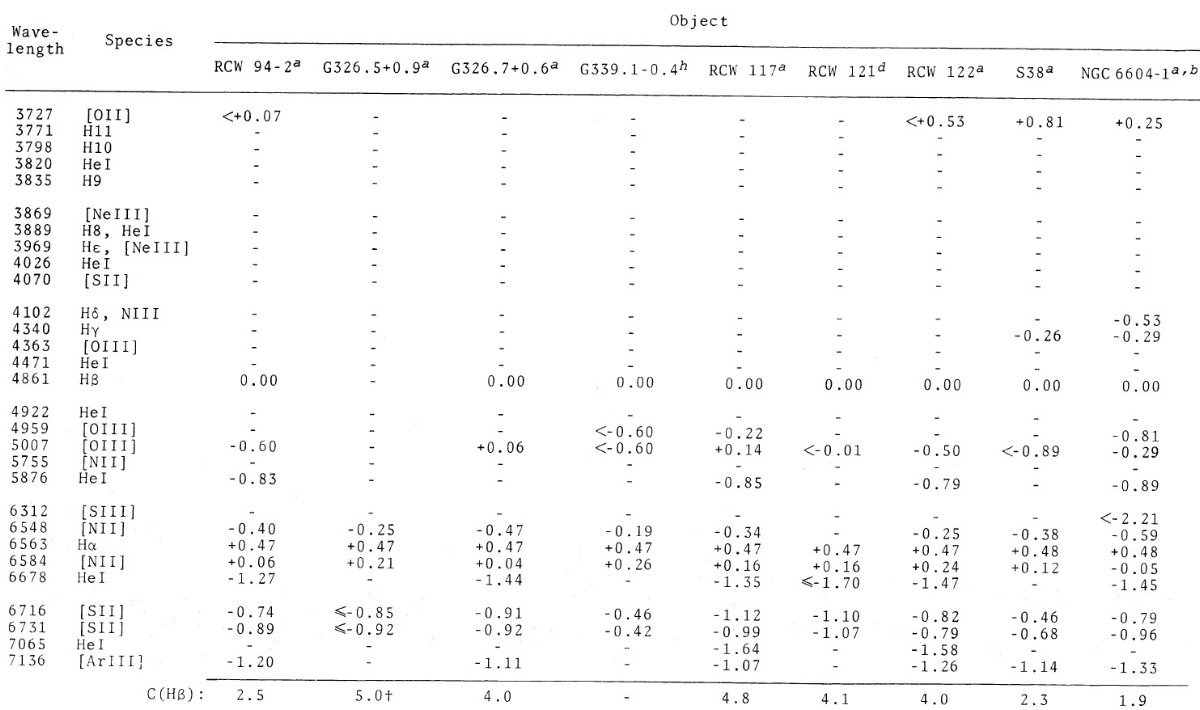
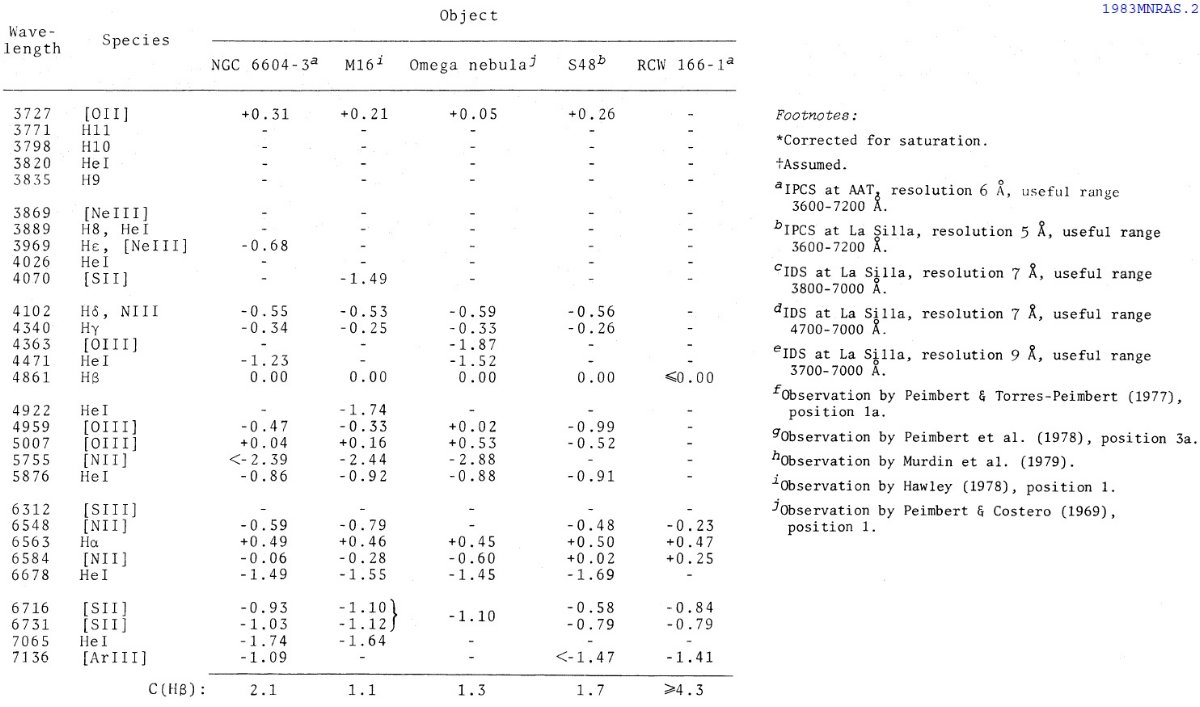
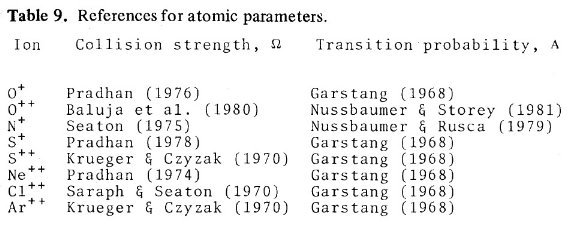
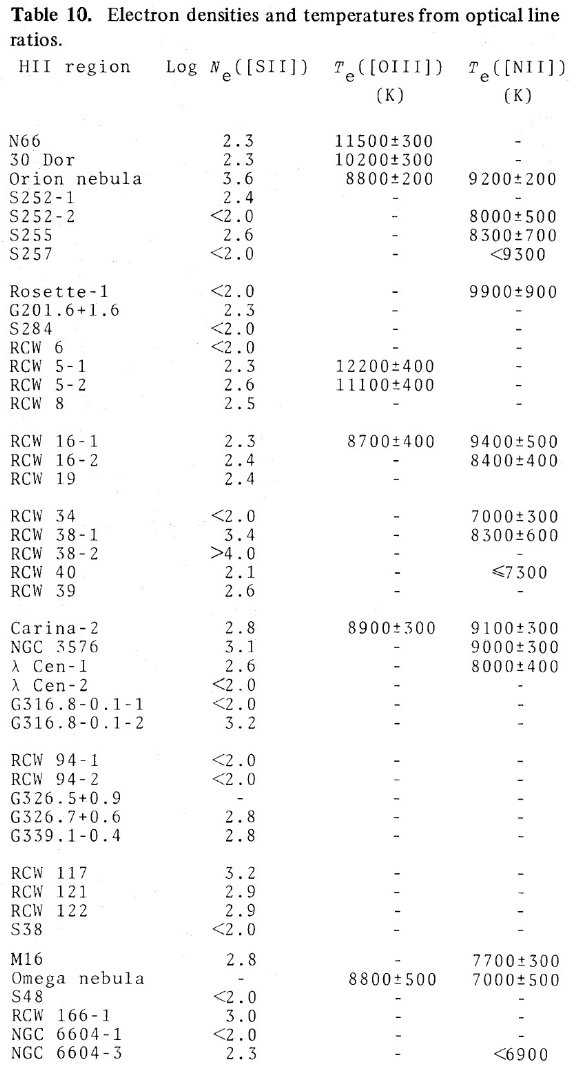
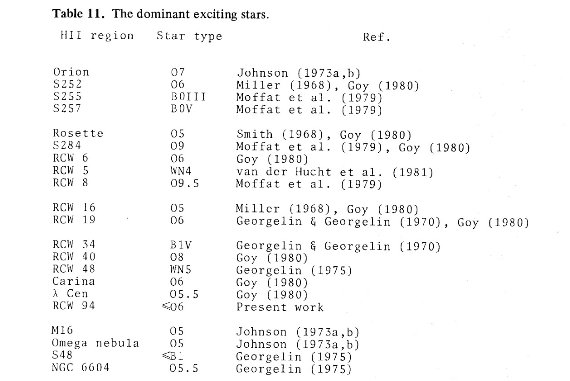
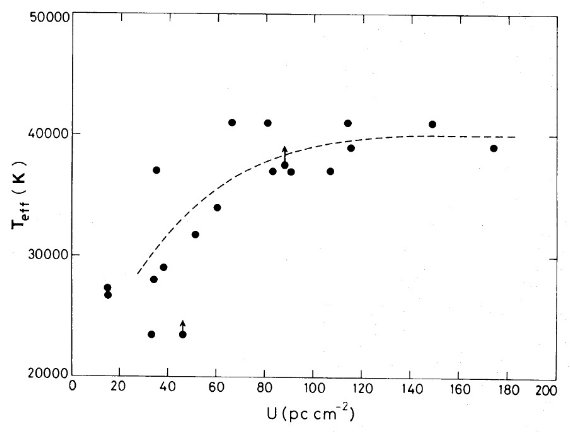
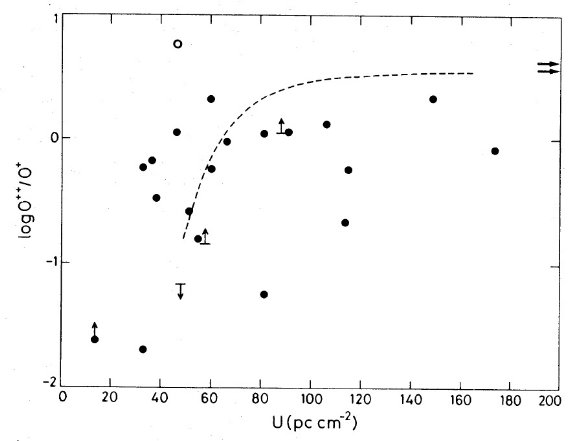
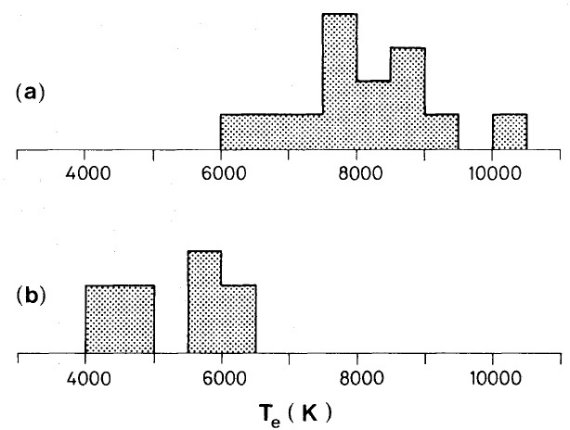
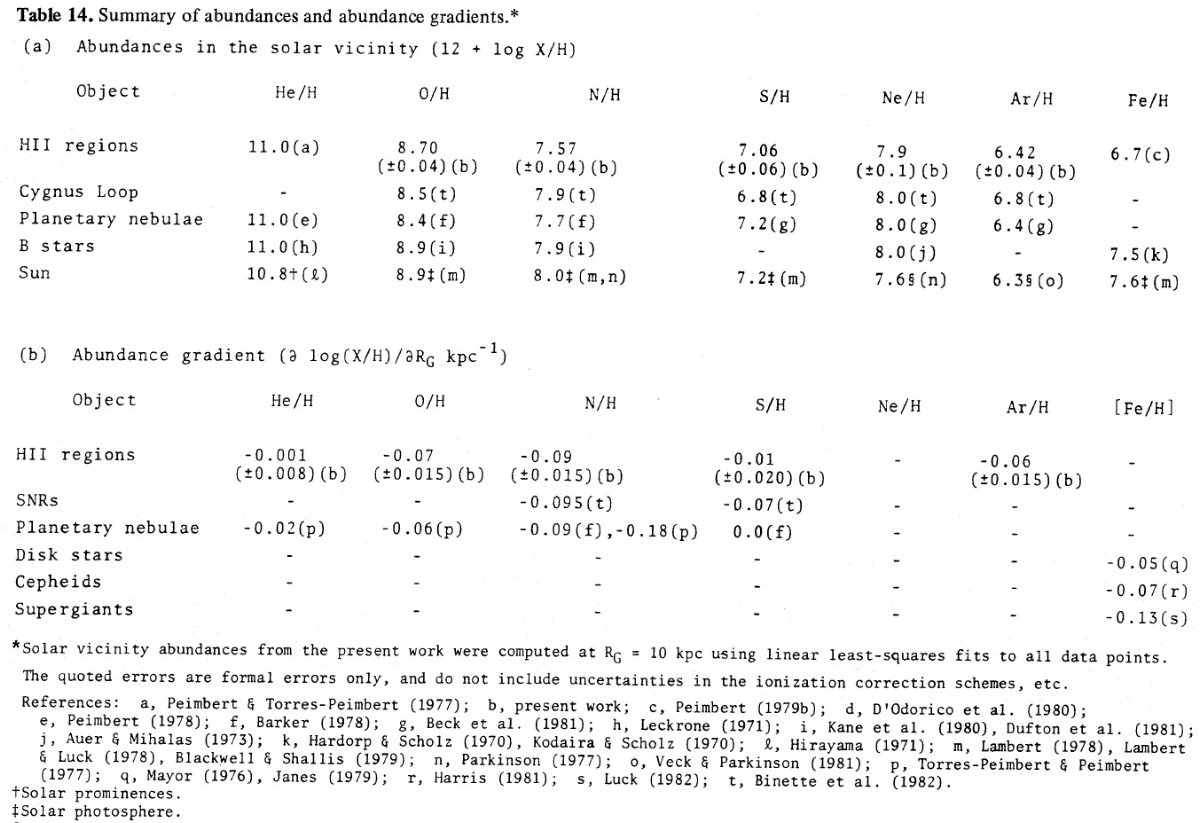
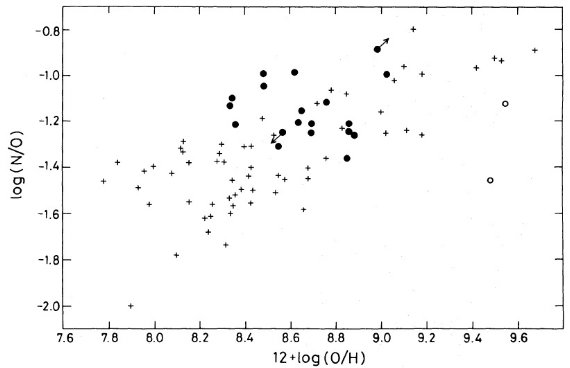
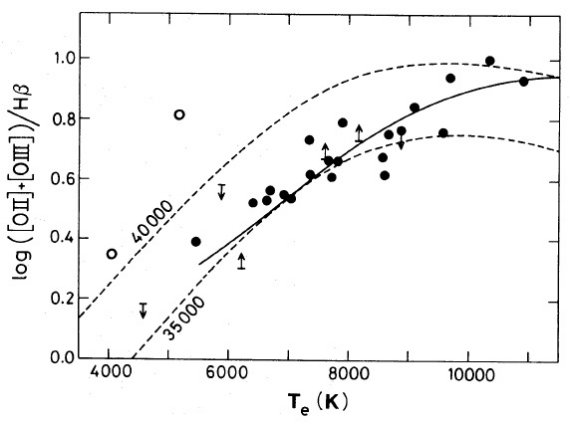
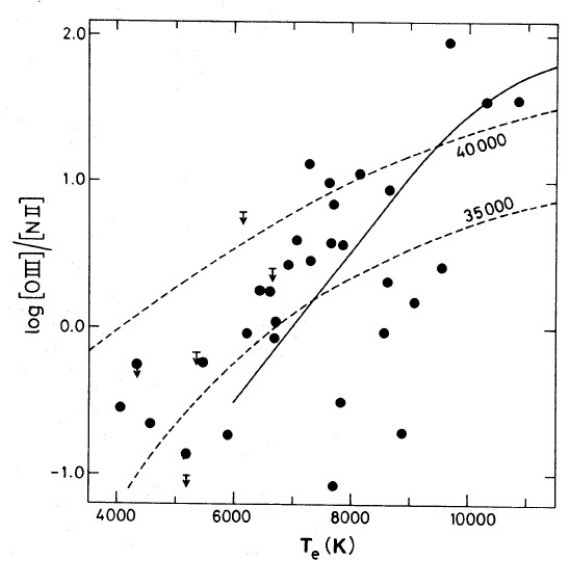
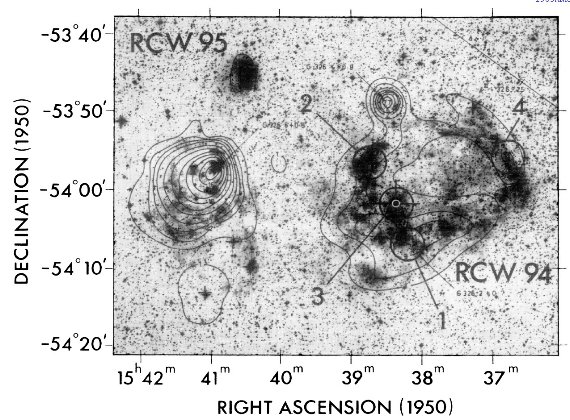
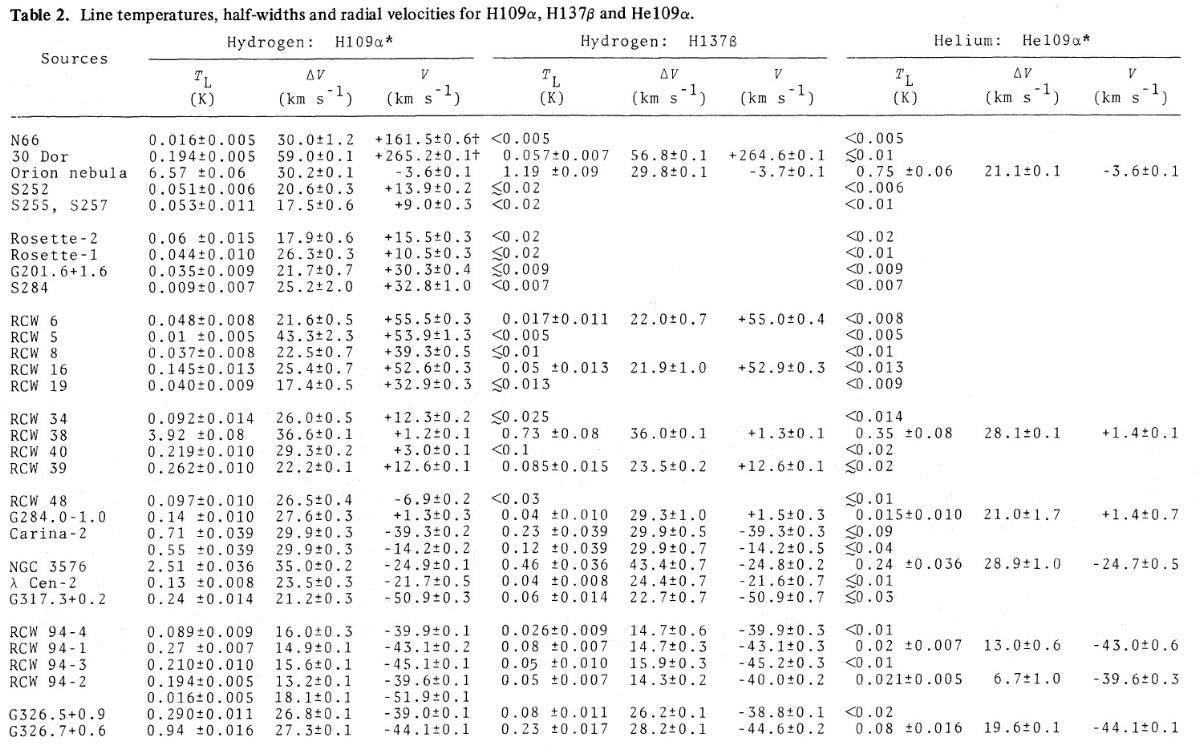
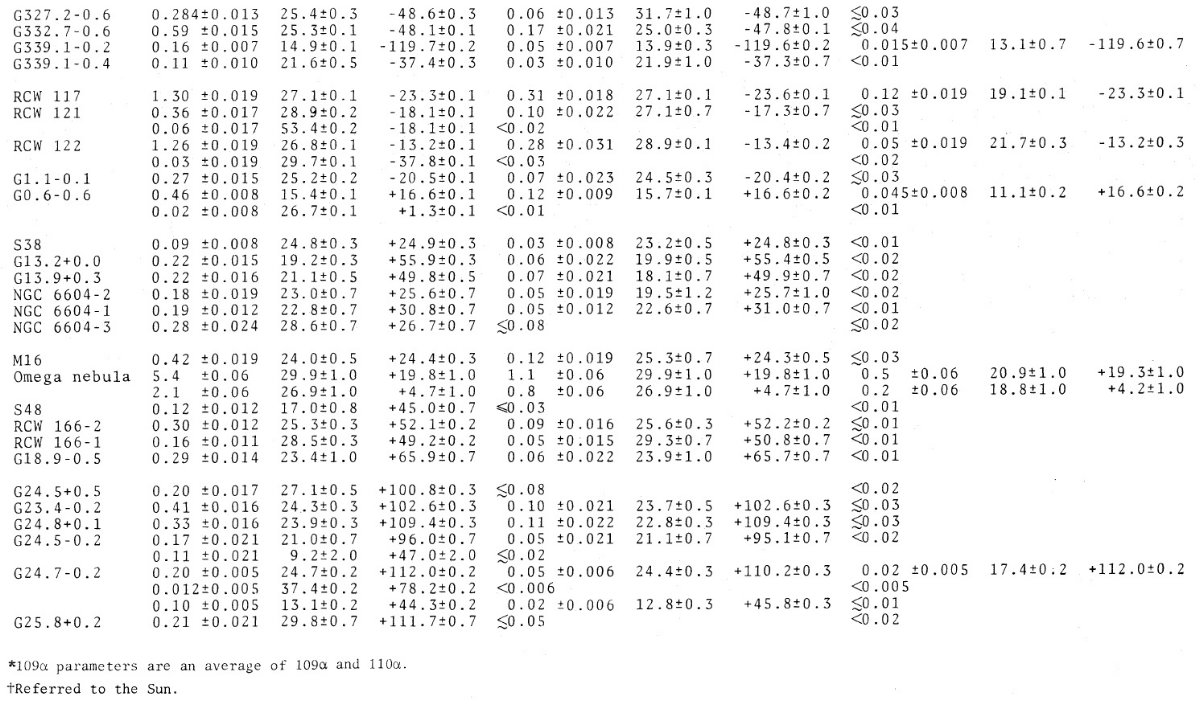
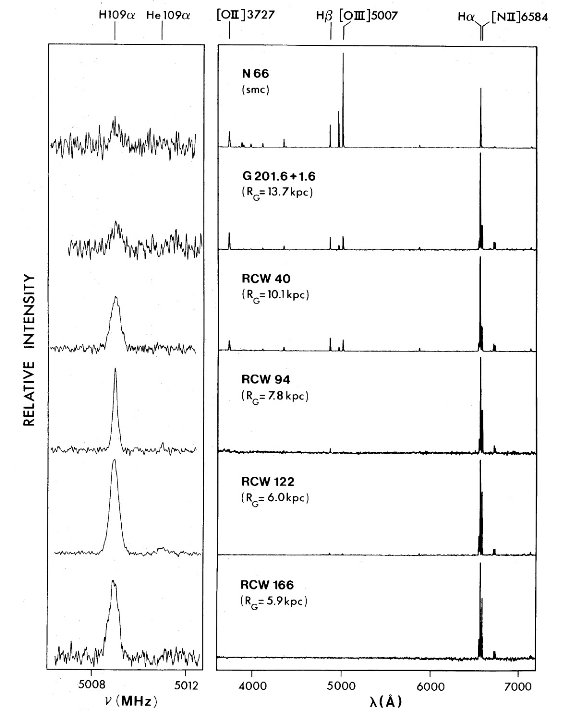
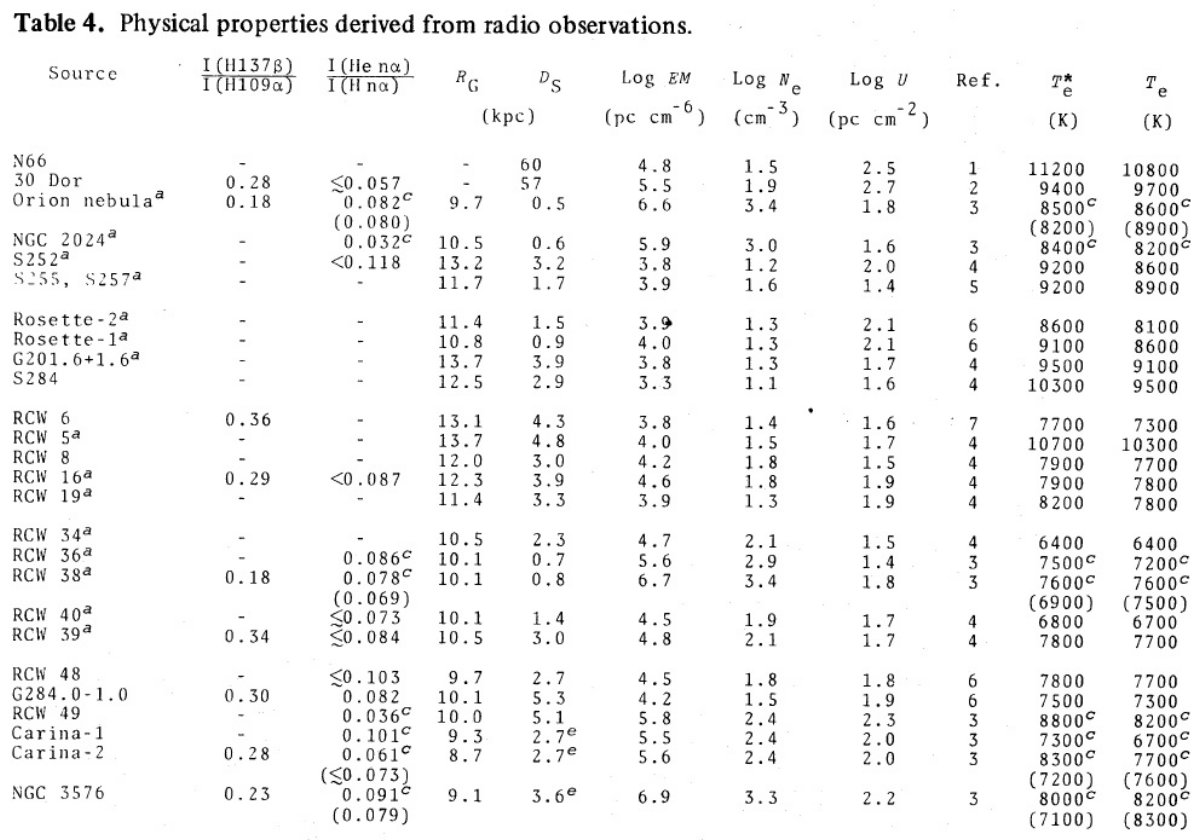
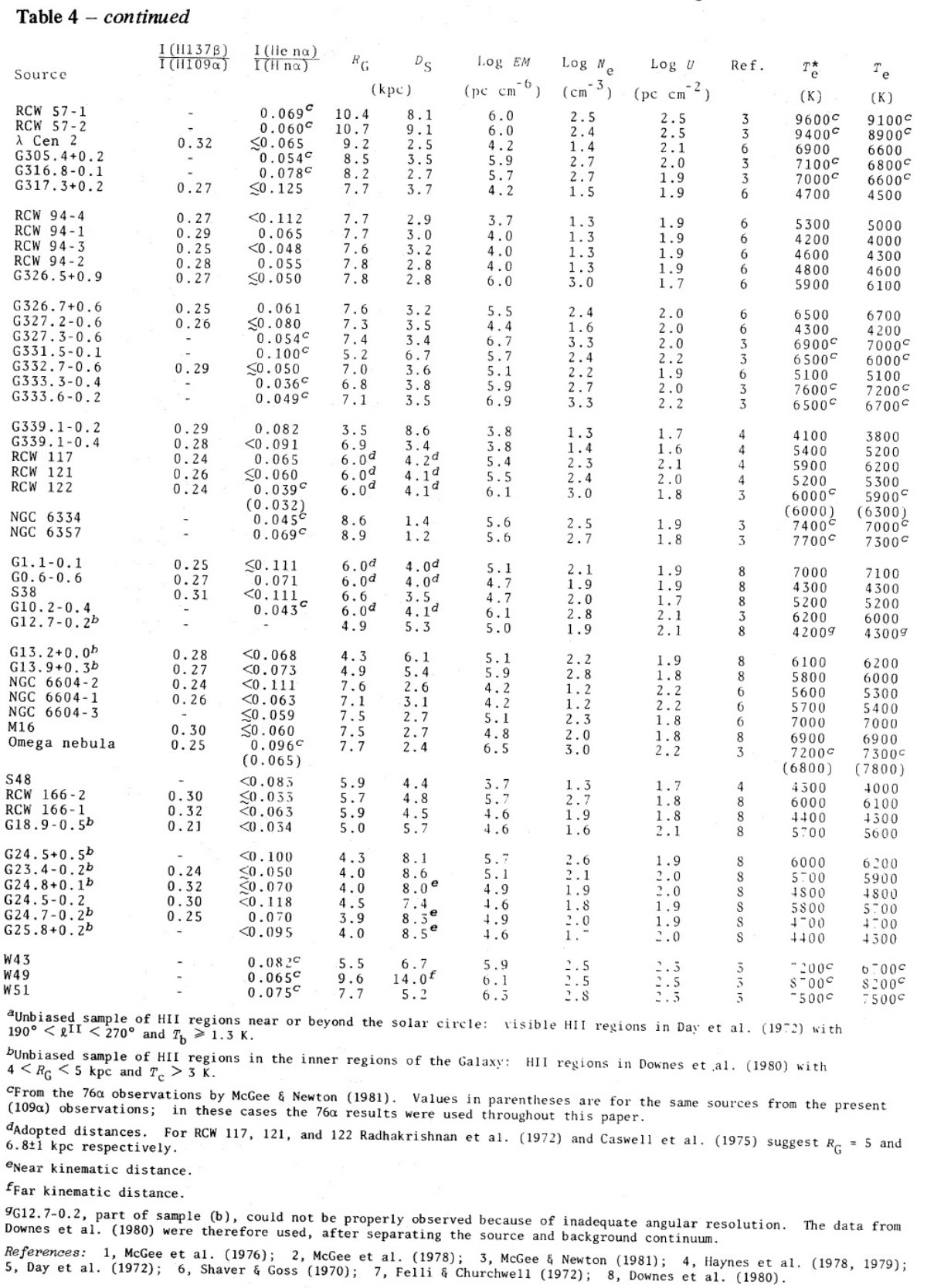
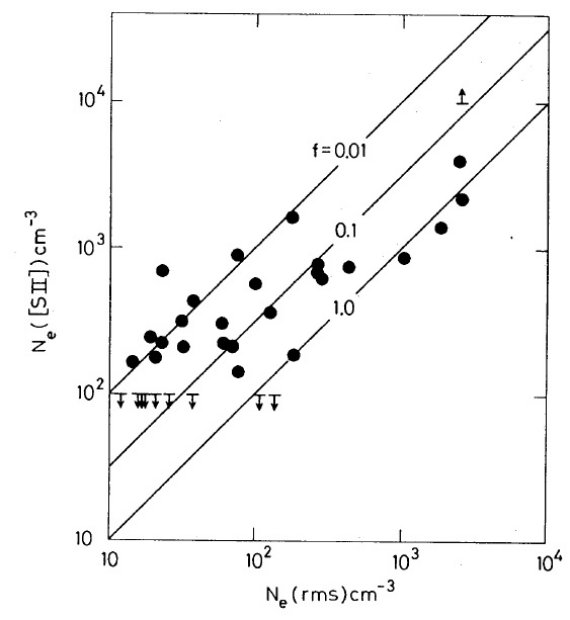
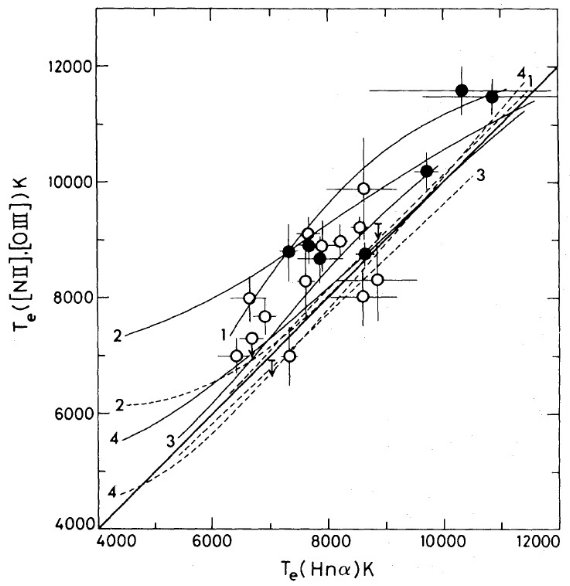
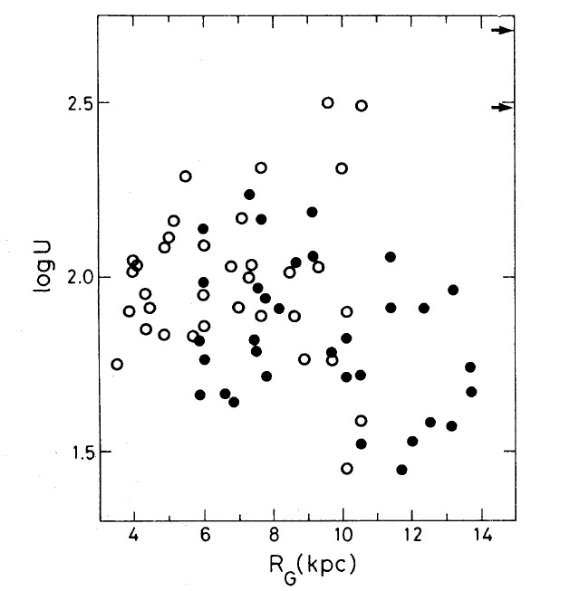
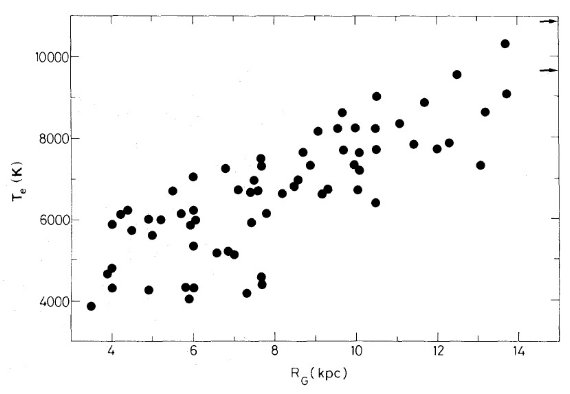
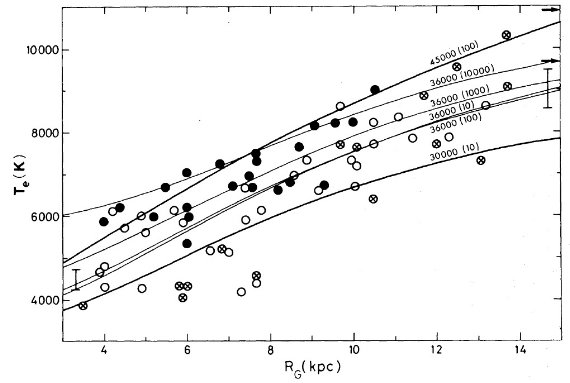
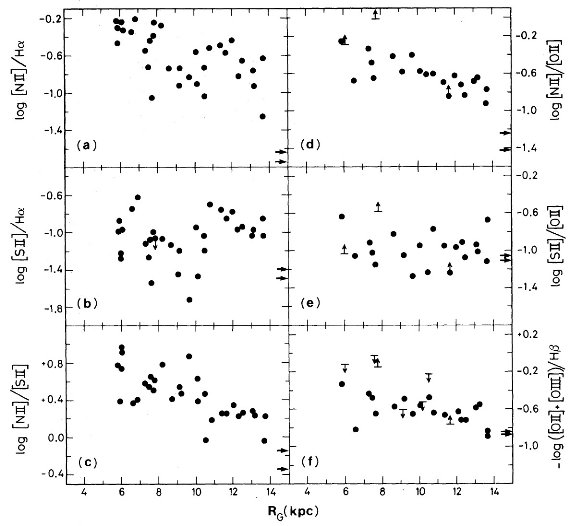
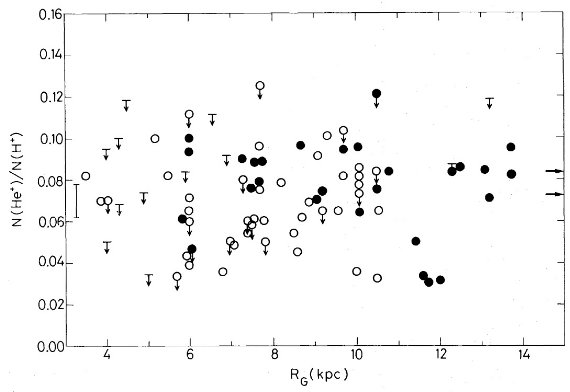
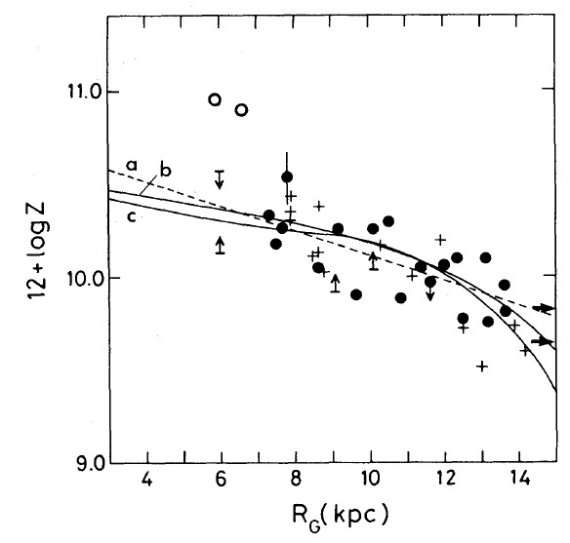
電子温度 電子温度は通常 [OIII]4363 か [NII]5755 強度から決める。どちらも非常 に弱いラインでかなり熱く(≥ 7000 K), かつ明るい HIIR でないと検知さ れない。このため、組成が決められる HIIR の数は限られる。 これを迂回するいくつかの方法が考えられている。 電波 我々の銀河系内 HIIR では幸いなことに電波観測が併用可能である。再結合線 を使うと電子温度は数 % 精度で決まる。 電子温度勾配 電波観測から電子温度には銀河中心距離による勾配が検出されている。しかし、結果は 確実でない。そこで、新しい電波、可視分光観測を多数の HIIR に行った。 R = 3.5 - 13.7 kpc の 67 HIIR に電波観測、R = 5.9 - 13.7 kpc 33 HIIR に可視 分光観測を行った。 |
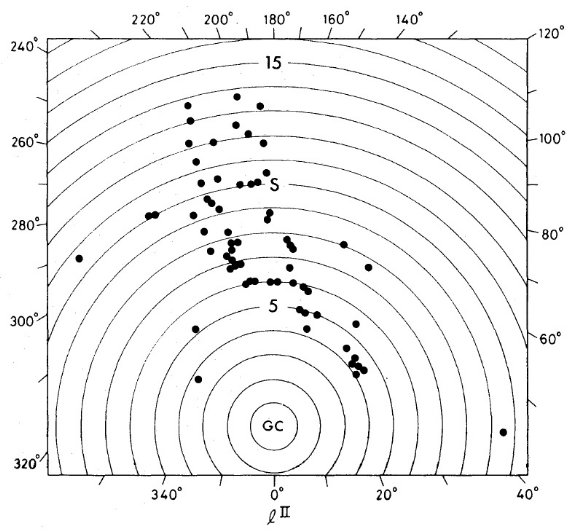
 図１．HIIR の分布(Ro = 10 kpc)。 |
２．１．観測と結果観測結果の表示観測はパークス 64-m 望遠鏡で 1979 - 1980 に行われた。観測結果は 表１、２に示す。表１は天体位置と連続波温度を、表２は天体名、と 主な３本、 H109α, H137β, He109α について、 ライン温度、巾、速度を示す。図２には観測例を示す。幾つかのライン巾 が異常に狭いことに注意せよ。これは後に論じる。電波観測から導いた 物理量を表４に示す。表４の第４，５列には Schmidt 1965 の回転曲線を用いて 得た運動距離を示す。 ２．２．電子温度 図２．スペクトルの例  図３．Te*/Te 値。丸は 109α と 76α 観測を示す。Te* = 予備的に得たTe, Te = 解析した Te (らしい) |
 表１．天体位置と連続波温度  表３．多分 C109α と S109α ライン |
３．１．可視観測可視分光観測は 3.6 m ラシーヤと AAT で行われた。天体位置を表６に、 ライン強度を表７に示す。 表８．ライン強度比の観測とモデル値との比較。 |
 表６．可視観測 |
３．２．電子密度 表９．原子パラメタ―  図７．HIIR の電波と可視のスペクトル例。 |
 表１０．可視スペクトルから導いた電子密度と温度 |
４．１．物理パラメタ―元素組成の導出には、電子密度、電子温度、励起星の有効温度が必要である。４．１．１．電子密度図９は局所 [SII] と rms 電子密度の比較である。局所密度は rms 値より大きい。 これは良く知られている現象でフィリングファクター f = 0.1 である。 図９．局所 [SII] と rms 電子密度の比較。 |
４．１．２．電子温度 図１０．電波再結合線から導いた電子温度と可視 白丸＝[NII], 黒丸＝[OIII] ラインから導いた電子温度の比較。曲線はモデル。 |
４．１．３．励起星の有効温度表１１に我々の調べた 21 HIIR のうち 11 個の励起星を載せた。図１２を 見ると、有効温度と励起パラメタ―の相関は良い。なので、電波再結合線 観測から決まる励起パラメタ―から有効温度を推定できる。図１４を見ると、 励起パラメタ―に勾配が見つかる。分散は大きい。相関係数＝０．２６で、 Rc ≥ 8 kpc で 中間値 70 pc cm-2, Rc < 8 kpc で 中間値 93 pc cm-2 である。  表１１．主な励起星  図１２．励起パラメタ―と有効温度の関係。プロット点＝表１１からの HIIR. |
 図１３．励起パラメタ―とO++/O+比の関係。 白丸＝ RCW5, 水平矢印＝ マゼラン雲の N66 と 30 Dor. 破線＝ Stasinska 1980 モデル。  図１４．銀河中心距離による励起パラメタ―の変化。 黒丸＝ 可視観測を行った HIIR, 水平矢印＝ マゼラン雲の N66 と 30 Dor. |
４．２．１．ヘリウム４．２．２．他元素 |
５．１．温度勾配 図１５．(a) R ≥ 10 kpc と (b) 4 kpc < R < 5 kpc の２サンプルの 電子温度分布。 第２章で述べたが、 R が小さいのと大きい HIIR の選択に努力した。図１５に 二つの R グループでの電子温度分布を示す。全サンプルの温度分布を図１６に 示す。電子温度変化は次式で表される。 Te(K) = (3159±110) + (433±40)R(kpc) R < 8 - 10 kpx で勾配が平坦になる(Chiosi, Matteucci 1982) とか、 R < 5 - 6 kpc で Te が急落する (Mezger et al 1979) という証拠はなかった。 |
 図１６．電子温度と銀河中心距離の関係。  図１７．電子温度と銀河中心距離の関係。 黒丸：U > 80 pc cm-2 かつ Ne > 100 cm-3. 十字丸：U < 80 pc cm-2 かつ Ne < 100 cm-3. 曲線は組成勾配式を仮定して求めたモデル温度。 |
５．２．ライン強度比の勾配図１８には幾つかの組み合わせのライン比の銀河中心距離変化を示した。 右側の矢印はマゼラン雲。使用ラインは [NII] 6584, [SII] 6716+6731, [OII] 3727, [OIII] 5007 である。幾分かの勾配が存在することは明らかである。 [NII]/Hα と [SII]/Hα は電離度の変化に直接影響されるが、 他の比はそれほどでない。それで、図１８(a), (b) の点のばらつきが最も大きい。 影響の最も少ないのは ([OII]+[OIII])/Hβ で図１８(f) はもっともきつい 相関を示している。 |
 図１８．幾つかの組み合わせのライン比の銀河中心距離変化。右側の矢印は マゼラン雲。使用ラインは [NII] 6584, [SII] 6716+6731, [OII] 3727, [OIII] 5007 |
|
N(He+)/N(H+) の R 変化を図１９に示す。明白な勾配 は認められない。 He+/H+ = (0.074±0.003) - (0.000±0.001)R(kpc) 分散は観測誤差(10 - 20 %)では説明できない大きさである。 |
 図１９．He+/H+ と R の関係。白丸＝電波。黒丸＝可視。 右側の矢印＝マゼラン雲。左の縦棒は 2σ エラー。 |
 図１２．HIIR のイオン組成 |
 図１３．HIIR の元素組成 |
|
元素組成比の勾配 図２０，２１には O, N, S, Ne, Ar のイオンと全量の銀河中心距離変化を 表１２と表１３から採って示す。太陽付近の平均量と勾配の値は表１４に まとめてある。 S38 と S48 元素勾配はもし S38 と S48 を含めると大きな変化を示す。それらは多くの 相関から大きく外れているのでサンプルに加えなかった。これら二つは 前景の HIIR と誤認されているのかも知れない。しかしはっきりしたことが 分からないので、図には特別なシンボルで登場しているが勾配の計算には 使わない。  図２０．イオン組成の R 変化。矢印はマゼラン雲。 |
 図２１．各元素の総量の R 変化。白丸は S38 と S48 で、矢印はマゼラン雲の 二つの天体 N66 と 30 Dor. (a) と (b) の十字は Peinbert 1979 の決定。 (d) の十字は Talent, Dufour 1979. |
６．１．銀河系での組成変化６．１．１．局所的組成変化Te 誤差の影響図２１の散らばりが本当かどうかは興味ある問題である。Chevalie 1978 は 与えられた R における組成の差を生み出す原因を考察した。図２１に見える、 平均勾配の周りの散らばりは、 Te とライン強度比の観測値エラーで完全に 説明できる。例えば Te の 5 % エラーでさえ O, N 組成の散らばりの説明に 十分である。 |
太陽近傍 HIIR と太陽との差 では、オリオン大星雲と他の HIIR の組成はシグナスループ SNR の組成に近い。しかし、太陽と近傍高温度星の組成は 50 % くらい 高い。この違いの原因は不明である。 Meyer 1979 はダストが原因で HIIR の 組成が低くなるとした。しかし、Peinbert, Torres-Peinbert 1977 は O/H が トラペジウムからの距離によらず一定であることからそれに反対した。 |
 図２２．N/O 対 O/H. 白丸＝ S 38, S 48  図２４．{[OII](3727)+[OIII](4959+5007)}/Hβ 対 Te. 実線＝ Pagel et al 1979 の経験曲線。 白丸 = S 38, S48. |
 図２３．[OIII](4959+5007)/[NII](6548+6584] 対 Te. 実線＝ Alloin et al 1979 の経験曲線。破線＝Stasinska 1980 の Teff = 35000, 40,000 K モデル |
 図２５．酸素組成と電子温度の関係。実線＝ Pagel et al 1979 経験曲線。  図２７．酸素組成と ρ/ρo （ドヴォ―クルー半径で正規化した 銀河中心距離）との関係。実線= Pagel, Edmunds 1981 のデータへのフィット。 M31 データは Blair et al 1982. 銀河系では ρo = 14.3 kpc. |
 図２６．酸素組成と{[OII](3727)+[OIII](4959+5007)}/Hβの関係。 実線＝ Pagel et al 1979 経験曲線。黒点＝図２１a から採った。破線 はそのフィット。  図２８．銀河中心距離によるメタル量変化。点は図２１a から採った。 z = 25(O/H) とした。フィット曲線は a=対数表示に直線フィット。b=線形表示に直線フィット。c=Chiosi, Matteucci 1983 モデル。 |
|
（１）低い Te いくつかの HIIR では Te < 5000 K である。これは幅が 15 Km/s 以下の 再結合線の発見で疑い得なくなった。 （２）電波 Te と可視 Te の一致 電波で決めた Te と可視ライン比から決めた Te は一致した。電波で決めた Te とライン比 ([OII]+{OIII])/Hβ の間には良い相関がある。 （３）Te 勾配 Te の勾配 +433±40 K kpc-1 が見つかった。 （４）酸素勾配 酸素組成の勾配 -0.07±0.015 dex kpc-1 が定められた。 |
（５）窒素勾配 窒素組成の勾配 -0.09±0.015 dex kpc-1 が定められた。 （６）硫黄勾配 硫黄組成の勾配 -0.01±0.02 dex kpc-1 は酸素勾配より平坦である。 ネオンも同様に平坦のようであるが、アルゴンの勾配は酸素に近い。 （７）ヘリウム He+/H+ には勾配が認められない。 （８）散らばり 与えられた銀河中心距離での局所的な組成の散らばりは 20 % 以下である。 （９）内側勾配 内側で勾配が急という幾つかの証拠がある。 |
