| 内側銀河系の O-リッチ、進化した、中間質量星の一様なサンプルに対し、 力学分布関数を求めた。軸対称、２成分 Stackel ポテンシャルを用いた。 安定な２積分モデルは最初の３投影モーメントに関してデータを非常によく 再現する。しかし、中心部視線速度、中心スケール高、 |l|=[5, 15] でほぼ 完全に筒状の回転を再現できなかった。 | これらの特徴は銀河バーを示しており、３積分モデルで良くフィットする。 ２積分及び３積分分布関数を議論した。円盤の高年齢 AGB 星の観測分布を説明 するには、やや厚い円盤成分が必要である。この厚い成分は高銀緯での AGB 星 の運動を、薄い円盤より上手く説明する。AGB 星で見る限り円盤とバルジは力 学的に非常によく似ていて、同一成分と見做せる。しかし、バルジの 100 pc 以内は力学的に独立な成分である。 |
| 力学モデルには２種類ある。第１は N-体計算(Fux 1997) に基づく。第２は シュワルツシルド法である。ここでは第２の方法を採用して、中間質量星の 力学分布を探る。 |
このサンプルは古いバルジ星を含まない。
(OH 観測から中間質量星が抜き出せ るのか？ ) |
|
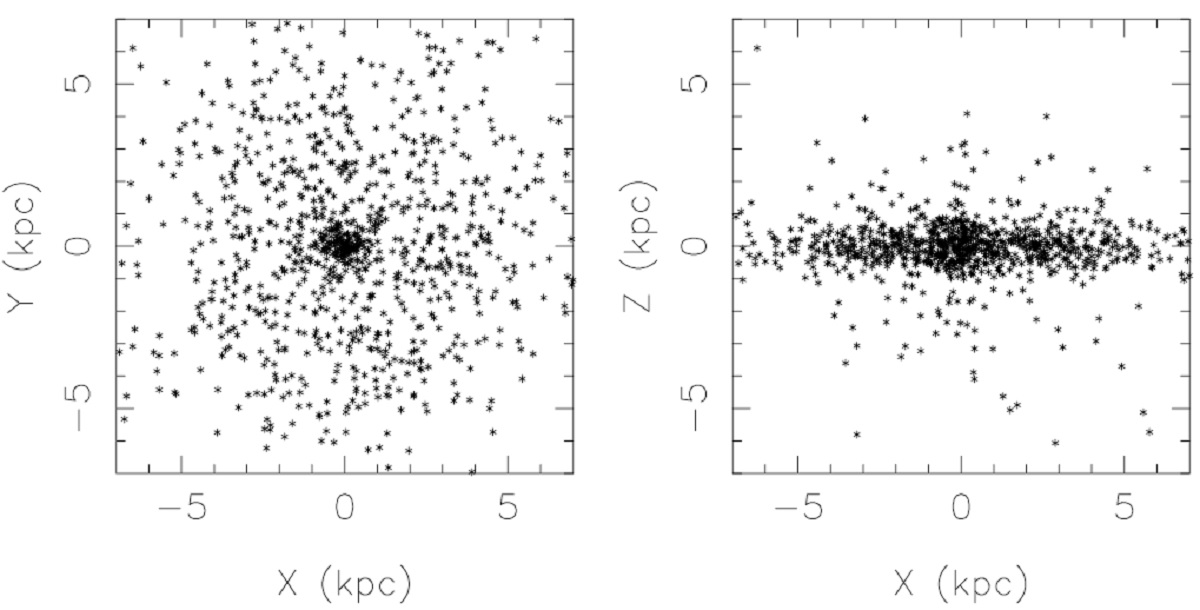
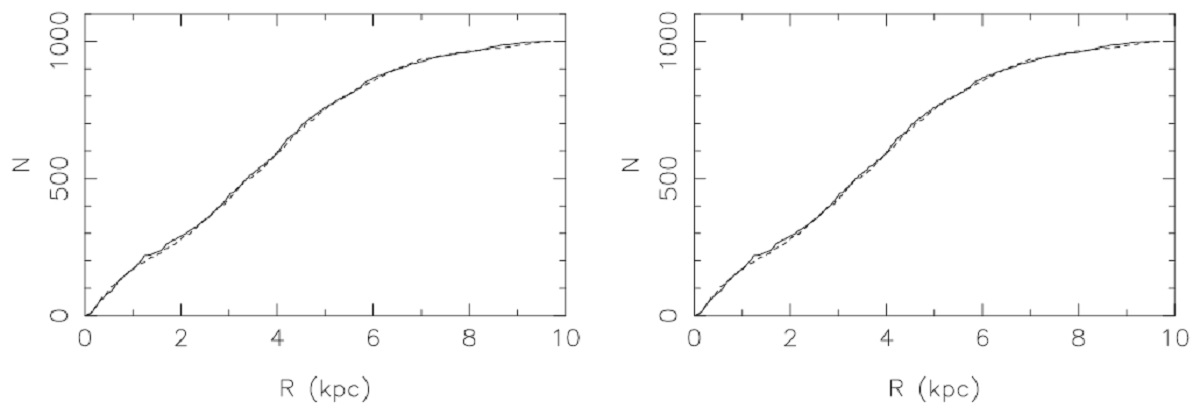
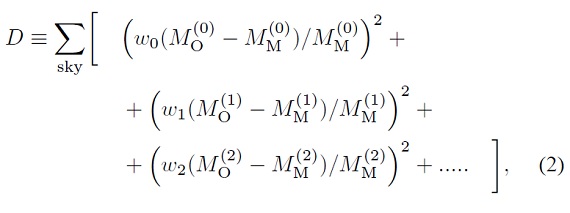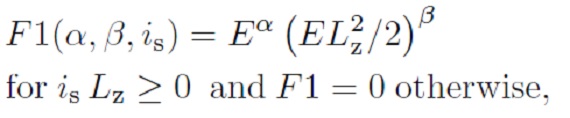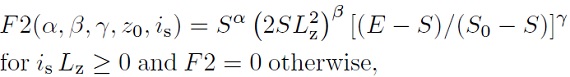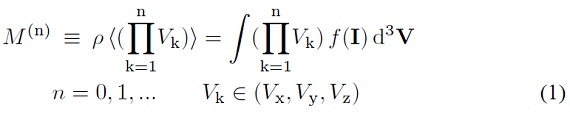
モーメント ジーンズの定理から、分布関数は多くとも３つの独立積分量の関数 f(Ii) で表される。この関数は （x、V) ６次元空間内の密度分布を与える。 ｆを速度空間で積分して、n-次モーメント M(n) を得る。  つまり、0-次モーメントは１個、1-次モーメントは３個、2-次モーメントは ９個ただし独立は６個ある。これらは位置 x の関数であることを注意する。 |
モーメント間の二乗距離 銀河系恒星サンプルの力学分布関数をモデル化する方法は Dejonghe 1989 が開発した。ここでは概要を述べる。 MO = 観測分布のモーメント、 MM = モデル分布のモーメントとする。 D = モーメント間の二乗距離は次のように与えられる。 D を最小にすることでベストフィットのモデルを得る。  |
|
OH/IR 星 OH/IR 星は年齢 0.5 - 0.7 Gyr Sevenster (1999) で、力学的には部分的に緩和した種族である。Frogel 1988 は質量分布のトレ ーサーでもある。サンプルは l = [-45, 10], |b| < 3° で、 AOSP = Australia telescope Ohir Survey of the Plane サンプルと呼ばれる 507 OH 源からなる。LSR は R = 8 kpc をポテンシャル中を円周運動している。 表１＝分散 何を言っているか全く理解できない。残念。 スムージング まず 1°x1°x30km/s のガウシャンカーネルで観測データに平滑化 を掛ける。次に、各星に対し、表面密度に応じて、空間カーネルが適用される。 ここも全く理解できない。 そして、天空上の各点で速度プロファイルに基づいて、平均速度と速度分散を 求める。最後に、表面密度、平均速度、速度分散を格子点上で計算する。 図１： 図１にはこうして得た表面密度を COBE/DIRBE 観測と比較した。 |
 表１．平均分散 |
|
Stackel ポテンシャル ３つの運動積分全てが解析的に与えられるので Stackel ポテンシャルを 採用した。具体的には軸対称な Kuzumin-Kutuzov (KK) ポテンシャルである。 こうして銀河は少数の軸対称で異なる厚みの成分の重ね合わせで表現される。 ここで焦点距離を等しくしておくと、双極座標系では分離可能になる。 Batsleer, Dejonghe 1994 はダブル S-KK ポテンシャルのパラメターを最適化 し、ダークハローと円盤の２成分銀河系モデルを与えた。表２にモデル パラメターを示す。 図２には AOSP サンプルの l-v 図を示す。表２にある２成分ポテンシャル で期待される回転曲線も載せた。BD2 ポテンシャルは中心に殆ど質量がなく、 内側銀河系の回転曲線（長破線）は勾配が緩い。さらにまた、l = [10,20] では v が大きすぎる。そこで、もっと中心質量を大きくしたモデルを考えた。 |
改良版ポテンシャル それらのポテンシャルパラメターを表２にしめす。 図３にはそれらの回転曲線を観測と比べた。 それでごたごたあって、 AX2 モデルが一番合うという結論。 |
|
２積分定数軌道族を二つ考えた。第１はバルジ的で有限の広がりに制限され る。第２は円盤的で縦方向に制限を受ける。第１成分は、  第２成分は、  ここに、E = 総エネルギーと Lz = 角運動量は軸対称系での古典的な二つの 積分量である。Lz を与えたときに、S = 高度 z0 まで達する軌道 のエネルギー、So = 銀河面内円軌道エネルギーである。 F1 と F2 の性質 F1 と F2 は Lz に関して偶関数である。パラメター is はその 為に導入された。is = -1 ：銀河回転方向の位相空間だけが満た される。is = 1 ：銀河反回転方向の位相空間だけが満たされる。 is = 0 ：可能な全位相空間が満たされる。 α は中心集中度を示す。β は回転の程度を表す。β が非ゼロ の時、密度分布はトロイダルになる。F2 に現れる z0 は 成分の垂直方向限界を示す。γ はスケール高を定める。 QP 法 QP プログラムは入力ライブラリーから可能なパラメターを読み込む。各成分に 対して、D が最小になる係数 C を定める。最小 D の成分を分布関数を形成する シリーズの第１に選ぶ。続いて、残り全ての成分で第１成分と組んだ時に D を 最小にするようにする。 |
 表４．入力ライブラリー。  図５．斜線の楔型＝そこで分布関数を積分してモーメントを得た。水平線 14 kpc までの観測を再現する。軸交点＝GC. 全ての R で視線との交点が二つあるわけで はないが、 R < 5 kpc は良好なようだ。 |
| ベスト２I分布関数(DHA)が表４の成分ライブラリーを用いて得られた。表５ に DFA の成分をその係数と共に示す。全 DFA は CnFn の和である。 図６に位相区間密度を示す。 |
 表５．ベストフィット分布関数 DFA の成分。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|