|
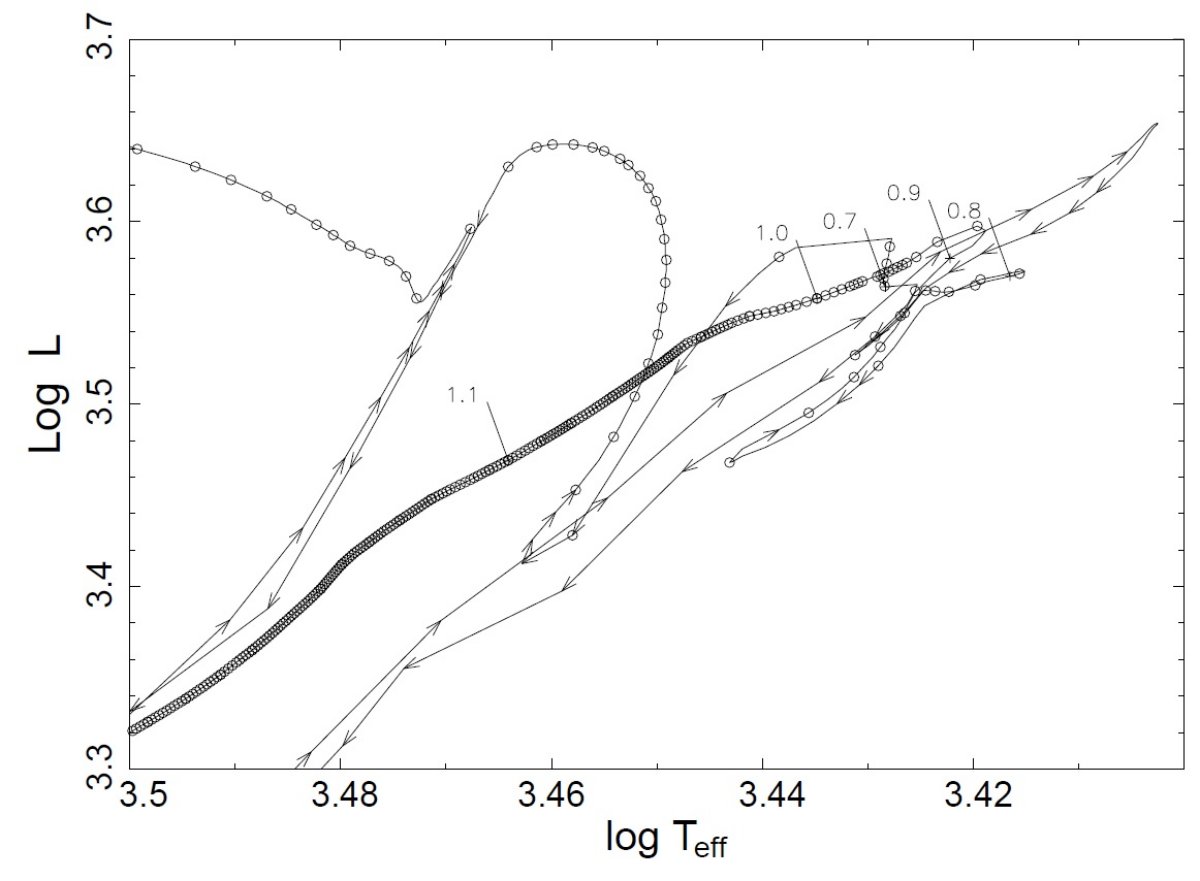
進化モデル AGB 末期、超星風が起こる時期の進化モデルを示す。計算は炭素星に対する脈動星風モデルに ダスト形成、輻射輸達、星風加速を組み入れた。 強い間歇的な質量放出 1.2 Mo 付近、0.2 Mo 巾の領域では、特別に強い間歇的な質量放出が起きた。これは明るい 炭素星の周りで見つかった 分離CO シェルの性質、つまり運動学年齢 1 - 2 × 104 年、数 0.01 Mo, 放出期間数千年以下、とよく合致する。 |
最終超星風 他の超星風モデルと違う点は、我々のダストで引き起こされる質量放出は恒星温度に 敏感 ∝ Teff-8 で、かつ最低光度が存在する。これらは、質量放出が 後の方ほど強力になっていくことを意味する。特に我々のモデルでは、AGB 先端最後の 2 - 6 × 104 年の間に、もし光度が log Lc ∼ 3.5 - 3.7 (Teff に依存)に近ければ、 CO シェルが作られ、その時期星の外層質量は 0.2 Mo 以下である。 |
|
超星風の存在 超星風を Renzini 1981 が言い出したのは、数 0.1 Mo の惑星状星雲を 104 年 以内に形成するには ≥ 10-5 M/yr の質量放出が必要だったからである。この 超星風に先立っては長いもっとおとなしい星風期があった。この描像は惑星状星雲の周囲に 冷たく、ダストと CO ガスに富んだ星周層(Kwok 1981)があることと一致する。また、 LPV で約 10-4 M/yr の質量放出(Knapp, Morris 1985, Winters et al 1997) があること もそれを支持する。 Bowen 型星風モデル 図1に見られるように、超星風は AGB 先端では進化の支配的要因である。ただ、質量放出率 自体は星の諸パラメタ―に影響される。したがって、星の進化と質量放出は一緒に計算する 必要がある。この分野の最近の研究、Vassiliadis, Wood 1993, Blocker 1995 のどちらも Bowen 型 の星風モデルを採用している。そこでは、周期ー質量放出率関係、つまり質量放出率は表面重力に 強く影響される関係にある。これは質量放出が次第にしかし力強く増加することを予言する。 |
Bowen 型星風モデルではダスト形成過程を組み込めない しかし、Bowen 型星風モデルでは複雑なダスト形成過程を組み込むことが出来ない。この過程は 温度、密度に極めて鋭敏な物理・化学反応である。 炭素星の分離シェル PN 形成の一般像は確立しているが、観測で明らかになった詳細の説明 には、より正確な AGB 先端部進化と超星風のモデルが必要である。 Olofsson et al 1990, 1993, 1996 は 3/65 炭素星に薄い、分離型 CO シェルを発見した。 それらは、運動学年齢が 0.3 - 13 万年で Mshell = 0.4 - 5 10-2 Mo であった。シェルの厚みは現在の値の二桁高い超星風が数千年の短期間続いたこと を暗示する。 熱パルス原因の超星風モデルの必要性 Olofsson et al はその原因が熱パルスではないかと述べているが、 これまでの超星風モデル (Vassiliadis, Wood 1993) は緩やかで単調な放出率の 増加を予言している。 |

|
新しい星風モデル ダスト加速による星風誘発メカニズムを組み込んだ、AGB 先端の ダイナミカルなマスロスモデルを作った。これは Sedlmayr 1994 が開始し、Fleischer et al 1992 は脈動炭素星の整合モデルを 作った。それらのモデルグリッドから Arndt et al 1997 はマスロス 式を以下のように求めた。 log(dM/dt) = 17.17 - 8.26 log (Te/K) + 1.53 logL -2.88 log M エディントン光度 上の式の M に対する強い逆依存性とその値は超星風を表現している。 その上、温度依存性が非常に強いことにも注意したい。これはダスト形成率の 温度依存性が非常に強いことから来ている。マスロスがダストに対する 輻射圧で誘発されるので、モデルには超星風に必要な最小光度が存在する。 Sedlmayr,Winters 1997. このエディントン光度の正確な値は実際のダスト オパシティに、従って Te によるが、典型的な値は M = 1 Mo, log Te = 3.5, log Lc = 3.7 である。 この論文でやったこと この論文では、この脈動、ダスト形成誘導型超星風モデルを AGB 先端進化 に応用した計算を報告する。その結果、明るい炭素星の周りに発見された 分離型 CO シェルを作り出すような短期間の強い質量放出現象が再現された。 |
進化コード Eggleton 1971, 1972, Pols et al 1995 の、 パラメタ―化した対流ミクシングを組み込んだ最新進化コードを使った。 しかし、最新の進化コード一般に起こることだが、有効温度が観測より 高く出てしまう。これを直すため、AGB 進化に伴いじわじわと α を 低下させる細工をした。 α = 2.0 + 0.17 (log(g/go)+2.5) この式では log g(cgs) = -1 で α = 1.5 となる。 熱パルスタイムスケールが短くなる こうして、計算時間を短縮できたので、タイムステップを稼げ、 マスロスが 10-6 になるまでは 熱パルスの効果も 無視できた。 Vassiliadis, Wood 1993 と比べると最後の頃の 熱パルスのタイムスケールは短い。しかし、 Wagenhuber, Weiss 1994 を見ると、熱パルスタイムスケールが短くなっており、おかしくはない。 マスロス史 現実的なマスロス史を与えるために、AGB 前とコアヘリウム燃焼期には われわれはReimers 1975 の経験的マスロス式 η = 4×10 -13 を使用した。 AGB 期には de Jager et al 1988 を採用 した。最後に、 AGB 先端、 log L = 3.5 - 3.6 ではここで示すモデル に Arndt et al 1997 のマスロス率を併用して使った |
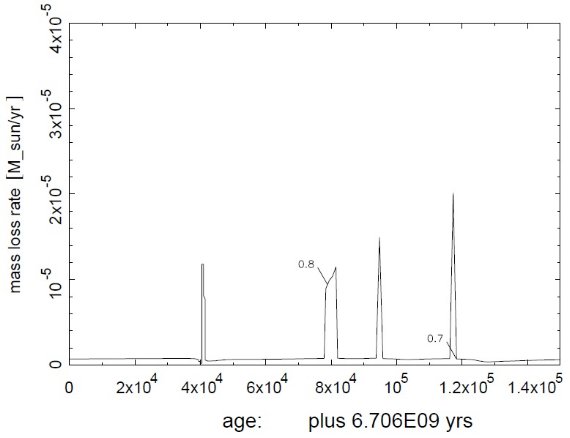 図2.AGB 初期質量 1.15 Mo の最終マスロス史。数字はその時点での質量。 こういう炭素星が臨界高度 Lc に達すると、短期間の爆発的超星風が起き、 分離シェルを形成する。 星の温度、光度への強い依存性から超星風が生まれる。 計算結果の表示として、X = 0.70, Y = 0.28, Z = 0.02 AGB 初期質量 1.15 Mo(図2)、1.25 Mo(図3)、1.4 Mo(図4) に対する最終マスロス史 を示す。最後の 105 年、超星風の以前までに AGB 上では 0.3 Mo が失われ、残りの 0.2 - 0.4 Mo が超星風で吹き飛ばされる。 超星風は星の温度、光度に強く依存するので、熱パルスに伴い、大きく 強調された星周シェルが作られる。 熱パルスと星風の関係 熱パルスの間、質量放出は一度低下する。それから急激に 1‐2 桁大きく なるが、それは 100 年程度の極端に短い期間に起こる。この計算結果は 橋本ら 1998 の観測と良く合う。 3000 年以下の爆発的な星風 熱パルスの放出エネルギーが少し遅れて表面に達し、光度があがり、表面 温度が低下する期間、質量放出率は高い値を維持する。 AGB 質量が、 したがって外層質量も、下がると、この質量放出率の跳ね上がりは強まる。 その上、AGB 最後の数万年、光度が Lc に近く、外層質量が 0.2 Mo しか 残っていないと 3000 年以下の爆発的な星風が起きる。それは、外層質量が 低下し、有効温度が上がって停止する。 放出率が低い期間にはこのような星は 再び中心まで見通せるようになり、数 10-2 Mo の薄いシェルが 周りに見える。運動学年齢は 104 年程度であろう。これは Olofsson et al 1993 の発見に合致する。 我々の超星風モデルは星風、シェルの速度として 10 - 20 km/s で C/O 比と共に増加する傾向を予想する。これは観測された CO シェル速度、 13 - 20 km/s、の範囲内にある。また、進化タイムスケールと、したがって 分離シェルのある星と、超星風期以前で、分離シェルのない星との比の予想 値は 1 対 10 である。さらに、そのような星の質量範囲の制限による選択 ファクターを 2 - 3 とすると Olofsson et al 1990 の得た 65 サンプル中 約 3 星という値になる。 ( サンプルとして全炭素星を とったら?) |
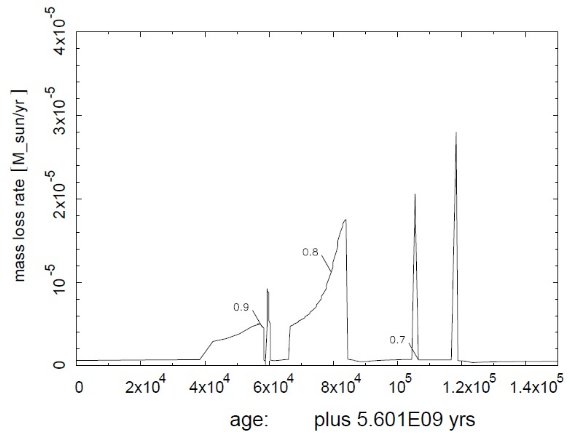 図3.AGB 初期質量 1.25 Mo の最終マスロス史。数字はその時点での質量。 超星風の前後には強いマスロスの増減が見られる。 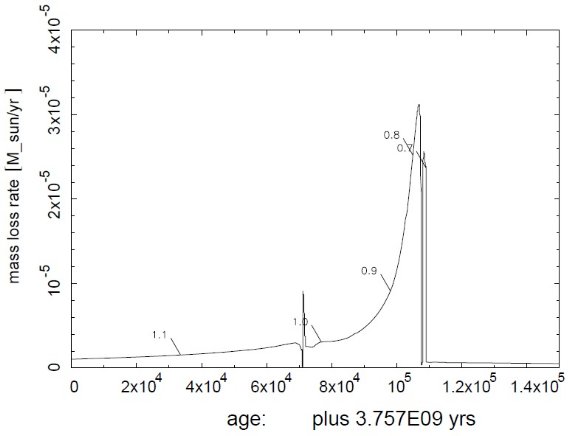 図4.AGB 初期質量 1.4 Mo の最終マスロス史。数字はその時点での質量。 星質量が大きくなると、超星風期のマスロス変動幅は減少する。 初期 AGB 質量 1.1 Mo 以下の炭素星は超星風に達しなかった。これらの 星では光度が十分高くなる以前にコアが露出してしまう。逆に 1.4 Mo 以上の星では、 AGB 先端光度は Lc を十分に超え、質量放出の変動は そう大きくない。どちらの場合も分離シェルを形成しない。これにより、 分離シェルを形成する星の初期質量は狭い範囲に制限される。シェル形成時 の星質量の巾も狭く 0.7 - 0.8 Mo である。 |
|
観測との一致 この計算結果は星の最終進化の一般論と観測された超星風 とに良く合っている。初期質量 1.3 - 1.5 Mo で、初期 AGN 質量 1.2 - 1.4 Mo の星は超星風により、 2 - 4 104 年の間に 0.2 - 0.4 Mo を失う。 これもまた、可視光では見えない長周期変光星の星周雲が質量放出率 数 10-5 Mo/yr, 運動学年齢 数 104 年、シェル質量 数 0.1 Mo であることと合致する。進化の最後には我々のモデルは 最終質量 0.58 Mo となったが、これは Weidemann 1987 の関係に合う。 ( 一致の対応があいまい。) |
残る問題は、オパシティの改善と有効温度の決定である。しかし、 超星風の全体像は大きくは変わらないだろう。もう一つは 対流ミクシング理論の扱いである。早期の熱パルスによる ドレッジアップを取り込むと C/O 比は変化する。これは C-リッチ 超星風の開始に影響する。ただ、質量放出率自体は C/O 比に あまり依存しない。 |