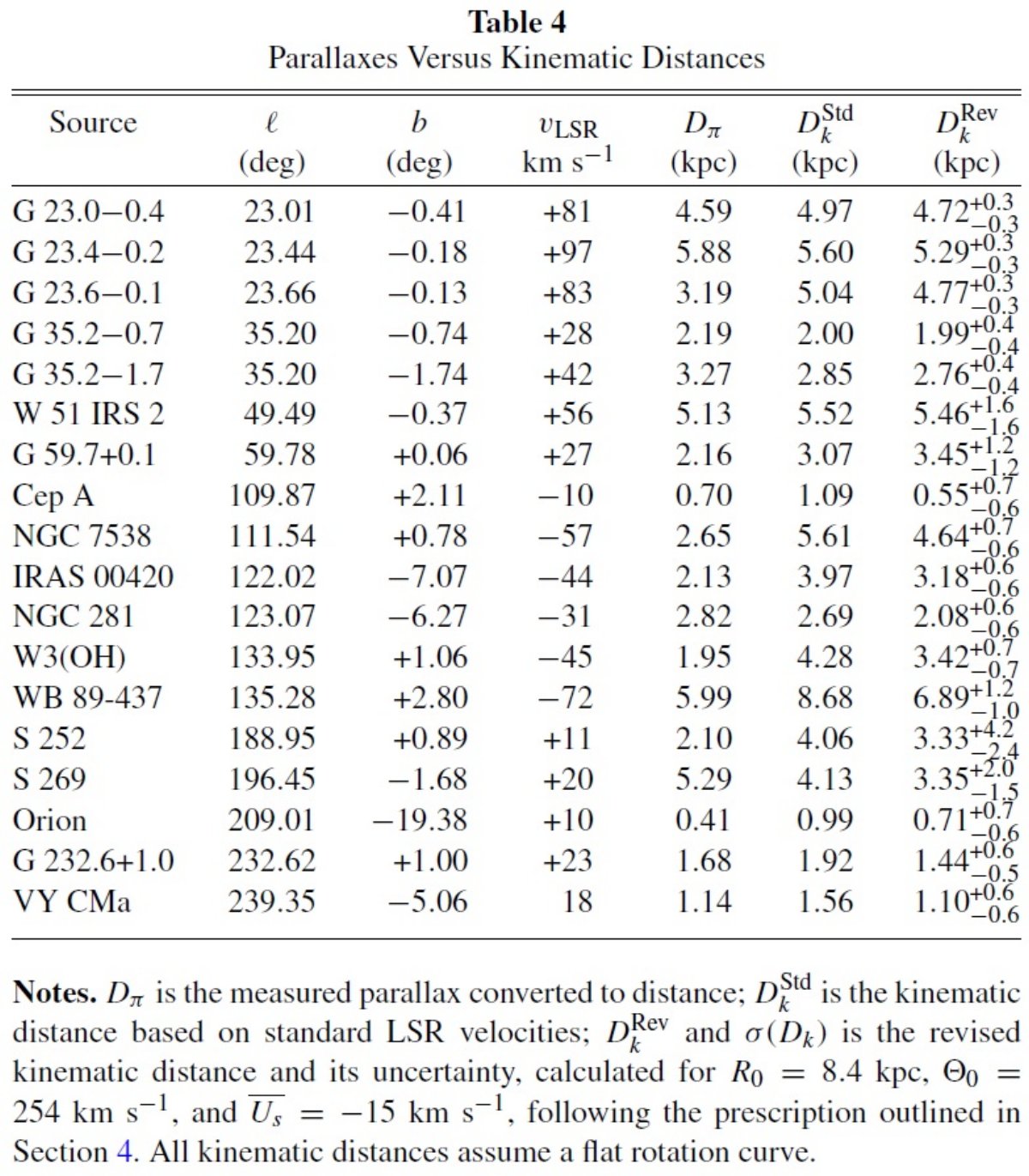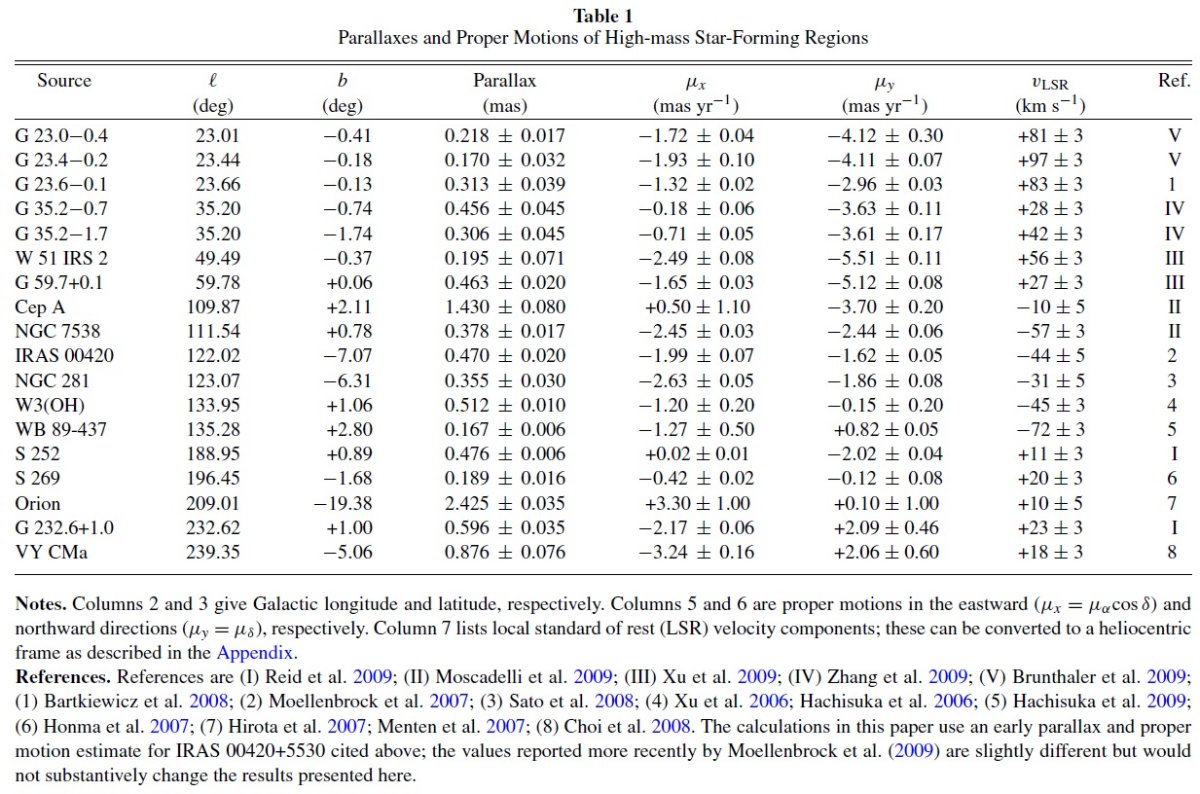
| VLBA と VERA を用いて星形成領域内メーザーの固有運動と視差を測っている。 18個のメーザーに対する初期結果はそれらを幾つかの渦状腕の上に位置させた。 ペルセウス腕のピッチ角=16°±3° は2本腕よりは4本腕に 合う。星形成域が円運動から予想されていたよりも、平均して 15 km/s 遅い 速度であることを見出した。また、 Ro = 8.4±0.6 kpc, Θo = 254±16 km/s, Θo/Ro = 30.3±0.9 km/s/kpc である。 | データは回転曲線がほぼ平坦かやや上向きであることを示す。一般に運動距離 は大き過ぎる。いくつかの例ではファクター2以上となる。Θo/Ro を IAU 推奨値の 25.9 km/s/kpc から 30 に変えると運動距離と視差との一致は 向上する。運動距離を更新する処方を示す。回転曲線はM31のものと似ており、 二つのダークマターハローの質量が同じくらいであることを示唆する。 |

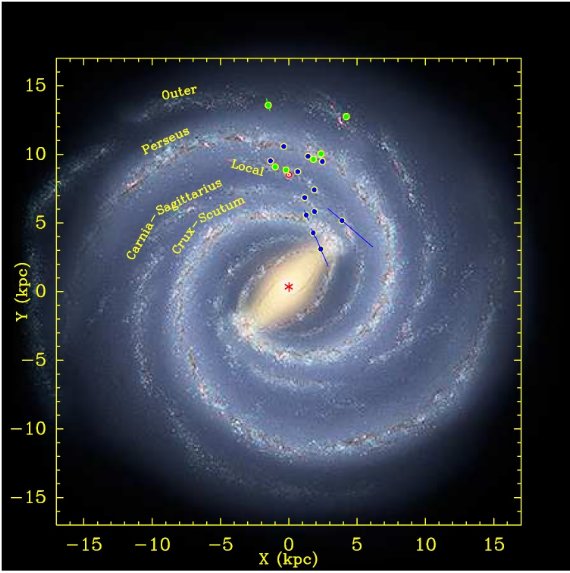 図1.濃い青の丸=メタノールメーザー源。明るい緑丸=H2O, SiO メーザー源。GC=(0, 0) 太陽=(0, 8.5). |
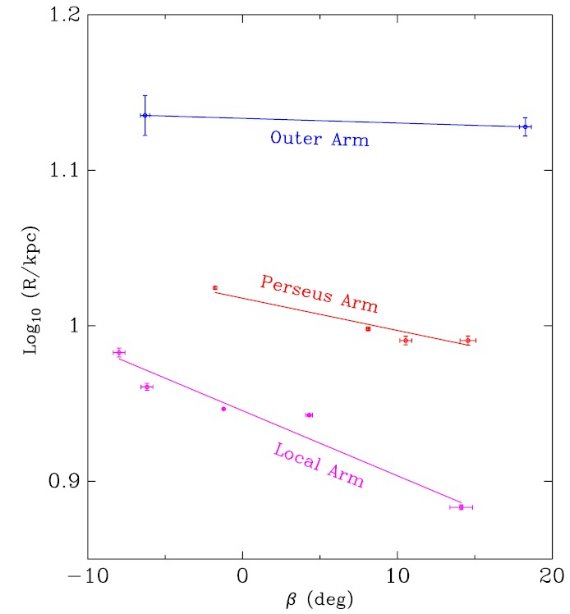 図2.β = 銀河中心から測った方位角。 フィット直線の勾配を A とすると渦状腕のピッチ角 θ は A = tan θ である。 |
|
バー端付近 銀河中心方向のメーザー源 G23.0-0.4, G23.4-0.2, G23.6-0.1 はクルックス・ ケンタウルス腕のメンバーのようだが、北天からは低光度観測になる上、遠方 なので誤差が大きい。 ノルマ腕か 3 kpc 腕の可能性もある。というのはこの 方向はバーが終わり腕が始まるあたりだからである。 サジタリウス腕 G35.2-0.7, G35.2-1.7, W51IRS2 の3つは多分カリーナ・サジタリウス腕で ある。太陽からは 2.5 koc 離れている。 ペルセウス腕 5メーザー源、S252, W3(OH), IRAS00420+5530, NGC281, NGC7538 は明らかに ペルセウス腕をなぞっている。それらは (l, D) = (189°,2.10kpc) の S252 から(112°, 2.64kpc) の NGC7538 へと連なっている。S252 は膨張スーパー バブルに随伴して腕から少し離れているらしい。Sato et al 2008. |
アウター腕 VERA と VLBA で観測された S269(196°, 5.3 kpc) と WV89-437 (135°, 5.9 kpc) はペルセウス腕の向こう側にあり、アウター (シグナス)腕をなぞり始めている。 局所(オリオン)腕 残りの G232.6+0.1, VY CMA, オリオン星雲、 Cep A, G59.7+0.1 は、 局所(オリオン)腕天体である。この腕はカリーナ・サジタリウス腕とペルセウス 腕の間の枝腕のようである。太陽はこの枝腕の中か近くにある。我々は l = 60° でカリーナ・サジタリウス腕の近くにある G59.7+0.1 から l = 233° でペルセウス腕近くにある G232.6+1.0 へとこの腕をつないでいく。 |
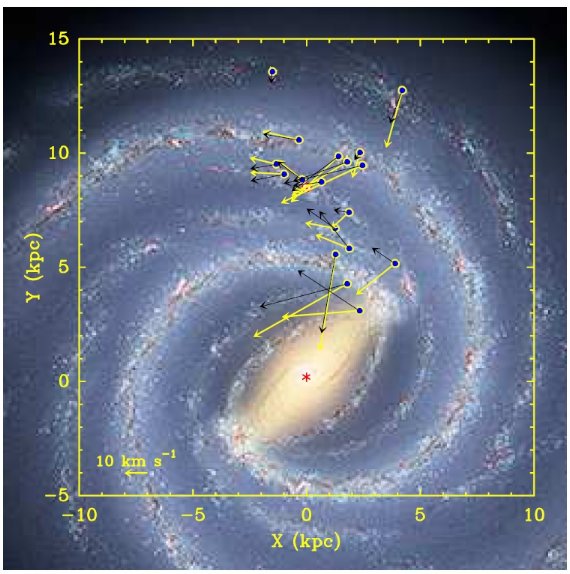 図3.銀河中心の周りを回転する参照系から見た HMSFR の特異運動。 上から見た銀河系は時計回りに回転している。黄色矢印= IAU 半径と 回転速度 (Ro=8.5kpc, Θo=220km/s)と平坦回転曲線の場合。 黒色矢印=(Ro=8.5kpc, Θo=254km/s)の場合。二つの違いは HMSFR が銀河系回転より遅く回っているという結論は Θo の 値にあまり影響されないことをしめす。 |
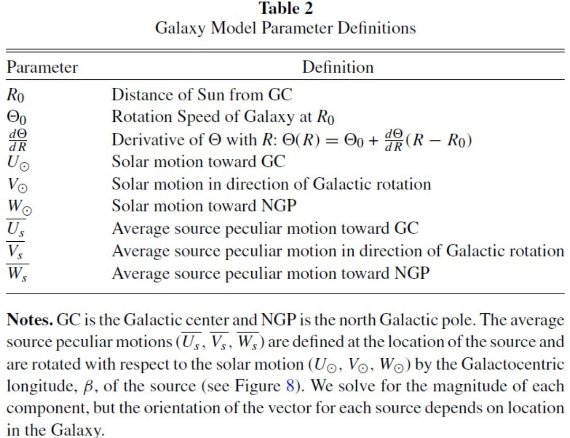 表2.銀河系モデルパラメタ―の定義 (特異運動=星の速度ーLSR速度、 だが、そこに "銀河中心の周りを回転する参照系から見た" という 言葉をわざわざ入れるのはどうしてなのか?銀河系の周りを回っている太陽 から観測した値であることを意識してか?ただ、どの慣性系に乗っていても 速度差では相殺される。) |
3.1.銀河系3次元運動銀河系モデルの第1近似として、円盤回転速度 Θ(R) = Θo 一定 と考える。表1の18天体データを解いた結果が表3のフィット1である。 自由度 70 に対する χ2 = 267 は大き過ぎ、この2パラメタ― モデルが不十分であることを示す。図3には Ro = 8.5 kpc に対し、Θo = 220 km/s(黄色)と 254 km/s (黒)の場合の特異運動を示す。どちらも明らかな 系統的な特異運動の傾向が見える。平均して星形成領域は銀河系回転速度から 15 km/s 程度遅い動きを示す。この結論は Θo にあまり影響されない。 これは、尾を引いて動く渦状腕の衝撃波面に分子ガスが衝突して星形成が引き 起こされるという考えで説明される。3.2.銀河系基本パラメタ―そこで、HMSFR の LSR からの運動のズレの3成分平均値をパラメターに入れて、 フィット2を得た。その結果は表3にあるように、67 自由度に対し χ2 = 112 と大幅な改善が得られた。更にズレの大きな NGC7538 と G23.6-0.1 を除いてフィット3、自由度59に χ2 = 65.7 を得た。3.3.回転曲線フィット3に速度勾配を加えて最少二乗で解いた結果がフィット4だが、 Ro と Θo の相関係数が 0.90 と大きい。そこで、 S269 と WB89-437 を落として、等々の処置をした結果がフィット5,6,7 である。明らかに 将来データが増えると良い結果が期待できるだろう。 |
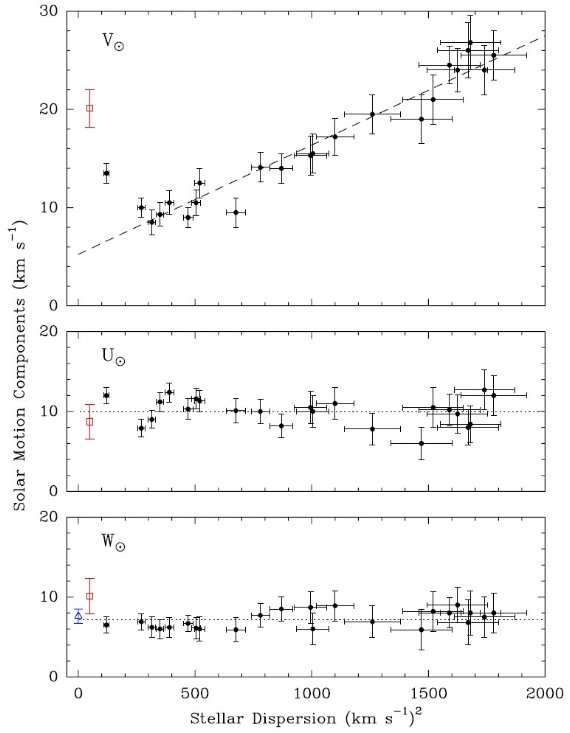 図4.ヒッパルコスデータから決めた太陽運動。上:Vo=銀河回転方向成分 中:Uo=GC方向の速度成分。下:Wo=銀河北極方向速度成分。 (Denhen, Binney 1998 図4より) |
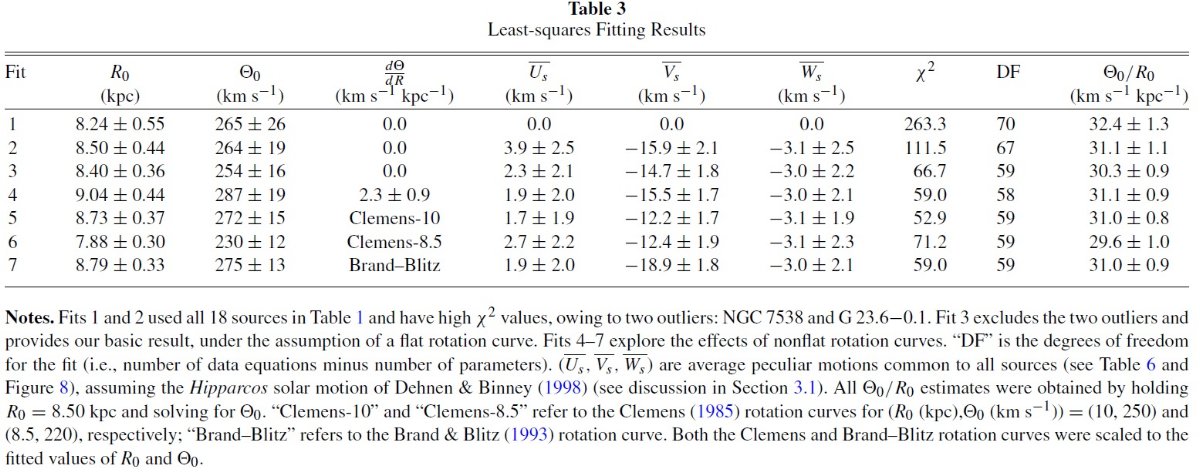
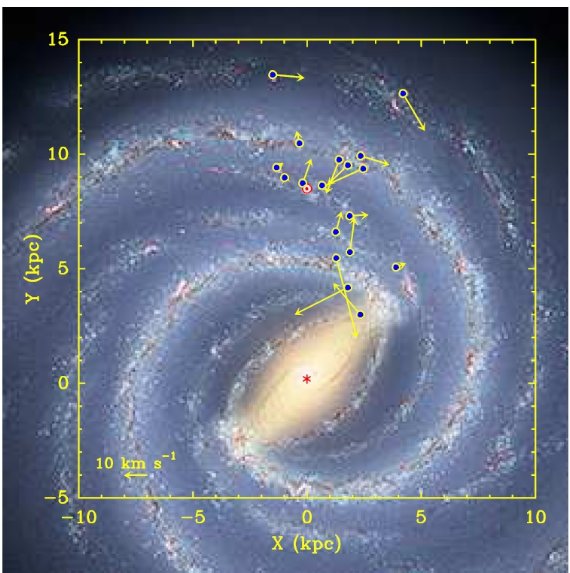 図5.フィット3に合わせ、HMSFR の運動に含まれる V=-15 km/s, U=2 km/s の動きを補正した後の固有運動。Ro = 8.4 kpc, Θo = 254 km/s. |
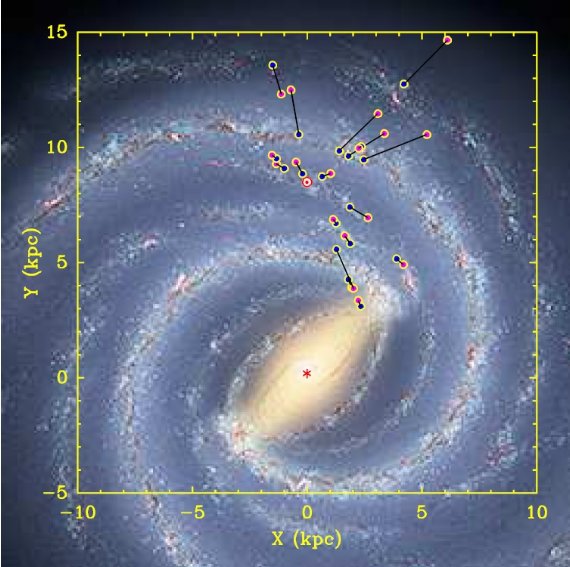 図6.濃紺丸=視差距離、マゼンタ丸=運動距離による HMSFR の位置。 運動距離は Ro=8.5kpc, Θo=220 km/s を仮定して決めた値。 |
|
図6では運動距離が視差距離よりも大きく出る傾向にあることが判る。
13/18 天体で運動距離の方が大きい。3例では倍以上の距離となっている。
前に調べたように HMSFR は回転速度が遅れる。そこで、 (1)LSR 速度に古い標準太陽運動を戻す。 (2)太陽運動の「最良値」を加えて LSR 速度を改訂する。 (3)速度回転成分から -15 km/s を引く。 |
(4)視差測定値と整合する Ro=8.4 kpc, Θo=254 km/s を使い、
運動距離を決める。
(5)運動距離の不定性を計算する時は、速度の 7 km/s 不定性を加える。 表4には、視差距離、(古い)運動距離、改訂運動距離を示す。距離差の 平均値はゼロに近く、そのばらつきは小さい。しかし、ズレは期待したほど 小さくならなかった。これは太陽運動に標準値 Vo =15.3 km/s を使っている ためで、ヒッパルコス太陽運動の Vo = 5.25 km/s を用いるともう少し 良くなる。 |