Luminosity Function of Soloar Neighborhood OB Stars


Reed
2001 PASP 113, 537 - 542



　アブストラクト

　太陽近傍 OB 星の光度関数を、mpg ≤ 10 mag の 2600 星から導いた。サンプル星の絶対等級により距離・完全性関係が変化すること と、銀河面に垂直方向の密度変化も考慮した。 　得られた光度関数は Humphrey, McElroy が以前得たものと -7 > Mv > -4 で良い一致を示した。銀河面上での数密度として、 9.1 × 10-7 stars pc-3 を得た。太陽円以内では 19,000 個となる。太陽から 2.5 kpc 以内に予想される 20 Mo 以上の星の数 636 は Garmany et al が与えた 424 個にくらべ 50 % 大きい。彼らが推定に用いた サンプルは不完全だったためであろう。

　１．イントロダクション　

　光度関数

　光度関数 φ(M) = 絶対等級 M 当たりの星数密度は、通常 M - log φ(M) の形で表示される。McCuskey 1965 によいレビューがある。過去 20 年間、 OB 星と様々な温度の超巨星の研究は IMF に注がれてきた。しかし、 OB 星のみ の光度関数に関しては Humphreys, McElroy 1984 しかない。

　サンプル選定の困難さ　

　それにはいくつかの理由がある。まず、数が少ないため、数 kpc 遠方まで サンプルを求める必要がある。すると、変動する星間吸収のため体積制限サンプル を作ることが困難である。また、銀河面上方のサンプルを含めると、スケール高 の効果を配慮する必要がある。 		論文の目的　

　それにも拘らず、データの集積が進んだ現在、OB 星の数についてまとめておく べきであろう。Massey 1998 が述べたように、大質量星では IMF は LF に対して 鋭敏ではないので、 IMF を導く試みは行わない。

　手続き　

（１）ある見かけ限界等級までの星の見かけ等級とスペクトル型を調べる。　
（２）スペクトル型から絶対等級を決める。
（３）見かけ等級限定サンプルを体積限定サンプルへと変換する。 それには、見かけ上最も暗く、固有光度最低(和か積か不明？)の星の距離を truncate するか、または最も低光度の星の空間密度が、見かけ上最も暗く、固有 光度最大の星の距離まで一定と仮定して、暗い星の数をそこまで外挿するかである。
（４）他の方法は、あまり用いられて来なかったが、距離分布を求めて、絶対等級ごとに 完全性保障距離を定めることである。この方法は原理的には全サンプルの情報を 用いる点では優れている。
この論文では (4) の方法を採用する。

　２．サンプル選定　

　LS-星の文献データ　

　銀河系 OB 星の最も一様な調査は Case-Humburg の北天と南天のサーベイであろう。 合わせて LS-カタログと呼ばれる 7 篇の論文には、 12,522 個の星が載っている。 範囲は mpg ≤ 13 mag, b = [-10, +10] である。WR 星、 A, F, G 超 巨星などが紛れ込んでいるとは言え、 LS 天体の大部分は B9 までの巨星と超巨星、 B2 までの主系列星である。私はここ数年、 LS-星の　MK-分類と UBVβ 測光値 を文献から集めてきた。mpg ≤ 10 までの星の 70 % に対しては データが揃ってきた。

　完全性限界

　LS 星の数は暗くなると、 Mpg = 11.5 までは急速に増大する。しかし、 カタログが完全なのは Mpg = 10.0 までである。この限界値はこの 論文でも採用される。 Mpg ≤ 10 で b = [-10, +10] の LS-星は 2825 個ある。ただし、OB 星でないものは除いた。 		絶対等級と固有カラー　

　これら 2825 星の殆どには UBV 値が付いている。しかし、分類は 2107 個にのみ与えられている。うち 1955 個 = 1955/2825 = 69 % の分類は絶対等級を与えられるレベルの内容である。固有カラーと 絶対等級は Turner 1980, Schmidt-Kaler 1982 から採った。

　スペクトル型　

　スペクトル型の多くは Morgan, Code, Whitford 1955 (720 星), Garrison, Hiltner, Schild 1977 (483 星) から採った。他は Michigan Spectral Survey (230 星), Hiltner 1956 (59 星）, Massey et al (41 星）などである。 　

　３．等級と距離の完全性限界　

　LS カタログの完全度限界等級　

　LS カタログは何等まで完全度が保障されているだろうか？ Massey et al の論文と較べてみた。彼らの 21 個の星団・アソシエイション星で LS カタログ基準に合致する B ≥ 10.1 の星 98 個中 LS カタログには 89/98 = 91 % が載っていた。一方、mpg ≤ 11.5 (B ≤ 11.6) に下げると 184/254 = 72 % が LS カタログに載っていた。したがって、 mpg = 10 を 90 % 検出等級としてよいだろう。

　LS カタログの完全度限界距離　　

　この問題を考えるため、図１に R = 3.1 を仮定して求めた距離の分布を示す。Vo = 赤化補正した見かけ等級として、

　　　log r = 0.2(Vo + 5) - 0.2 Mv

図１の上輪郭は、星間減光がない星が Vo = 10 になる距離をつないでいる勾配 -0.2 の直線であろう。破線は　log r = 2.8 - 0.2 Mv であり、上式の Vo = 10 に対応する log r = 3 - 0.2 Mv と殆ど重なる。
　図１で log r > 3.6 (r > 4 kpc) のサンプルが少ないことにも注意せよ。 　 Hakkila et al. 1997 の３次元減光マップによると、銀河面平均減光率は 1.5 mag/kpc である。 銀河面から上の星も考えると、 1.08 mag/kpc が良い値である。 その減光で log r = 3.6 が光度大の星の限界距離となる。 結論として、完全度保障の限界距離は

　　　　　log r = 3.6　　　　　　　　(Mv ≤ -4)

　　　　　log r = 2.80 - 0.2 Mv　　　(-4 ≤ Mv ≤ -1)

　絶対光度未定の 870 星をどうする？　

　絶対光度未定の 870 星をどうするかという問題が残る。２段階の対策を採った。
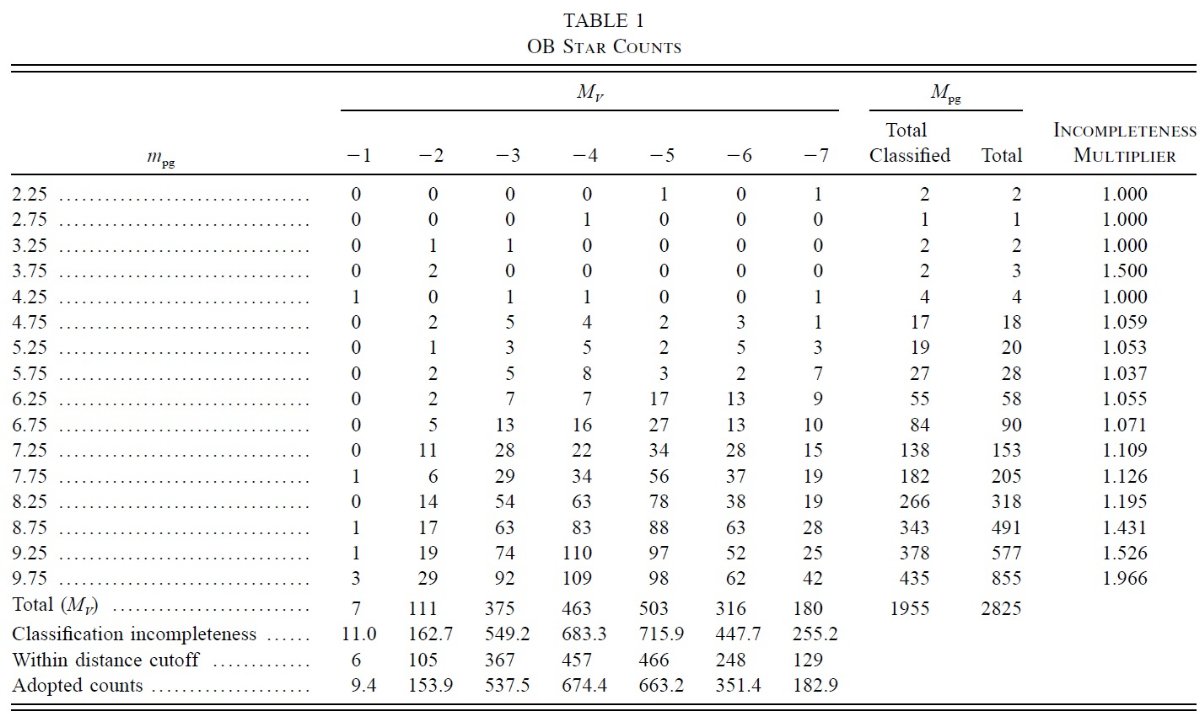
（１）表１のように、1955 星を mpg 0.5 等、Mv 1 等の格子に分ける。 最後から第４行は各 Mv の総数、最後から第２列には各 mpgの総数、 第３列には各 mpg でスペクトル分類ありの数が載っている。第１補正は 分類有りの星の分布にしたがって、各 mpg 内の分類なしの星を振り分け ることである。最終列にその比率を載せた。表の最後から第３行には各 Mv　毎に 補正数を載せた。 （２）距離限界の補正を行うために、各 Mv 毎に限界距離内にある分類有りの星の数 を数え、表の最後から２行目に載せた。この数で補正を行う。

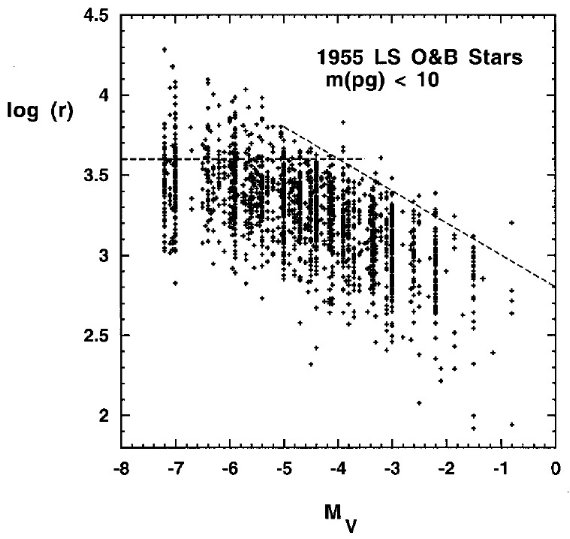
図１．1955 個の mpg CH-カタログ星の距離と絶対等級の分布。 破線＝サンプルの距離限界として定めた。



総数　

　こうして、合計サンプル数を 2573 個とした。これは Garmany et al 1982 の 6 倍であり、サイズとしては Humphreys, McElroy 1984 の 3273 個に匹敵する。



表１．OB 星の計数

　４．ＯＢ星の光度関数　

　計数体積の計算　

　表１の Mv 各枠の中央値を代表値とし、その限界距離 rcutoff 内体積 V = (4π/3)sin(bmax)rcutoff3 から密度を求める。bmax = 10° である。こうして求めた密度 を "Direct" と名付け、表２に載せた。

　スケール高を考慮　

　しかし、 "Direct" 密度は太陽付近の光度関数としては誤解を招く。 と言うのは、遠方では 10° はスケール高の数倍となるからである。 例えば、 r = 1 kpc では b = 10 が z = 170 pc になる。そこで、z-方向の 密度変化を、

　　　　　ρ = ρo exp(-|z|/h)

と仮定する。その場合、星の数は

　　　　　N = 2πρ0{R2h(1 - e-x) - 2h3(csc b)2 [1 - e-x(x2 /2 + x +1)]}

ここに、x = R(sin b)/h である。 　この式を表１の星計数と較べると銀河面上密度 ρ0 を 求められる。それを表２と図２に示した。 図２の特徴　

　図２で注意すべきは、

（１）Mv ≥ -3 でサンプル数が不足している。これは B1 V 星に 対応する。

（２）Humphreys, McElroy 1984 との一致が良い。これは -7 < Mv < -3 の星は実質的には全て OB 星であることを示す。


表２．OB 星の空間密度

　Garmany et al 1984 との比較　

　Garmany et al 1982 は O-型星のみを扱った。彼らは 2.5 kpc 以内の 20 Mo 以上の星はそのサンプル 424 星で完全と主張している。20 Mo は Mv = -4.2 に相当する。我々の LF は 2.5 kpc 以内に 636 星を予想する。恐らく Garmany et al 1982 のカタログは」不完全なのであろう。

　銀河全体の OB 星の数　

　図２の LF が銀河全体で成立し、スケール高一定と仮定して、
(動径密度変化無視？ )
積分すると、Ro 以内の -7 ≤ Mv ≤ -1 の星の総数として、

　　　　　 N = 2πρplaneRoh

が得られる。ρplane = 10-7pc-3、 Ro = 10 kpc, h = 45 pc として、 N(10kpc) = 25,800 個、N(8.5 kpc) = 18,600 個となる。 Case-Humburg サーベイの完全度は 50 % である。
(銀河面の半分を被ているとは思えないが？)



図２．明るい星の光度関数。白丸＝ Humphreys, McElroy 1984 （Mv = -5.5 まで完全。）より。菱形＝ McCuskey 1965. 黒丸＝本論文でスケール高 45 pc を仮定。