On the Absorption and Emission of Light by Interstellar Grains


Purcell
1969 ApJ 158, 433 - 440



　アブストラクト

　クラマース・クロニッヒ関係を星間空間に適用　
　クラマース・クロニッヒ関係を星間空間媒質に適用した。 ここでは星間空間は回転楕円体グレインが疎らに散らばる真空空間と考える。 この関係を用いると、減光曲線全体に渡る積分は星間媒質の静誘電率と関係する。 これは直ちにグレインが星間空間中に占める体積比の下限を与える。 		グレインの遠赤外放射率　
　この同じ方法をグレインの遠赤外放射率に適用した。低振動数振動子をむやみに 押し込んでグレインの低振動数放射率をかってに増加させることはできない。 得られる放射率の上限が導かれ、それを使って与えられれた半径と形状の グレインの熱平衡温度の下限値が定まった。


　１．イントロ　

　クラマース・クロニッヒ関係の応用の目的　
　この論文ではクラマース・クロニッヒ関係（分散関係）を応用して、次の疑問に 制限を与える。
（１）星間減光を説明するのに必要な個体媒質の量
（２）星間空間におけるグレインの平衡温度

　クラマース・クロニッヒ関係の説明　
　クラマース・クロニッヒ関係は電気感受率の実数部と虚数部を結びつける。磁気双極子 による吸収放射を無視すると、我々は複素電気感受率 χ のみを考慮すればよい。

　　　 χ(ω) = χ′(ω) - i χ"(ω)

出発点になるのは次のクラマース・クロニッヒ関係式である。

χ′(ω1) - χ′(∞) = 2 ∫ ∞ ωχ"(ω)dω
π 0 ω2-ω12


χ′(∞) = 0 として構わない。次に、ω1) = 0 とおくと、上式は吸収率積分と静電気感受率を結ぶ式となる。

χ′(0) = 2 ∫ ∞ χ″(ω)dω
π 0 ω


静誘電率は 1+4πχ′(0) で与えられる。この式から明らかなように、 静誘電率のいかなる制限も積分吸収率に何らかの制限を加える。

　星間空間への適用　
　上の式を星間空間に適用するに当たり、グレインの組成物質そのものではなく、 星間媒質をマクロにとらえる。つまり粒子の散らばる真空空間を巨視的に見る。 グレインは回転楕円体と考える。対称軸方向の反軸長を a, 赤道方向の 半径を b とする。軸の向きはでたらめである。単位体積当たりグレイン数密度を N とする。グレイン物質の静誘電率は εg とする。

回転楕円体粒子を含む真空空間の静電感受率 F　
　粒子を含む空間の静電感受率 χ′(0) は

　　　χ′(0) = N a b2 F(a/b,εg)

で与えられる。

　球形粒子の静電感受率　
　粒子が判型 r の球の時、

χ′(0) = εg -1
εg + 2


となる。さらに、伝導体球では上式で εg = ∞ とすればよい。

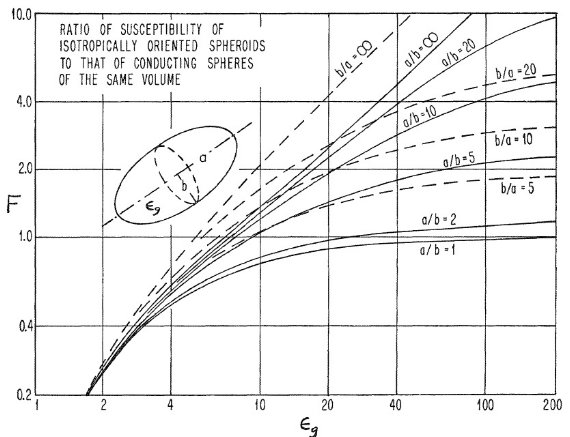
図１．F(a/b, εg ) 対 εg プロット。 F は、でたらめ方向を向いた回転楕円体粒子を含む真空空間の静電感受率の 同じ体積の球形伝導体粒子を含む空間静電感受率に対する比である。




　図１の追加解説　
　F の εg 依存性を図１に示した。 a/b = ∞ は針状粒子、 a/b = 0 は円盤に対応する。通常の物質では εg < 4 なので、 粒子の形状が F に及ぼす影響は小さいことに注意せよ。また一方、軸比 a/b が 1 に 近い場合、 εg を無限大（伝導体）にしても伝導球とほぼ同じ 結果（何言ってんだか）を与える。

　平面波の減衰　
　角振動数 ω の平面波が空間電気感受率 χ(ω) = χ′(ω) - i χ″(ω) の媒質中を進んでいると想像しよう。減衰距離 L は次の式で与えられる。

　　　　　4πχ″ = (λ/2π)/L

波の減衰は吸収と散乱の双方で起きる。両者を含んだ減光断面積 σt を使うと上式は次のようになる。

　　　　　4πχ″ = N(λ/2π)σt

以上から静誘電率と積分減光断面積の間の関係が導き出せる。


　２．星間減光　

K-K 関係式を星間減光の式に　
　前章の L を Aλ=kpcあたりの減光(mag) に直し、λ を cm で表すと、

　　　　　4πχ″ = 3 × 10-22(λ/2π) Aλ

となる。便利のため、角振動数 ω を波長(μm) の逆数を u で表すと K-K 関係に現れた積分は以下のように変形される。

2 ∫ χ″(ω)dω = 3×10-26 Av ∫( Aλ ) du
π ω 4π3 Av u2


ここで、 Av は u = 1.82 の時の値である。 　一方、χ′(0) = Nab2F(a/b,εg) であった から、既知減光曲線の範囲が [u1, u2] の場合には、

Nab2F(a/b,εg) > 3×10-26 Av ∫ u2 ( Aλ ) du
4π3 u1 Av u2


空間中でグレイン体積が占める割合　
　さて、(4π/3)Nab2 = δ は固体物質が空間内で占める割合である。 従って、上式は次のようになる。

δ > 10-27 Av ∫ u2 ( Aλ ) du
F(a/b,εg) u1 Av u2


減光曲線　Aλ/Av　
　Aλ/Av は決して普遍的ではないが、とりあえず Whitford 1958 の表式を用いる。それは、

Aλ/Av = { 0.72u - 0.32 (0.44 < u < 2.3)
0.42u + 0.37 (2.3 < u < 3.0)
グレインの空間占有率　
この式を積分の中に代入すると、
∫ 3.0 Aλ du = 0.75
0.44 Av u2


となるので、

δ > 0.75×10-27Av du
F(a/b,εg)


　εg には赤外屈折率の二乗を使うべきである。積分が可視域に 限定されている現状では、より低振動数の積分の寄与もゼロ振動数誘電率に寄与している ことを考慮すべきである。つまり、　εg は大体 2 か、それよりうんと 大きくはない。図１に戻ると、 非金属のグレインでは　F は 0.3 程度である。したがって、 上の制限は、

　　　　　δ > 2.5 × 10-27 Av

Av = 1 mag/kpc とすると、固体物質の下限値は 10-27 gm cm-3 または 1 mag 当たりのコラム密度では 7.5 × 10-6 gm cm-3 である。この結果はグレインの大きさに関係しない。グレインの形には少し依存する。 もし、積分範囲が十分広く選べれば、不等号は等号になる。

　分子吸収　
　Platt 1956 は星間減光が分子または分子複合体により起こる可能性を調べた。しかし、 分子であろうと、εg = ∞ の制限を越すことはできない。なぜなら 越すということは分子の分極率が金属を上回ることだが、金属粒子は内部の電場をゼロに シールドするので、それ以上の分極はあり得ない。


　３．グレイン温度