アブストラクトIRAS PSC 中に低質量 YSO を探した。3種類の統計的方法を 69,436/245,889 天体に試した。分類法の性能は失敗アラームと 成功率で測った。Beichman et al 1986, Myers et al 1987 の YSO サンプルを結合したものに対する赤外の性質への近親度が二つの単純な 分類法では YSO 候補天体のランク分けされたリストに使われた。 第3の手法では赤外の性質と天空上の集合度とから2段階の分類法が 適用された。この結合は YSO と他種天体との分離を著しく改善し、 5825 個の YSO 候補を摘出できた。性能評価では その 87 % = 5068 個は本当に YSO であろう。カメレオン座 I 星形成領域でのサンプルを調べて それが真である事を確認した。それから推定すると最初のサンプルには 5962 個の YSO が混雑領域の外にあると思われる。この分類の質は カメレオン I 星形成領域内の最初のサンプルから IRAS PSC を調べる ことで実証された。 |
1.イントロ低質量だが近距離の YSOIRAS PSC で最も明るい天体は形成過程の大質量星である。しかし、より 低質量だが近距離の YSO もカタログに載っている。Harris et al 1988 は 既知の T Tau 星を IRAS PSC で調べた。しかし、より若い時期で埋もれた 天体については、 IRAS が最初の検出となる場合が多い。 Beichman et al. 1986, Clark 1987 は分子ガスを星形成域内の若い天体の指標に用いた。 多色データを使いきる PSC の分類は二色図に基づいて行われてきた。問題は、多色測光データの 内二色の分しか使われていないことである。そこで、最尤法を使用して データの情報を使いきることを目指す。さらに、それをタイプにより異なる 集合性の性質と結び付ける。しかし、これは銀河面のように混んだ所や、 LMC のように原因が違うところでは効き目が悪い。そこで、銀河面 から外れた所に限定してこの手法を適用する。 |

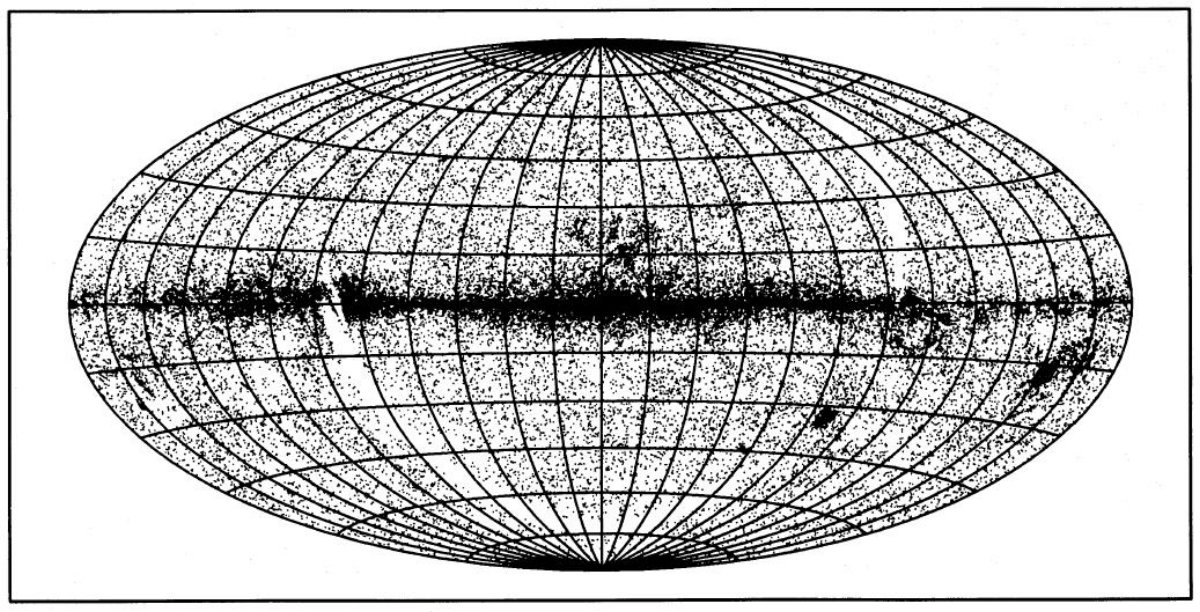
2.イニシャルサンプル(1)IQ(60, 25) = 2, 3 で log (F12/F25) < 0.05(2)log(F25/F60) < 0.25 こうして 69,436/245,889 天体が選ばれた。これをイニシャルサンプルと 呼ぶ。図1にその分布を示す。 3.分類法の性能Beichman-Myers サンプルとヒット率Beichman et al 1986 と Myers et al 1987 は低質量星形成領域の IRAS 天体 58 個を選び出した。 Emerson 1987 はそれらが深く埋もれた 原始星から T Tau までの広い範囲の進化段階にあることを明らかにし、 それらを コア天体と T Tau 天体に分けた。 |
この論文ではこれらの天体を Beichman-Myers サンプル と呼び、
分類法がこのサンプルをどの位含むかでヒット率を調べる。
高銀緯銀河と間違い率 |l| > 50°: の イニシャルサンプルはほぼ確実に銀河である。 そこで、それらは全て銀河と仮定し、分類法がどのくらいそれらを含 むかで間違い率とする。 |
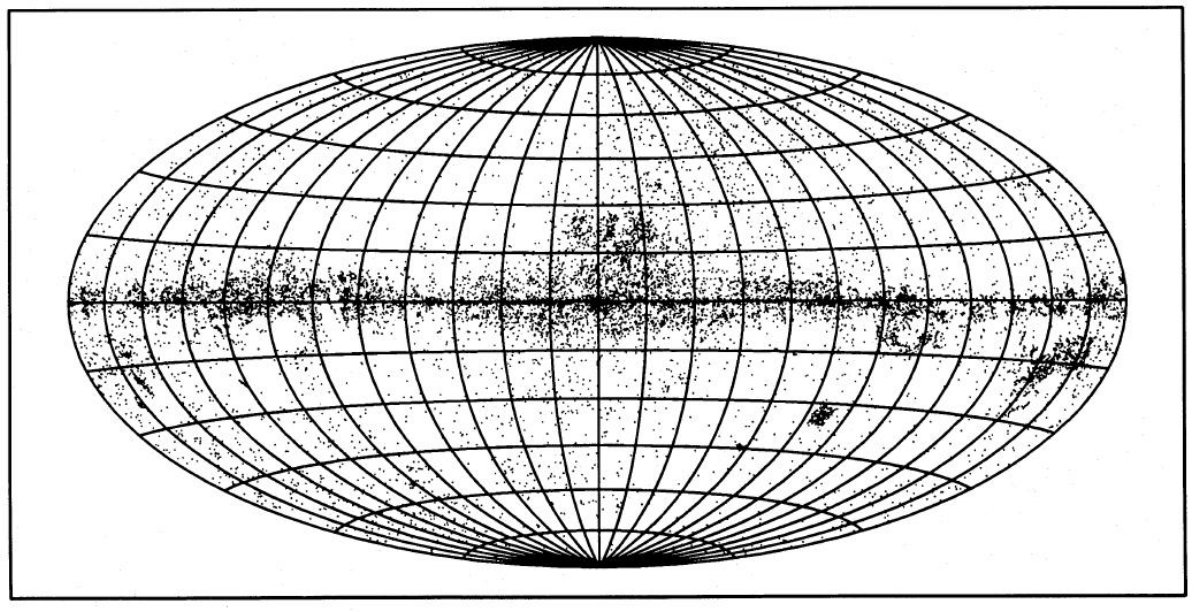
4.1.分類法13次元ガウシャンでフィットX = log(F12/F25), Y = log(F25/F60), Z = log(F60/F100) 空間で Beichman-Myers サンプル分布を3次元ガウシャンでフィットする。 この分布関数を使って、イニシャルサンプルの各点に対して分布確率 を計算する。そしてそれら B-M サンプルを rank-order する。 境界値の設定 問題はこうして確率の高い順に並べら直されたイニシャルサンプル のどこに "operating point" = 操作点を設定するかである。 幾つかの設定法が考えられる: (i) 確率の大きい順で N 個を選ぶ。 (ii)間違い率の許容値を決める。 (iii)ヒット率の要求値を決める。 (iv)最大尤度を用いる。 最後の3つの方法は O-C 図2で示される。(ii) と (III) は図2の 曲線 a に対して垂直(ii)、水平(iii) 直線を引く事に対応する。 (iV) は曲線の傾きが 1 となる点、つまり間違い率とヒット率が同じ 速さで増加する所を境界値と決める。 分類法1の特徴 分類法1の特徴は曲線 a に見られるように殆どの箇所で傾きが 1 で ある。このため、方法 (iv) をどこで採用すべきかを決めにくい。 図3にはヒット率 50 % とした時の 16750 天体天空分布を示した。 この場合の間違い率は 21 % である。 |
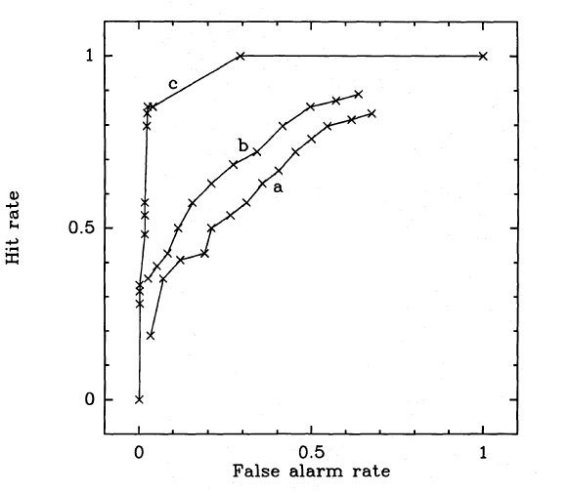 図2.3 種類の分類法の動作の特徴。 曲線a. 分類法1。カラー空間の分布確率(ガウシャン)の高い順。 曲線b. 分類法2。1に 100 μm を加えた。 曲線c. 分類法3。カラーと F100 で銀河、厚い円盤、薄い円盤に分け、 次に円盤天体を集合度で選択する。 |
4.2.分類法2固有光度とフラックス区分分類法1に F100 を付け加えると、サンプル内で距離に大きな分散 があっても、タイプ間で光度に大きな差がある場合には分離に有効な のである。一般に銀河面すれすれに見つかる銀河系天体は、銀河面から 離れても見つかる天体より明るい。勿論、ある種に固有な光度があっても 距離の広がりによりその違いは均されるのだが。銀河は一般には銀河 面すれすれ天体より低いフラックスを持つ。 分類法2による結果 図2の曲線 b はこの様な分類法2による結果である。図から判るよ うに、分類法2は分類法1に較べると進歩がある。ヒット率 50 % の ラインでの間違い率は 21 % から 12 % へと低下した。 |
log F100 導入の効果 B-M サンプルは距離 140 - 900 pc, 光度 0.3 - 230 Lo に広がる。 その結果は F100 = 4 - 820 Jy となった。このフラックス分布を 分類法2に組み込んだ。図2の曲線 a から曲線 b への改善がその 効果を示している。 スペクトルの類似性に依存する分類法1、2は一つの二色図だけで行 う分類法の拡張であり、改善が見られたが決定的ではない。これは Emerson 1987 が行った B-M サンプルの解析から明らかである。彼はコア天体から T Tau 型星に至るサンプルの性質を調べ、これらが特定のカラー領域 から選ばれたのはあるが他のタイプの天体に較べずっと広い領域を カバーすることを示した。特に、赤外カラーが銀河と大きく重なって いることは重要で、他の情報を導入して分類精度を上げる必要がある。 |
4.3.分類法3戦略この方法は最初に銀河を銀河系天体と分離し、次に銀河系天体を 集合度で分類する。B-M サンプルは分類の調整に使用される。5.3節 でカメレオン星形成領域を使ってこの手法の有効性を確かめる。 トレイニングセット Adorf,Meurs 1988, Meurs et al 1988, 1989 で述べたやり方に従い、 3種類のトレイニングセットを使って最大尤度分類を訓練する。それらは、 銀河、薄い銀河面、厚い銀河面の3つである。厚い銀河面種族は以前の 文献ではシラスと呼ばれていた。銀河トレイニングセットはイニシャル サンプルから選ばれた |b| > 50° の 5774 天体から成る。 薄い銀河面セットはイニシャルサンプルから、 |b| < 1°, -50° < l < +40° の四角領域の 6737 天体が取り上 げられた。このサンプルは主に埋もれた若い HIIR で占められている。 厚い銀河面セットは Ophiuchus-Scorpius の四角形 -15° < l < +5°, +10° < b < +25° 内の 1132 天体である。これらは主に YSO、反射星雲、 進化星、PN と考えられている。イニシャルサンプルをこれら3カテ ゴリーに分割することが正しいことは図4が示している。 混入 薄い銀河面成分と厚い銀河面成分への銀河の混入は銀河の密度が全天で 一様という仮定で夫々 2 %, 15 % と評価された。しかし、IRAS PSC では 銀河密度が低くなるので、この値は過大であろう。 トレイニングセットのデータ分布関数 IRAS カラー log(F12/F25), log(F25/F60), log(F60/F100), と フラックス log(F100) の分布を各トレイニングセット毎に4次元ガウ シャンでフィットする。 カテゴリーへの帰属の決定 すると、イニシャルサンプルの各天体毎に、3つのカテゴリーに属 したとしてそのカラーとフラックスである条件付き確率が計算される。 天体の帰属カテゴリーはこの条件付き確率が最も高い ところと決められる。こうして 69,436 天体は、銀河 16,524, 薄い銀河面 21,968, 厚い銀河面 30,944 天体へと分けられた。B-M サンプルは厚い 銀河面種族か薄い銀河面種族へと分けられ、銀河に行った天体はゼロで あった。 |
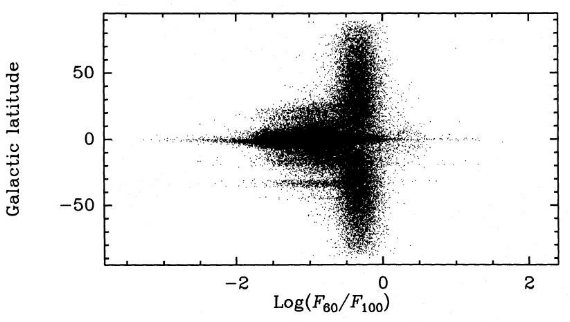 図4.イニシャルサンプル 69,436 天体の log(F60/F100) 対 b 分布。 銀河は -0.7 < log(F60/F100) < 0 で一様な分布を示し、低銀緯 になると個数密度が低下する。イニシャルサンプルの第2成分は、 log(F60/F100) が広い範囲に分布し、銀河面に著しい集中を示す。第3 成分もまた銀河面に集中するが銀緯分布はより幅広で、 log(F60/F100) 分布はより狭い。 集合性= YSO の選別 二つの銀河系天体グループから YSO 候補を選び出すために集合性を 利用する。これは Clark 1987 がアンモニアコアの周囲で天体密度が急増 することを発見したことから考え出された方法である。天体を中心とする 円内の星密度から、周囲円環のフィールド密度を引いて密度超過を測る。 集合性の天体の分別には単純な κ-σ 飛び跳ね者検出法が 用いられる。 x = 密度超過の境界値 m = 平均数密度 σ = B-M サンプルに対する超過密度の標準偏差 境界値 x は次の式で κ へとパラメター化される。 x = m + κσ 試行の結果、半径を 8', 16', 32' として、そのどれかで密度超過が 境界値を越えれば YSO に分類する方法が最良の結果を産み出した。 その結果が図2の曲線 c である。 (曲線を作るにはxを変えていくのか?) 最終候補 この分類法の操作点は前と同様傾き=1で決められる。それは κ = 0 となる点を決める。これは YSO 候補 25,986 天体を選び出した。 図5はそれらの分布図である。ヒット率 = 85 %, 間違い率 = 2.6 % です。 25,986 天体はしかし、混雑がひどい領域を含む。そこで、混雑度の薄い 領域に限定すると 5825 天体が残った。 |
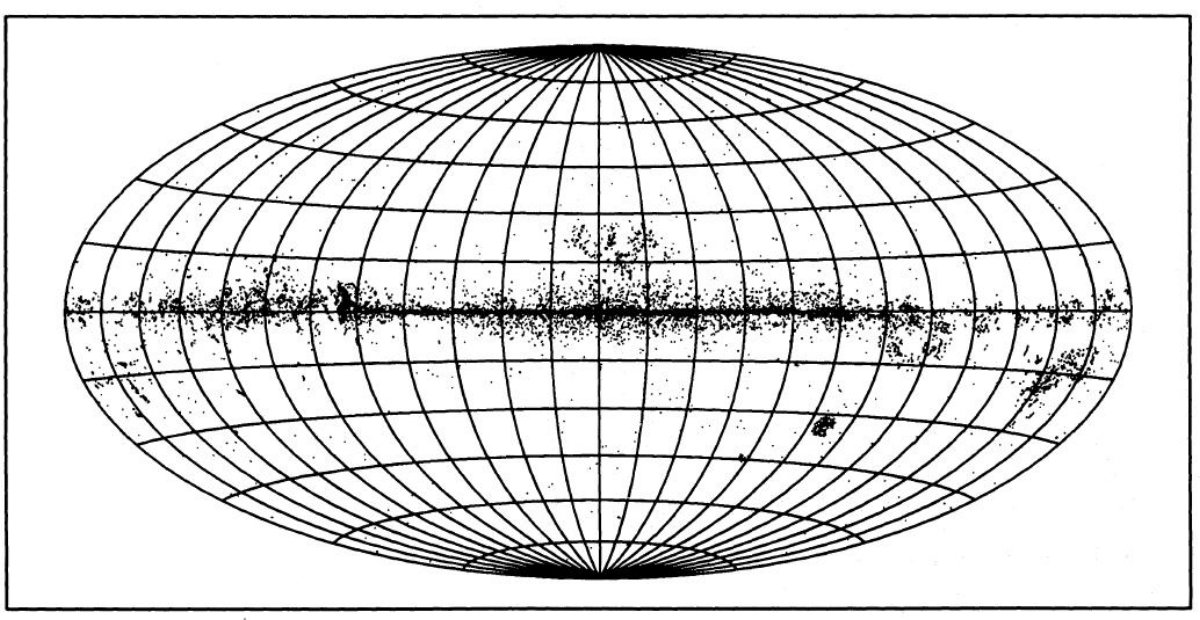
5.1.集合バイアスマゼラン雲と銀河面表1にはいくつかの有名な天域における候補天体の分類を示す。 マゼラン雲では IRAS 点光源は実は YSO とダスト雲の塊りであり、 空間分解能が低いため単一天体に見えたのである。これらは我々の 考える低質量天体ではない。 銀河面も注意が必要な領域である。そこでは視線方向が 偶然重なった天体が集合のように見えてしまう。 太陽近傍の星形成領域 この二領域を外すと残るのは太陽近傍の星形成領域に属する 5825 天体である。 5.2.サンプルの質6.結論 |
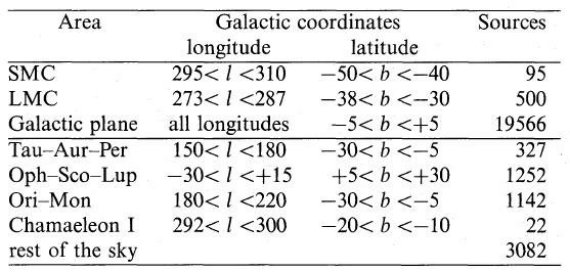 表1.25,986 天体の区別。 |