| 種族 I と II の矮星と巨星に合った、 Teff, log g, 組成のグリッド上で MARCOS プログラムを用いてモデル大気を計算し、SSG コードで人工スペクトル を導出、ワシントンシステムでの指数を計算した。 C, N 量が巨星 カラーに及ぼす影響も求めた。モデルカラーを文献から集めた観測値と比較した。 我々の矮星モデルは観測された円盤矮星系列とよく合う事が判った。一方、 太陽組成巨星モデルは観測円盤巨星系列と合う。しかし、低メタル等時線は 球状星団巨星枝に比べると系統的に赤過ぎた。これは計算のパラメターのため かも知れない。 | T1-T2 と M-T2) から有効温度を 推定する際の組成と重力による影響を比べた結果、後者の方がより良いことが 判った。(C-M) も (M-T2) も [C/Fe] や [N/Fe] の変化に対し とくに敏感ではない。しかし、太陽組成では (C-M), (M-T1), (T1-T2) は組成が反相関していないと強い影響を受ける。 (C-M) と (C-T1) が組成指数として最もよいという経験則を 計算で確かめた。重力の指標としての (M-51) 指数は観測系列とよく合った。 この指数は重力と組成の双方に有用である。特に非常に赤化の大きな散開星団、 球状星団の組成を決めるのに有用であろう。 |
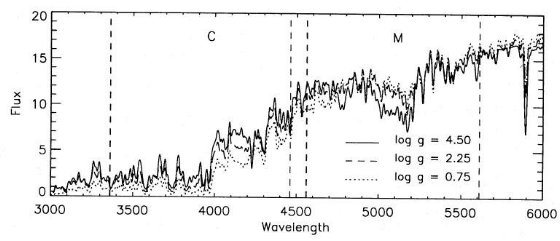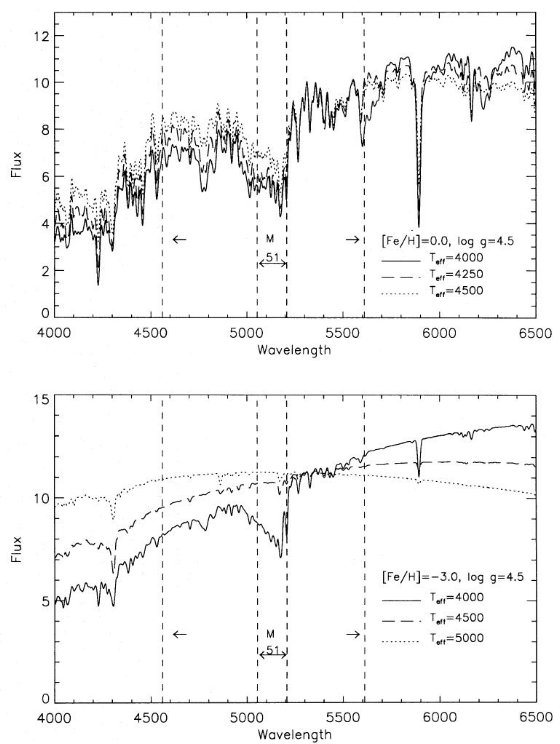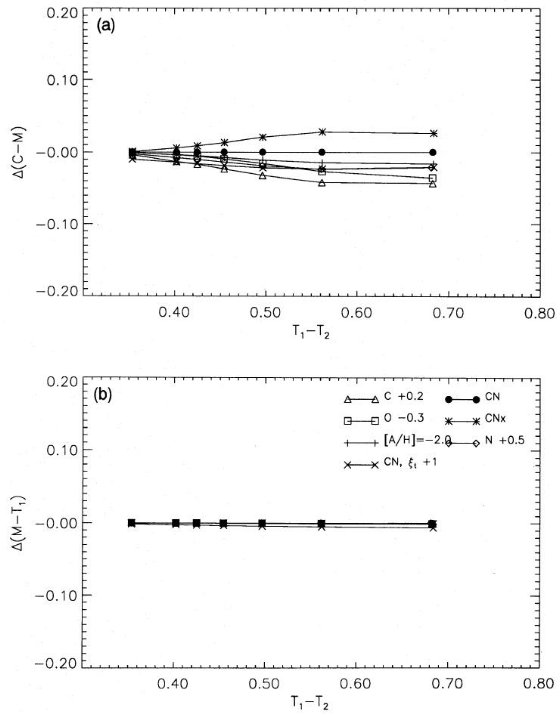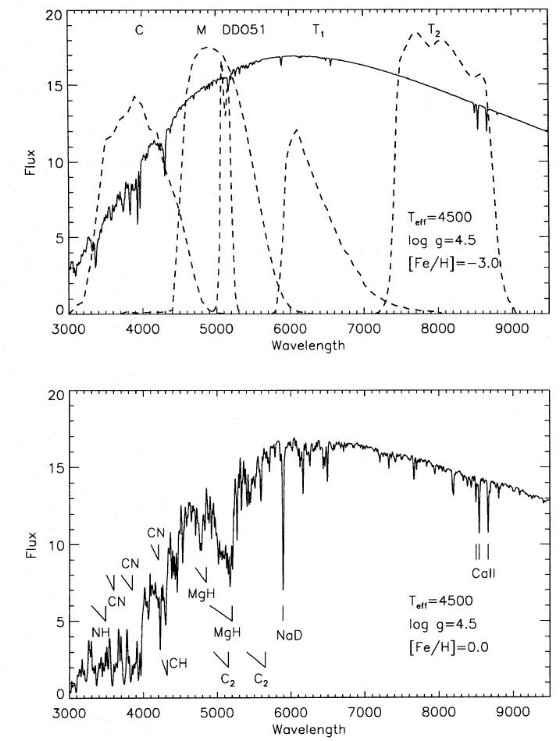
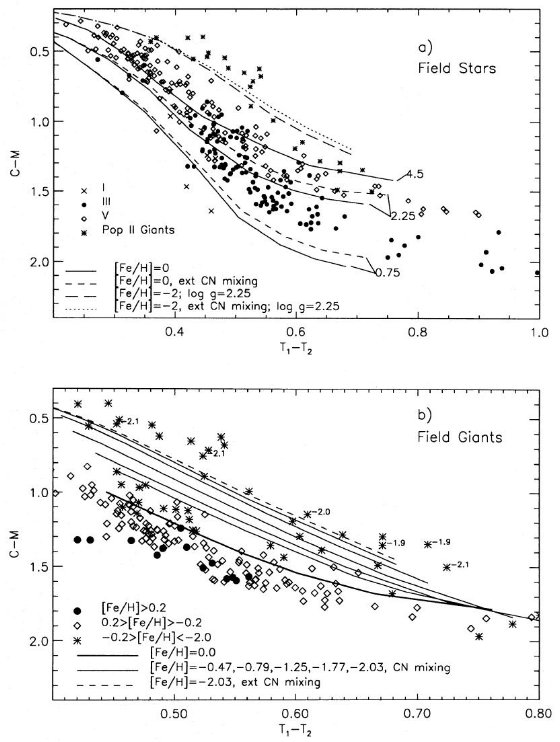
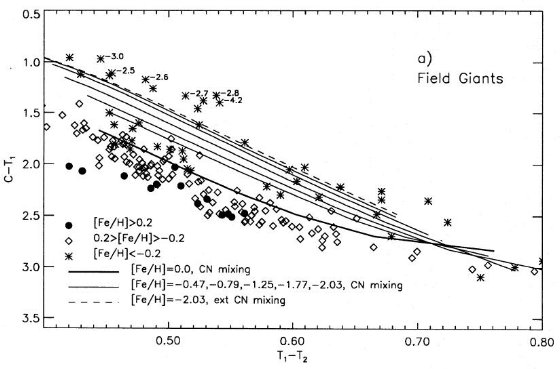
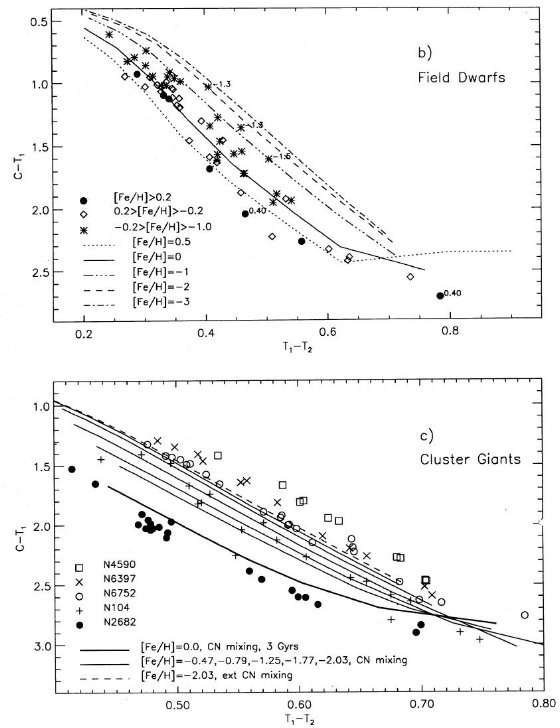
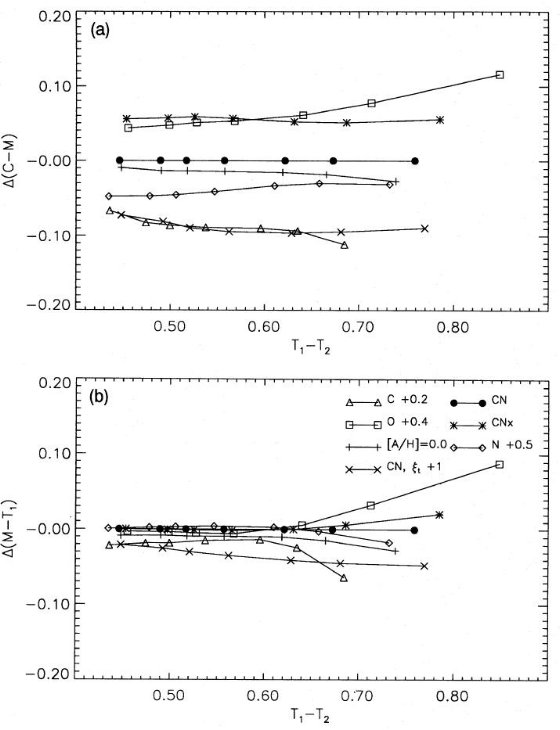
 図１．（上）拡張ワシントンシステムのパスバンド。 4500K [Fe/H]=-3.0 矮星 スペクトルを重ねた。（下）4500K, [Fe/H]=0 矮星スペクトルの吸収帯。  図３．(C-M) 対 (T1-T2) 二色図。 (a) 矮星と巨星。log g = 4.5, 2.25, 0.75 モデルを CN ミックシングがありと なしの場合につき示す。以降、 "ext CN mixing" は [C/Fe]=-0.7, [N/Fe]=+0.7 を 指し、"CN mixing" は [C/Fe]=-0.2, [N/Fe]=+0.4 を指す。 (b) フィールド巨星。等時線と比べた。 |
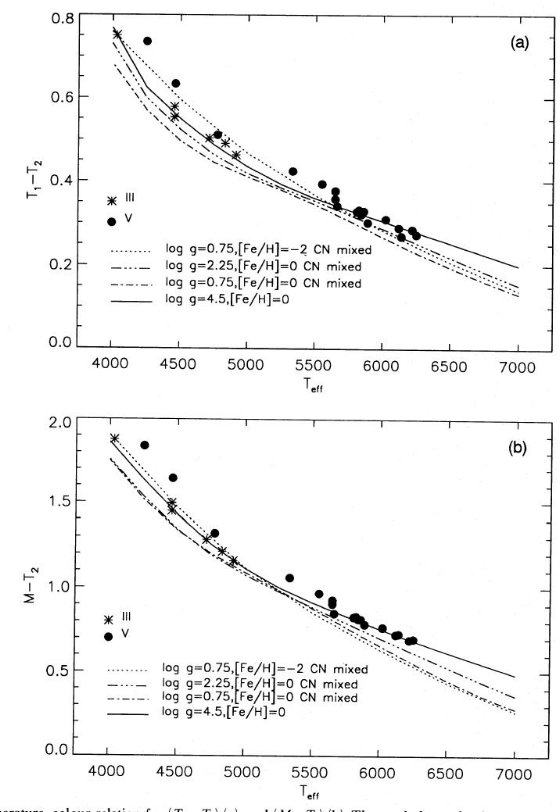
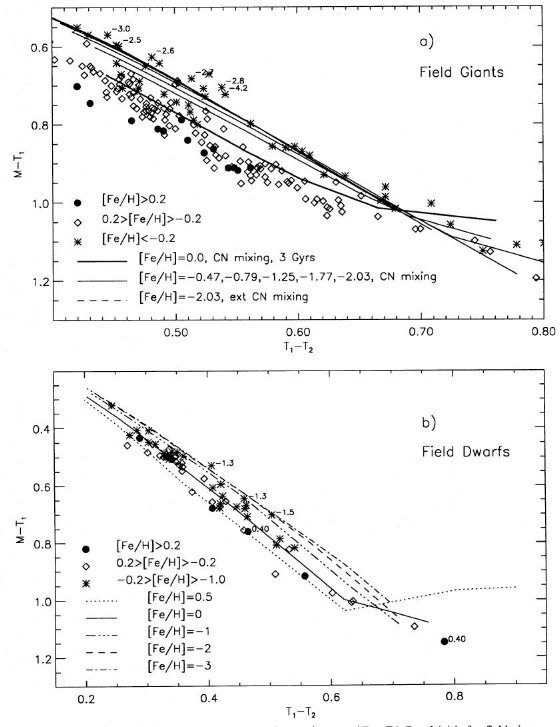
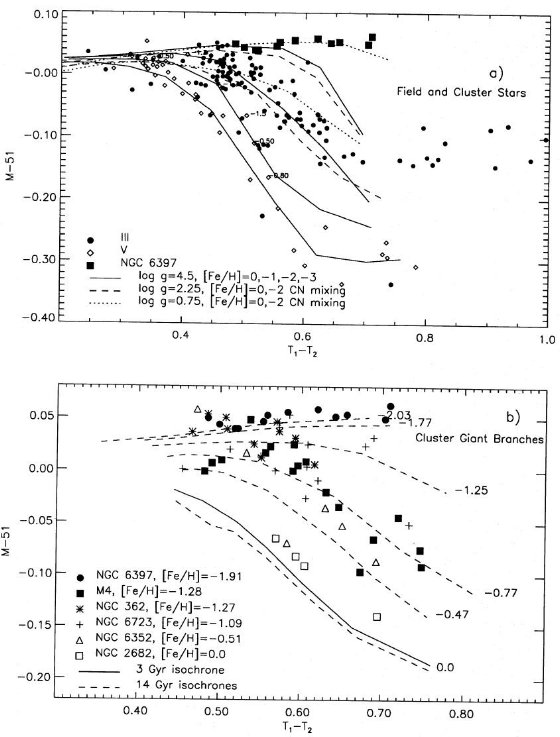
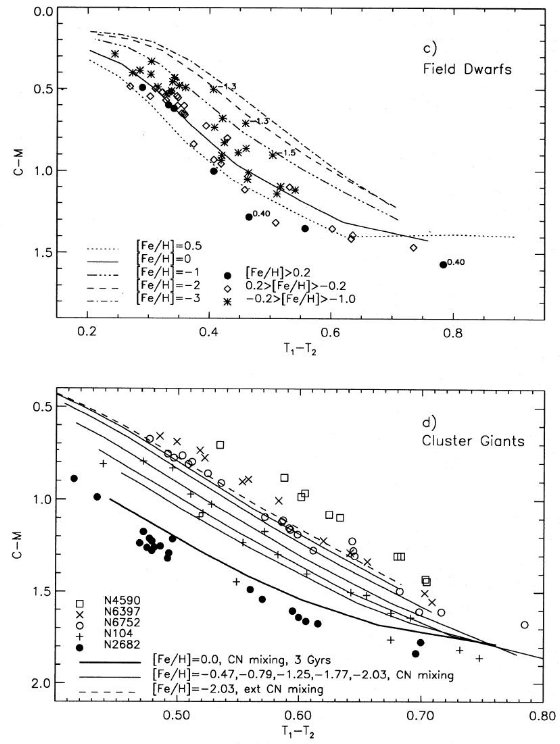
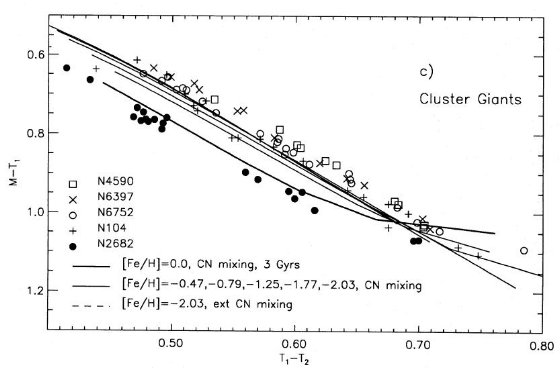
 図２．有効温度と二つのカラーの関係。黒丸=矮星。星＝巨星。  図３続き。(c) フィールド矮星。（ｄ）星団巨星枝星。 |
| 図４．C, M パスバンドでの重力の影響。温度 4500K, で重力が３通りの スペクトルを示す。log g が下がるに連れ、 C, N 分子吸収が強くなり、 一方 4800 A, 5100 A の MgH バンドが強まる。 |
 |
 |
 図５続き 図５．(M-T1) 対 (T1-T2) 二色図。 (a) フィールド巨星 (b) フィールド矮星 (c) 星団巨星 |
 図６.(C-T1) 対 (T1-T2) 二色図。 (C-T1) の性質は (C-M) と似ている。 (a) フィールド巨星 (b) フィールド矮星 (c) 星団巨星 |
 |
 図７．(M-51) 対 (T1-T2) 二色図。 （上）フィールド星。様々なメタル量に対して、重力一定モデル線を示す。 太陽組成の場合、矮星と巨星の観測点ははっきりした２系列に分かれる。 （下）星団の巨星枝星。一般に等時線と良い一致を示す。 |
 図８．MgH バンド強度に及ぼす温度と組成の影響。 （上）高メタル。温度が下がると 5100A の Δv=0 系列が強まり、 Teff < 4250 K では飽和する。 （下）低メタル。MgH は弱いままで 4500 K 以下でやっと強まる。 |
 図９．ＣＮＯ量とマイクロ乱流の効果 |
 図１０．同じ |