Effective-Medium Theories for Cosmic Dust Grains

　アブストラクト　

　１．イントロダクション　

　２．有効媒質理論　

　２．１．レイリー近似における T-マトリックス法 = TMM　

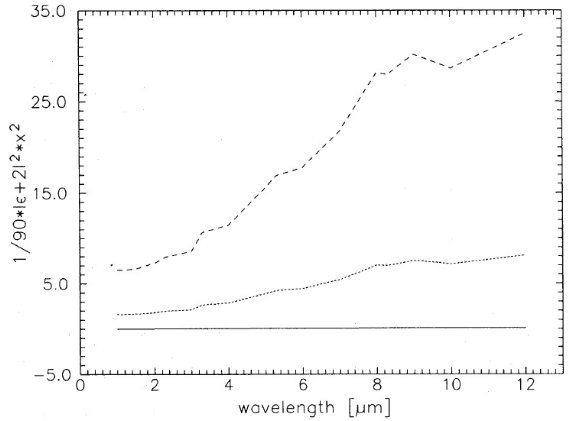
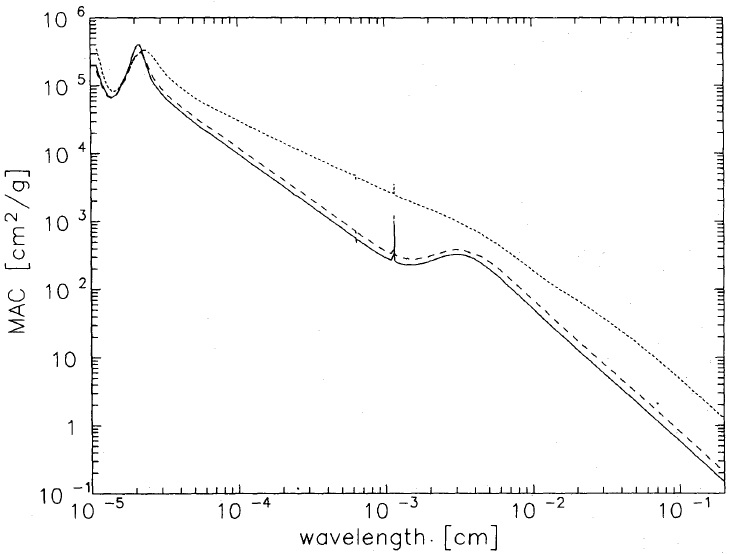
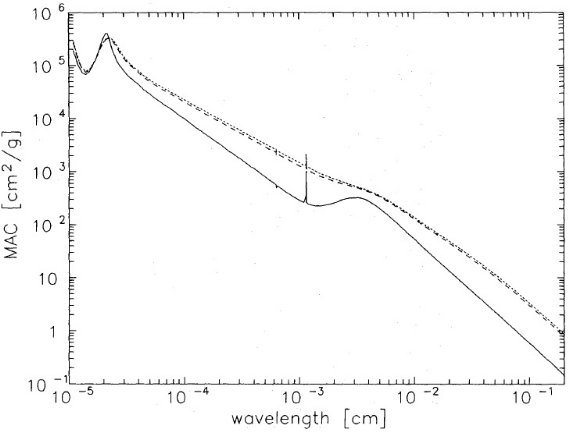
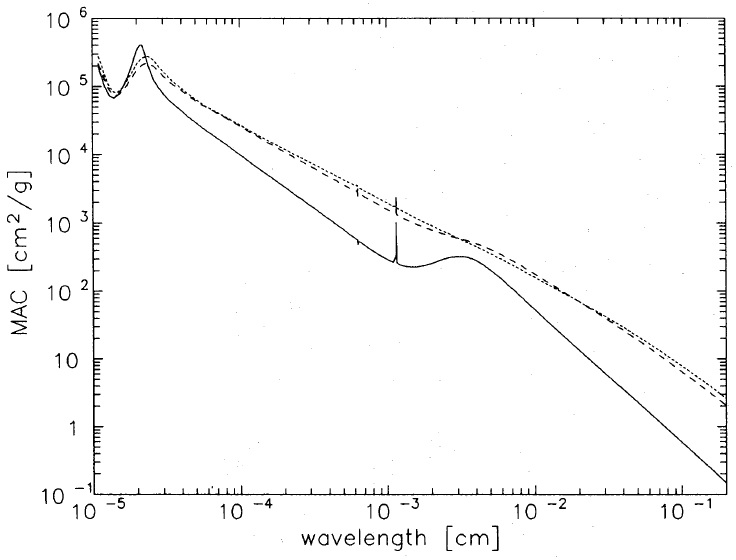
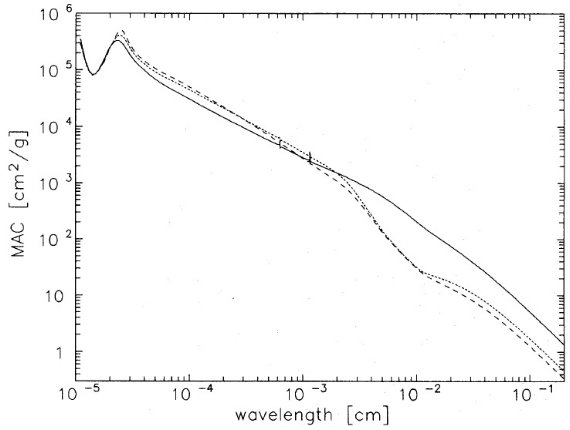
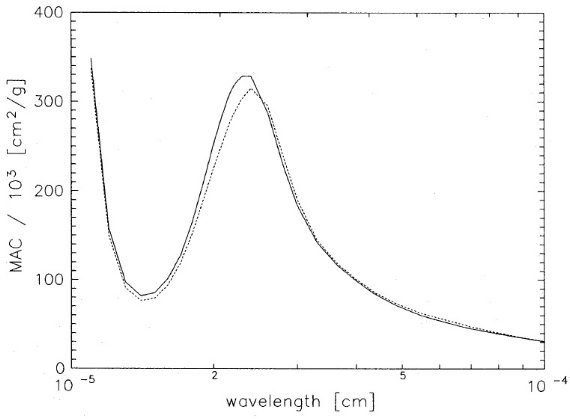
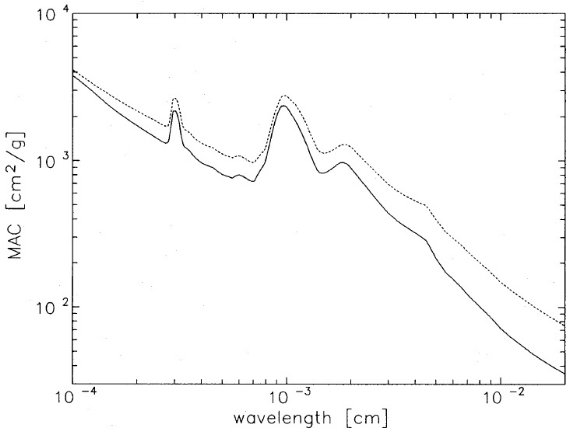
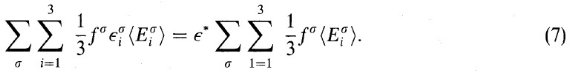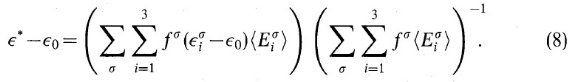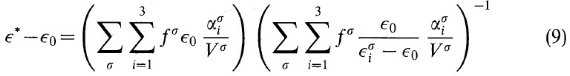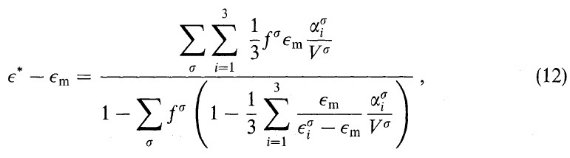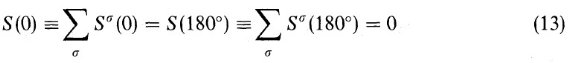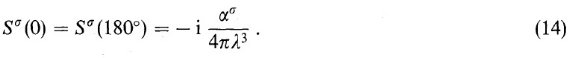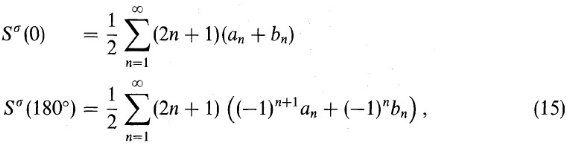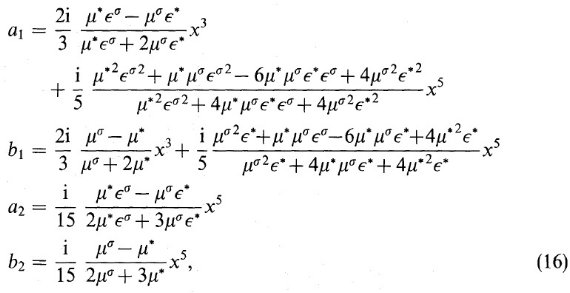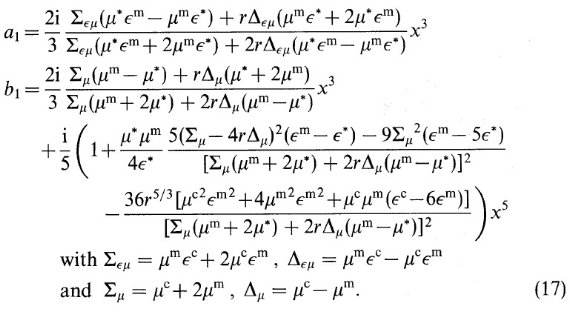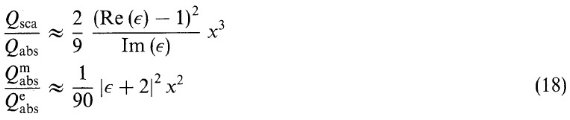有効誘電関数 ε* 　 　TMM では、有効誘電関数 ε* は次の式に従う。 ここで、角括弧は非一様グレイン全体にわたっての平均値を表す。レイリー近似 は、準静電気学の関係が適用される、つまりセルの大きさが波長より小さいことが 条件である。TMM では非一様物質の全ての粒子以下の区画は双極子で表される。 この双極子は粒子サイズ以下の区画が周囲環境に対して持つ分極率で特性付けられる。 この方法では、分極率の代わりに T-行列を使う。双極子間の作用は直接扱わずに、 全てのグレインの環境に対して適切な誘電関数を選ぶことで考慮する。 　マクスウェル・ガーネット と ブラッジマン 　 　マクスウェル・ガーネット 法では、非一様物質は基質内に別種の含有物が低 密度で埋め込まれていると仮定する。基質物質の誘電関数 εm = εm (セル周囲の背景)と看做す。ブラッジマン法では構成物質の どれも支配的でない。自己無矛盾な周囲背景誘電関数が有効誘電関数として求まる。 すなわち εm = ε0 である。 　　 　個々のセルの分極率は、次の式で決まる。 ここに、ασi = セル σ の i- 方向の 分極率。ε = セル σ の i- 方向の誘電関数。楕円体は EMT に 扱いやすい。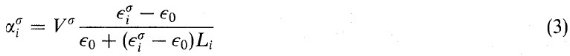その種軸方向の分極率は、 ここに、 Li = 0 と 1 の間の幾何学ファクターで、球の場合には、 L1 = L2 = L3 = 1/3、円盤では L1 = 1, L2 = L3 = 0, 棒では L1 = L2 = 1/2, L3 = 0 である。

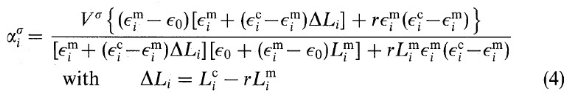
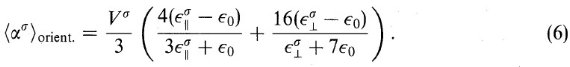
コア-マントルの分極率　 　同じように、楕円体形のコア-マントルグレインの分極率は、 ここに、εci = コアの誘電率、 εmi = マントルの誘電率、 Lci = コアの反分極ファクター、 Lmi = マントルの反分極ファクター、r = コアの体積比である。 　方向平均　 　非一様グレインの性質を求めるには、サブグレイン σ の電場方向に 対する向きを平均する必要がある。特にどの方向も優先されないとすると、 　例として、グラファイトグレインを直径/厚み = 5 の楕円体と仮定すると、 大体、L1 = L2 = 1/8, L3 = 3/4 である。 平均分極率は、 ここに、ε⊥ = 電場がグラファイト膜の法線に直交する 時の誘電関数、ε|| = 電場がグラファイト膜の法線平行な 時の誘電関数である。 　他の形状　 　他の形状に関しても計算可能だが、時間が掛かる。

アンサンブル平均　 　アンサンブル平均には、グレインに含まれる全ての種類のセル σ とその 向き全体が含まれる。特に楕円体の場合は３本の主軸の方向を考える。すると、 ここに、fσ = σ 種セルの体積比。i = 幾何学的方向。 上式を書き直して、 式 (2) と合わせると、有効誘電関数を分極率に基づき、下のように得る。

ブルジマンの仮定　 　ブルジマンの仮定では &eppsilon;0 = &eppsilon;* なので、 式 (3), (4) からの分極率と一緒に、この式は任意の、等方または非 等方の誘電関数を有する非一様な媒質の一般化されたブルジマンの式を与える。 　マントルなし、裸で、球形の等方的誘電関数の場合には、良く知られたブルジマンの 式になる。 　マクスウェル・ガーネットの仮定　 　マクスウェル・ガーネットの仮定では &eppsilon;0 = &eppsilon;m なので、式 (9) の分子で、基質媒質からの寄与はゼロで、分母への 寄与は 1 である。こうして式 (9) は次の式 (12) と書換えられる。 ここに、和は含有物 σ だけで取り、基質は含まない。この式は一般化した マクスウェル・ガーネットの式と看做せる。含有物質が等方的で球形の場合は伝統的な マクスウェル・ガーネットの式に戻る

　２．２．散乱行列法 = SMM　

SMM = scattering matrix method とは　 　有効媒質法のもう一つの方法は散乱行列法 SMM = scattering matrix method で、 Chylek, Srivastava 1983 が提案した。 Bohren 1986 が批判したように、彼らは透磁率を考慮しなかったが、彼らの方法は 混成媒質における磁気双極子の効果を考える途を開いた。EMT と同様に SMM も 混成媒質内のサブグレインは波長より短い場合しか扱わない。SMM ではサブグレイン はミー理論で決まる散乱式で扱われる。粒子の集合が仮想的な有効媒質に埋め 込まれると、それらは透明になるというのが散乱行列法の考えである。それを 数学的に表現すると、 　レイリー粒子の場合　 　レイリー粒子の場合、振幅と分極率の間に次の関係が成立する。 式 (13) と (14) から、　TMM と同様に式 (10) が導かれる。 　球粒子　 　球粒子では散乱振幅は次の式で与えられる。 ここに、an, bn は n-次の散乱係数である。係数の導出は、 Bohren, Huffman 1983 にある。

サイズパラメタ― x = 2πa/λ を使うと、 ここに、ε = 誘電関数、μ = 透磁率。σ と * はサブグレイン種、 周囲環境をそれぞれ表す。με = μ* の場合には上式は通常のミーの散乱項になる。 　コア・マントルグレイン　 　コア・マントル球形グレインには類似するが、少し複雑な式が成立する。興味 のある最初の３項は、 ここに、c はコア、m はマントルを表す。マントルが 基質物質、コアが含有物と看做すと、式 (13), (15), (17) を合わせて、複合媒質 のマクスウェル・ガーネット式を磁気双極子項を含んで表現できる。 　ε* と μ* の決定　 　ε* と μ* の決定は式 (13) から行われる。 これには様々な数値法が存在する。課題の一つは、最も有意味なルートの選択である。 これまでのところ、計算された関数は単に数学的に式 (9) または (13) を満たすに過ぎない。 体積比が大きい物質がある場合、複合体の光学定数はその物質の値に近く成らなくては いけない。比較的簡単な数値的基準として、定数には加算平均を取った解を選ぶ。これは、 複合媒質が材料媒質に親近することを保証する。

　２．３． EMT の限界　

多重散乱理論　 　EMT の計算では、近似の限界に注意しなければならない。Varadan et al 1973 は、サブグレイン間の散乱が生じ、含有物の体積比が 1 % くらになったら、 る場合、EMT の代わりに多重散乱理論を用いなければいけないことを証明した。 これはサブグレインの体積に関する強い制限である。 　TMM と SMM との比較　 　TMM と SMM とを比較すると、 TMM は形状の扱いでより一般的である。なぜなら、 セルの電気双極子だけが計算可能だからである。一方、 SMM では散乱式が少なく とも誘導磁気項が現れるまでは既知の必要がある。ただ、磁気効果は SMM でのみ 考慮されている。両手法の結合は可能で、魅力的である。 　EMT はグレインの吸収が強くなると良い近似　 　EMT が適用可能かどうかの基準は この表式を相対誤差と較べる。一般に、 EMT はグレインの吸収が強くなると良い近似 になる。 　チェイン　 　何を書いているのか分からない。 　ここで扱う形状　 　ここでは体積率が 10 - 50 % の球状サブグレインが媒質内にある場合を扱う。 有効形状は、球、無限長の棒、無限大平面である。 図１a には、 Draine, Lee (1984) の天文シリケイト、 a = 10 nm の吸収効率を示す。空隙率を 40 % とした。図１b にはモデル間の相対誤差を示す。

図１．空隙部 40 % の空孔質シリケイトグレイン。半径 10 nm. (a). 実線＝ DDA 計算。点線＝古典的ブルジマンモデル。破線＝有効形状のブルジマンモデル。 (b). 実線＝古典的ブルジマンと DDA モデルの相対差。点線＝有効形状ブルジ マンと DDA モデルの相対差。

　３．応用　

　３．１．ダーティシリケイトと磁気双極子　

鉄含有物の影響　 　Ossenkopf, Henning 1990 は基質を様々な実験室シリケイトの混合物とし、 含有物は鉄の微粒子とする。鉄の半径は 7 nm, 60 nm, 120 nm とし、体積含有 率＝ 5 % とする。SMM のマクスウェル・ガーネット近似を適用する。図２a と 図２b は、誘電関数と相対帯磁率スペクトルを示す。図２c は質量吸光率を示す。 図を見ると磁気双極子項は 7 nm の場合全く効いていない。有効透磁率は１である。 60 nm グレインではかなりのズレを生じさせ、 120 nm では全スペクトルで支配 的になる。 　　 　 図２．鉄粒子を含有するシリケイト。体積含有率＝ 5 %. 鉄粒子半径は, 実線＝ 7 nm. 点線＝ 60 nm. 破線＝ 120 nm. (a) 誘電関数。(b) 相対透磁率。(c) ３種混合の半径 200 nm グレインの質量吸光係数。 (なぜ誘電関数の絶対値なのか？ 鉄無しからどう変わったか分からない。)

磁気双極子　 　磁気双極子はどの波長でも吸収効率を上げる。増強率はシリケイトの吸収 極大の付近で最も大きい。 4 μm 付近ではズレは殆ど生じない。 誘電関数も相対透磁率も大きく変わるのだが、ε* と μ* とが互いに相殺しあうのである。 　鉄の磁気吸収　 　図３には、式 (18) の (1/90)|ε+2|2x2 を鉄粒子の相対磁気双極子吸収の目安として示す。グレインが大きいと、 磁気吸収が電気吸収を大幅に上回る。有効誘電関数への影響はそれほど大きく はない。それは含有比が小さいからである。 　これらの計算は実際上の妥当性は有しない。なぜなら、そんなに大量の鉄粒子 が拡散星間空間に存在することはあり得ないからである。 図３．磁気吸収と電気吸収の関係を式 (18) の (1/90)|ε+2|2 x2 で評価。鉄粒子の半径は、実線＝ 7 nm, 点線＝ 60 nm, 破線＝ 120 nm.

　３．２．フラクタルグレイン　

フワフワ粒子の吸光　 　合体で成長した星間グレインはフラクタル構造を有する。Henning et al 1989, Ossenkopf 1990 はフラクタル粒子が存在する観測上の証拠をレビューしている。 そのようなフワフワ粒子の光学的性質の計算は Mathis, Whiffen 1989 が行った。 彼らは単純ブルッジマン則を適用した。Hage, Greenberg 1990 はフラクタル性を 無視したフワフワ粒子の吸収を計算した。 　フラクタル構造　 　フラクタル構造では、大きい粒子ほど空隙率が大きく、中心部の密度は外層 より大きい。複合粒子の密度は大きさと次の関係がある。 ここに D = フラクタル次元。 D = 1.7 - 2.7 と推定される。

ふわふわ粒子の吸光は強い　 　図４にはグラファイトの MAC = mass absorption coefficient スペクトルを 示す。図から、間隙率が大きいと孤立粒子と同じ吸収を与えることが判る。当たり前 だが。しかし、中間間隙率では、MIR, FIR で吸収係数が最大 6 倍になる。220 nm のコブは幅が広がり、長波長側に移る。つまり、同じ質量でも、ふわふわ粒子は より多くの光を吸収する。DDA 計算も大体同じ結果を与える。 　半径分布の考慮　 　図５には孤立グラファイト粒子だが、半径分布 a-3.5 の合体 フラクタル粒子の MAC を半径上限 0.1 μm と 0.45 μm の場合で示す。 半径上限値は吸収に殆ど影響しないことが判る。大きなフラクタル粒子 は密度が低いため、サブグレインが孤立粒子のように働き、かつ大きな粒子 には質量がほとんどないためである。この理由で、 Mathis, Whiffen 1989 の計算では間隙率 0.8 でフラクタル性を無視したが、割と良い結果を得た。

図４．グラファイト粒子の質量吸収係数。実線＝半径 7 nm の分離タイプ。 点線＝空隙率 0.55 の半径 15 nm 合体グレイン。破線＝空隙率 0.95 の半径 270 nm 合体グレイン。

図５．グラファイト粒子の質量吸収係数。実線＝半径 7 nm の分離タイプ。 点線＝半径 7 - 100 nm で n(a) ∝ a-3.5 フラクタル次元 D = 11/6 の合体グレイン。破線＝半径 7 - 450 nm で n(a) ∝ a-3.5 フラクタル次元 D = 11/6 の合体グレイン。

図６．図５と同じ質量吸収係数だが、合体粒子のフラクタル次元 D = 5/2.

図７．合体グラファイトグレインの質量吸収係数 MAC. 間隙率＝0.55, a = 15 nm. サブグレインは、実線＝球。点線＝主軸/短軸が５の円盤。破線＝主軸/短軸が無限大 の円盤。

図８．複合グラファイト粒子の質量吸収係数。間隙率 = 0.55.　複合粒子半径 = 50 nm. サブ粒子半径は 実線＝ 7 nm, 点線＝ 20 nm.

図９．実線＝シリケイトコア＋アイスマントルグレイン、非晶質炭素グレイン、グラ ファイトグレインが分離状態で混合した場合の質量吸収効率。 点線＝上の３者が合体し、半径分布 n(a) ∝ a-3.5 を持った場合の 質量吸収効率。 (混合比率が分からない。 )