|
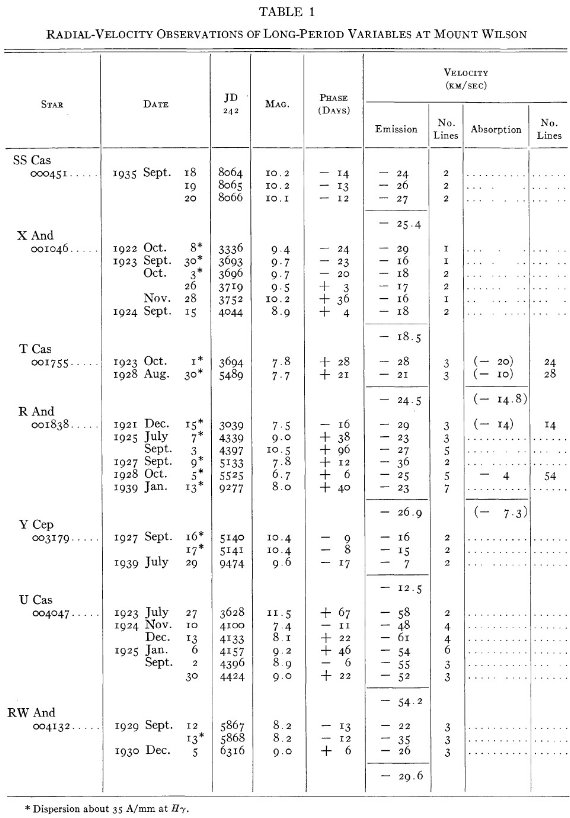
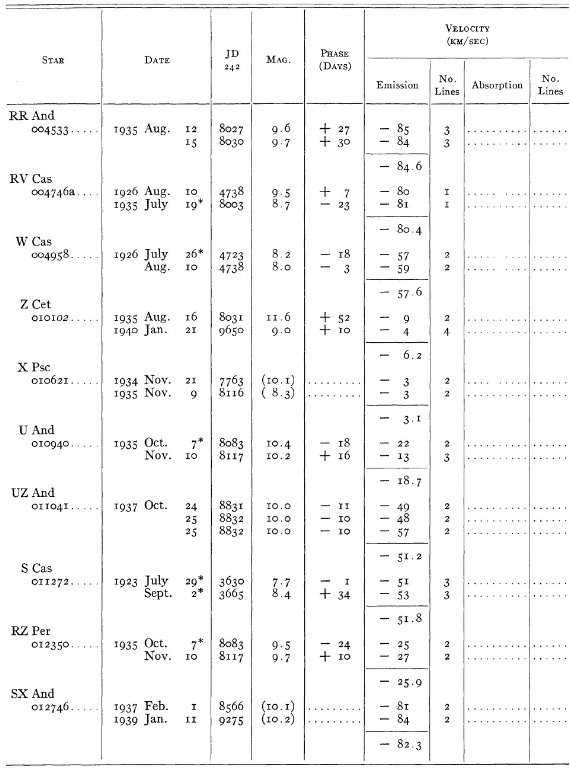
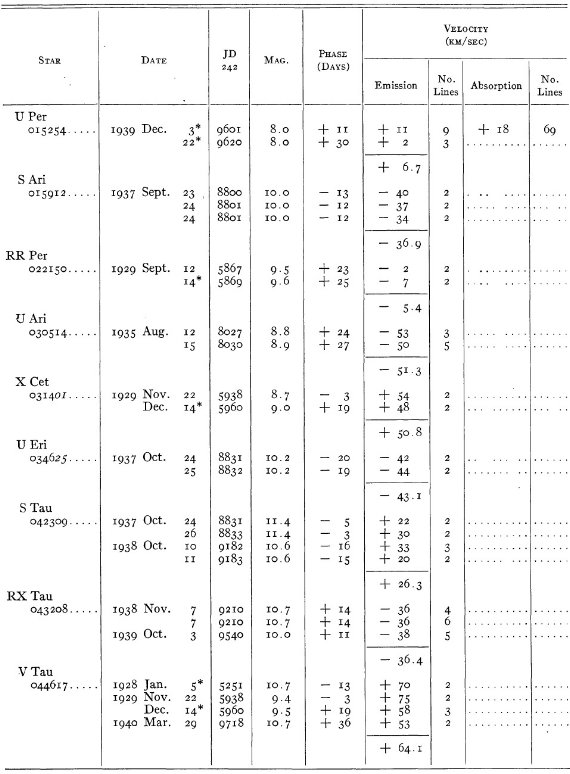
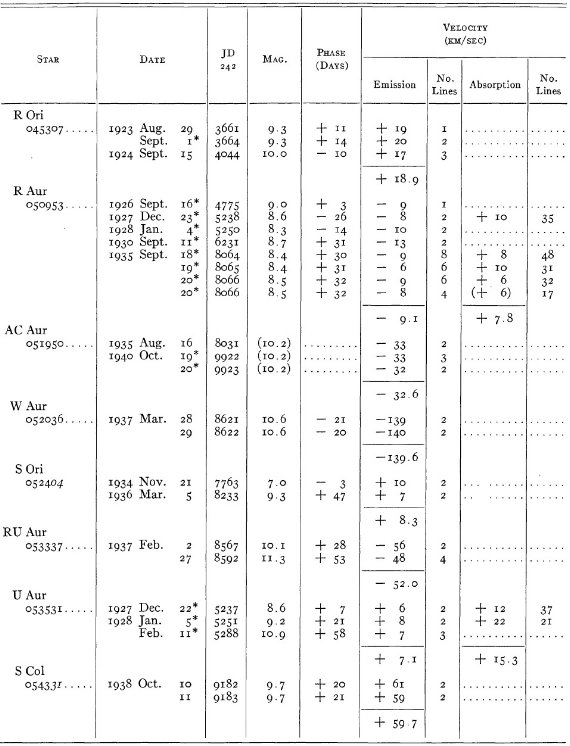
マウントウィルソンで 206 長周期変光星の 618 スペクトルを撮った。
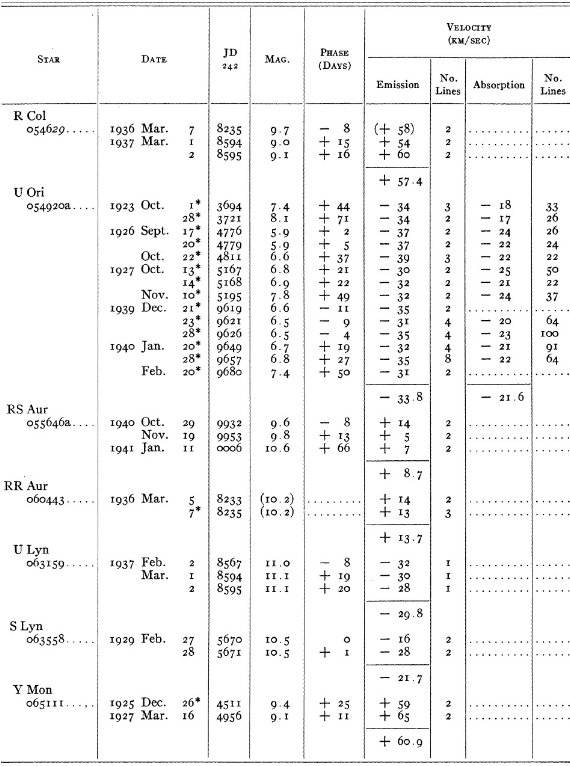
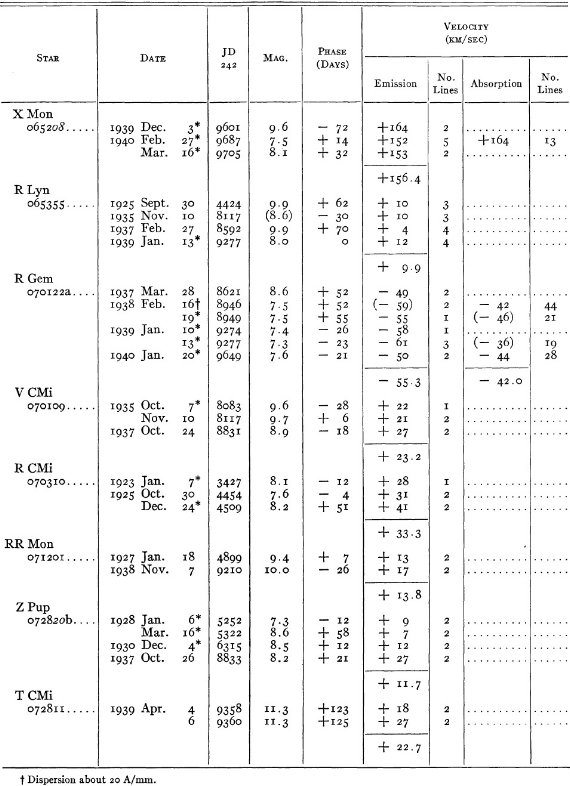
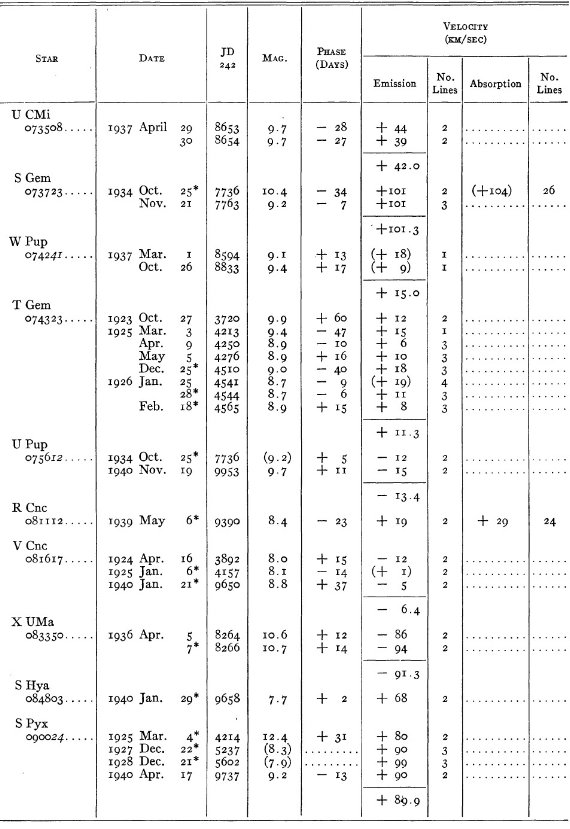
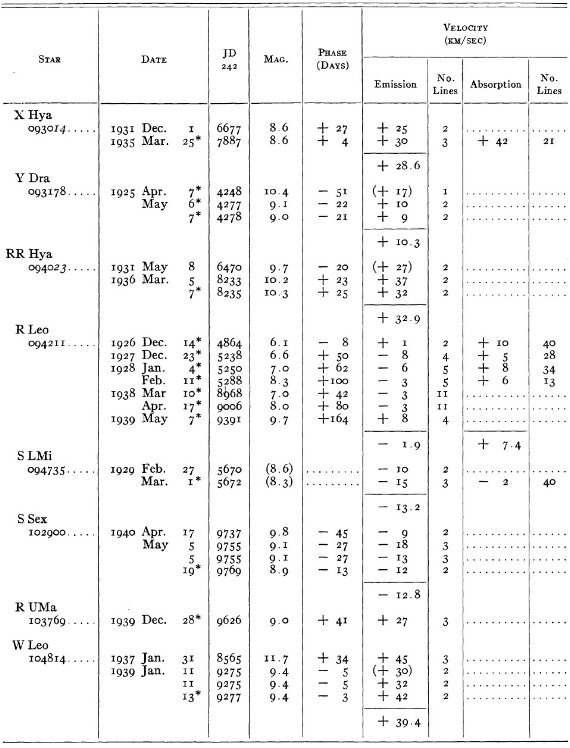
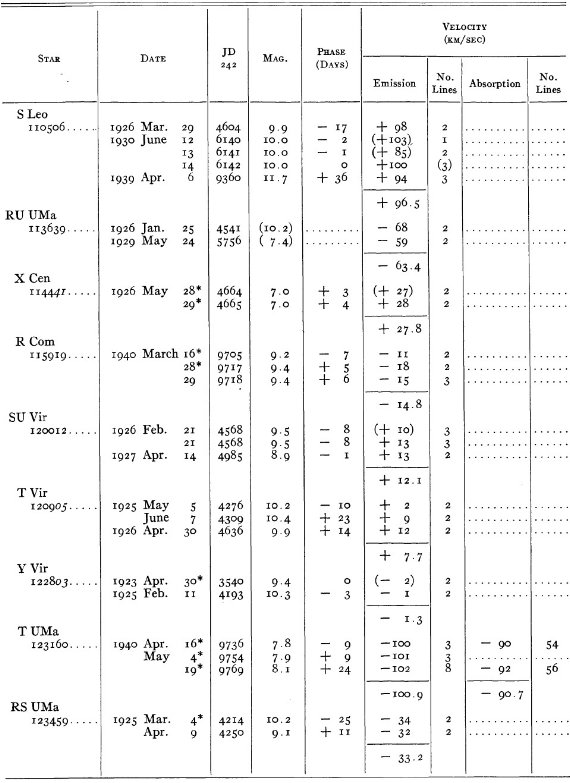
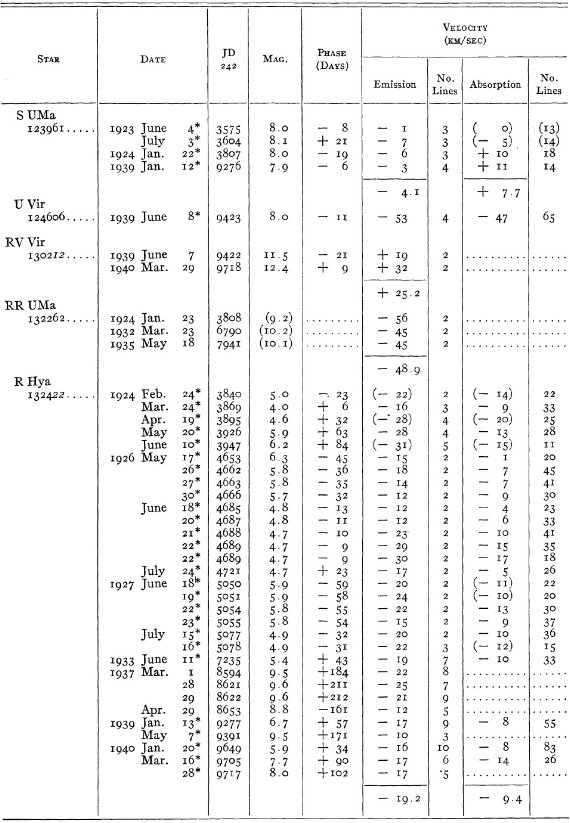
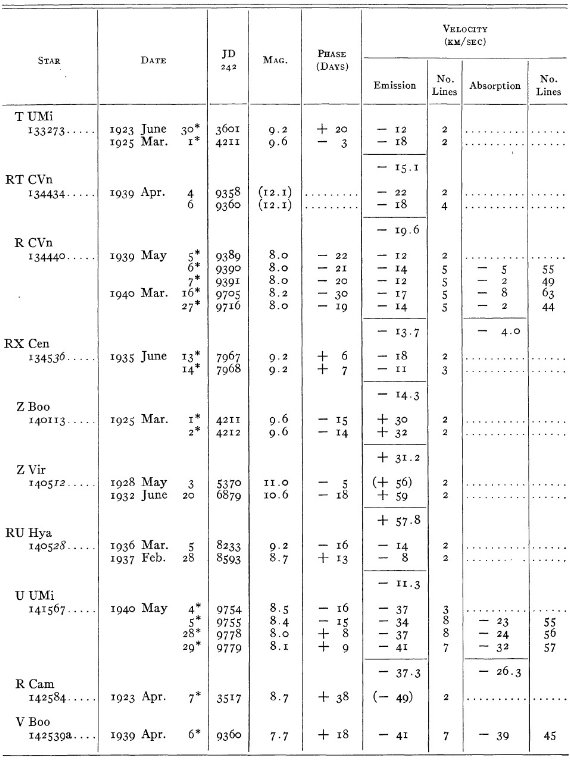
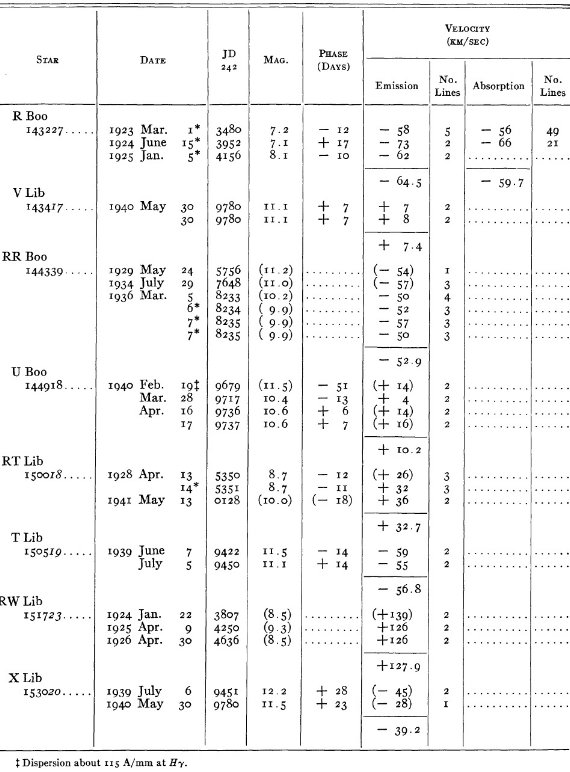
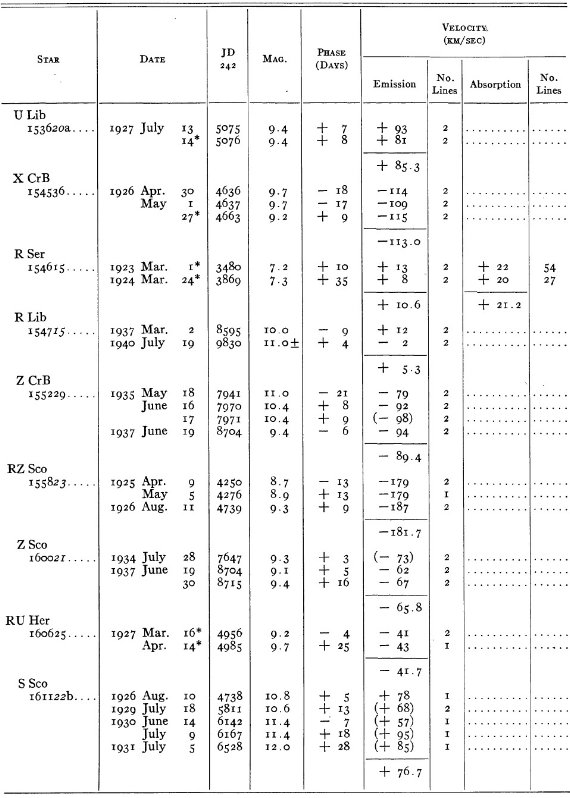
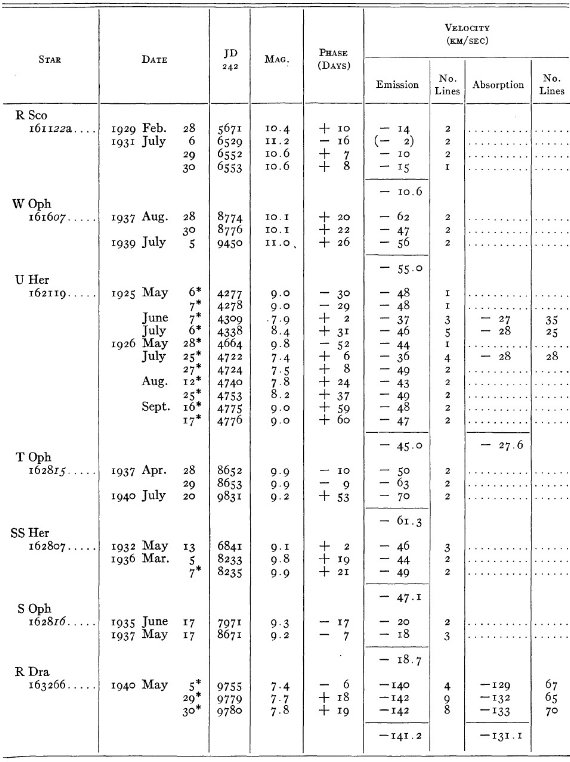
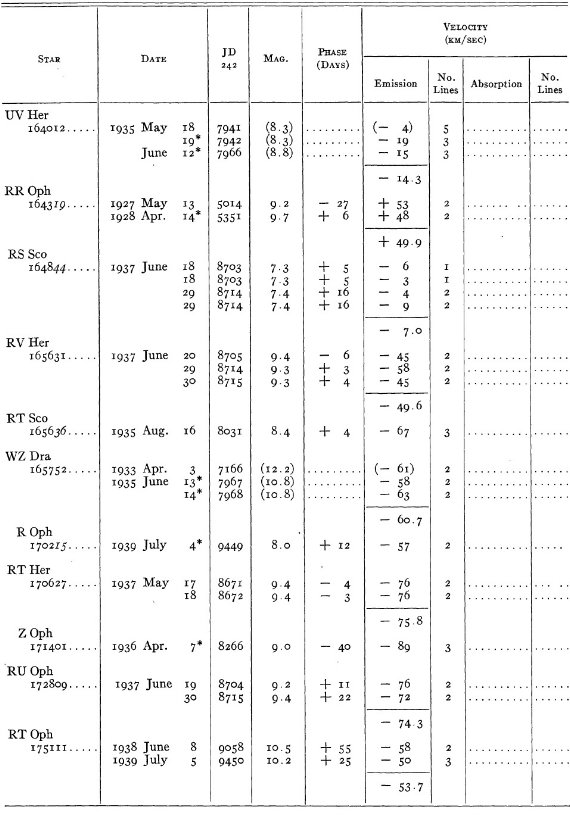
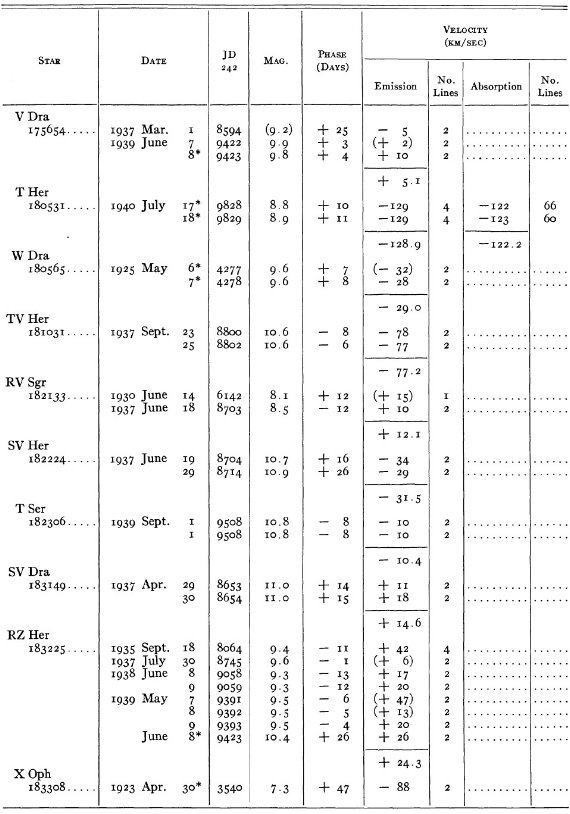
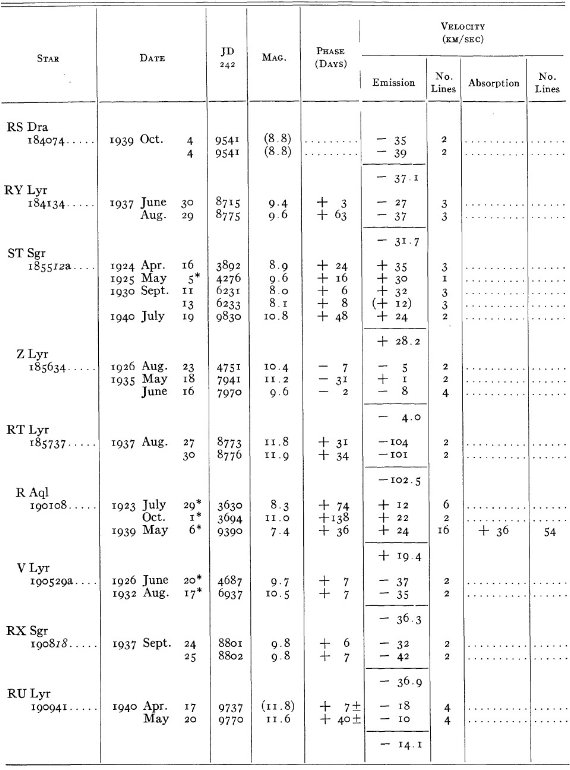
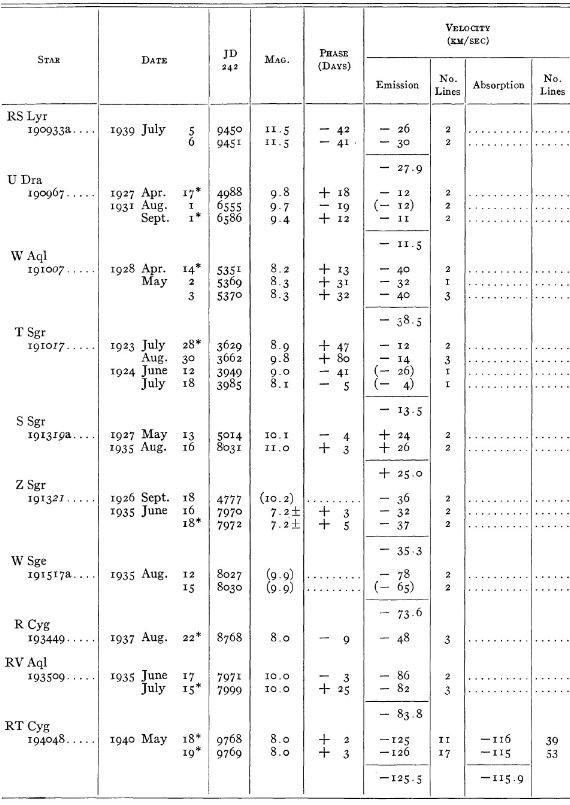
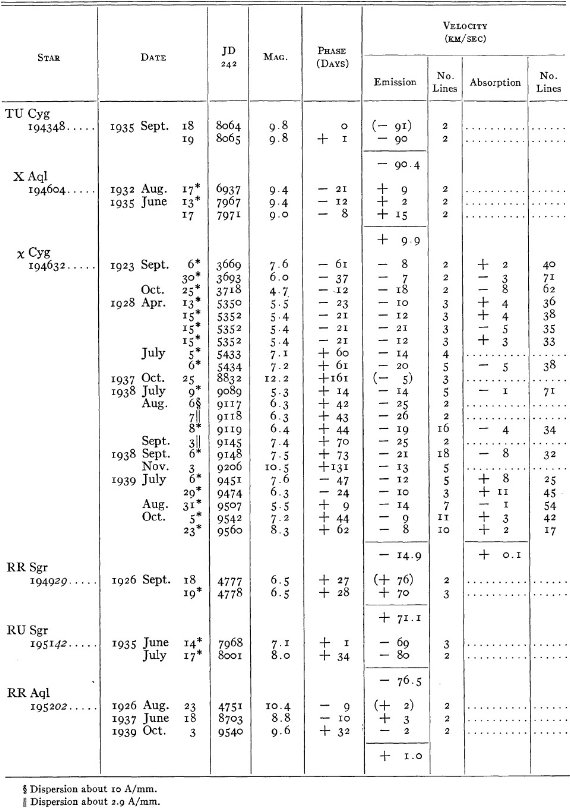
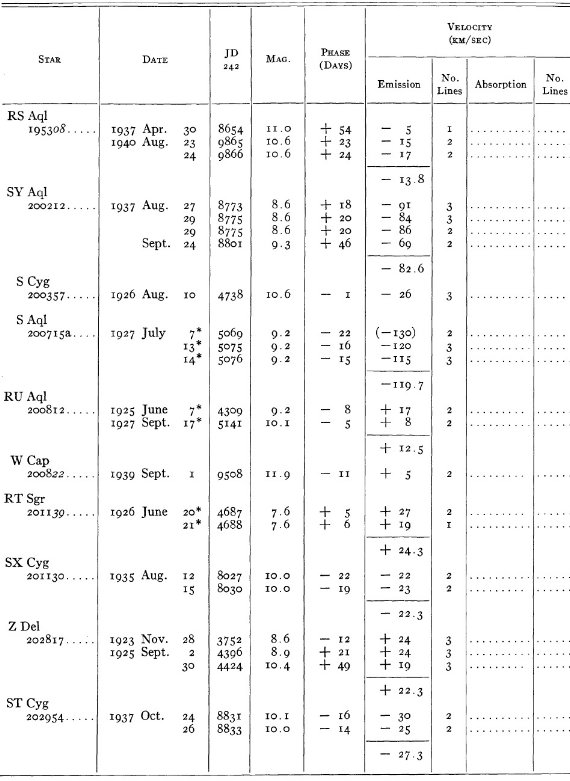
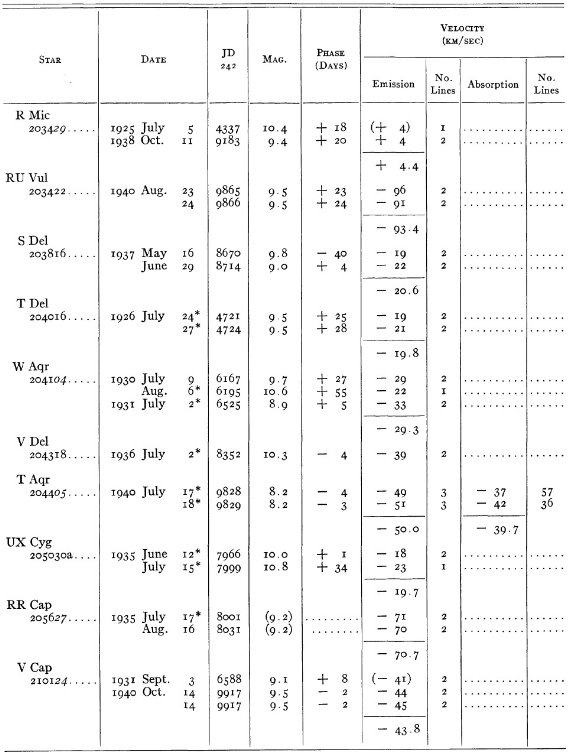
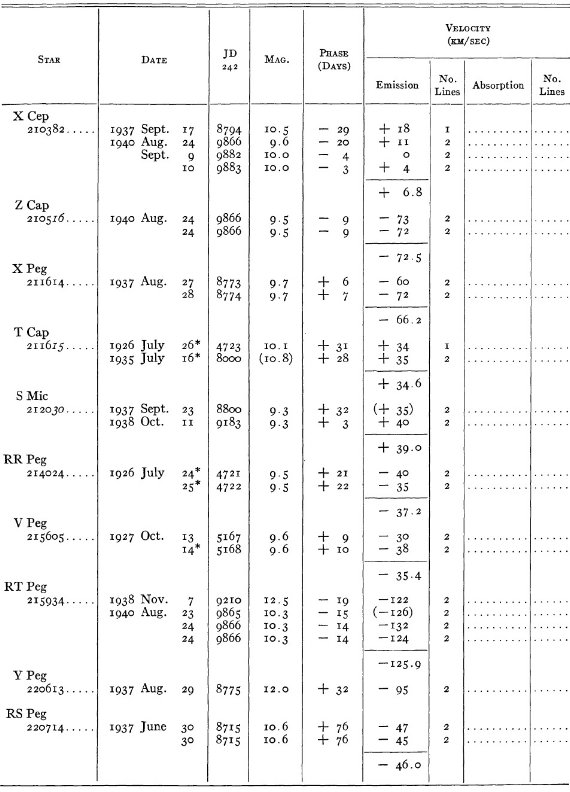
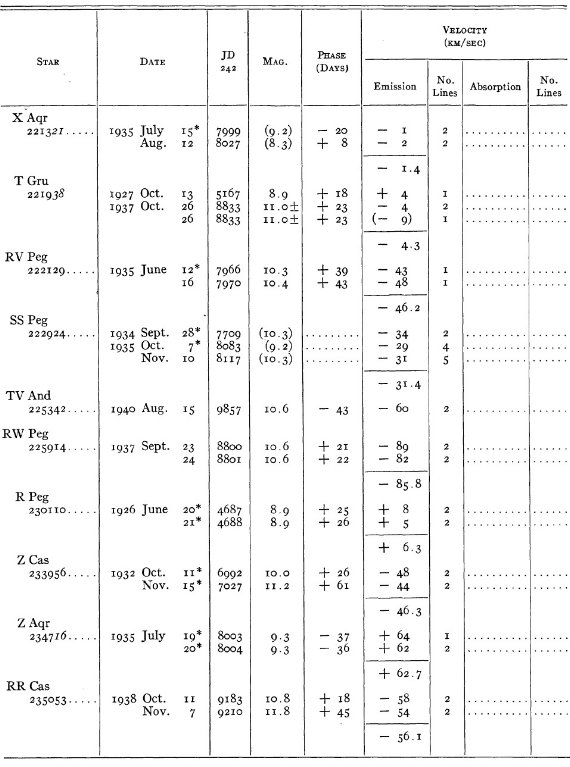
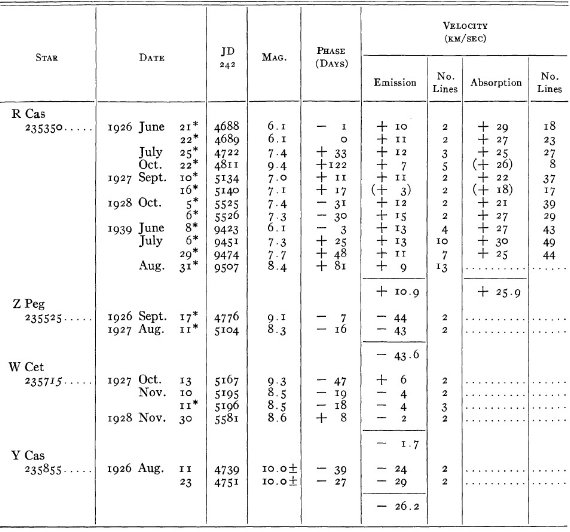
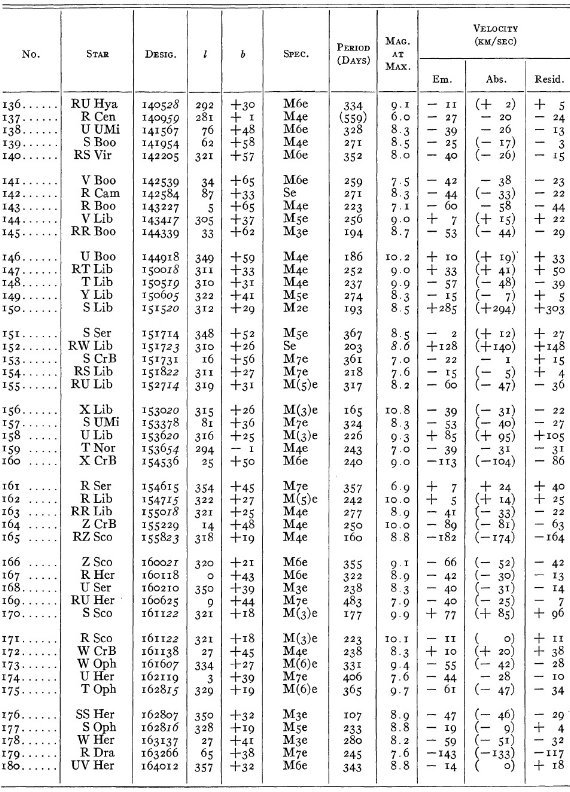
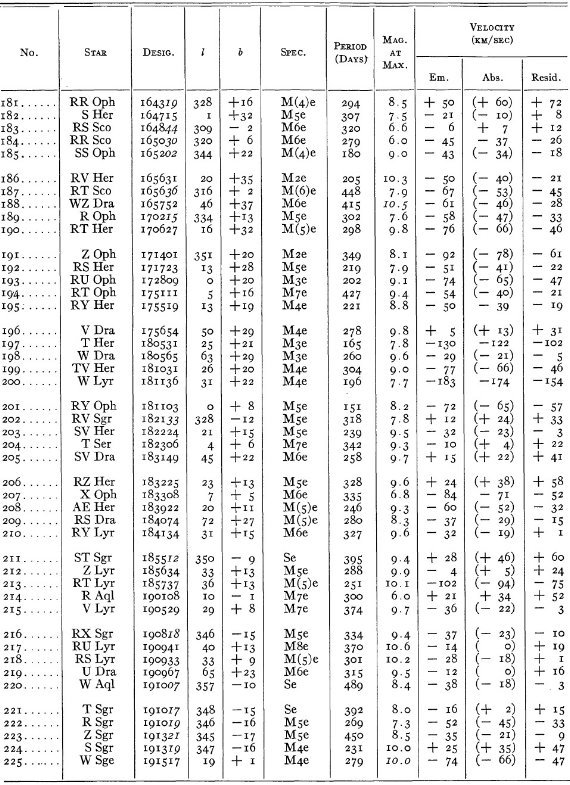
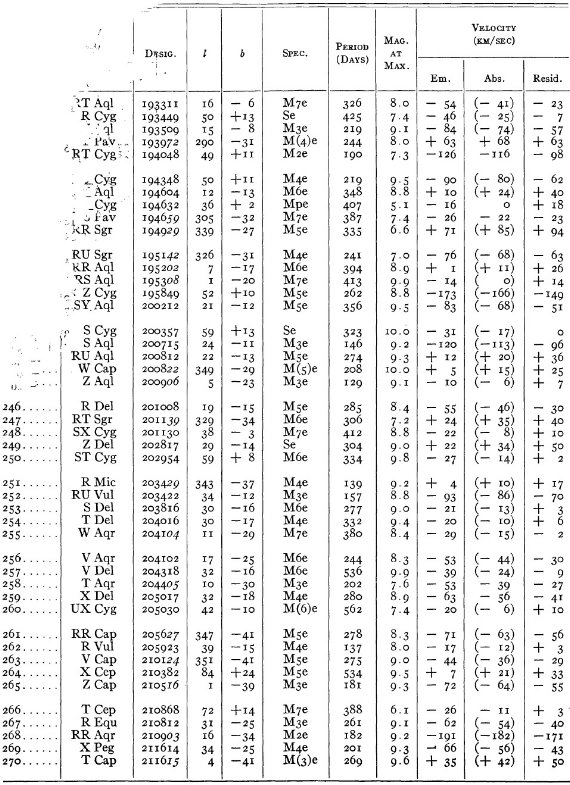
結果は表1に示した。152/206 星は初観測であった。これまでと合わせ 305
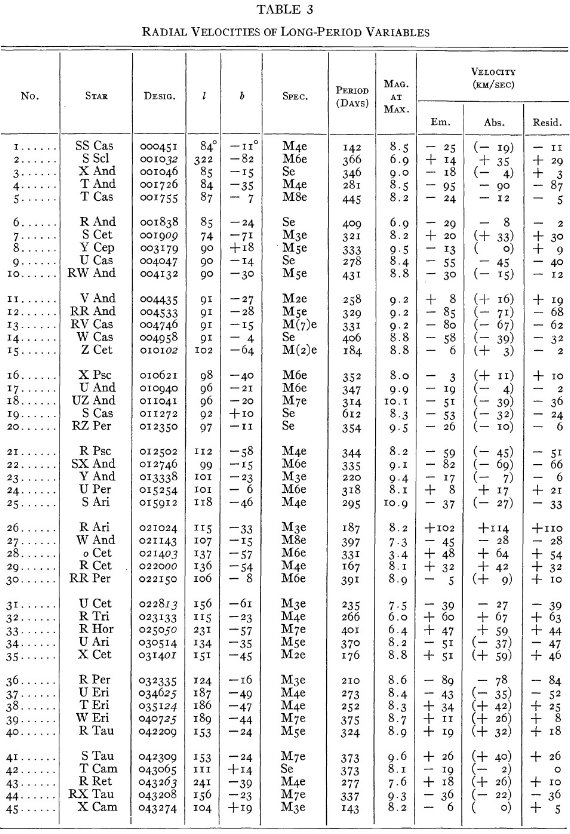
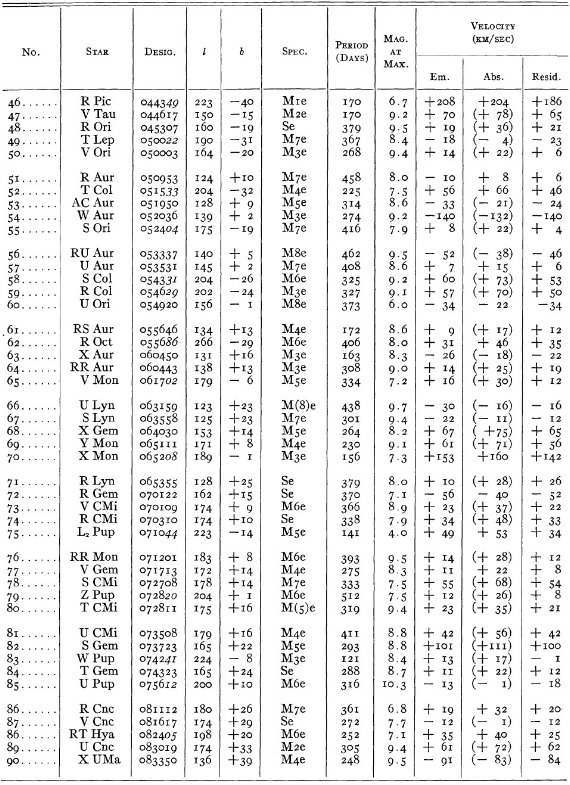
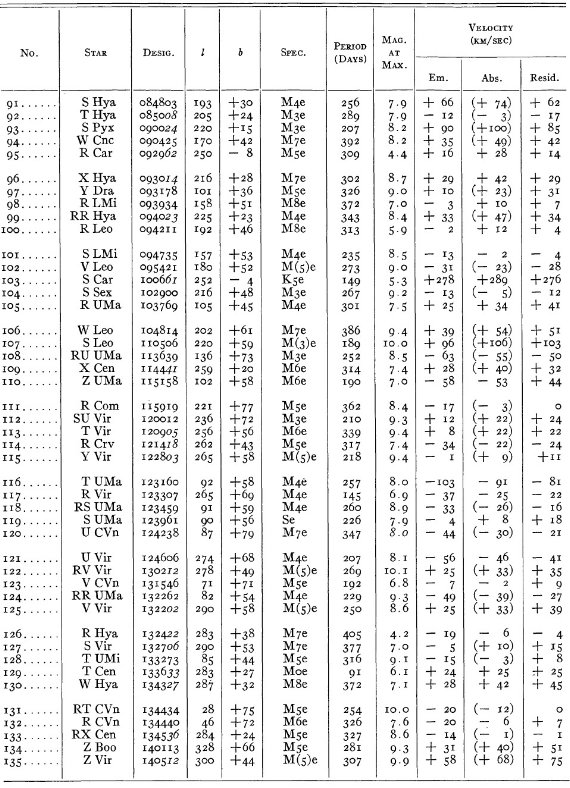
変光星の視線速度全てを表3に載せた。輝線と吸収線との速度差はかなり大
きくなるが、星の運動を調べるには吸収線を使用することを推奨する。
表3の 72 星では吸収線が直接測定された。残りの星は輝線速度に補正を
施して吸収線速度に直した。 太陽運動の補正後の残差視線速度の平均は 36 km/s であった。この値は 短周期、早期型の星ほど大きい。周期との関係ははっきり見て取れる。 P < 300 の 152 星の内、 16 個は 100 km/s を越え、10 個は 80 - 100 km/s であった。一方、P > 300 の 152 星中 100 km/s を越すものはなく、 僅か2つが 80 - 100 km/s であった。平均速度は周期と共に下がり、P = 150 - 199 d の 27 星で 80 km/s が、P > 399 d の 35 星では 17 km/s となる。 |
太陽運動の補正後、 305 星は向点 (α, δ) = (316, 50) で Vo
= 31 km/s の集団運動を示す。残差速度の大きさで星を分けた時、25 km/s 以下の
グループでは Vo = 4 km/s であるのに、残りのグループの Vo = 60 km/s と
なある。同様の結果が星を変光周期で分けた時にも得られる。それに対して、
星を太陽からの距離で分けても Vo は同じくらいであった。集団運動と
散乱速度とのはっきり分かる関係は高速度の非対称性の良い例である。高速度星
の向点は、それらの星が太陽付近の銀河軌道上で天空上のどの方向に向かっている
かを表す。この事実は速度非対称性は非常に小さい回転速度の星が示す効果である
ことを示す。視線方向成分は例外的に大きい。 1923 年に長周期変光星 133 個の視線速度を議論してから、多くの観測が現れた。 今や 282 Me + 24 Se = 305 星になったので再解析を行った。 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
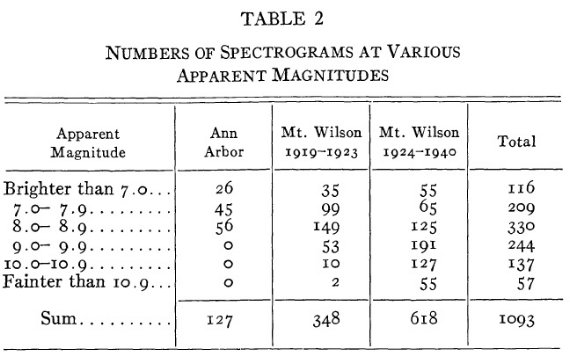 表2.様々な見かけ等級帯でのスペクトル観測数 |
 |
 |
 |
 |
 |
 |
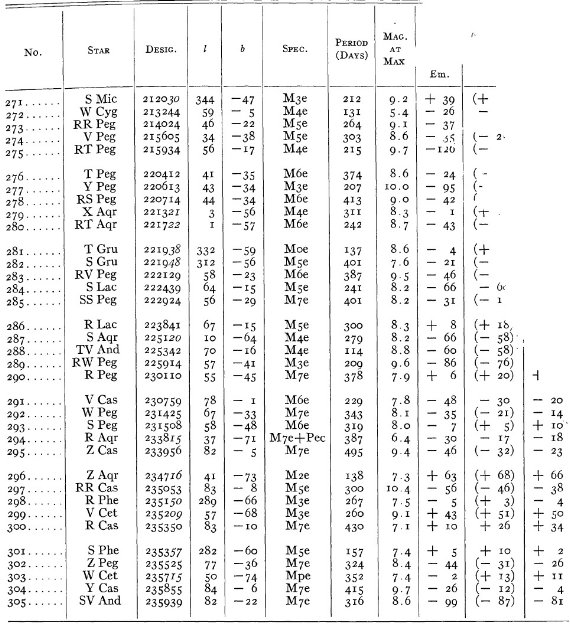 |
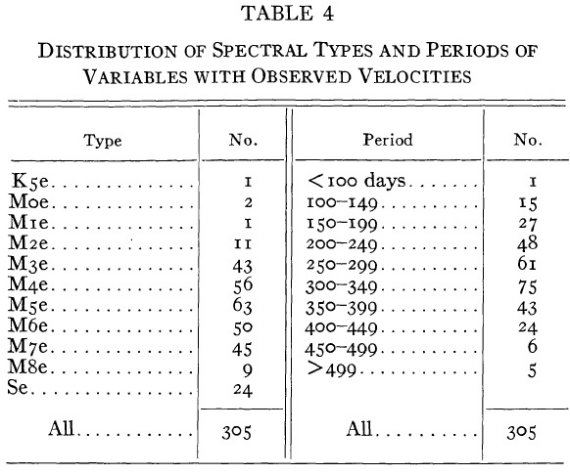 図4.スペクトル型の分布と周期の分布 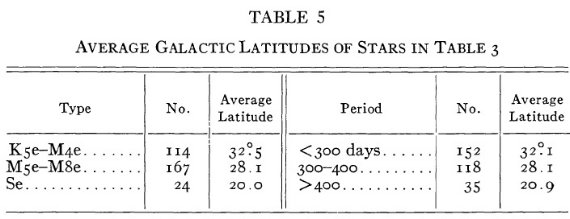 図5.スペクトル型と周期に対する平均銀緯 |
|
短周期の星に大きな速度 以前の論文でも変光星の運動に関して幾つかの興味ある事実が分かった。 残差視線速度は平均 36 km/s で驚くほど大きい。特に面白いのは非常に大きな 速度が M2e - M5e の周期 200 d 付近の星に限られていることである。 残差速度 測定した視線速度はまず地球の公転と自転の効果を差し引き、"太陽中心速度" に直す。これが通常論文に載る値(表3の最後から2番目)である。第2の補正 では数百に及ぶ星集団の中心速度に対する視線速度を求める。この視線速度を "残差速度" と呼び、表3の最後の列に載せた。 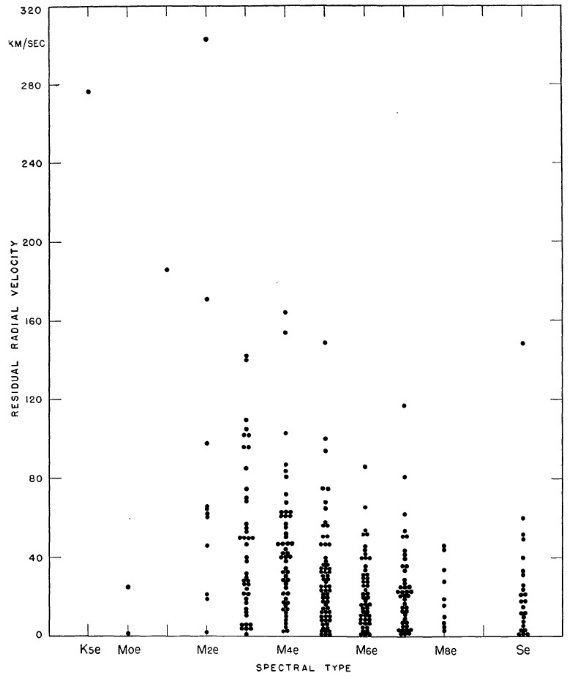 図3.残差視線速度とスペクトル型 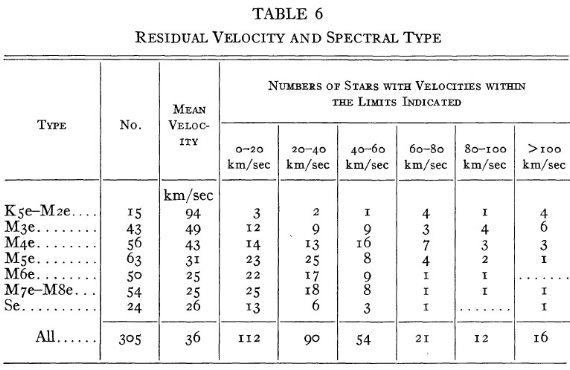 表6.残差速度とスペクトル型 |
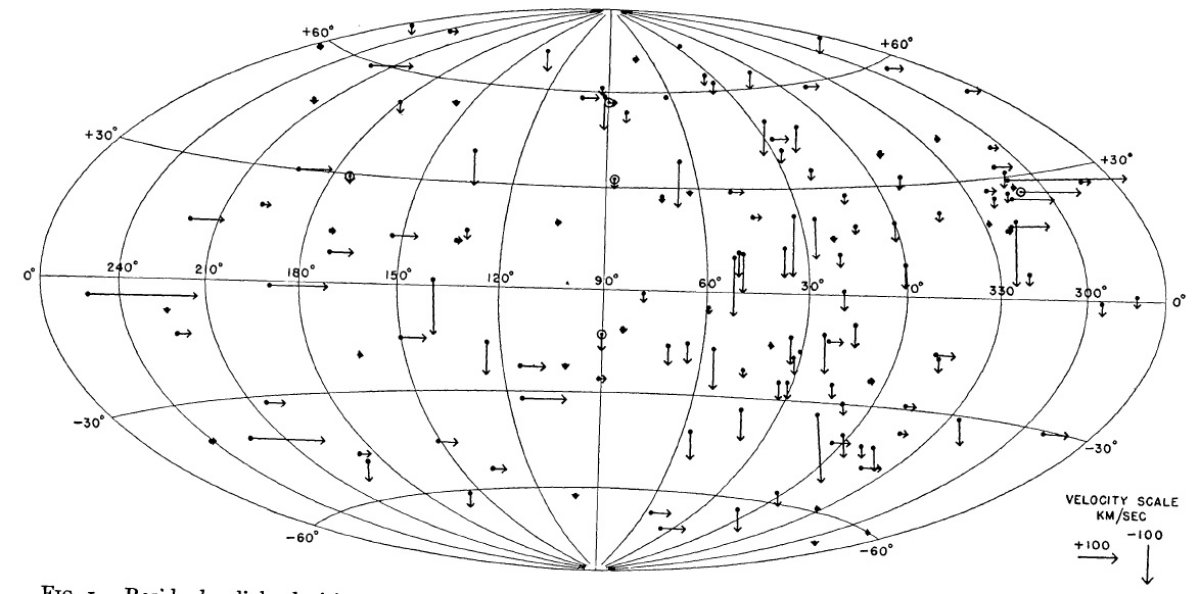
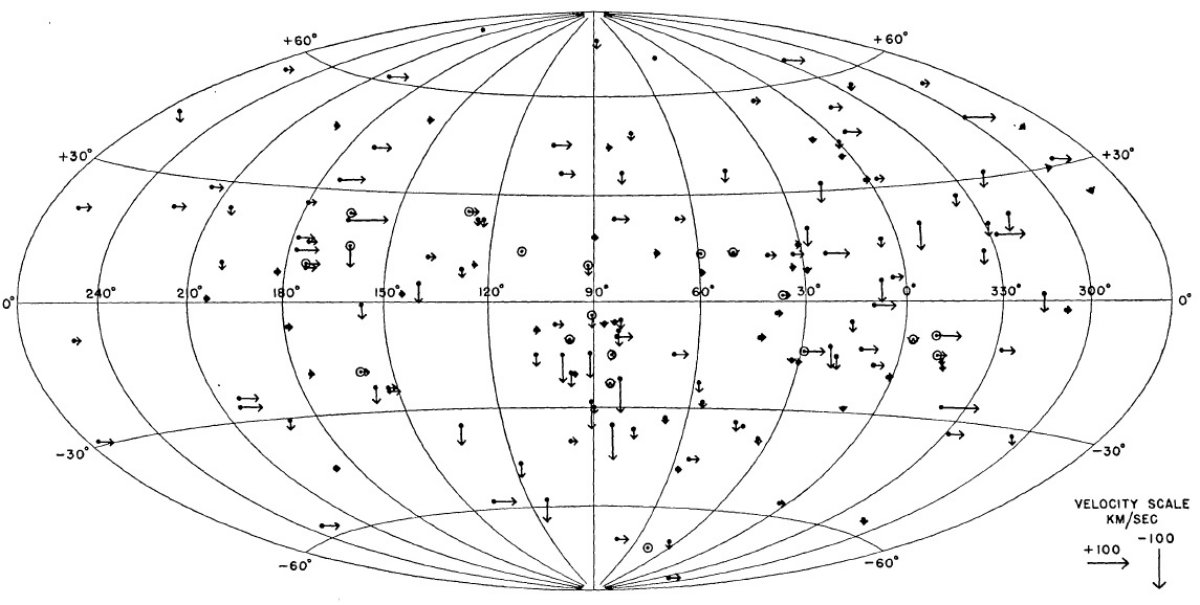
非対称速度分布 星の空間分布と視線速度分布を図1と図2に示されている。速度分布の非対 称性は特に図1によく示されている。そこでは、P < 280 d の星がプロット されている。lI = [0, 90] に接近する星が多く、lI = 220 付近には遠ざかる星が多い。図2には P ≥ 280 d の星を示すが、 速度は小さく、非対称は目立たない。 残差速度の平均 残差速度の arithmetic mean = 36.1 km/s, algebraic mean = -0.9 km/s である。残差速度とスペクトル型との関係を図3に示す。非常な高速が 早期型に現れ、低速星の比率が晩期になるほど高まることがわかる。 詳細は表6を見よ。 (絶対値の平均と正負付きでの平均? ) 残差速度と周期の相関 以前に見出された、高速星は短い変光周期に多いという事実は新しいデータ で確認された。図4にその様子が現れている。残差 100 km/s 以上の星は全て 周期 275 d 以下である。平均速度は周期と共に減少していく。相関はスペク トル型より良い。例外は周期 150 d 以下の星である。 太陽運動 太陽運動は 20 km/s で (α, δ) = (270, 30) の方向と 仮定した。 (図3,4の残差速度は全部正になっている。 絶対値のプロットか? r.m.s. の代行? ) 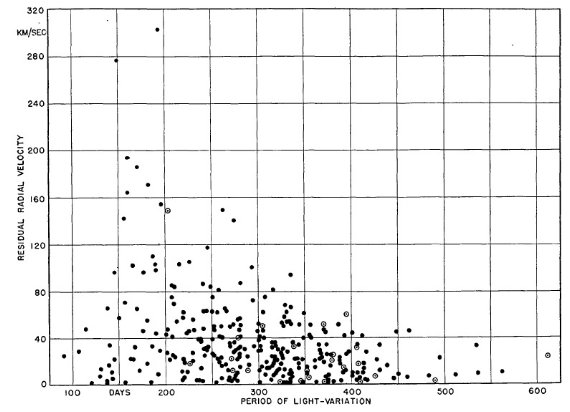 図4.残差視線速度と変光周期。丸= Se, 他は Me. 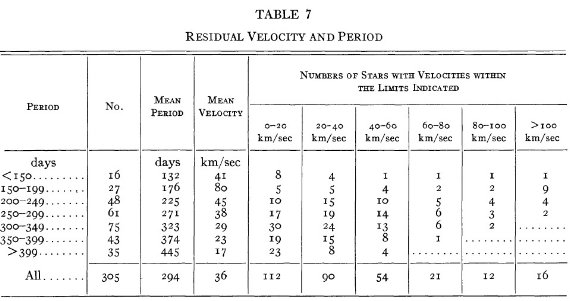 表7.残差速度と周期 |
|
表8=グループ速度 グループ速度の直交成分 x, y, z は最小二乗法で決める。 x cosα cosδ + y sinα cosδ + z sinδ + K = v 表8に様々なグループに対する結果を示す。表には中心速度 Vo, 向点の赤道座標 (Ao, Do) と銀河座標 (Lo, Bo) である。 グループの説明 グループ I は星全部。グループ II と III は残差速度で、グループ IV と V は変光周期で、グループ VI と VII は太陽からの距離で、二つに分けた。各 グループ内で最小二乗の解は K を入れるかゼロに固定するかで二通りの解を 求めた。いくつかの理由で K=0 の方が良さそう。 グループ I, III, V グループ I, III, V の解は似ている。III と V が似るのは高速度と短周期 の相関のため、I は大きいサンプルに引っ張られるためであろう。これらの解 の特徴は Vo が大きく、向点が (l, b) = (56, 0) で太陽周辺の星が銀河系 円周運動で向かう方向であることである。 グループ II, IV グループ II は残差速度が小さいので、Vo = 4 km/s は当たり前である。 向点が太陽運動と一致するのは驚きである。グループ IV も Vo は小さいが 向点は別の方向を向いている。 |
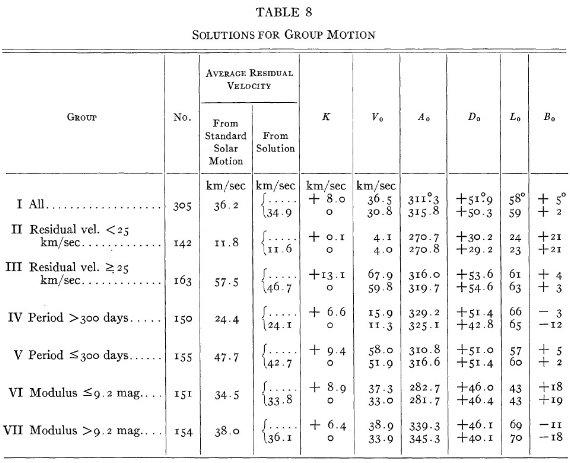 表8.グループ速度の解 |
|
グループ速度 Vo と残差視線速度 図5にはグループ速度 Vo と残差視線速度との関係を示す。良く知られている が、空間速度が大きい星は完全にでたらめな方向を向くのではなく、ある種の 速度非対称性を示す。つまり、ある方向に向けての集団運動を持つ。その方向は 大体、太陽近傍の星が全体として銀河回転するのと反対側である。したがって、 集団運動と見えるのは、実は何らかの理由で回転スピードが遅い星グループの 回転運動の反映である。 |
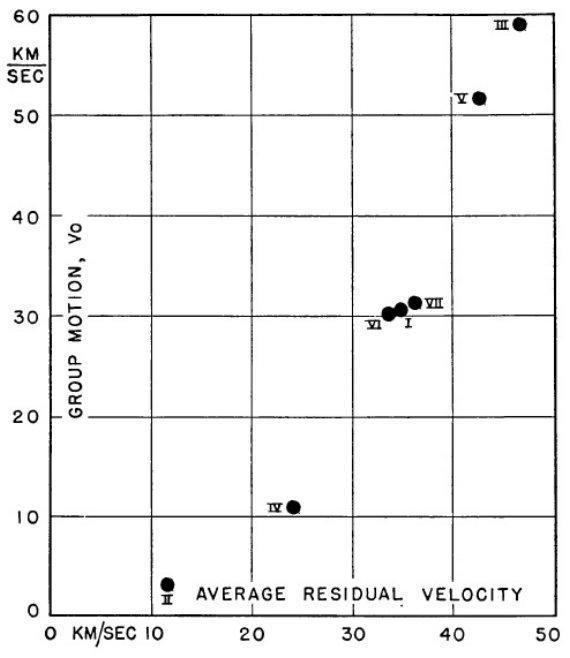 図5.グループ速度 Vo と残差視線速度との関係 |