赤化の較正に、 V = 4.0 より明るく、スペクトル型 G0 - M0, 光度クラス III-IV, III, II - III の57星が観測された。それらは、UBV 測光、カラー指数 C(42-45), C(45-48) が揃っている。大部分の星は 50 pc より内側にあり赤化はないと考える。
赤化フリー G バンド指数 C∗(42-45)
図1は赤化フリー G バンドブレーク指数 C∗(42-45) 対 (B-V) をプロットした。McClure,van den Bergh 1968 (論文I)から採った光度クラス III に対する関係が実線で引いてある。観測に良く合っている。図1上での星の 位置は、見ての通り、有効温度だけでなく表面重力にも依っている。したがって、 赤化を定める前に、表面重力の効果を知る必要がある。
連続光指数 C(45-48)
論文Iでは C(45-48) が晩期型星の表面重力のよい区別指標であると指摘されていた。 図2は C(42-45) - C(45-48) プロットである。クラス IIII 星の関係は、
C(42-45) = 2.222 C(45-48) - 1.761
である。 表面重力効果が図2の分散の主な原因である。
ズレ Δ とは?
図1では Δ C∗(42-45) に表面重力効果があり、 光度クラスで縦に分離することが指摘された。また、図2ではさらに、 C(45-48) が表面重力効果を持ち、プロット点の分散を生じさせている。 そこで、個々の星について平均値からの分散の
Δ C∗(42-45) = C∗(42-45) - C∗(42-45)[図1実線: B-V の関数]
= 図1上、星と実線との縦の差
Δ C(42-45) = C(42-45) - [図2実線: C(45-48) の関数]
= 図2上、星と実線との縦の差
を求め、図3に示した。これらの星は赤化なしと考えるので、星の固有カラーの 間の関係として次の近似式を得る。
Δ C∗(42-45) = 0.430 Δ C(42-45) (2)
図に見られるこのタイトな関係は、図1,2のプロットが示す分散が強く相関しており、 やはり、表面重力が分散の共通の原因であることを強く示唆する。
Δ - Δ 関係
図3の鎖線は、クラス III-IV, III, II-III 間の境界である。したがって、これを 使って光度クラスを決めることができる。クラス II, IV の星の観測は図3の相関 を確認したが、(1)暗い星は赤化調査に役立たない、(2)明るいが数が少ない 理由により扱わない。
赤化の導出
メタル量効果を得るため、図1,2に [Fe/H]<-0.4 の低メタル星を白丸で示 した。強ライン星はクロスである。図1、2、3で、これら低メタル、高メタル星 は通常星と同じ平均ラインに乗る。したがって、図3で星から実線へ赤化ベクトル を引いて赤化を決める方法はメタル量によって影響を受けない。図3で、メタル量 効果は表面重力効果と同じ方向に沿って星をずらすのである。
しかし、Δ - Δ 図にプロットするためには 赤化を戻した、 (B-V), C(45-48) が必要じゃないのか? いいのかなあ。
UBV が不十分なわけ
図4には同じ星を, U-B, B-V 面上にプロットした。低メタル星と高メタル星が Scmidt-Kaler 1065 のクラスIII固有直線を挟んで両側に分かれて位置することが 判る。これが、何故 UBV 測光のみでは高緯度晩期型星の赤化を決められないかと いう問いに対する解答である。
Δ C(42-45) と式(2)を用いると、 Δ C∗(42-45) が得られる。この値を表面重力効果をによるズレと考えて、補正した C∗ (42-45) を (B-V) に対して図5でプロットした。図5はこの補正した Δ C∗(42-45) と B-V の関係が非常にタイトであることを 示す。
この「補正」の意味が判らない。なぜいきなり図2から Δ C∗(42-45) へ行かないで、 Δ C(42-45) を経る のかもはっきりしないが、Δ C∗(42-45) で戻したら、 そりゃ、平均線に戻るということだから、分散は消えてしまうだろうけど。
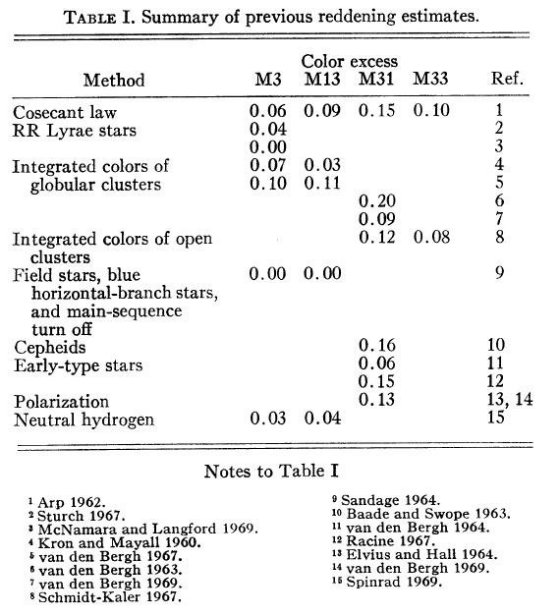
表1 赤化のまとめ。
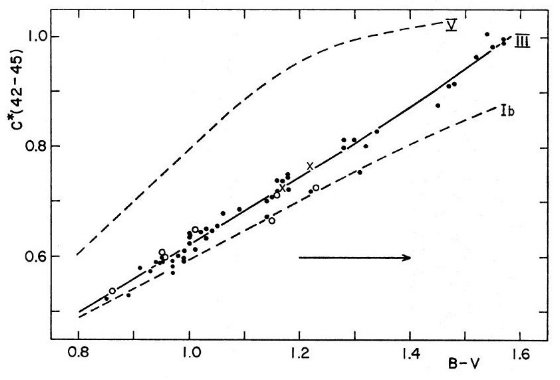
図1 赤化フリー G バンドブレーク指数 C∗(42-45) 対 (B-V) プロット。
黒点:光度クラスIII。白丸:[Fe/H] < -0.4 の巨星。
クロス:吸収線の強い星, μ Leo, α Ser.
実線は論文Iより。鎖線はクラス V と Ib 星を近似。矢印:E(B-V)=0.2
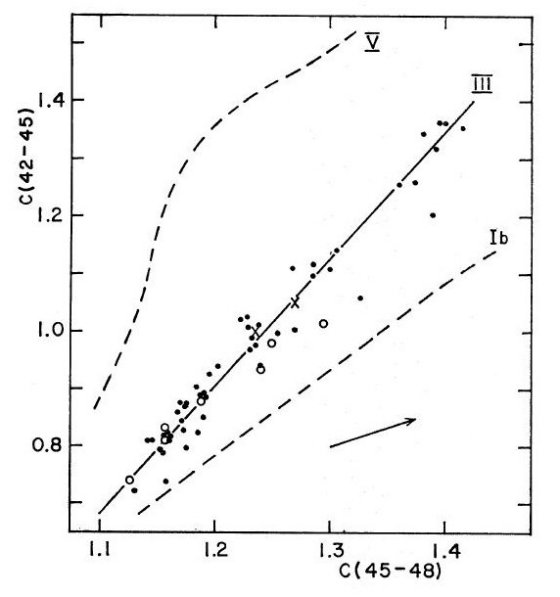
図2 G バンド指数 C(42-45) 対 連続光指数 C(45-48)。
図1と同じ星をプロットした。マークの意味は図1に同じ。
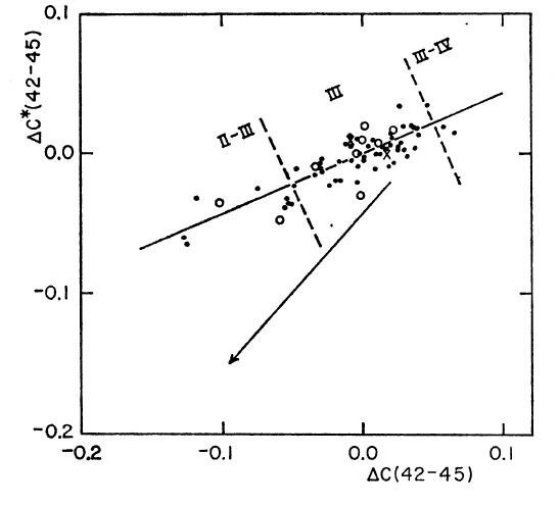
図3 クラスIIIの星に対する平均線、からの残差 Δ C∗ (42-45) と Δ (42-45)
の比較。黒点はクラス II-IV,III, II-III, クロスは強吸収線星。
矢印は E(B-V) = 0.2 の赤化ベクトル。
星の赤化は、赤化ベクトルと平行な直線を (Δ,Δ)平均線まで
伸ばして求める。
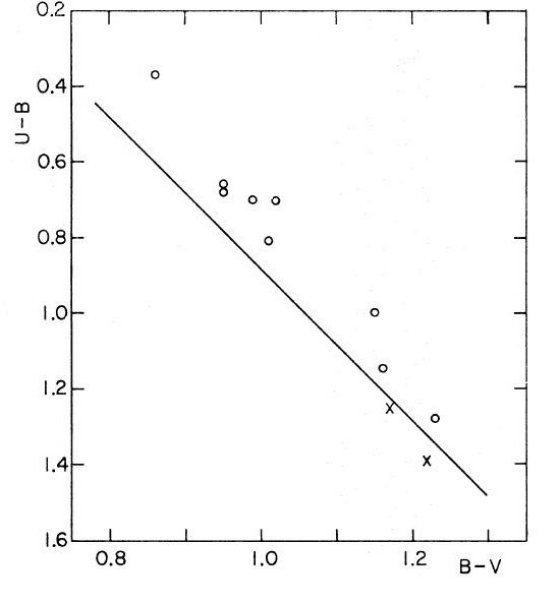
図4 同じ星の U-B, B-V プロット。実線は Schmidt-Kaler のクラス III ライン。
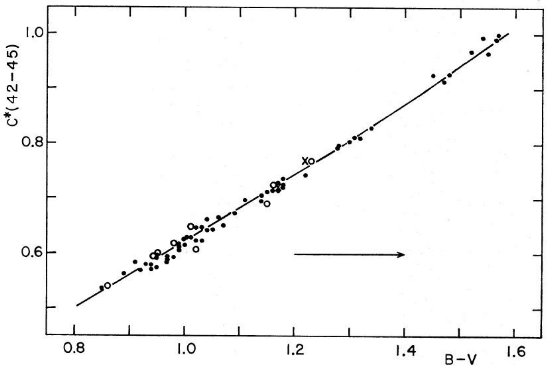
図5 図3から出した残差 Δ C∗(42-45) を用いて表面重力
効果を補正した C∗(42-45) を (B-V) に対してプロット。
マークの意味は前図に同じ。