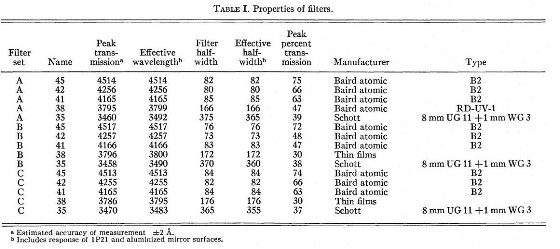
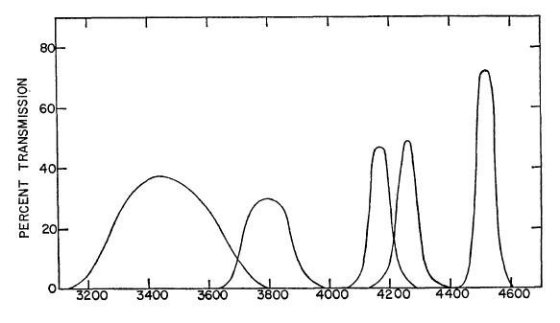
星の選択
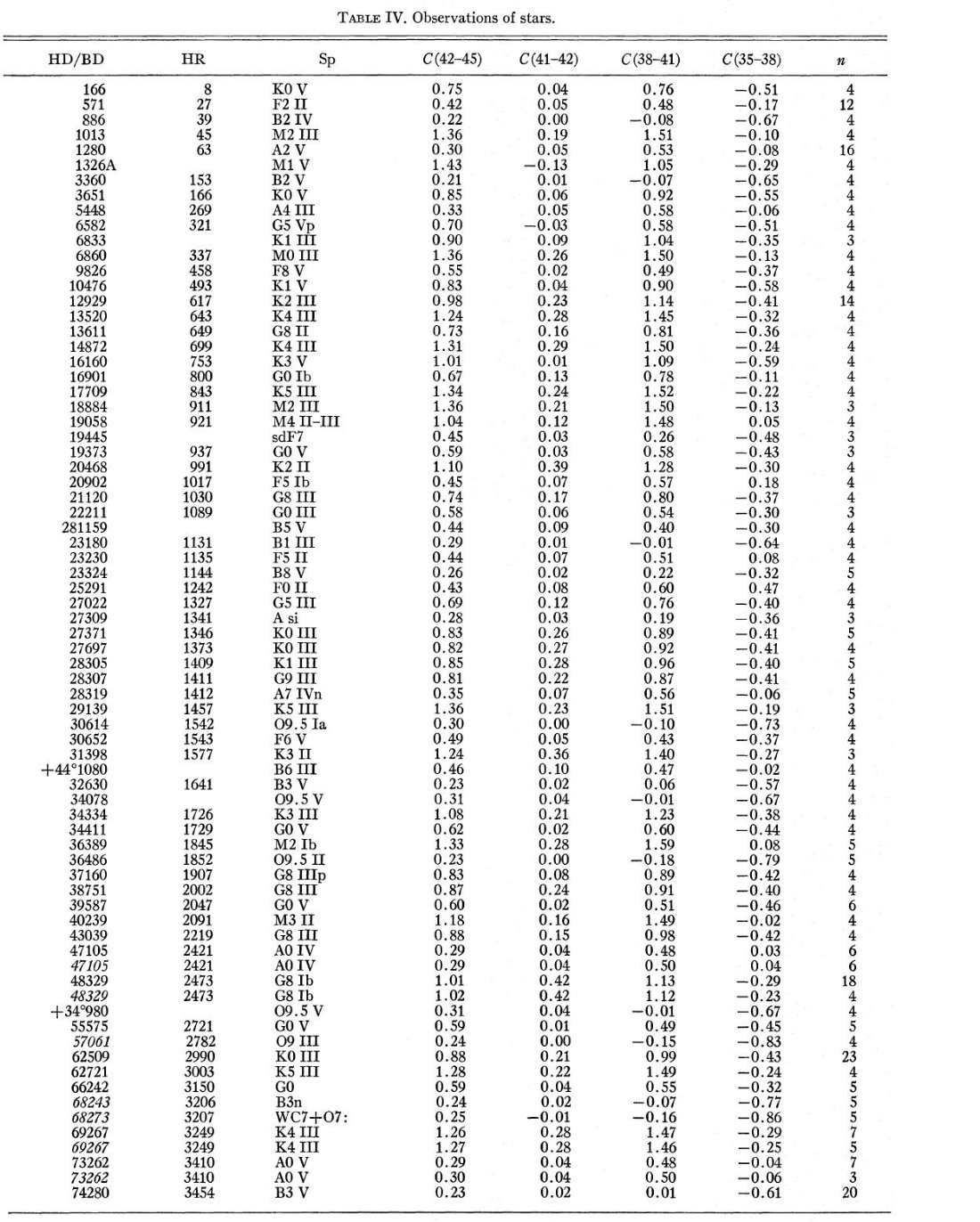
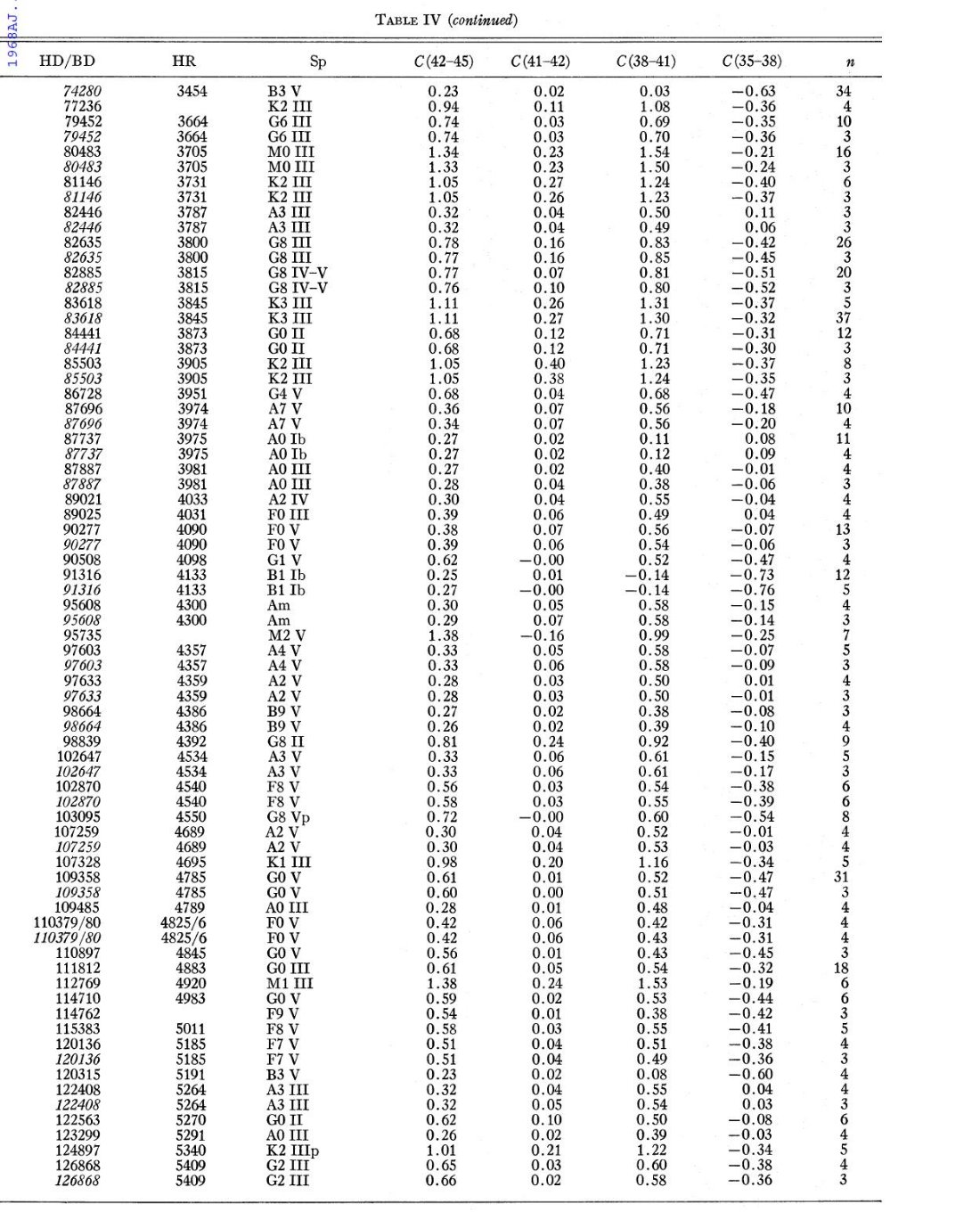
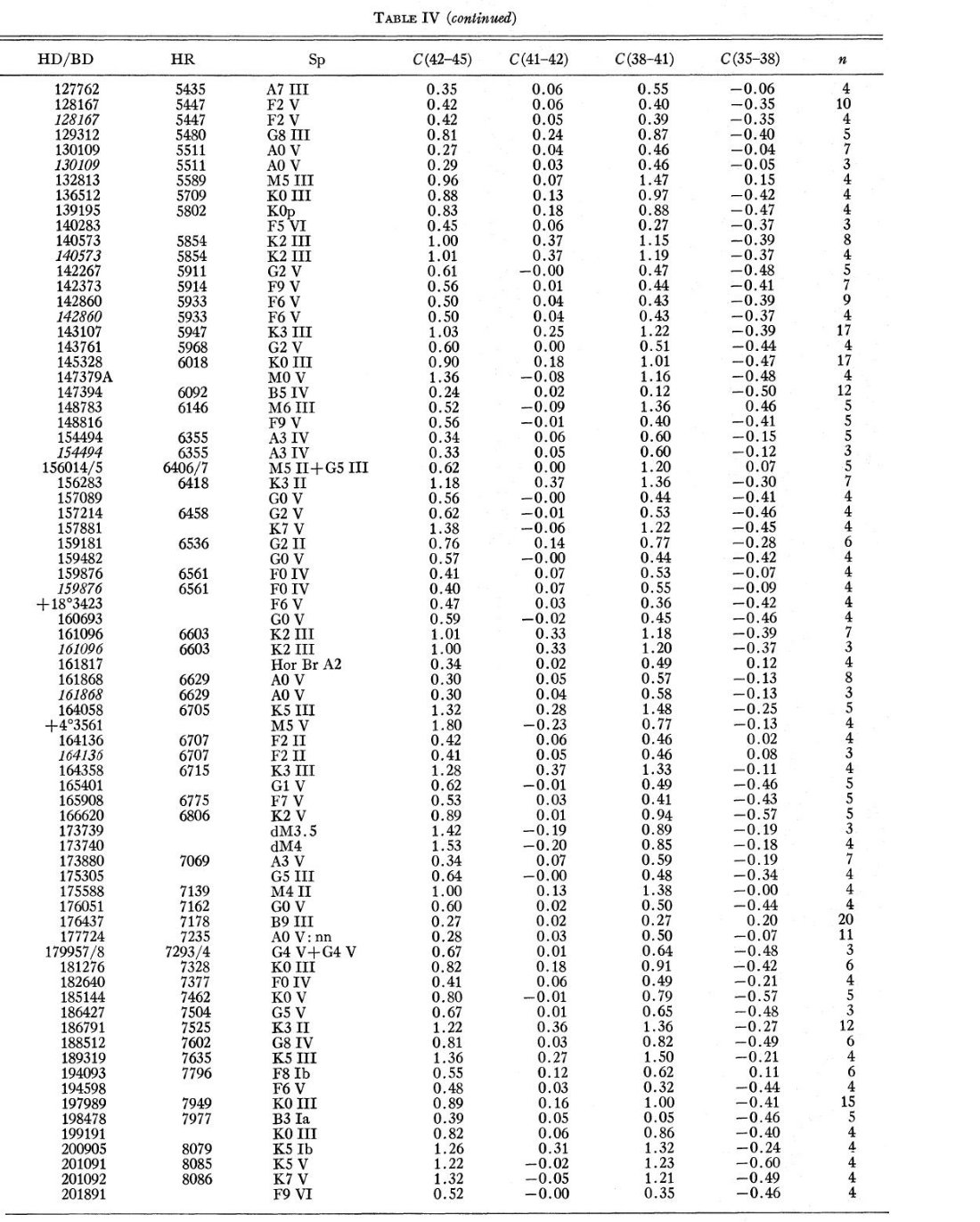
210の観測星の選択には以下の基準が用いられた。リストは表4にある。
(a) 出来るだけ明るい。
(b) O9 - M6 に渡る。
(c) 高メタルと低メタルの両方。52星は[Fe/H]が既知である。
(d) 異常星を幾つか含む。
赤化フリー色指数の定義
多くの星で赤化は不明である。従って赤化フリー色指数の利用が望ましい。
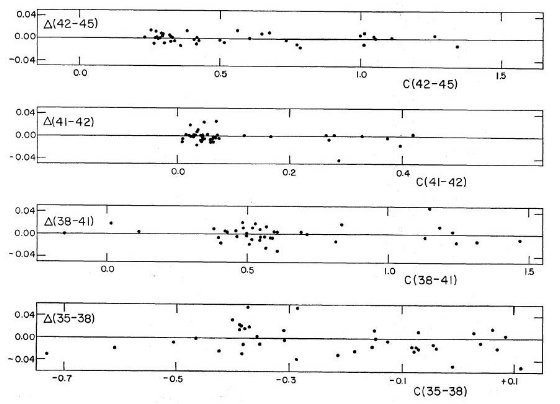
C∗(35-38) = C(35-38) - 0.306(B-V)
C∗(38-41) = C(38-41) - 0.318(B-V)
C∗(41-42) = C(41-42) - 0.066(B-V)
C∗(42-45) = C(42-45) - 0.234(B-V)
図3−6はこれら指数とスペクトル型の関係をプロットしている。
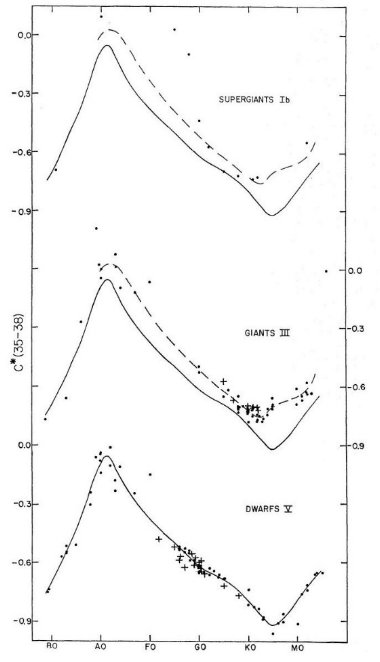
C∗(35-38)
図3は C∗(35-38) がスペクトル型G,K, M型で矮星と巨星
をまあ良く分離することが判る。どのタイプでもこの指数はメタル量の影響は少ない。
F型付近でこれは光度に著しく敏感である。
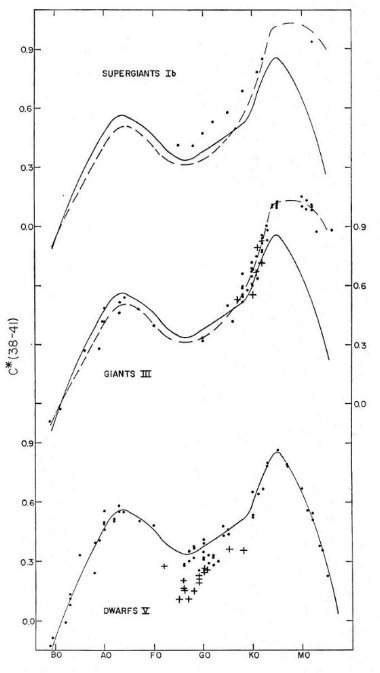
C∗(38-41)
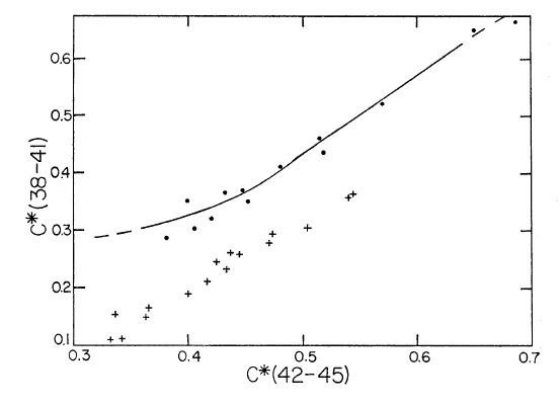
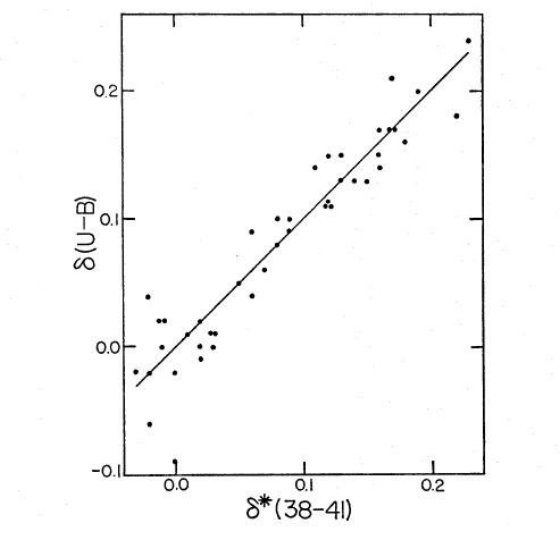
図4は C∗(38-41) が F, G 型矮星でメタル量に鋭敏なことを
示す。4000 A 不連続を測る指数なのでこれはある程度予期されたことである。
F,G型では、巨星と超巨星を分離するある程度よい指数である。
C∗(41-42)
図5は C∗(41-42) が CN の 4216 A バンド強度を測っている
ことを示す。この指数は、晩期型星で光度クラスの分離に有用である。しかし、この
指数のみでは矮星と非常に低メタルの巨星を区別できないことを強調しておく。どち
らもCNが弱いのである。μ Leo や α Ser のように CN が異常に強い巨星
はこの指数で容易に検出できる。
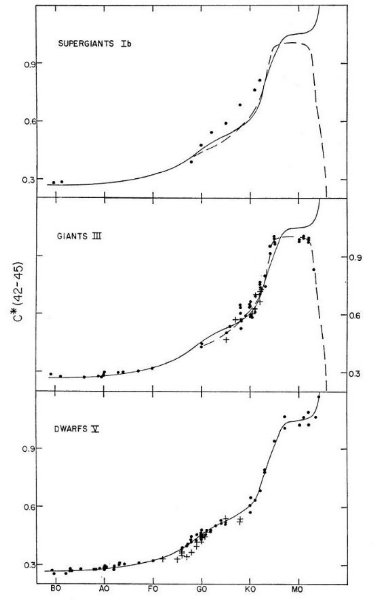
C∗(35-38)
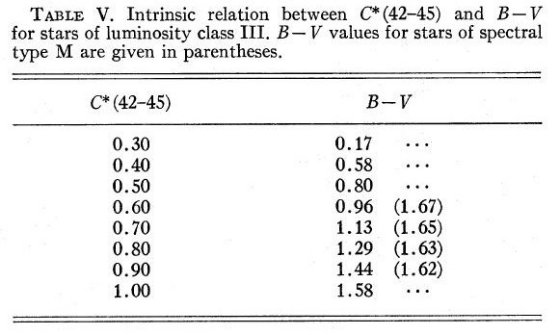
図6は C∗(42-45) が K5より早期の星のスペクトル型を
良く表わすことを示す。
| |
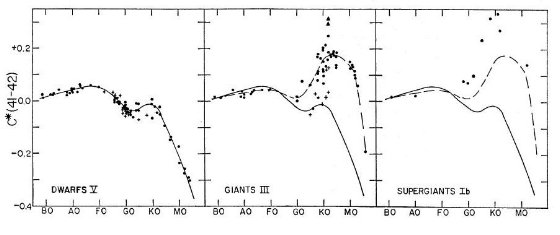
図5 C∗(41-42)は 4216 A より短波長側のCN吸収を測る。
光度により大きく変化することが判る。高速度星は指数が弱い。
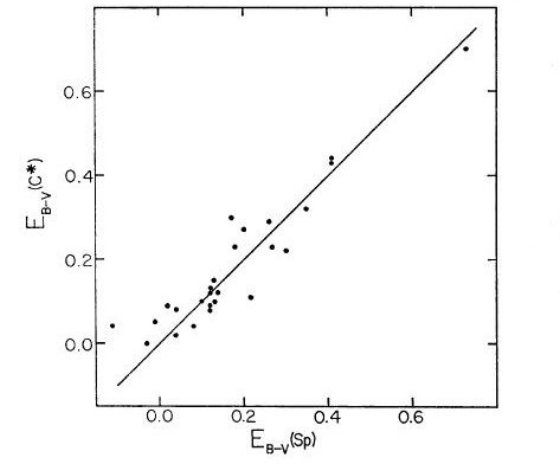
赤化フリー色指数の応用
赤化フリー色指数を実際に使用した3例を以下に示す。星のデータは、
| 星名 | C∗(35-38) |
C∗(38-41) |
C∗(41-42) |
C∗(42-45) |
|---|
| HD 12929 | -0.76 | +0.77 | +0.16 | +0.71 |
|---|
| HD 166 | -0.74 | +0.52 | -0.01 | +0.57 |
|---|
| HD 103095 | -0.77 | +0.36 | -0.05 | +0.54 |
|---|
HD 12929
C∗(42-45) = +0.71 から、この星が光度クラス III-V
ならスペクトル型は K2 ±1, 光度クラス Ib ならスペクトル型は G9
±2 である。CN 強度指標の C∗(41-42) = +0.16 から
光度クラス IIIである。C∗(35-38), C∗(38-41)
も K2 ±1 の分類と合致する。したがって、K2III である。
HD 166
C∗(42-45) = +0.57 から、この星が光度クラス V, III
ならスペクトル型は G8 ±2, 光度クラス Ib ならスペクトル型は G4
±2 である。CN 強度指標の C∗(41-42) = -0.01 から
光度クラス V が示唆される。 C∗(38-41)はメタル量が正常である
ことを示す。したがって、G8 ±2 V である。この結論は MK タイプ K0 V で
紫外超過 δ(U-B) = 0.00 と一致する。
HD 103095 = Groombridge 1830
C∗(42-45) = +0.54 から、この星が光度クラス V
ならスペクトル型は G6 ±2, 光度クラス III ならスペクトル型は G7
±2, 光度クラス Ib ならスペクトル型は G3 ±2 である。CN 強度
指標の C∗(41-42) = -0.05 から Ib は除外され、正常 V か、
非常に低メタルの巨星を示唆する。C∗(35-38) は G7 ±2
は合わないことがわかる。 したがって、G6 ±2 である。このスペクトル型
だと、C∗(38-41) = +0.36 はこの星が大きな紫外超過を持つ
ことを示す。したがって、最後の結論は sdG6 ±2 である。MK タイプ
G8Vp で紫外超過 δ(U-B) = +0.17 と一致する。
|