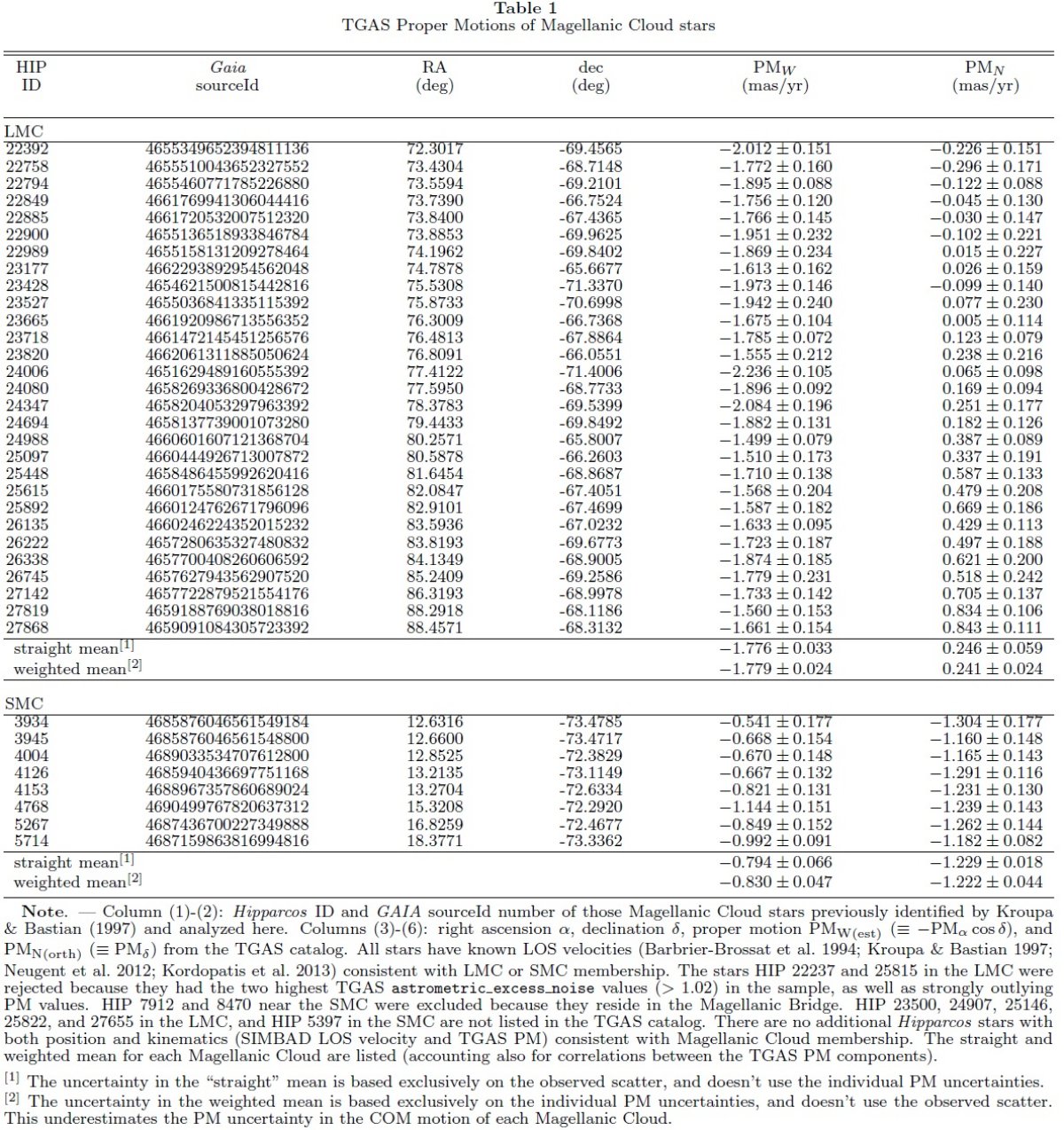
| Gaia DR1 を用いて LMC/SMC の固有運動(PM)を調べた。そのために LMC で 29 個、SMC で 8 個のヒッパルコス星の Tyco-Gaia Astrometric Solution (TGAS) 固有運動を用いた。西、北方向の固有運動は LMC が (μW, μN) = (-1.872±0.045, 0.224±0.054) mas/yr, SMC が (μW, μN) = (-0.874±0.066, -1.229±0.047) mas/yr である。これらの結果は HST が得た結果と大体等しい。 TGAS の値は HST と独立な手法で求めたもので、この結果は両者の解析の確実性を 示す。 | また、HST の結果と一致することだが、TGAS LMC PM 速度場は時計回りの 回転を示す。LMC 円盤の回転には 108 年以上かかる。若い星の回転曲線の振幅 は視線速度観測から予期されていたものと一致する。固有運動と視線速度の比較から 運動学的 LMC 距離指数 m-M = 18.54±0.39 が得られた。 |
|
TGAS カタログ Gaia DR1 では ガイアとヒッパルコス Tycho-2 カタログに共通する星の固有 運動(PM)を載せている。この共通星のみを集めたカタログは Tycho-Gaia Astrometry Solution (TGAS) カタログと呼ばれる。 HST固有運動 Kallivayalil et al. 2006a,b は HST の2時期データから LMC 26 領域の 固有運動を求めた。その内 12 領域に対してはさらに第3観測が行われ、 Kallivayalil et al. 2013 は計 7 年間の時間巾観測に基づいた固有運動を 与えた。その median percoordinate uncertainty は 0.03mad/yr = 7 km/s で ある。 マゼラン雲の公転運動 HST 固有運動はマゼラン雲の銀河系を巡る運動が、以前想定されていた よりも大きいことを示す。Besla et al 2007 はマゼラン雲の銀河系への現在 の接近は、両者の初遭遇であると述べている。これはマゼラン雲不規則銀河の 形成に関して重要な情報 Besla et al 2012 である。 |
マゼラン雲の自転運動 van der Marel, Kallvayalil 2014 は HST PM の LMC 円盤表面での変化を 調べた。彼らは PM 回転曲線を測り、それが視線速度(LOS) 回転曲線と整合 することを示した。PM回転曲線はヒッパルコスデータのみから Kroupa, Bastian 1997 が 36 LMC 星と 11 SMC 星の観測に基づいて求めた。それらは Mv < -6.5, V = 9 - 12 の若くて明るい星である。TGAS には 29 LMC と 8 SMC 星が載っている。我々は Gaia データ庫から pygacs (http://github.com/Johannes-Sahlmann/pygacs) を用いてデータを入手した。 エラーの比較 ヒッパルコスの PM エラーは 数 mas/yr になるが、 TGAS PM エラーは メディアンで 0.15 mas/yr である。これは HST の Kallivayalil et al. 2013 エラーに匹敵する。今回の結果は HST をしのぐ精度ではないが、 HST と独立 な確認を与える意味がある。そこで、今回 Kallivayalil et al. 2013 と van der Marel, Kallvayalil 2014 と同じ方法で TGAS データを解析した。 |

|
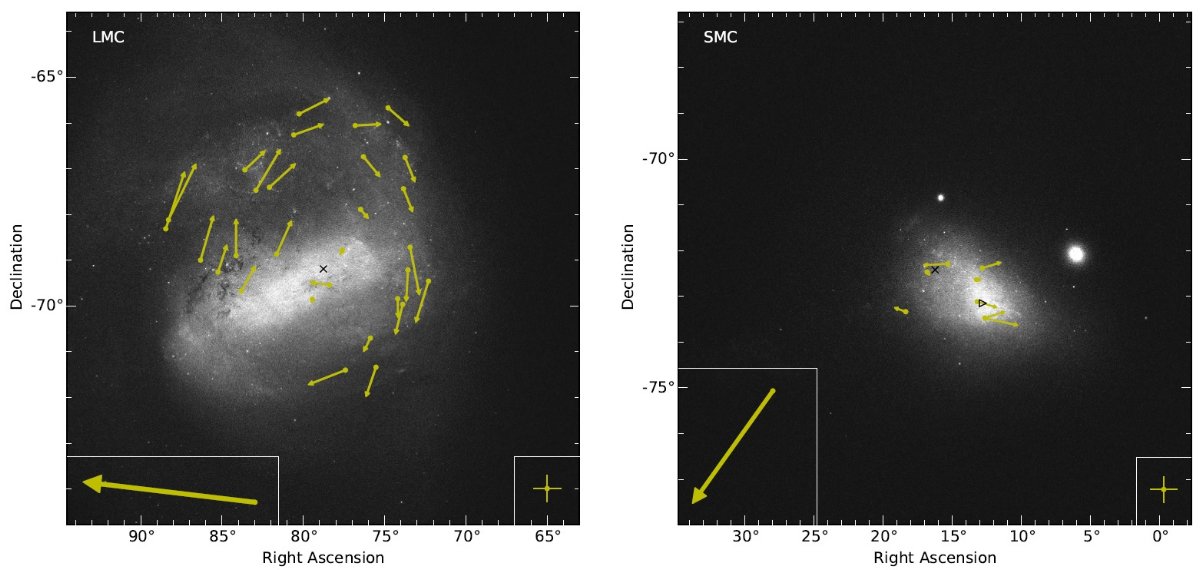
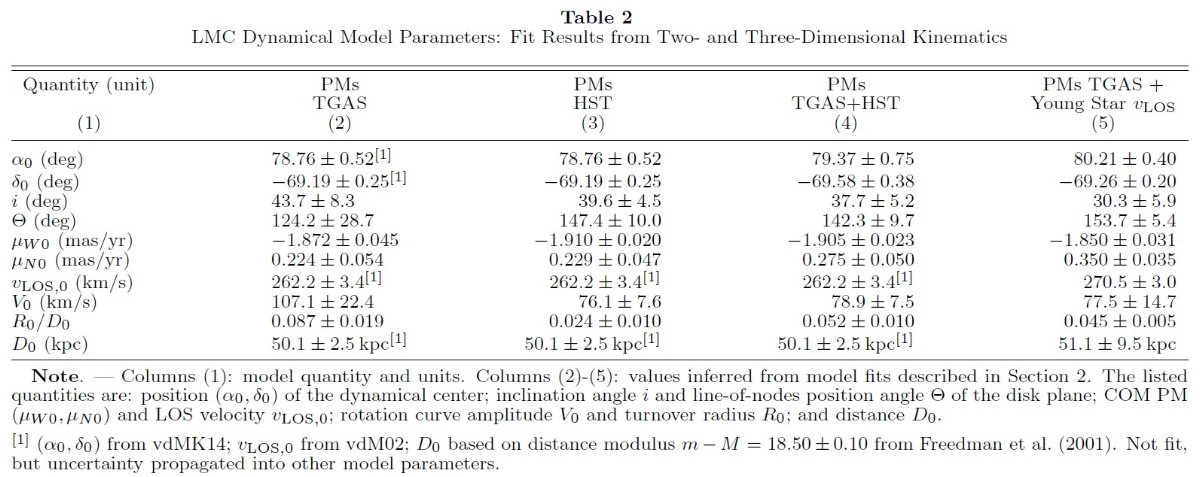
回転円盤モデル 図1a は LMC 固有運動場を示す。表1の各星毎に (PM) - (Com PM) を計算 した。時計回りの回転が認められる。我々は LMC が円回転する平坦な円盤と 仮定する。横断速度 vt(km/s), 固有運動 μ(mas/yr), 距離 D (kpc) の関係は, 大体 vt = 5×D×μ である。回転円盤の議論は van der Marel 2002 を見よ データ間の比較 表2にモデル化の結果を示す。第2列は新しい TGAS PM データのみを用いた。 LMC 南東側に LMC サンプル星が少ないため、LMC 重心運動はあまり良く決まら ない。そこでこのモデルでは、 COM PM は van der Marel, Kallvayalil 2014 の値を適用した。第3列は van der Marel, Kallvayalil 2014 から採った HST PM データを用いた。このデータは V = 16 - 24 の若い星と古い星の混成で ある。第4列は両者を合体させたデータにフィットした結果である。第5列 では、 van der Marel, Kallvayalil 2014 中の赤色超巨星 723 個の視線速度に TGAS 固有速度を合わせてフィットした。 (重みはどう配分?) 線形モデル 線形モデルは V = a R (R ≤ Ro) = Vo (Ro < R) と仮定して、 (a, Vo) を決める。我々はノンパラメトリックモデルを van der Marel, Kallvayalil 2014 と同じように求めた。図2の緑点は TGAS データをノンパラメトリックモデルで評価した結果、黒点はエラーを下げるた めに区間平均を取ってからのモデル化の結果である。 |
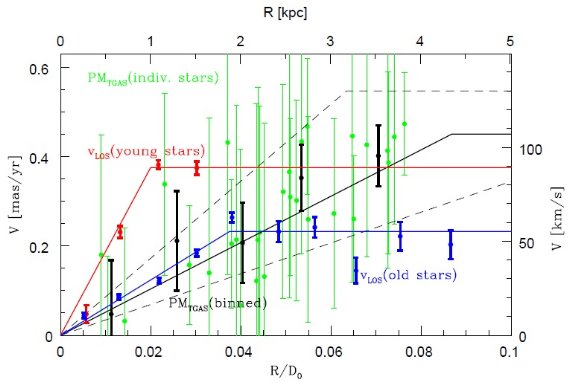 図2.LMC 円盤回転曲線。V(回転速度) - R(軸半径) 関係. 左軸は mas/yr, 下軸は R/Do 単位表示に注意。赤点=若い星の視線速度。青点=古い星の 視線速度。(van der Marel, Kallvayalil 2014 より)。緑点=TGAS 星固有運 動。黒点=ΔR=0.8 kpc 区分でのTGAS平均固有運動。 |
|
SMC 固有運動場 図1b は COM PM を引いた後の SMC 固有運動場を示す。明らかな回転運動 は見えない。これには二つの訳がある。第1に SMC は LMC より小さく TGAS 星が中心付近にあるため回転速度が小さい。第2に視線速度解析から分かった ように SMC は垂直方向に長く伸びていて、LMC より緩い回転を示す。 |
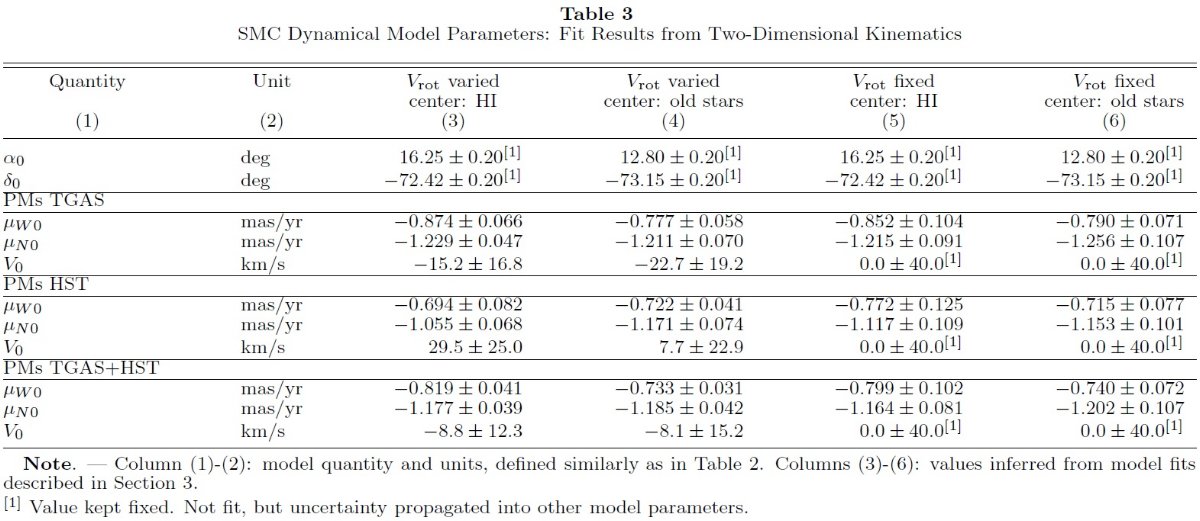
モデル 我々は SMC に対しては単純に全ての星が一定の回転速度 Vo を有する と仮定する。表3には SMC モデルのパラメタ―を載せた。 |
|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
