M31 の単純だが十分に正確なポテンシャルを作り、ハロー内での運動を
求めた。モデルには NFW ダークハロー、指数型円盤、Hernquist バルジ、中心
ブラックホールが含まれる。モデルパラメターは観測輝度分布、速度分散、
回転曲線からの制約により決めた。
このモデルは観測とよく合い、より細かなモデルとも一致する。ただし、ハロー
ポテンシャルは不確かで、また円盤とバルジの間には縮退が起きている。このため
パラメター空間内に広い、殆ど2次元的な不確定領域が生じた。
この不確定性を減らすために、ハロー集中度、バリオンの割り合い、星の M/L 比などに理論的な制限を加え、パラメターが物理的に有意義なより狭い 領域を見出した。我々が提案する M31 の質量分布モデルは Mbulge = 3.2 × 1010Mo, Mdisk = 7.2 × 1010Mo, M200 = 7.1 × 1011Mo, で M/Lbulge, R = 3.9, M/Ldisk, R = 3.3 である。
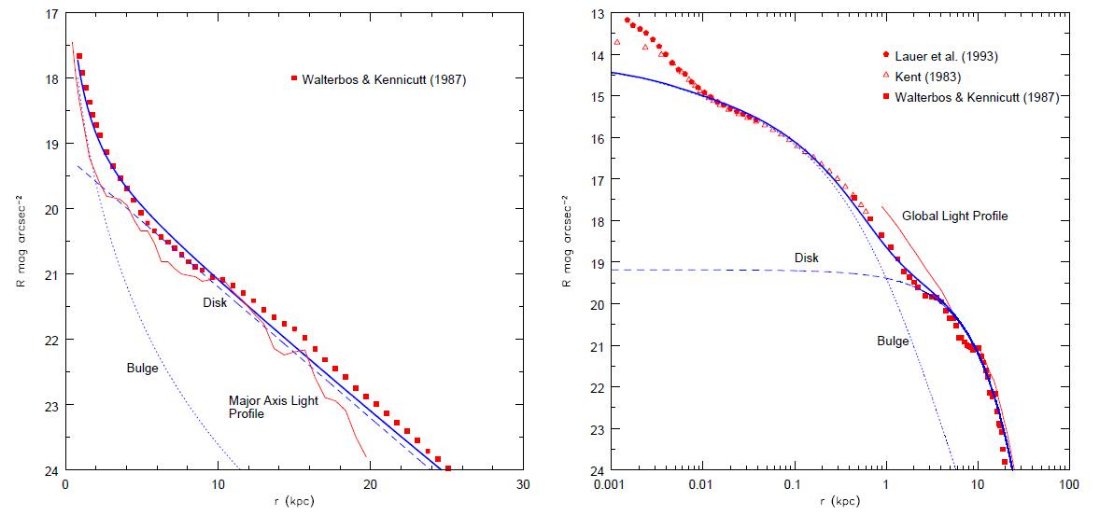
図1.(左)表面輝度分布。赤四角= Walterbos/Kennicutt 1987. 青線= ベストフィットライン。点線=バルジ。破線=円盤。実線=総計。
(右)内側の輝度分布。
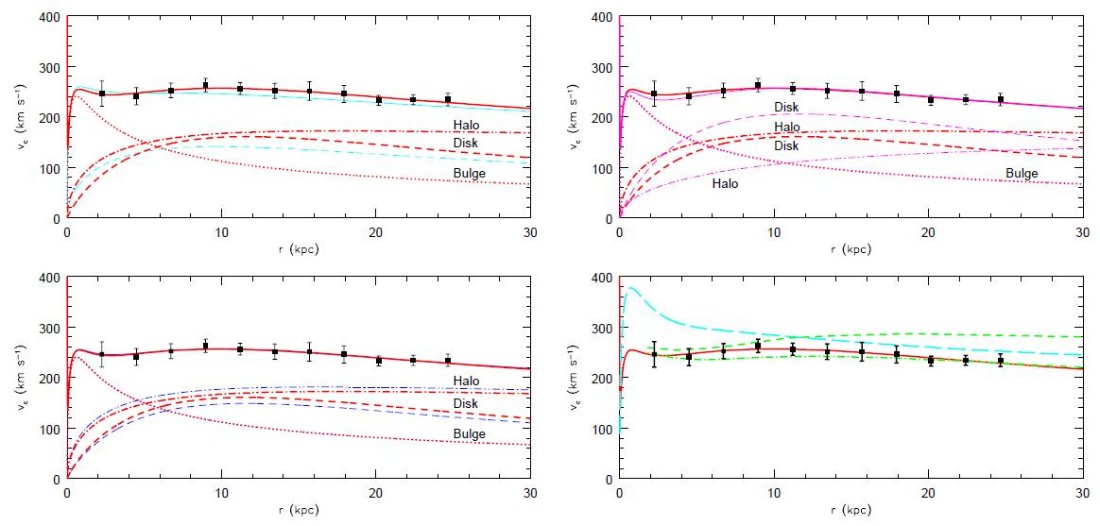
図2.(左上)赤線=軸対称円盤ベストフィット。シアン=球対称円盤モデルの場合。 R=0 のスパイクはブラックホールによる。
(左下)軸対称 constrained (M/L=3.3)円盤モデル(シアン)をベストフィッ ト(赤線)と比較。
(右上)maximum 円盤モデル(シアン)をベストフィット(赤線)と比較。
(右下)シアン長破線=Bekki 2001 モデル。緑短破線= Klypin,Zhao,Somerville 2002 の high model. 緑一点鎖線= Klypin,Zhao,Somerville 2002 の low model. と比較。
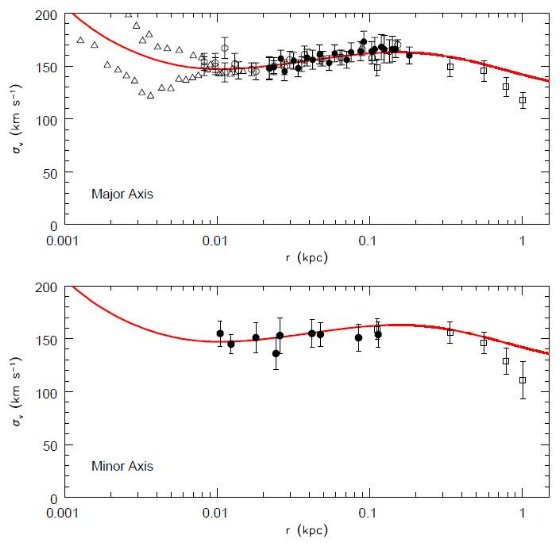
図3.(上)長軸沿いのバルジ星速度分散。(下)短軸沿いのバルジ星速度分散。 最内側の上昇はブラックホールの影響。
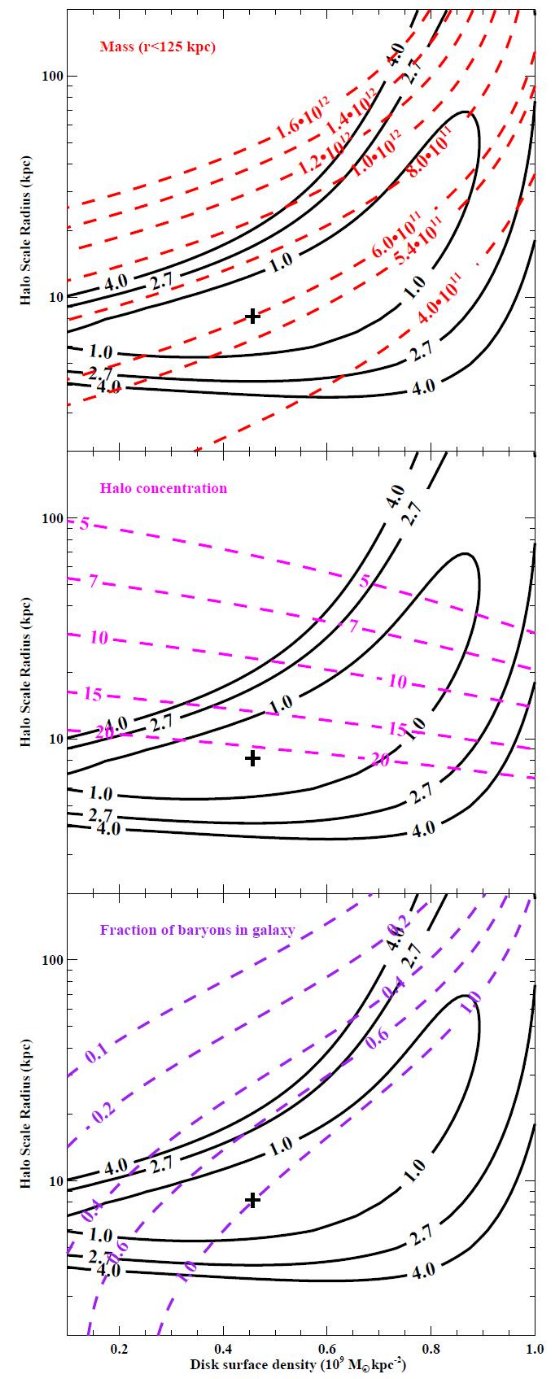
図5.黒実線=円盤表面密度とハロースケール長面での &Dleta;χ2 一定線。(上)赤破線=M(125 kpc) 一定。(中)ハロー集中度一定。 (下)バリオン比一定。 クロス=形式的なベストフィットパラメター。
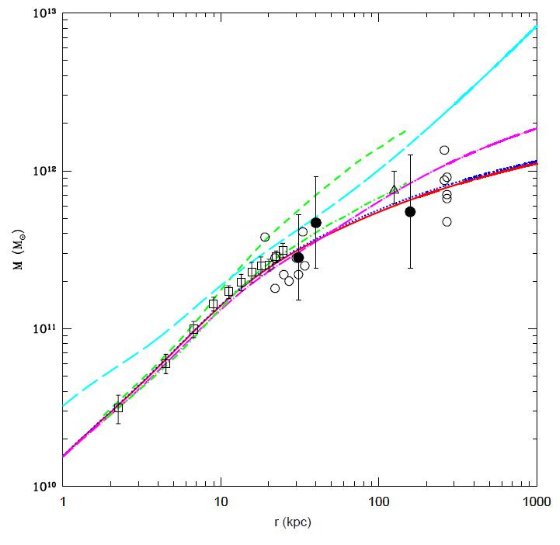
図4.質量プロファイルの比較。赤=ベストフィットモデル。青点線= (MR=3.3)でのベストフィット。マゼンタ一点破線=maximum disk のベストフィット。
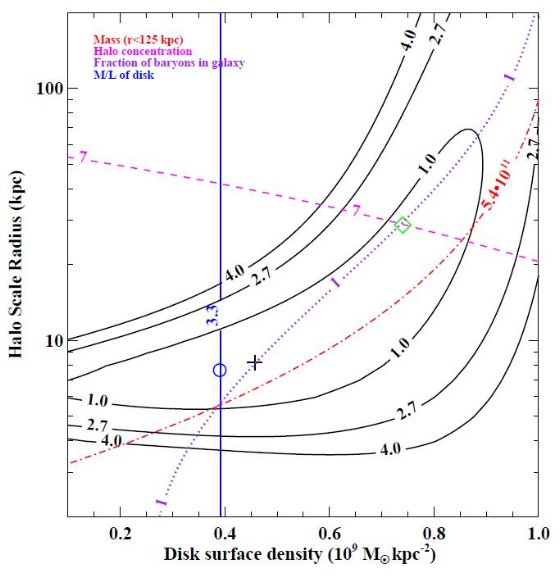
図6.図5から物理的に有意な領域、C200 = 7, fgal = 1, M(< 250 kpc) = 5.4 × 1011 Mo を選ぶ。それが丸印で (M/LR) = 3.3 ラインの上にある。
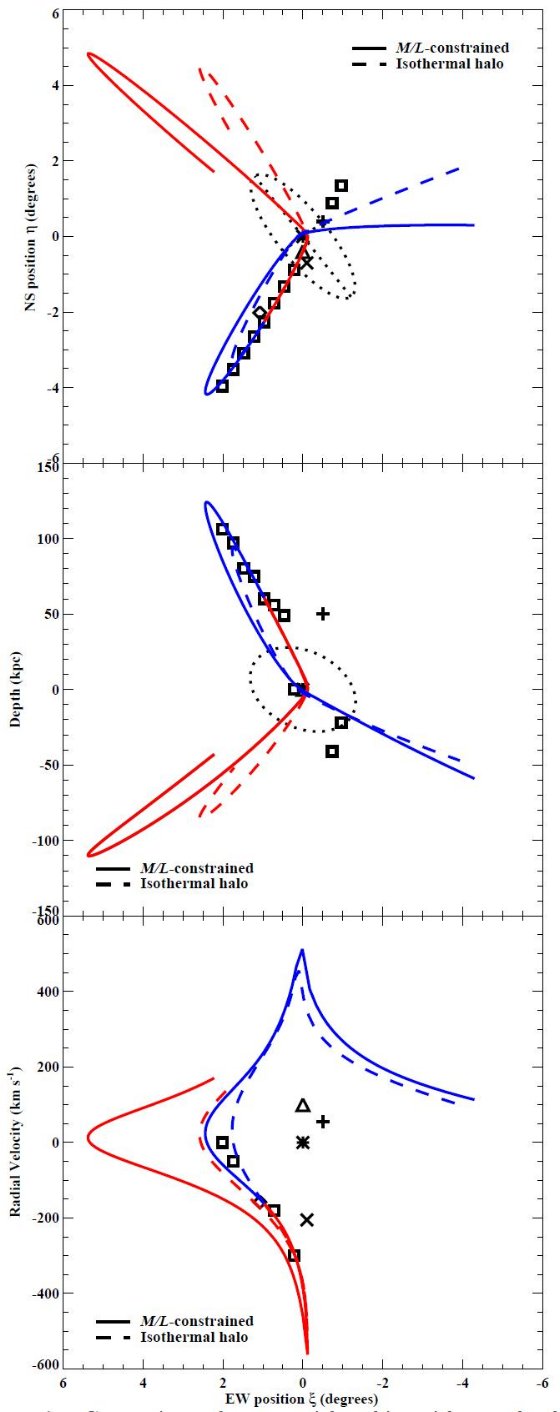
図7.モデルによる軌道の変化。