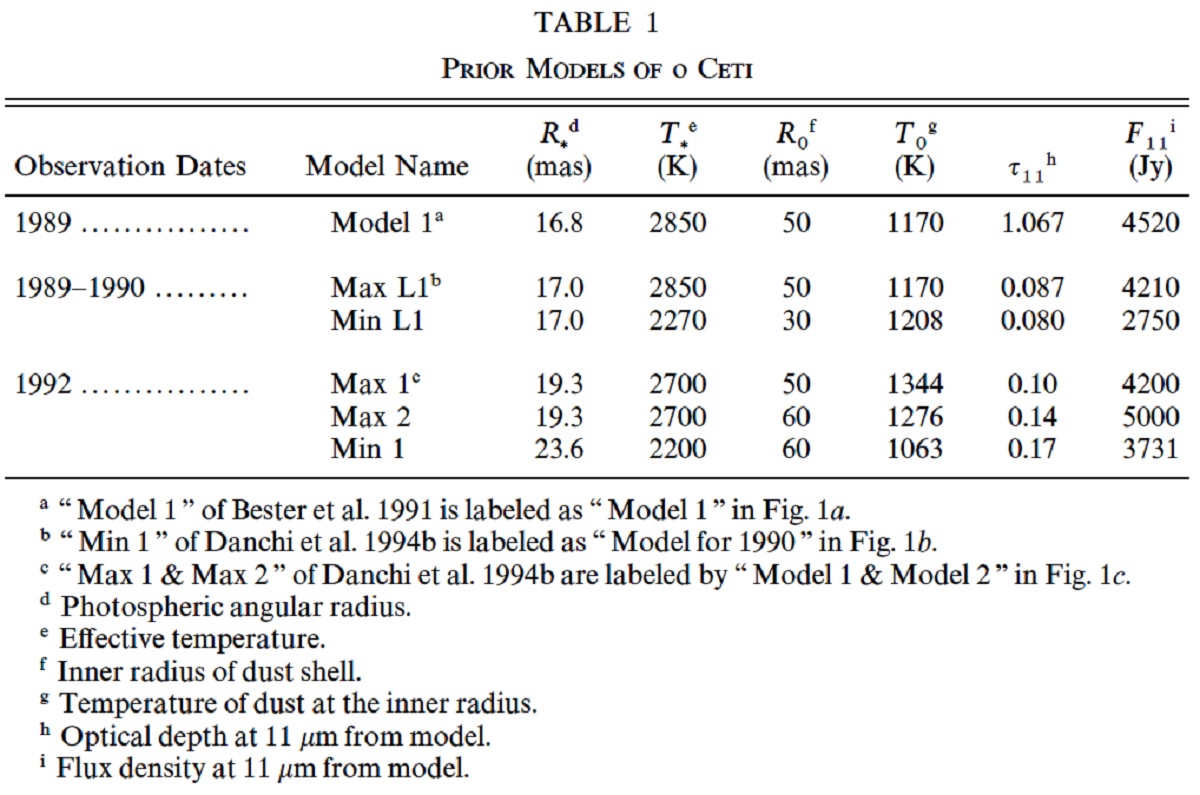
| 1988 - 1995 年に UC Berkley 赤外干渉計 (ISI) により ο Ceti の観測が 行われた。観測されたビジビリティは観測時により大きく変わり、位相による 光度変化でダストが暖められたり冷やされたりするという単純な図式に当ては まらない。その代わり、 ο Ceti の光球から数恒星半径内のダスト 密度が激しく時間変化していた。二つのダストシェル、一つは光球から3恒星 半径以内、もう一つは星から約10恒星半径、というモデルが観測をうまく説 明する。 | 4種類の軸対称な輻射輸達モデルをも、データと比べた。それらは、 (1)球対称なシェルの内側に楕円体空洞、(2)円盤、(3)一つか二つの 固まりをつけた球対称シェル、(4)相互に等間隔な薄い不完全シェルの群れ、 である。ビジビリティの時間変化を説明するため、全てのモデルには星光球に近い 距離でのダスト密度の時間変化が必要である。軸対称モデルは、球対称モデルの 距離に対応するところに、塊を持つ。観測された広帯スペクトルとの良い一致が これらのモデルで得られた。 |
| 中間赤外の長基線干渉計はようやくLPV観測成果が出版される水準にまで達 した。Danchi et al 1994 は 13 星の観測結果を発表した。αOri や IRC+10216、οCet の長期モニターも公表されている。 | ここでは οCet の 1988 - 1995 に行われた長期モニターの結果を 解析する。ビジビリティの変化は光度変化では説明できない。光球近くで起き るダスト密度の大きな変動が必要である。さらに、どのモデルでも、一様な質 量流出に代わって、相互に分離した離散シェル、円盤、塊などを必要とする。 |

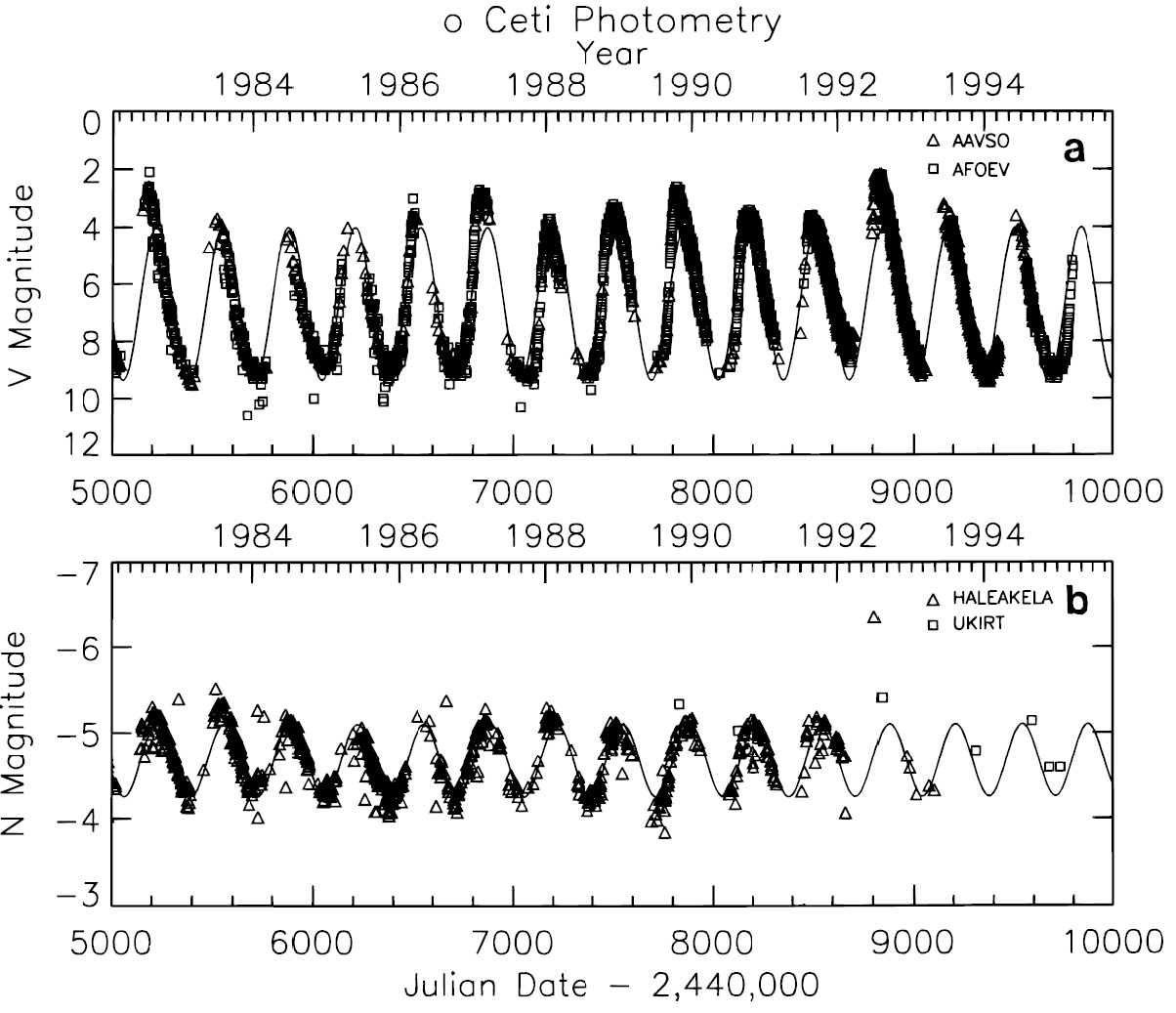
2.1.ビジビリティの測定表1=これまでISI による οCet 観測は過去 7 年間続けられた。Danchi et al 1994 はビジビリティ曲線を球対称輻射輸達モデルで解釈した。密度分布は r 逆二乗 とした。ダスト加速をモデル化した密度分布も調べられた。それらの結果は 表1にまとめた。 1989 - 1990 データ 図1(a) のビジビリティ変化は Bester et al 1991 が調べた。 1989 年極大(表1の"Model 1")と 1990 年極小(表1の "Min 1") は οCeti のモデルは、ダスト形成が観測されたビジビリティ変化を説明するのに良く合って いることを示す。極小期のシェル内側半径 0.03" から極大期のシェル内側半径 0.05" への変化は、極小期に余分のダストが形成されることを意味する。 1992 データ 新しい 1992 年データは上の解釈が不十分であることを示す。実際、 1989 年 10 月 10 日(φ=0.94) から 1989 年 12 月 5 日(φ=0.11) にかけてのデータと 1992 年 7 月 15 日(φ=0.98) から 1992 年 8 月 15 日(φ=0.08) にかけてのデータとの間には大きな差が存在する。両者は ほぼ同じ変光位相でのデータだが、1992 年データは明らかに恒星近傍で密度 増加が起きたという解釈に合う。 1993, 1994 年データ 図2にはその後 1993, 1994 年のビジビリティを示す。二つの極大期データ の間には大きな変化が認められない。それ以前のビジビリティとの差は、 (1)新しいビジビリティには空間周波数 7 105 rad-1 にコブがある。興味深いのは 1990 年極小期にも同じ位置にコブが見られるこ とである。 (2)1993, 1994 年極大期のビジビリティは 1989 年極大のビジビリティと 同じである。 (3)1992 年データは他と異なる。この年の極大が異常に高かったこととも 考え合わせると、何か異常な出来事があったのではないかと思われる。 2.2.測光異常極大1988 - 1994 の観測期間中周期は長い時で 353 日、短い時は 306 日であった。 1992 年の極大はその前後よりずっと明るかった。 1835 年の AAVSO 開設以来 1992 年のように明るい極大は何回か起きている。発生に規則性はないが、 典型的には 3 - 5 周期ごとに振幅は大きくなる。実は 1989 年も高い極大 だったのだが、 1992 年ほどでなかった。 赤外モニタリング 図4(b) は Maui Surveillance Site (MSSS) と UKIRT での N バンド 測光モニタリングを示す。サインカーブフィットの赤外極大は可視極大に 46 日遅れる。しかし、可視の変光曲線の極大はサインカーブより 31 日手前に なるから、実際にはその差は 77 日である。この赤外ピークの遅れは、 Lockwood, Wing 1971 が見出した 0.1周期の遅れと一致する。 赤外 SED UKIRT では 1989 年から中間赤外観測が続いている。図5の赤外スペクトル は 7 - 9 μm に大気 SiO の吸収バンド、 9-12 μm に星周ダストの放射が 見える。 (7-9μm では星の放射が支配的な のか?どこで切り替わるのか? ) |
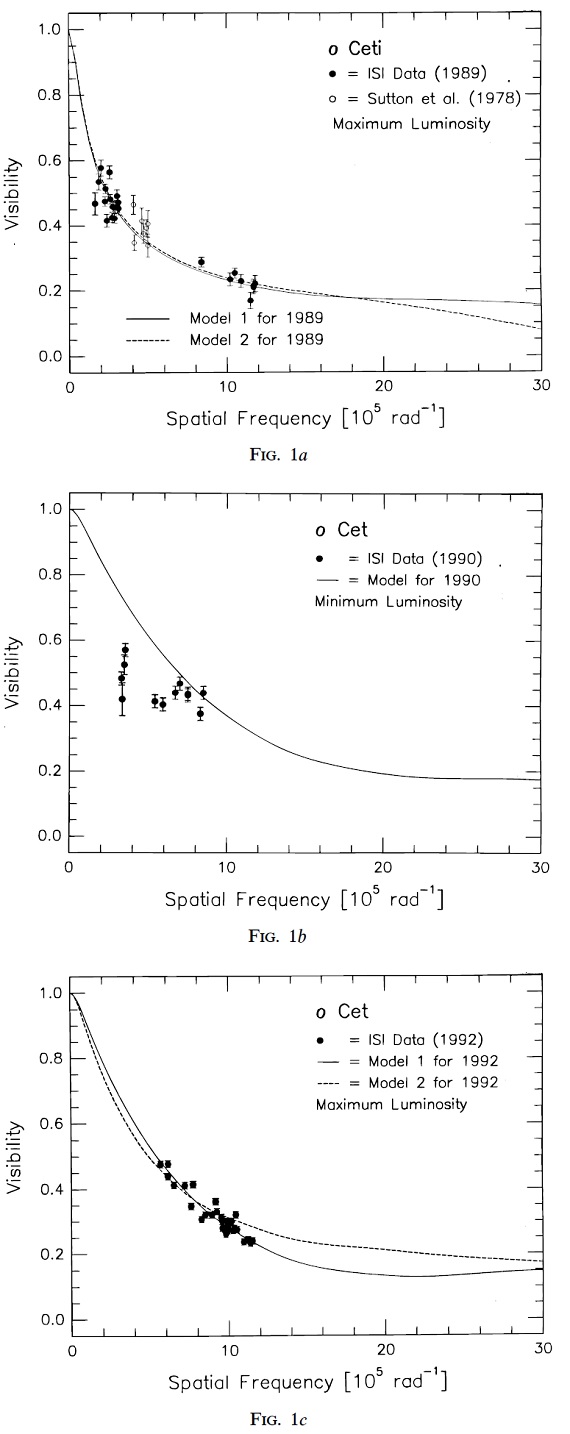 図1.οCet のビジビリティデータとモデル曲線。 (a) 1978, 1989 年極大期。Bester et al 1991。 (b) 1990 年極小期。Danchi et al 1994。 (c) 1992 年極大期。Danchi et al 1994。1989 極大と 6 105/rad に大きな差があることに注意 |
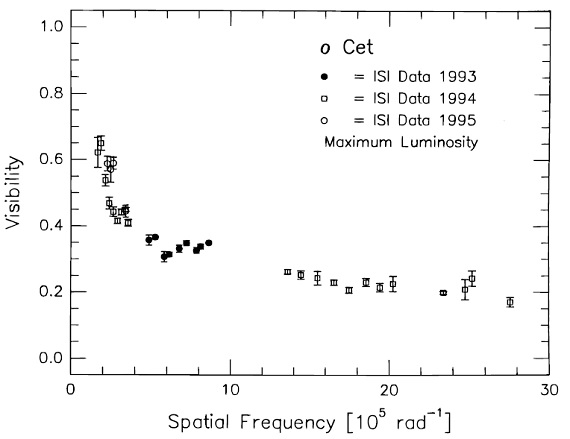 図2.1993, 1994 年極大期近くでのビジビリティデータ。 このデータと 1992 年極大期との差、1989 年極大期との類似に注意。 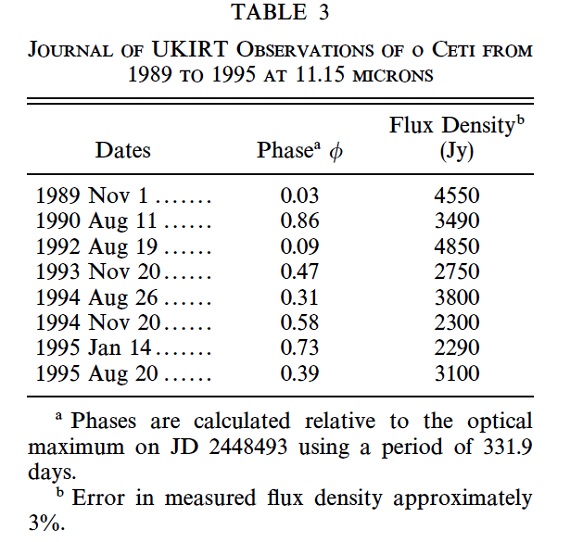 表3.UKIRT 観測ログ |
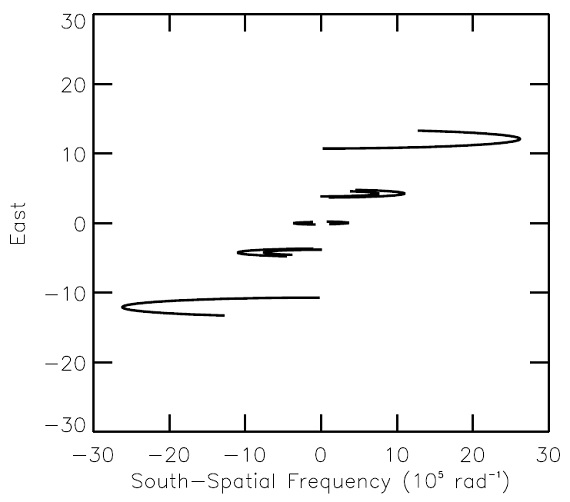 図3.ISI のフーリエ(u,v)面。原点に近い方から基線長 4, 9.6, 13, 32 m. (でも(u,v)を知らないから、これが一回の 観測なのかどうかも分からない。) 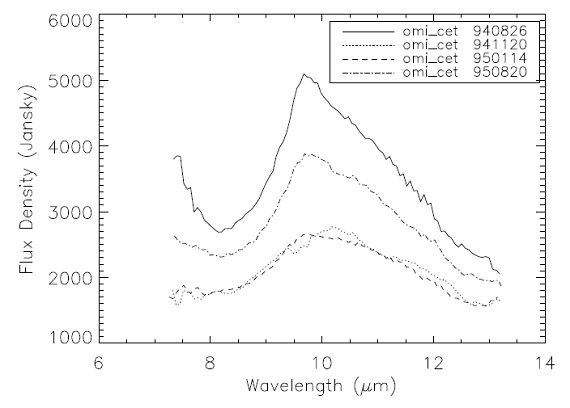 図5.οCet の赤外スペクトル。 |
|
0.7 μm Karovska et al 1991 はスペックルに一様楕円をフィットして、位置角 115°, 軸比 0.85, 主軸長 68 mas を得た。 Wikson et al 1992 はガウス 楕円をフィットして、位置角 120°, 主軸長 30 mas 、軸比 0.85 を得た。 Haniff et al 1992 もまた一様楕円から 位置角 119°, 主軸長 55 mas 、 軸比 0.82 を得た。 この形が星本体由来と考えられているが、ホットスポット の存在や、非対称分布ダストからの散乱という説明も可能である。 ホットスポット Tuthill 1994 はミラのホットスポットをアパーチャマスキング法で観測した。 1−3個の高温域が異なる時期のデータを説明するために必要である。 対照的な楕円モデルより、円盤+点のような非対称配置の方が適当である。 |
散乱光 ダスト高密度域からの散乱光もまた見かけの形を変える。ダストの空間分布 が一様でないことは十分に考えられる。分解能 6" の CO(J=2-1) 観測から、 Planenas et al 1990 は星から 3" 北に青方変移した放射を 3" 南に赤方変移 した放射を見出した。これは星風が赤道に存在する高密度ガスに部分的な衝突 を起こした結果の非常に遅い双極流ではないかと解釈された。 TiO 放射 Haniff et al 1992 は TiO 放射ー連続光をマップ化して、大気の形が非対称 であることを見出した。TiO 放射光は星中心から 35 mas 離れ、位置角 113° の弧を描いている。位置角 320° の方向には小さな斑点が見える。弧の 位置角は伴星 ミラB の方向に一致する。TiO 放射マップに対しては、 ミラB の EUV光がミラ大気の片側を照らす、ミラの外側大気の非対称性、 ダストの非一様分布の効果など色々ある。 |
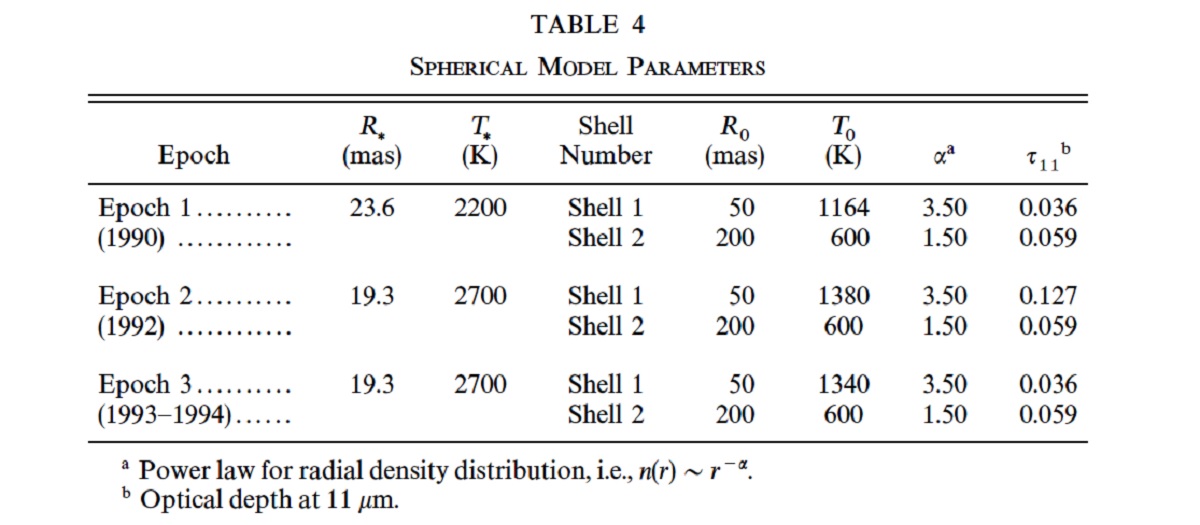
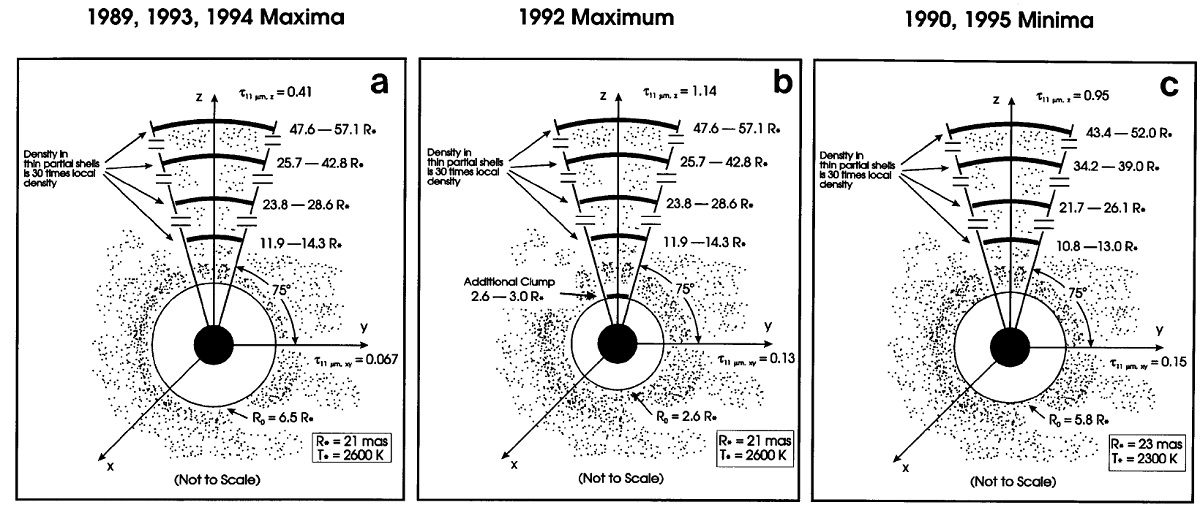
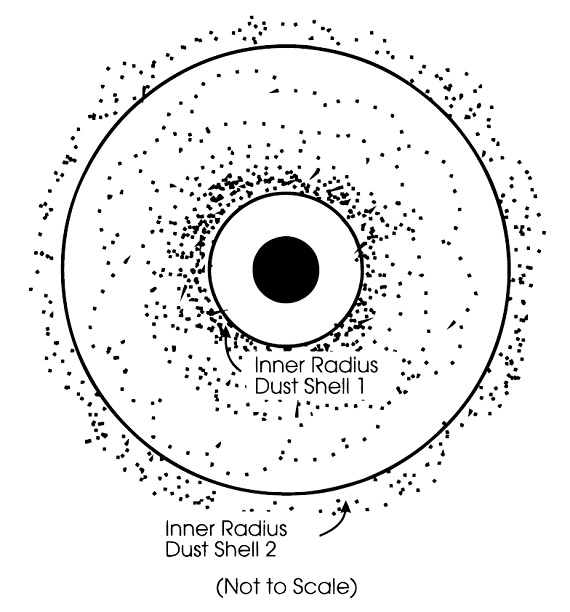 図6.ο Ceti ダストシェルの漫画。距離 50 mas = 3 Rs と距離 200 mas = 12 Rs にある二つのシェルから成る。 単純シェル ρ ∝ R-α (R>Ri) の単純な一層シェル は図1,2に示される変化を説明するのに用いられた。それは星の光度変化に 伴って、Ri が変化するものである。しかし、このモデルでは 1990 年から 1992 年にかけての変化、特に空間周波数 7 105 rad-1 以下の周波数帯を説明できない。1992 年のフィットではモデルビジビリティが データよりかなり高い。これはモデル 1992 極大期モデルが 1990 年極小に 比べ、星近傍でより強くダスト放射させていることを意味する。しかし、 1989, 1993-1994 年のデータは 1992 年データより下になる。つまり、 1992 極大期には他の極大期よりもずっと多くのダスト放射が星近傍から出ていた ことを意味する。 ダブルシェル 今回の計算では R = [Ri, Ro] でべき乗則密度分布を仮定する。多重シェル の場合は各シェルに同様の分布を与える。ダスト光学定数は Draine, Lee (1984), Draine, Lee (1987) から採った。グレイン半径は Mathis et al 1977 の n(a) &sim: a-3.5 を仮定した。光の波長は ライマン端から 1000 μm までの 47 波長を選んだ。 採用したダブルシェルは図6に示すように、数 Rs から始まる第1シェルと、 約 10 Rs からの第2シェルとから成る。計算されたビジビリティを図7に示す。 そのパラメターは表4に載せた。このモデルは最近の 1993 - 1994 年データを 合わせるために作られた。図7(c) がそれである。1992 年極大をこのモデルで 合わせるには、第1シェルの密度を 3.5 倍に上げる必要があった。それを図7 (b) に示す。その結果光学的深さは約2倍になった。1990 年極小は図7(c) モデルと同じ密度分布であるが、星光度を半分にした。 ダブルシェルのフィットが上がった理由は、第一シェルダストが星近くでの 11 μm 輝度を高めたからである。 |
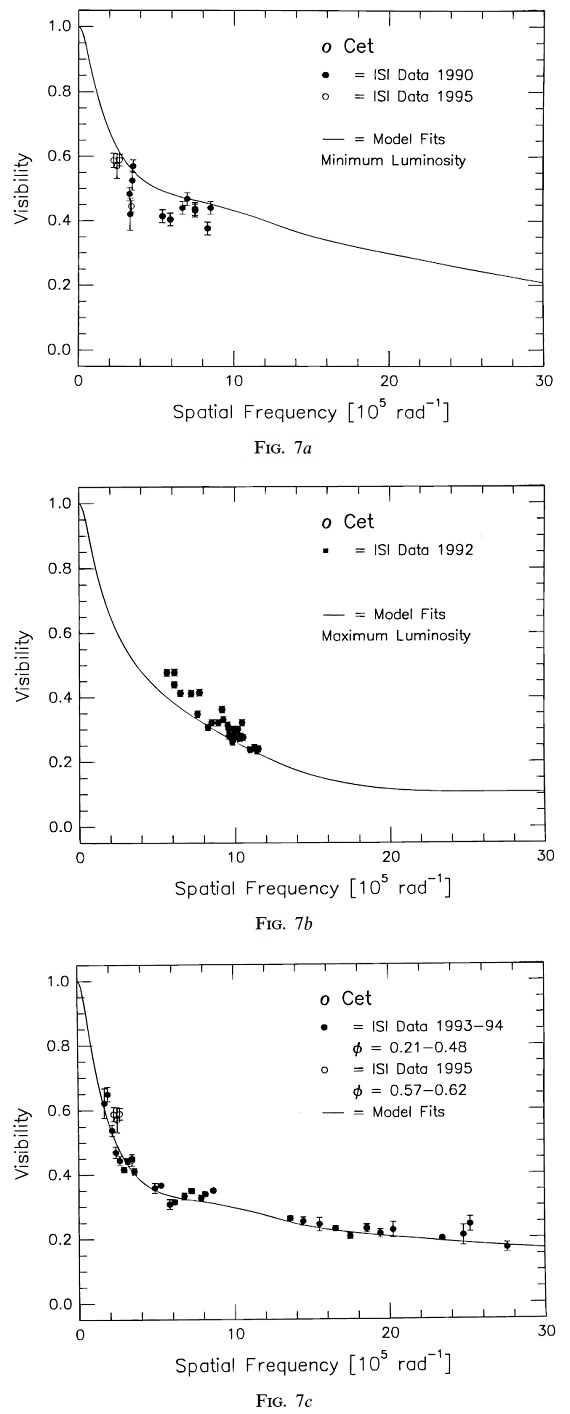 図7.観測ビジビリティ。 (a) 極小。黒三角=1990, 白三角=1995. 実線=表4のエポック1モデル。 (b) 極大。黒丸=1992. 実線=表4のエポック2モデル。 (c) 1993, 1994 (φ=0.21-0.48), 1995 データ(φ=0.57-0.62)。 実線=表4のエポック3モデル。 |
|
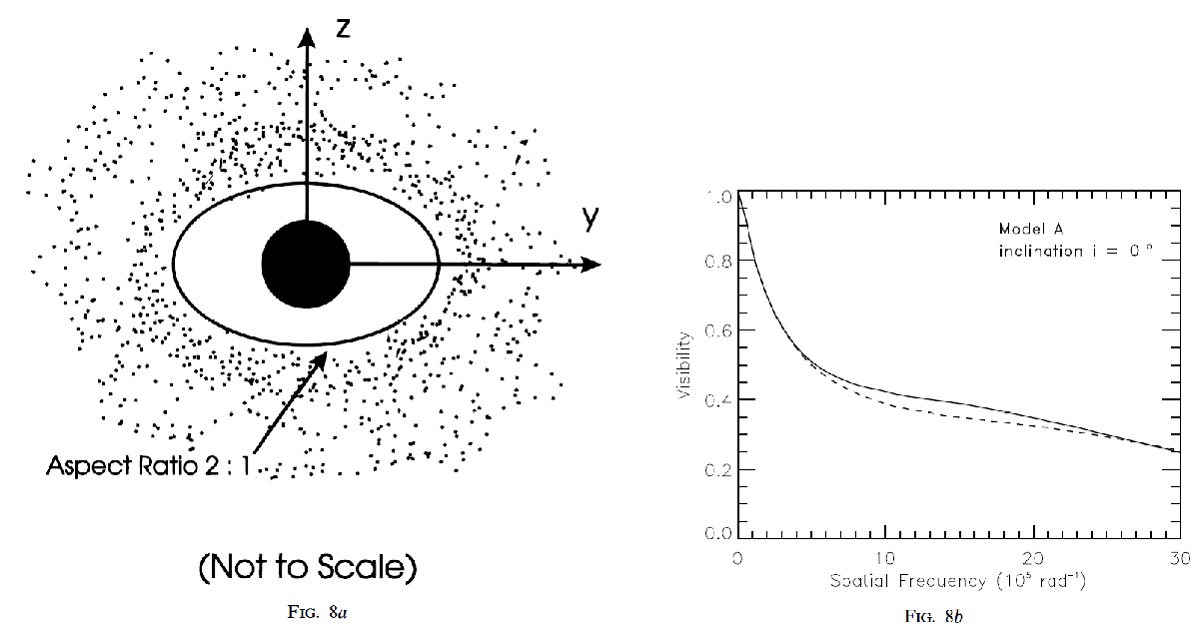
軸対称性 軸対称モデルを30波長のモンテカルロ計算で扱う。軸対称シェルは400 個の円環から構成され、各円環は等温とする。 5.1.回転楕円体空洞モデル空洞の形密度の動径方向分布 ∝ r-1.5 と仮定する。この分布が FIR SED の再現に適当だからである。星温度 Ts = 2700 K. ダスト半径 0.1 μm. モデルA 軸比2のプロレイト空洞。短軸半径= 2.5 Rs. 長軸半径= 5 Rs. モデルB 軸比2のオブレイト空洞。短軸半径= 2.5 Rs. 長軸半径= 5 Rs. 光学的厚さは短軸方向で 0.14, 長軸方向で 0.1 である。波長は書いていないが 多分 11 μm での値。 結果 図7(b) にモデルAに対して、短軸、長軸2方向からのビジビリティを示す。 面白いことに両者に大きな違いはない。同じことはモデルBについても言える。 これは、空洞の非球対称性は 1992 年に見られた異常性の説明に適していない ことを示唆する。その理由は、シェルの広い領域が 11 μm 放射に寄与して いるからであろう。 |
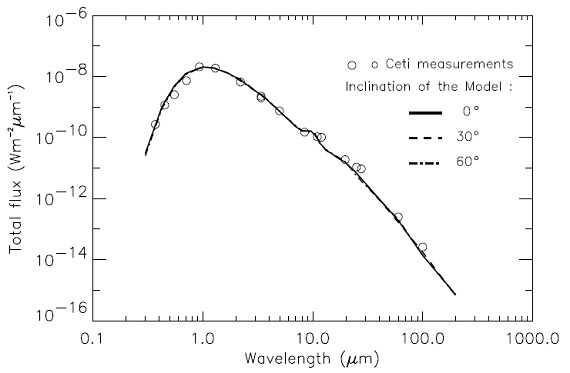 図9.ο Ceti のSED.丸=かんそく。モデルは Rowan-Robinson, Harris 1983 の極大時データへのフィット。 |
|
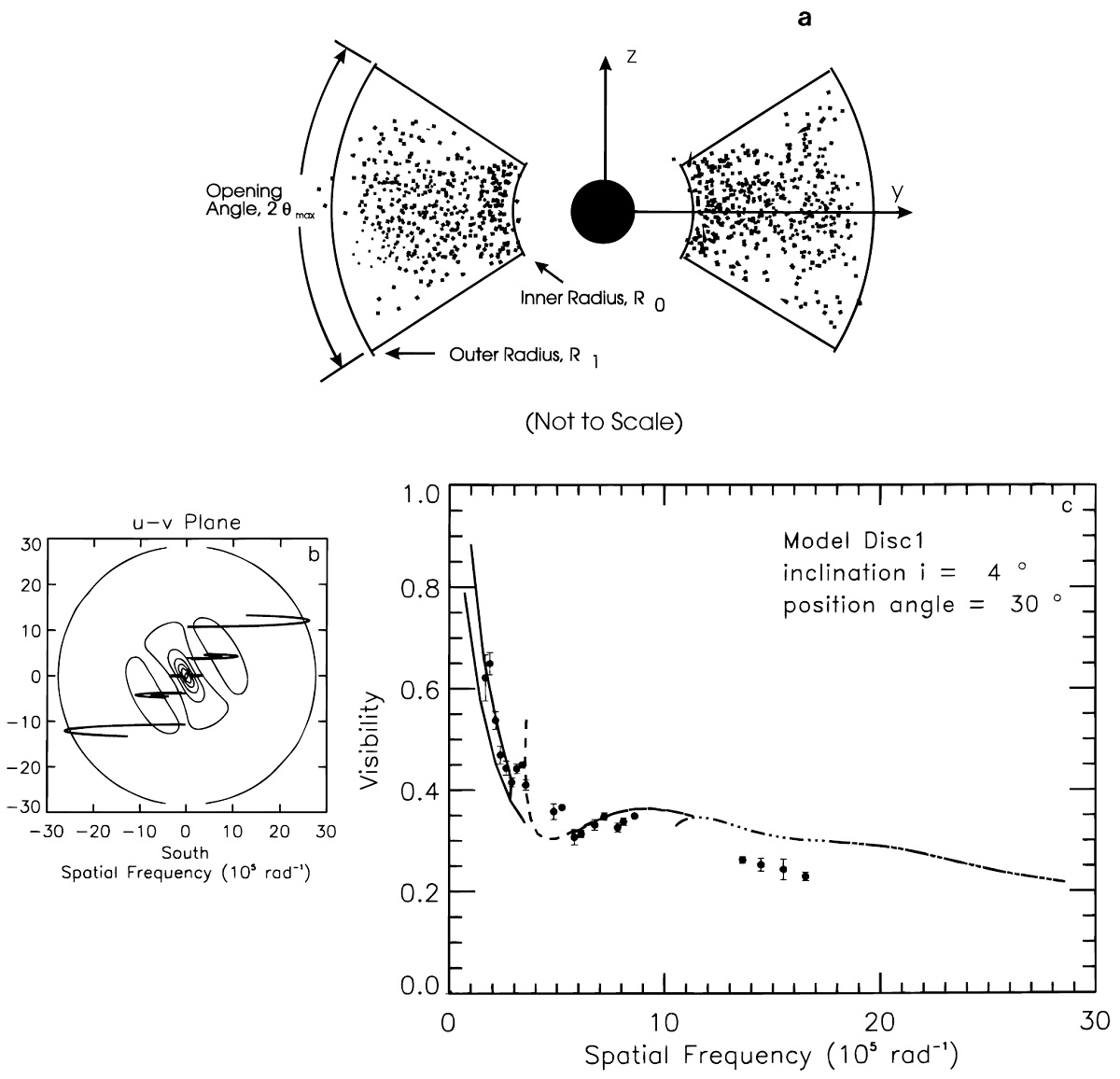
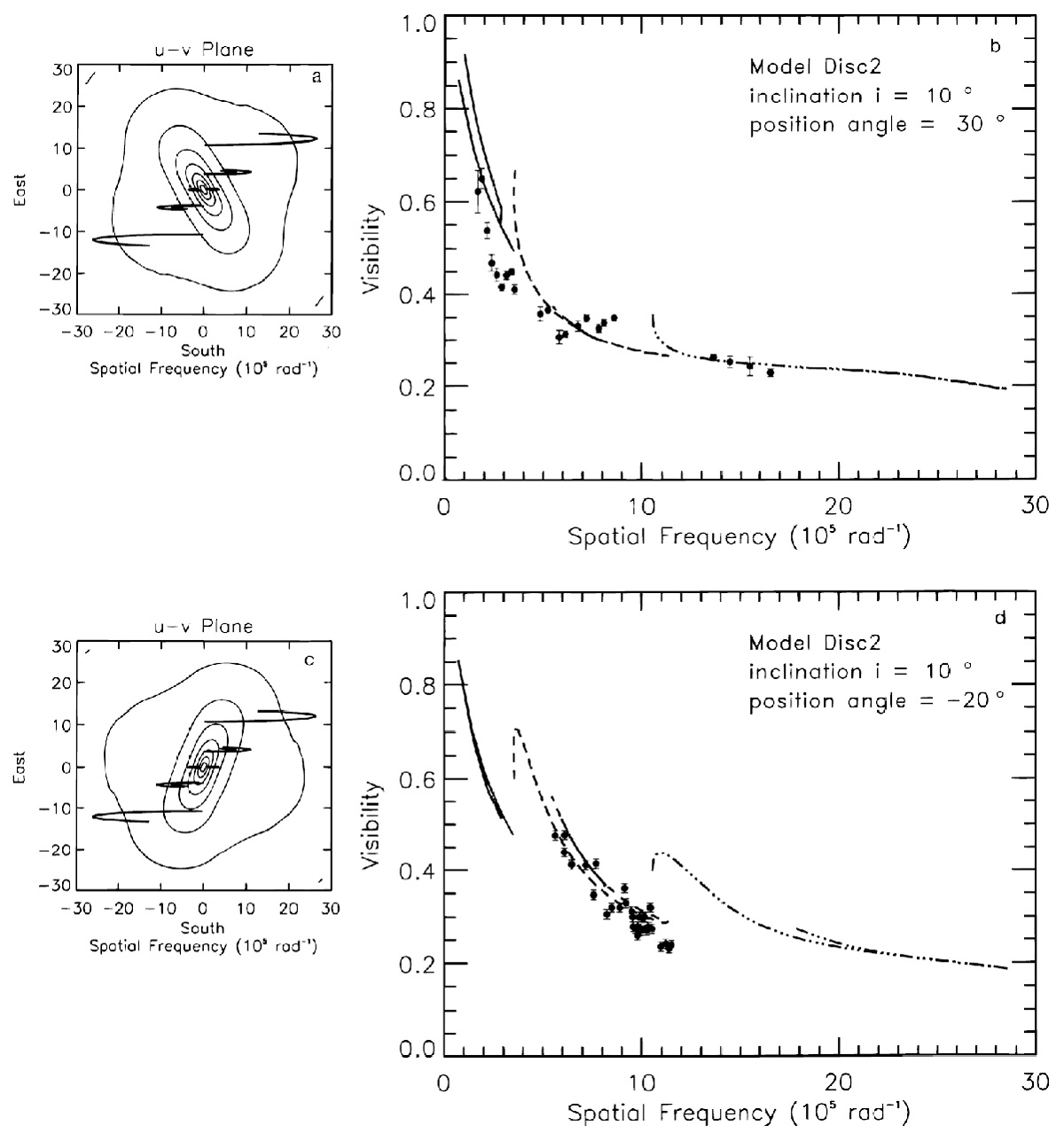
AGB星の軸対称構造 post-AGB 星の大部分には軸対称構造が見られる (Bujarrabal et al 1992, Meixner 1993) 。AGB 星の円盤のはっきりした証拠はないが、Planesas et al 1990 のミラCO観測は二つのローブを検出した。このローブは星の赤道面 上の高密度域により星風が部分的に整流化したものと解釈される。。 円盤モデル n(r,θ) = f(r)g(θ), ここに θ = 円盤面からの緯度。 f(r) = r-1.5, g(θ)=1+cos(θ×180°/40°) とする。ただし、θ>40° で g(θ) = 0 である。Ts = 2800 K, ダスト半径 a = 0.1 μm とする。星の角半径 19 mas である。 円盤モデル1 ダストの存在は [10, 800]Rs、τ11 = 0.09. モデル1の ビジビリティマップと ISI 観測の軌跡を図10(b) に示す。1993-1994 年 データに最も良く合うのは, 円盤が視線に対する傾き角 4.5° の時 である。観測ビジビリティに見られる (7-8)106 rad-1 にあるコブはこのモデルで再現された。 |
モデル2 内端半径が小さくなり Ri = 3 Rs, τ11 = 0.12. この モデルは 1993 - 1994 データを全体としてはモデル1より上手く説明する。しかし、 内端が近づき過ぎるため、コブが消えてしまう。図11 (a), (b) にその様子が 示されている。図11 (c, (d) には 1992 ビジビリティが位置角を動かしたモ デルで上手く説明されている。 パワースペクトル 図12には Karovska et al 1991 がミラに対して得たパワースペクトルを 円盤モデルで再現できることが示されている。彼らのデータは 1987 年 12 月 30 日から 1988 年 1 月 3 日にかけて撮られ、位相は 0.97 である。 モデルパワースペクトルの形は、短波長ほど細長くなり観測に合う。 円盤の利点と欠点 個々のモデルのフィットは良いのだが、位置角が大きく変化するのは非物理的 で問題である。 |
|
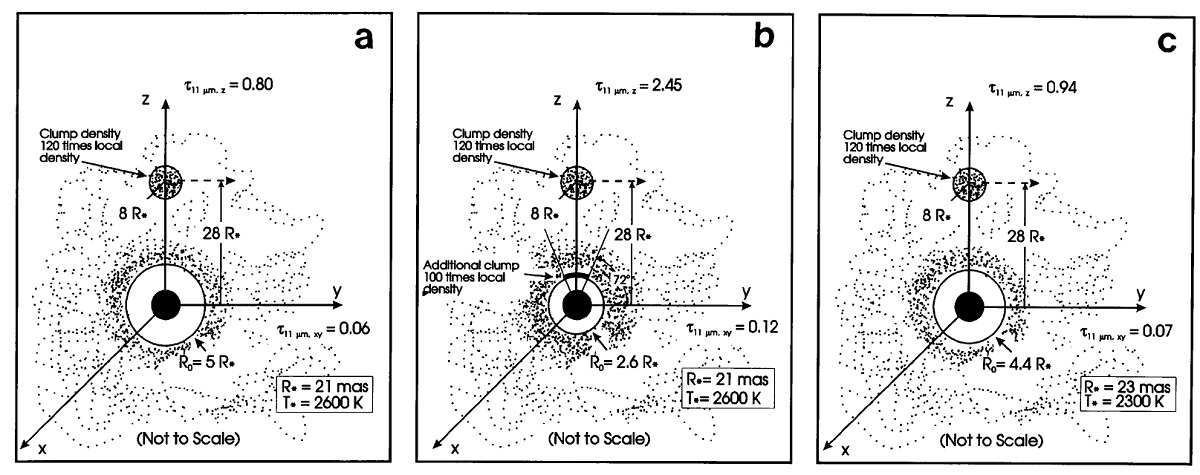
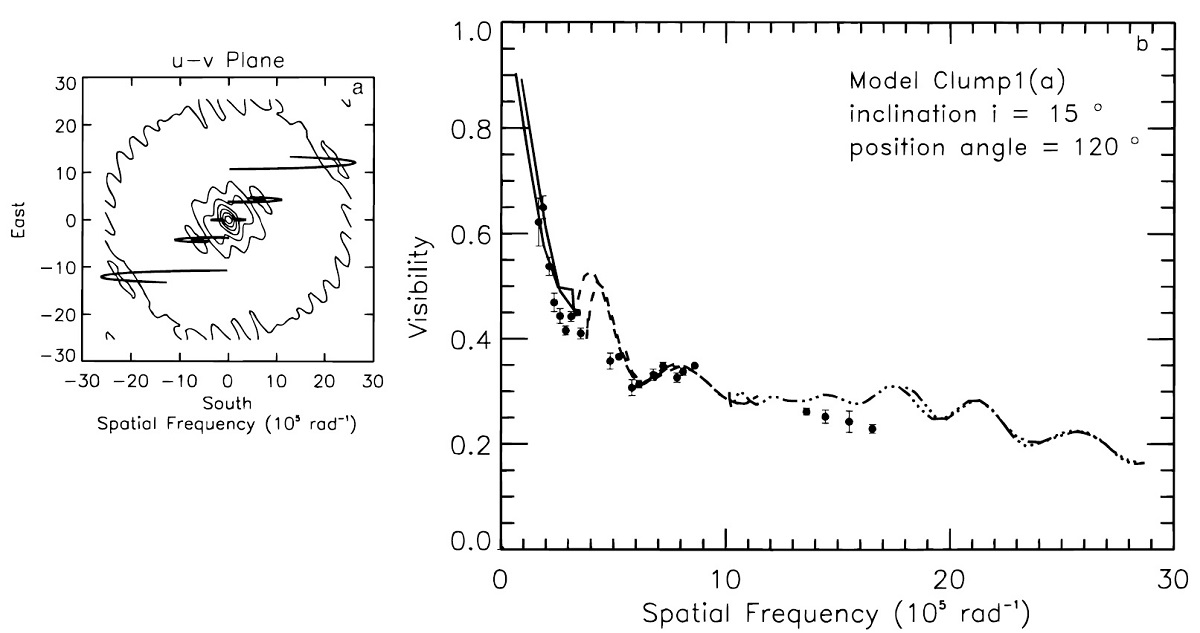
基底シェル ダスト塊は基底シェル中に埋もれている。基底シェルの内端はモデルにより、 2.6 Rs または 5 Rs である。 モデルクランプ1 最初のモデル系列はクランプ1と名付けられ、そのパラメターは図13に 示されている。クランプを通して見る光学的深さは 11 μm で 0.86 である。 図14にはクランプ1モデルのビジビリティを示すが、二重構造に由来する 数個のデコボコが見られる。最初のコブは 4 105 rad-1 に現れるが、そこでのデータが欠けているので真偽の確認ができない。 |
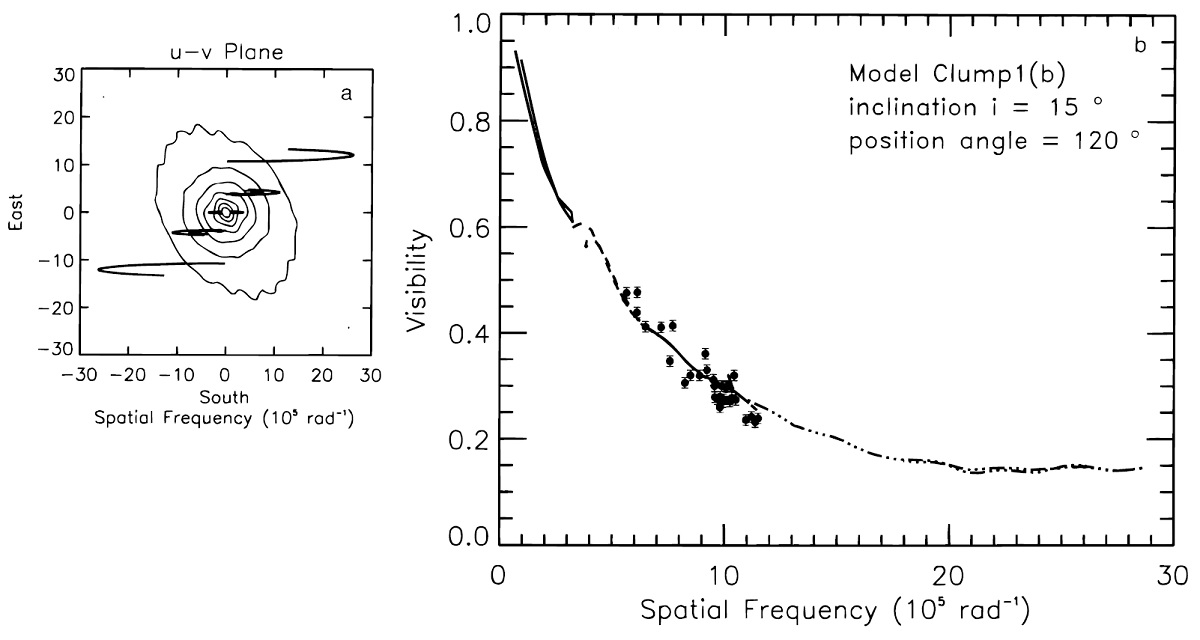
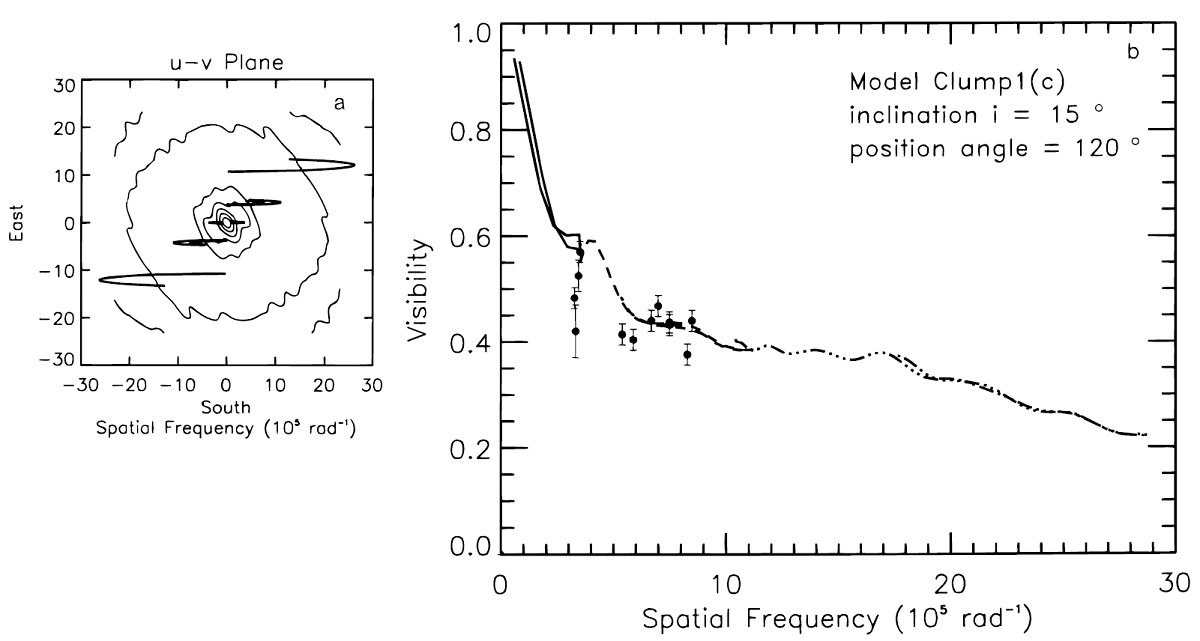
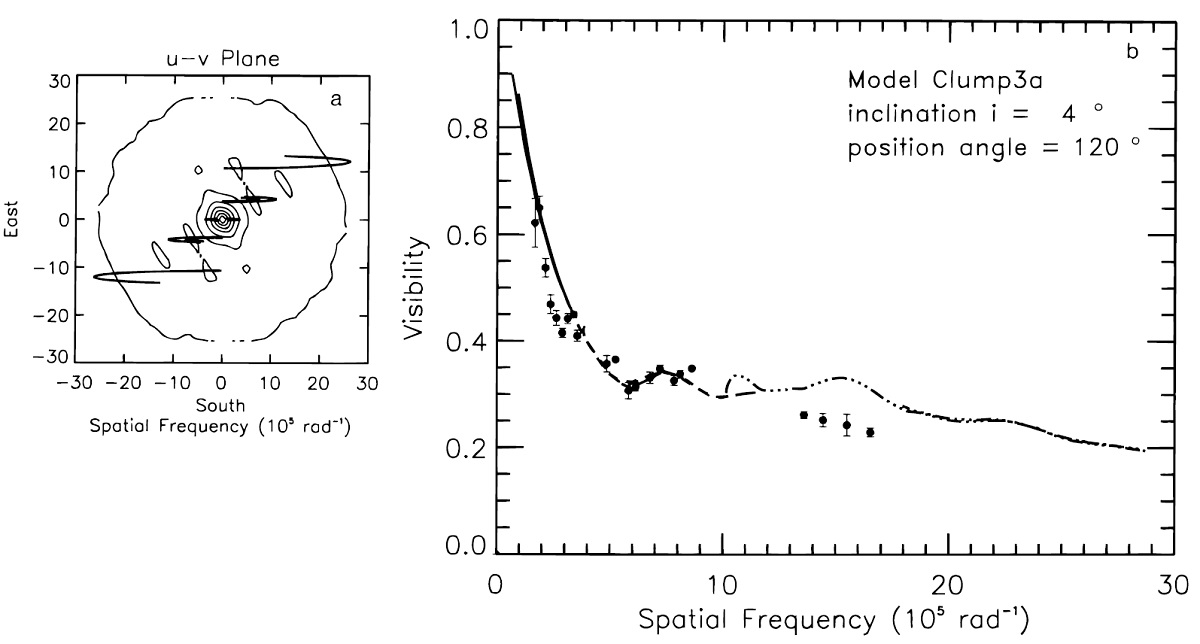
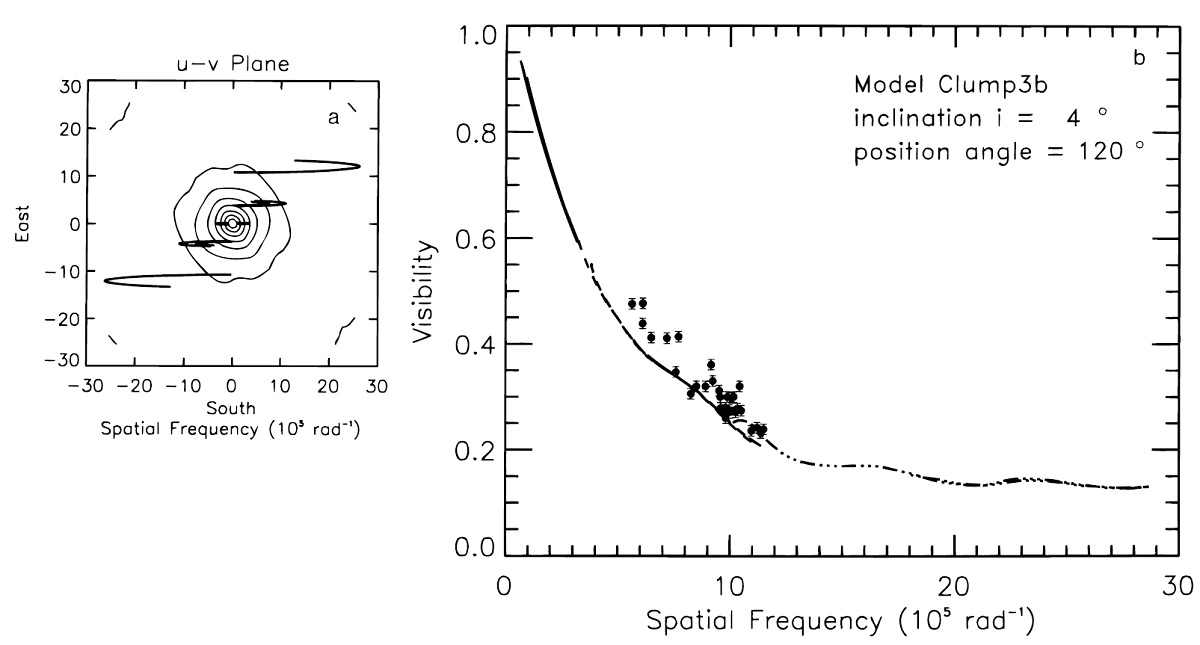
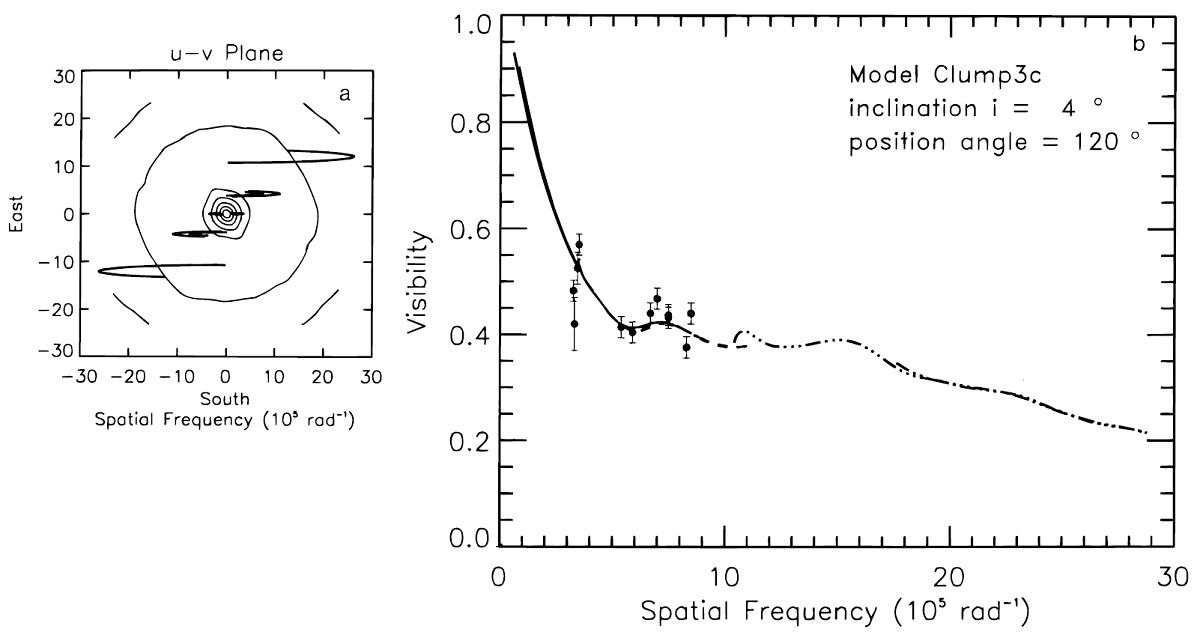
モデルクランプ2 モデルクランプ2はモデルクランプ1とほとんど同じである。これは モデルクランプ1を星に関して対称化したものである。z 軸方向の光学的深さは τ11 = 0.52 で, モデル1の 60 % 低い。現在の2望遠鏡観測 ではモデル1とモデル2のどちらが良いかは決められない。 モデルクランプ3 モデルクランプ3はシェルの数が増えている。これは周期的なダスト形成 事象の結果かも知れない。 |
|
伴星 Karovska rt al 1993 によると、Miraの伴星は, 距離 0".61, 位置角 112° である。その軌道周期は 400 年以上と長く、 ISI 観測期間中は位置が固定さ れていると考えてよい。 モデルクランプ1と伴星 モデルクランプ1では、二つのダスト塊それぞれの位置は 8 Rs と 28 Rs で、 クランプの間隔は 0".55 で、位置角は 120° である。伴星の位置角と、 近距離側ダスト塊の間に物理的な関連があるのかもしれない。 ダスト形成の多重周期性 Winters et al 1995 はダスト形成の動力学モデルを炭素星で計算した。 彼はダストが孤立した層として形成されることを示した。組成は違うが O-リッチでも定性的には当てはまると考えると、ダスト孤立層の形成は ビジビリティの時間変化を引き起こすと考えてよいだろう。 さらに、 Fleischer, Gauger, Seldmayer 1995 は脈動と独立に生じる不安定 性がダスト形成に周期性をもたらすことを見出した。この不安定性固有 周期と脈動周期との結合が変光とビジビリティに多重周期性を引き起こす だろう。(Winters et al 1995) CO の終端速度は 4 km/s であるから、ダストシェルの膨張は1変光周期当たり 1 Rs 以下である。クランプ 3 モデルで仮定された多重ダスト層は約 10 Rs 間隔で並んでいた。この間隔は脈動周期毎に発生したとするには広すぎるので、 ミラの周りのダストは多重周期性を以て形成されると考えられる。 |
ナンセ電波望遠鏡 ナンセ電波望遠鏡は 1990 年から OH メーザーのモニタリングを開始している。 その結果、1992 年に以下のような異常が見つかった。 (1) 1665 MHz 左手系円偏光の強度が 1992 年極大の2か月後に 2.5 倍に増加。 (2) 1992 年に赤方変位した 1665 MHz 成分が出現。この成分は通常はない。 (3) 1667 MHz 超微細構造が 1992 年 10 月にだけ現れた。 1665 MHz メーザーは FIR 光で励起されると考えられる。もし、新たなダスト が内側シェルで形成されれば、FIR 放射が増加するだろう。1992 極大時に 新しいダスト塊が現れたというダスト塊はこの描像に一致する。 モニタリング 1992 年事象のようなときには大量のダストが形成されると思われる。 そのような時のモニタリング観測でできる限りの情報を集めることが大事である。 このような極大は 3 - 4 サイクル毎に起きる。 |