| ミラ型星 AU Cygni (P=435 d) の IRAS LRS 各回スキャンから、その F12 と 10 μm 放射帯コントラストが可視変光曲線と共に変化することが判った。 | F12 はファクター 1.7 変化し、コントラストは 40 % 変わった。ダスト放射 の変化は Leung コンピュータコードでモデル化された。 |
|
観測時期 11か月の観測期間中に IRAS は AU Cyg に対し PSC フラックス測定と LRS スキャンを5回づつ実施した。うち三回は極大近く Φ = 0.18, 0.18, 0.20, 二回は七か月後の極小に近い Φ = 0.58, 0.58 であった。 それらのスキャンを図1に示す。 コントラストの定義 可視変光曲線の比較から、F12 は約 0.6 mag の振幅の変光を示すようで ある。コントラストは、極大付近で 1.12 から極小近くで 0.71 へと変わる。 |
コントラスト=(Fλ-FBB)/FBB
で定義され、ここに FBB は放射帯の左右でフィットするようにした。コントラスト =0 はゼロ放射帯に対応する。 (1992 年の定義では黒体を引いて いなかったんですけど。定義変更の挨拶くらいしろよ。) Leung コード モデル計算には Leung 輻射輸達コード CS-DUST3 を使用した。 中心星放射には黒体を仮定し、ダスト放射率には Draine (1985) の変更シリケイトダスト放射率を使用した。データフィットのため、 Ts = 星有効温度, Rs=星半径, Rin = シェル内縁半径、τ10 = シェルの 10 μm 光学的深さ, をパラメタ―として用いた。 |

|
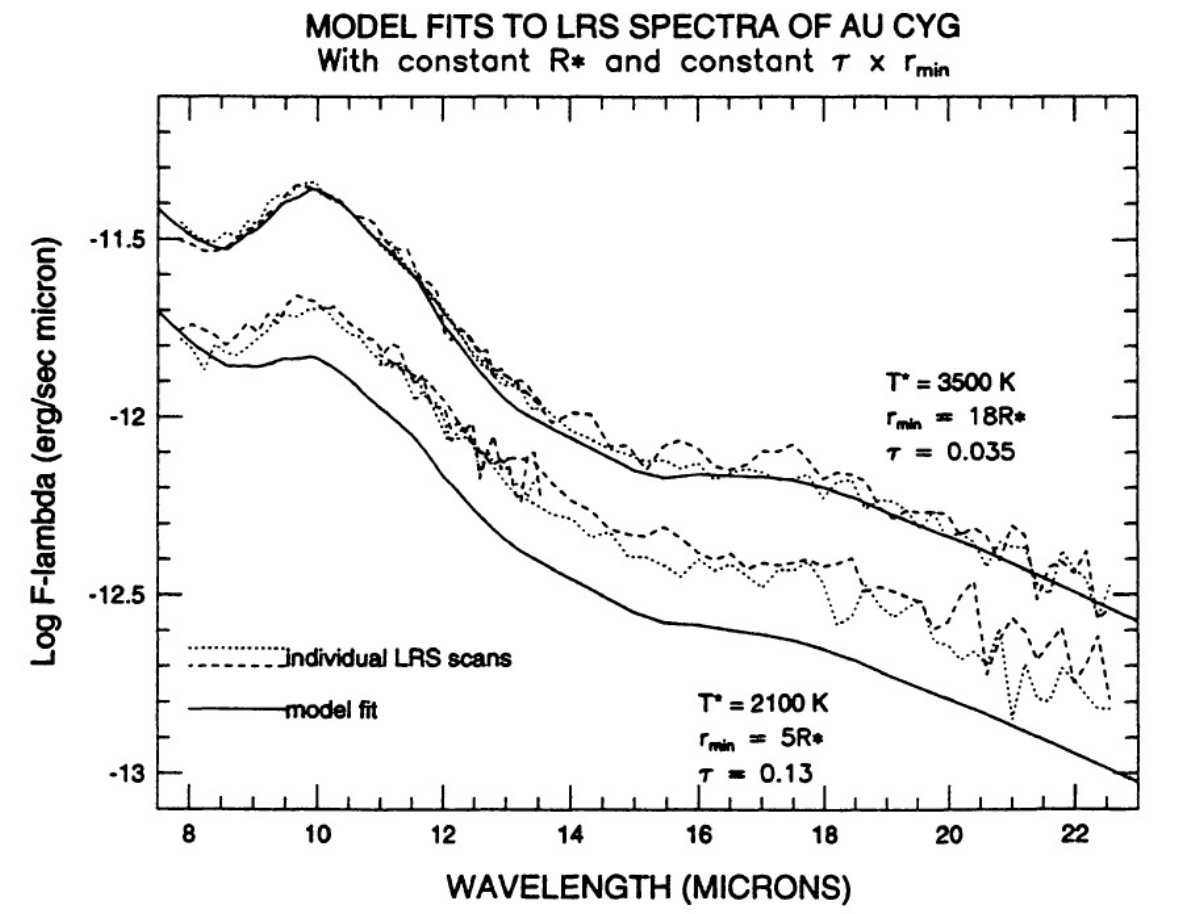
フィットパラメタ― 極大付近 (Φ=0.18) では、Ts = 3500 K, Rin = 18 Rs, τ10 = 0.035 である。Rin でのダスト温度は Tin = 680 K. 極小付近 (Φ=0.58) では、 Ts = 1800 K, Rin = 2 Rs, τ10 = 0.80 である。Rin でのダスト温度は Tin = 675 K. 極小モデルはフラックス変化 0.6 mag とコントラスト変化を再現するという 制約が与えられる。 フィットの結果 AU Cygni の 8 μm フラックスがファクター 1.9 変化するので、 Ts には大きな変化が要求される。我々がシリケイト放射帯の十分な コントラストを得るための最低星温度は Ts = 1800 K である。極大時温度 3500 K で、我々が得た恒星半径の変化は 7.5 % で、ミラでの変動の ファクター 2 (Hoffmeister 1985) に比べると著しく小さい。 (理解できない。 Rs も変動パラメタ― とは前に書いていなかった。) |
物理モデルになっていない? LRS データにはフィットしたが、それは物理モデルにはなっていない。もし 放射率 Q とマスロス率が変光サイクル間で一定、つまり密度が R-2 型、とすると、τ10Rin = 一定である。図1には、この制限で LRS へのフィットを示す。この制限下では極小時フィットは非常に悪い。 どうすべきか? 極小時 LRS を十分にフィットするためにはダスト密度を約 3 倍に上げる 必要がある。別の可能性としては極小時のダスト放射率 Q を、 Le Betre 1993 が示唆したように、上げることがある。 10 μm 放射はかなり薄い層から出ている。変光サイクルの間、グレイン マントルが部分的に蒸発して、異なる Q を持つダストコアが露出し、放射 特性が変化する可能性もある。また、 Day 1976 や Nuth, Hecht 1990 が 指摘した F(10)/F(18) が温度により変わる効果もまだ未研究である。 |