|
銀河系反中心方向の 21-cm 観測が Dwingeloo 25-m 望遠鏡で行われた。
目的は速度からこの領域の天体成分を分解することである。ラインをガウシャン
で分けて、(l, v) 図上で解析した（図６）。それらの成分の（ｂ、ｖ）上の性質
を表２にまとめた。 良く知られたペルセウス腕、オリオン腕、それに腕 F, 腕 I に加え、三つの細い 腕が銀河面とはずれて存在し、反中心方向でこちらに接近する速度を示す。 |
これ等の内、最も極端な成分は l = 180 で b = -9 まで下がり、視線速度 -29.5
km/s を示す。この腕はライデンマップ上で最も外側の腕の延長を成している。
銀緯方向に大きく広がった二つの成分もある。一つは異常なほど速度分散が小さい。 これは近傍の年齢 70 Myr の膨張リングではないか。もう一つは微かで、速度分散は 19 km/s と大きい。これは腕間ガスかも知れないが、その性質は不明である。 |
|
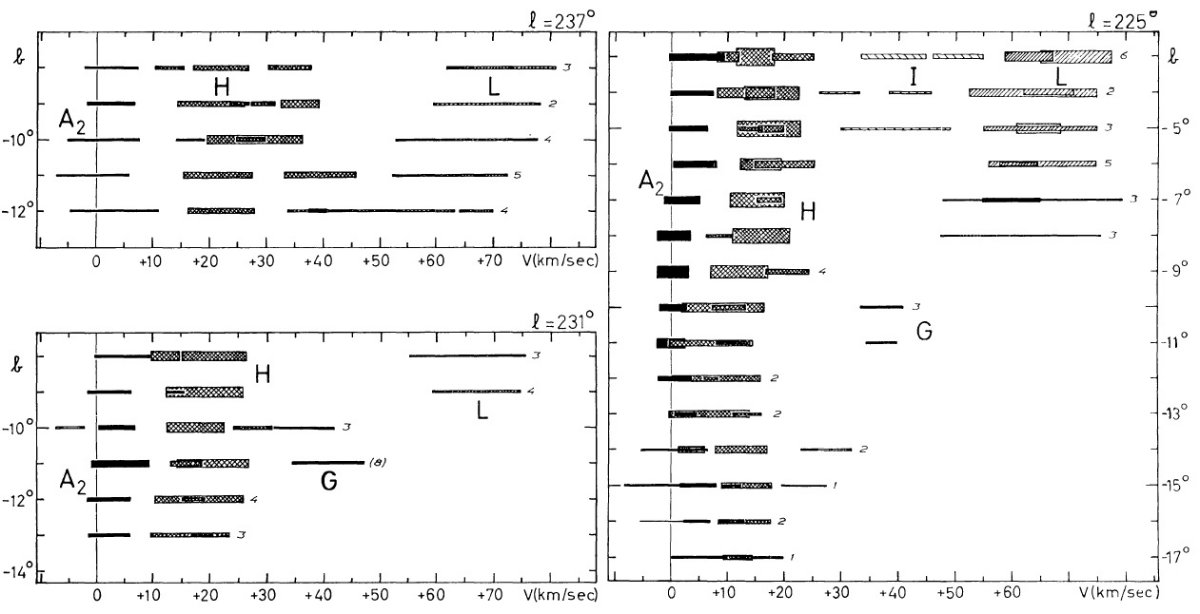
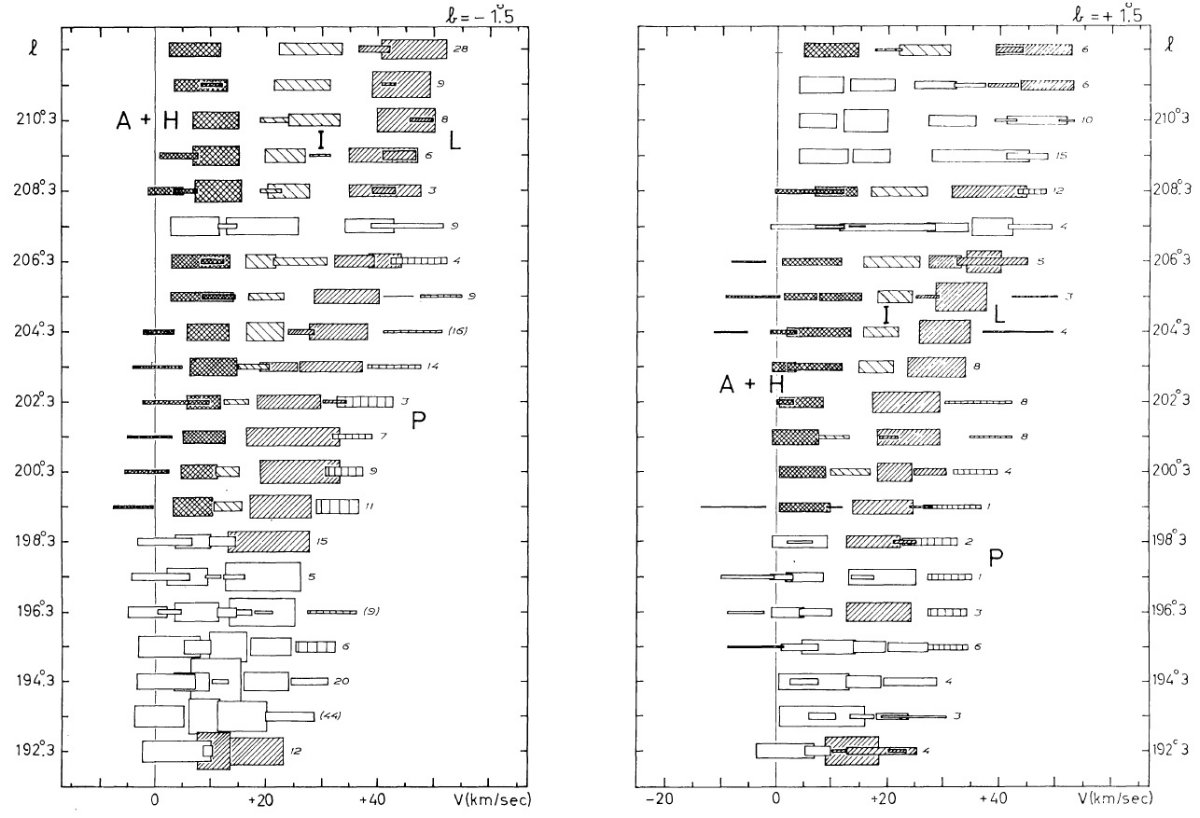
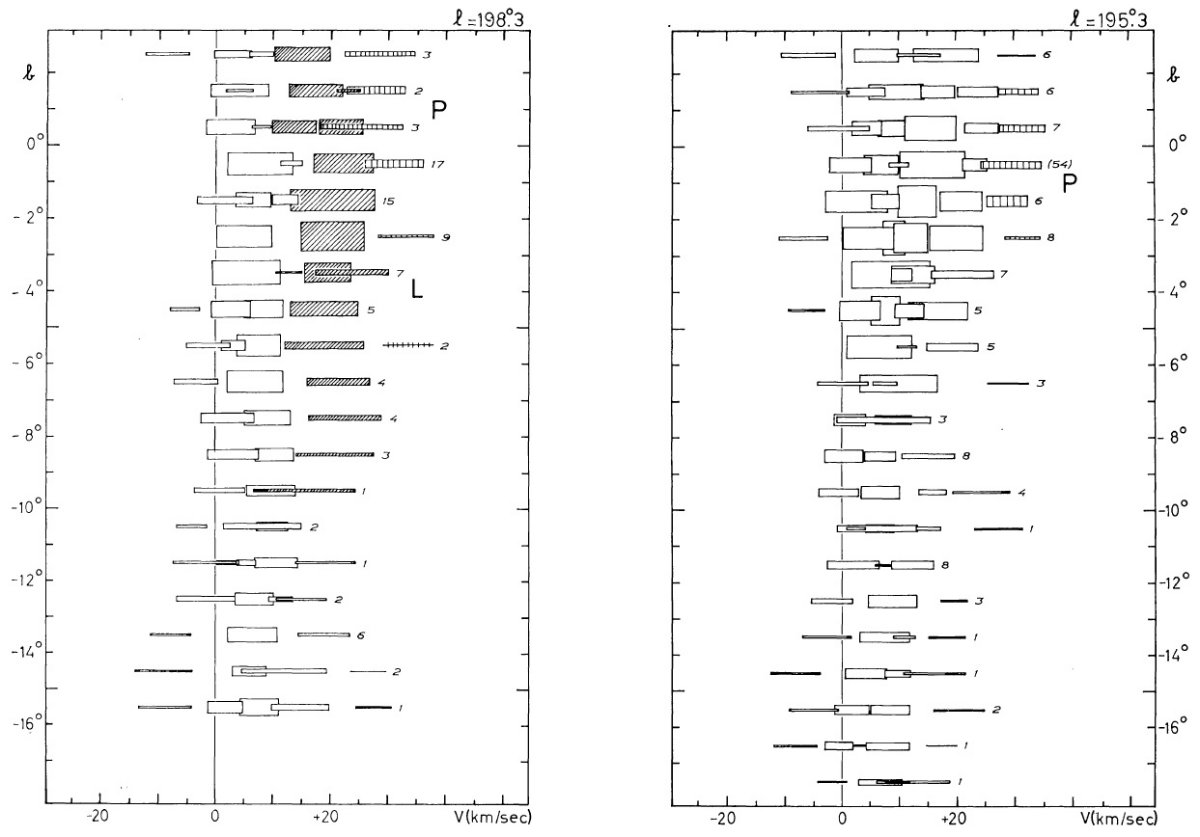
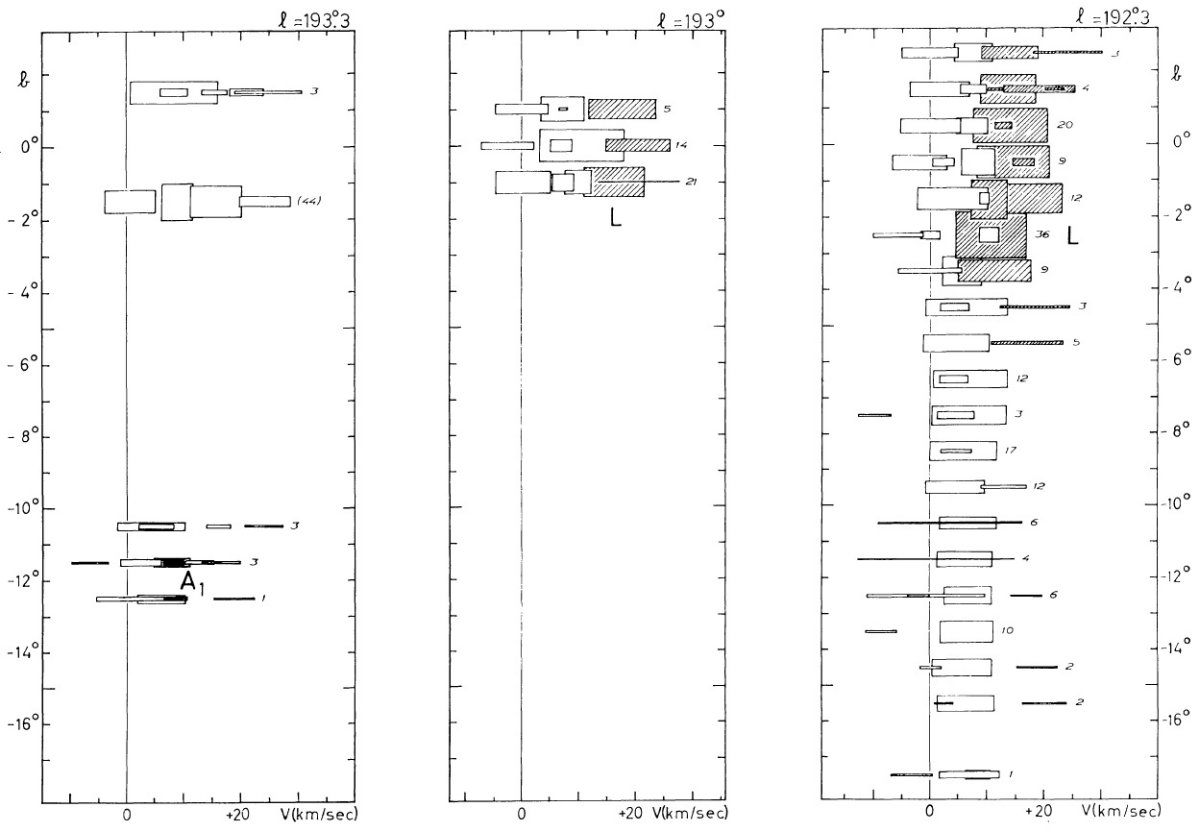
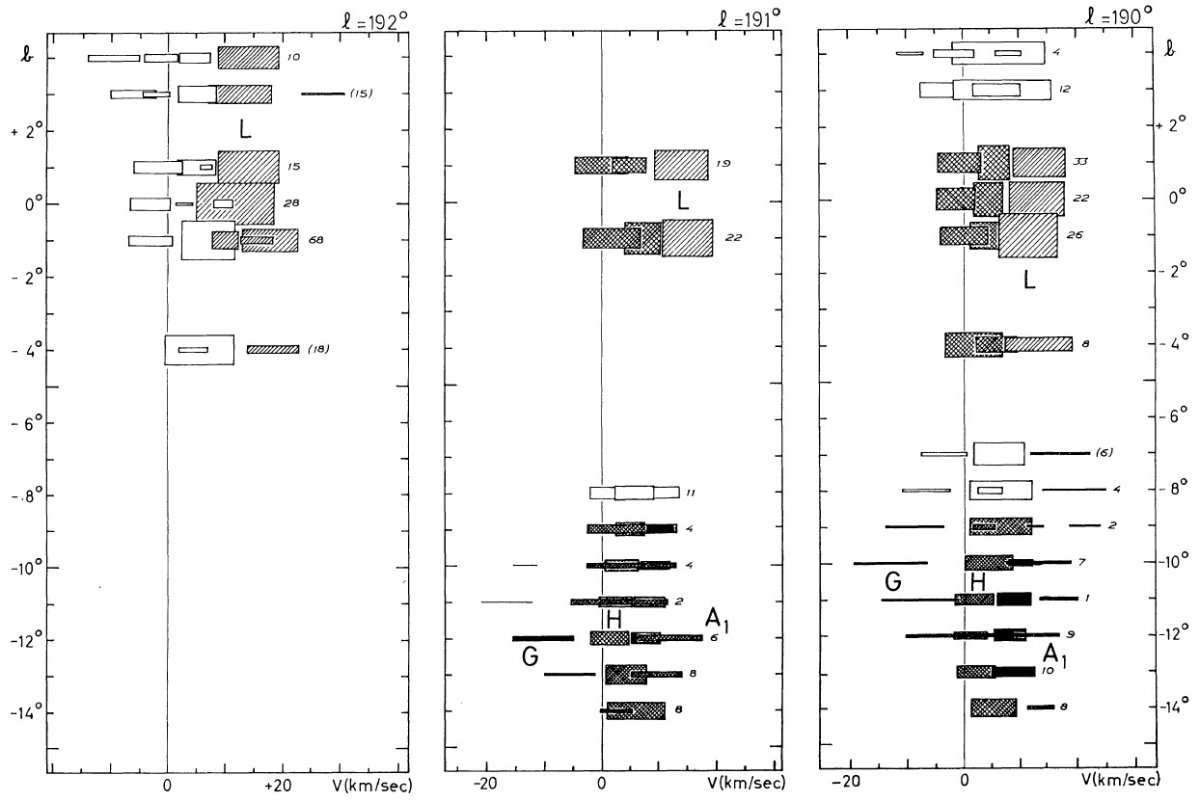
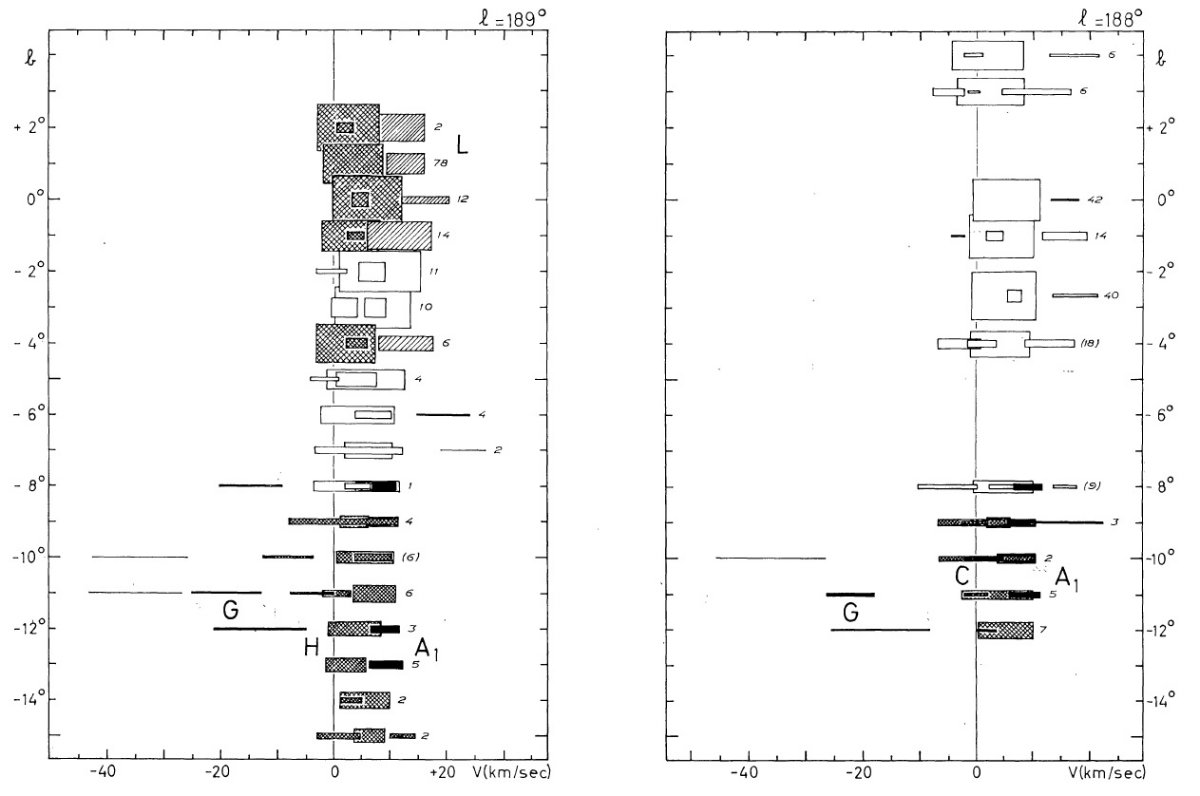
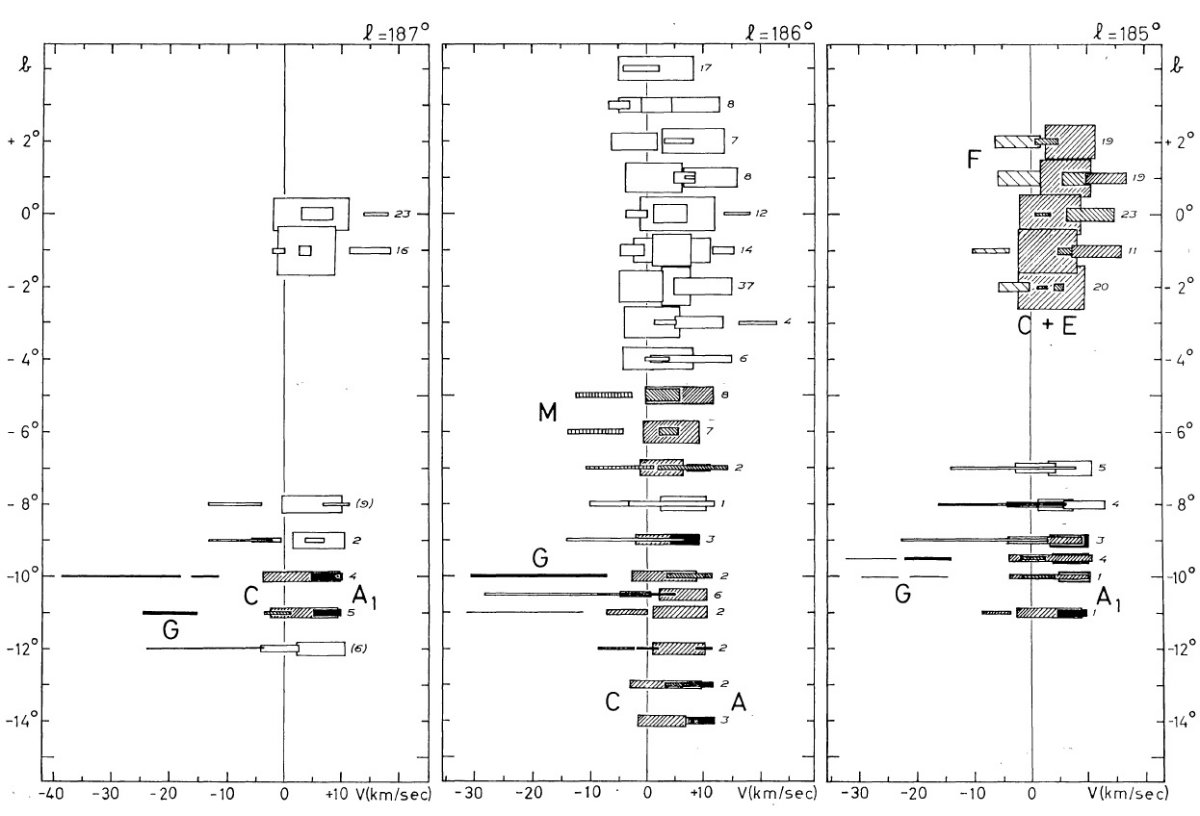
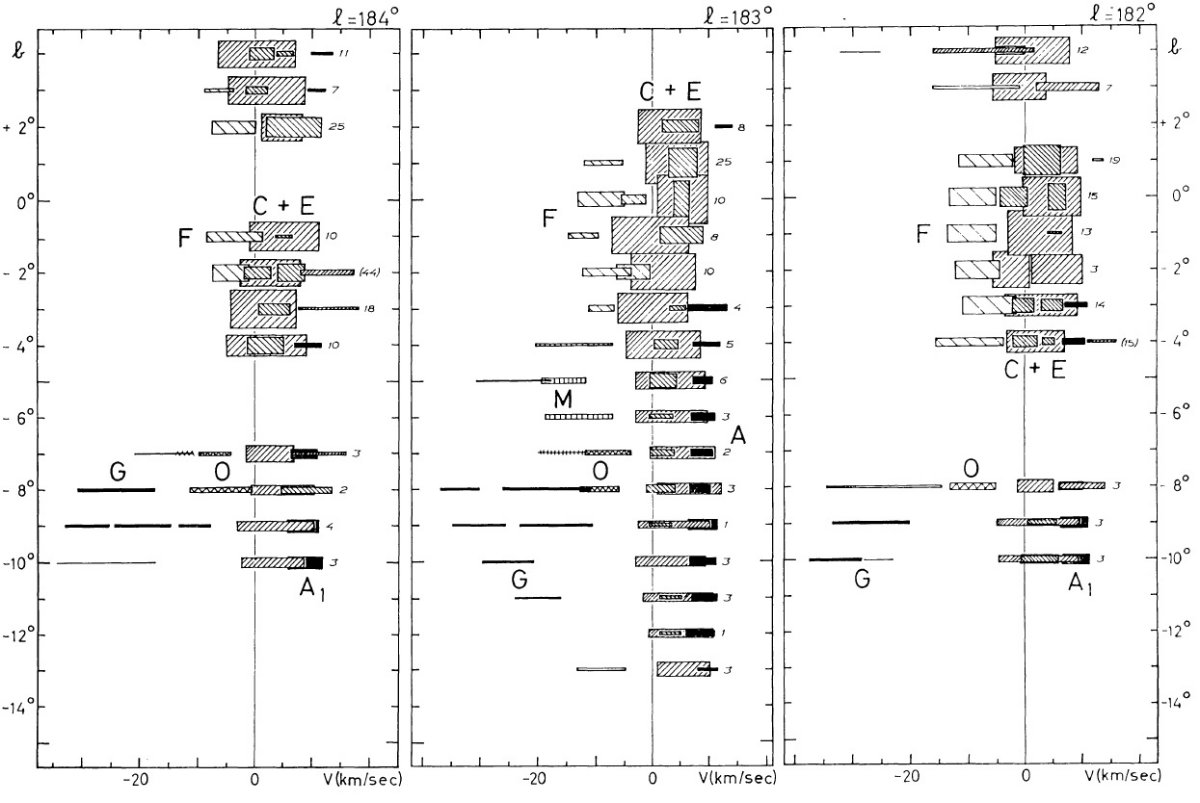
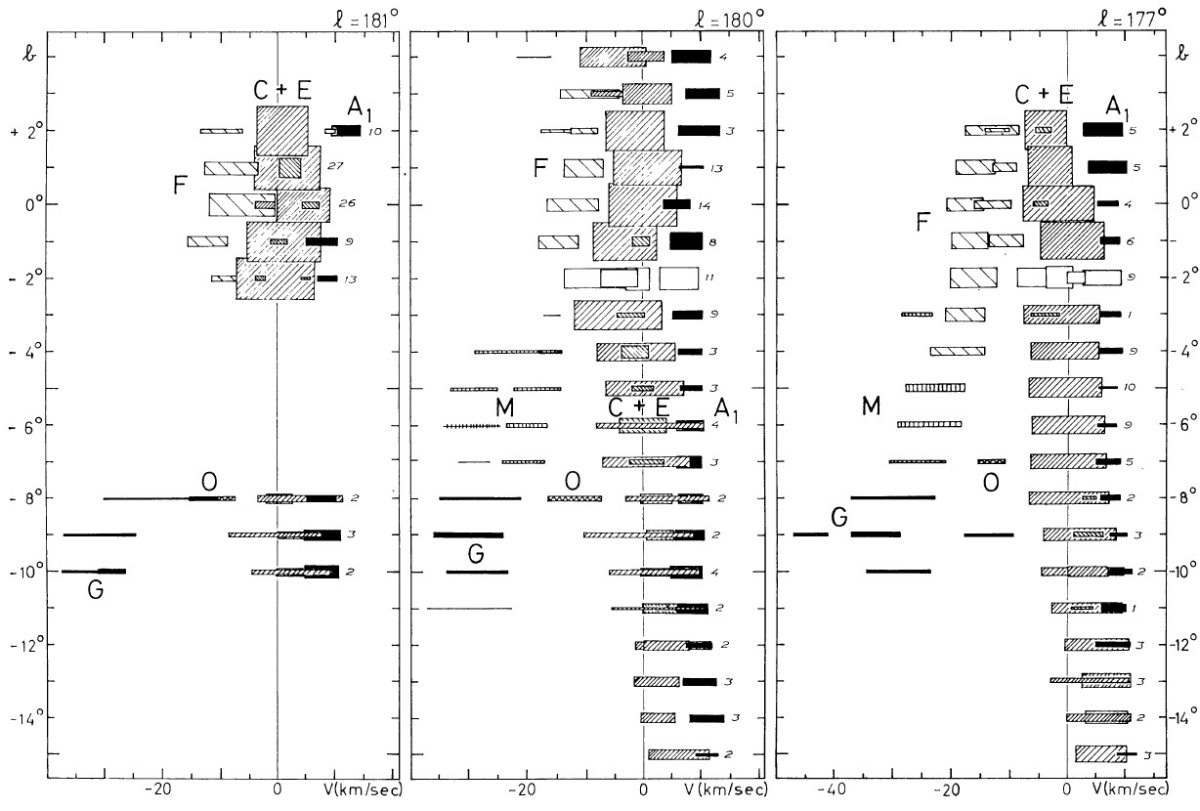
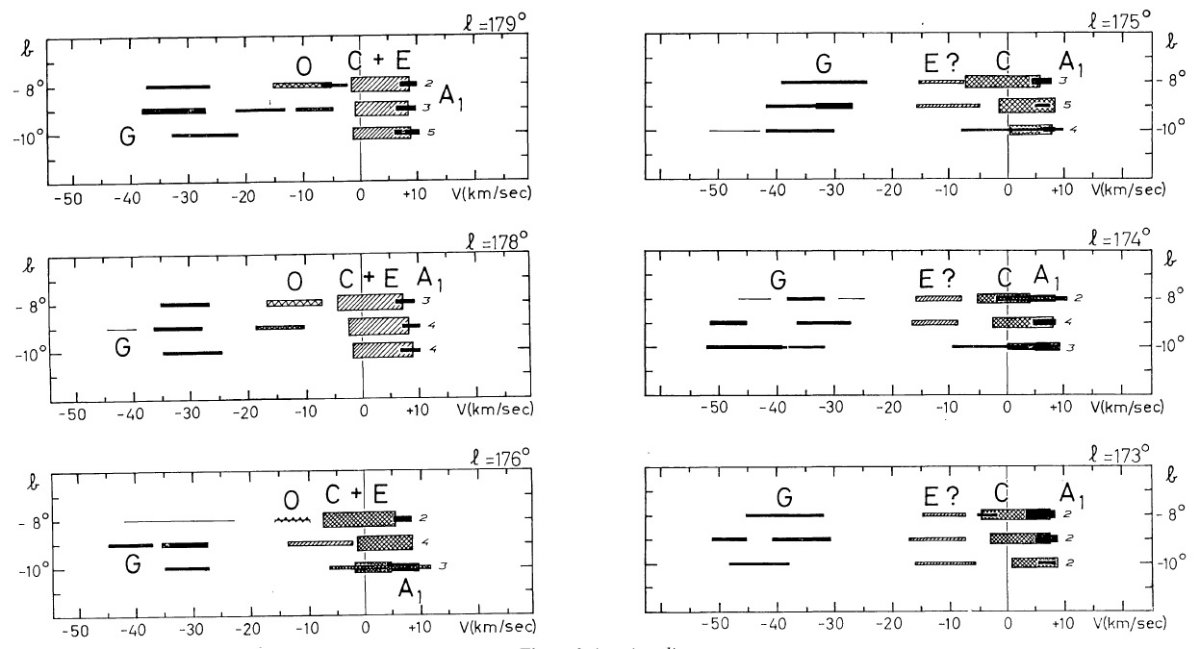
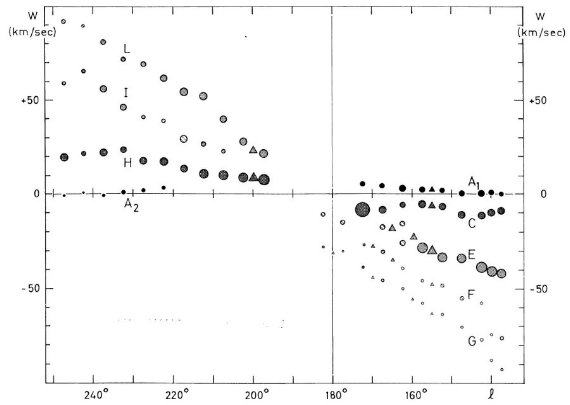
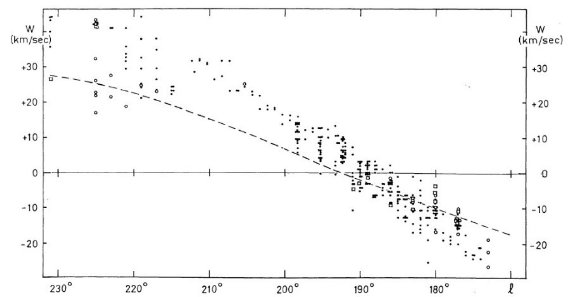
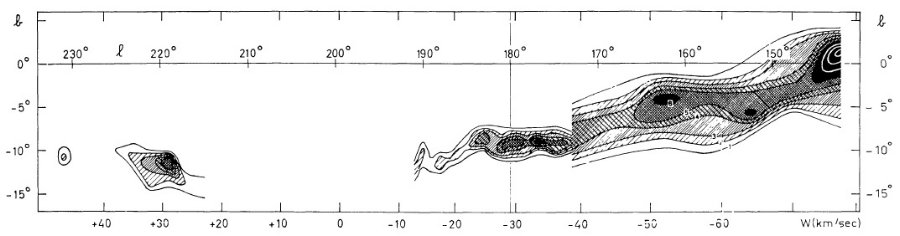
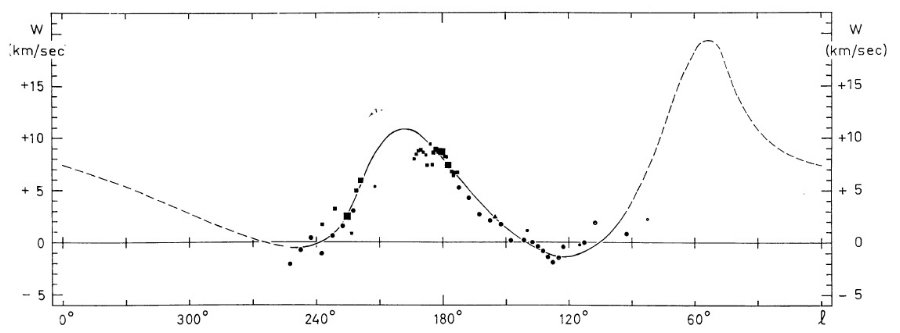
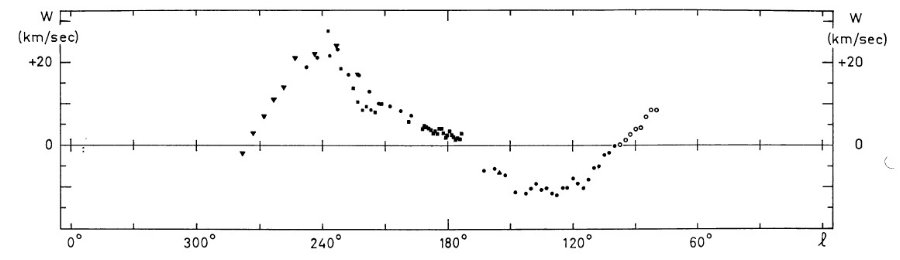
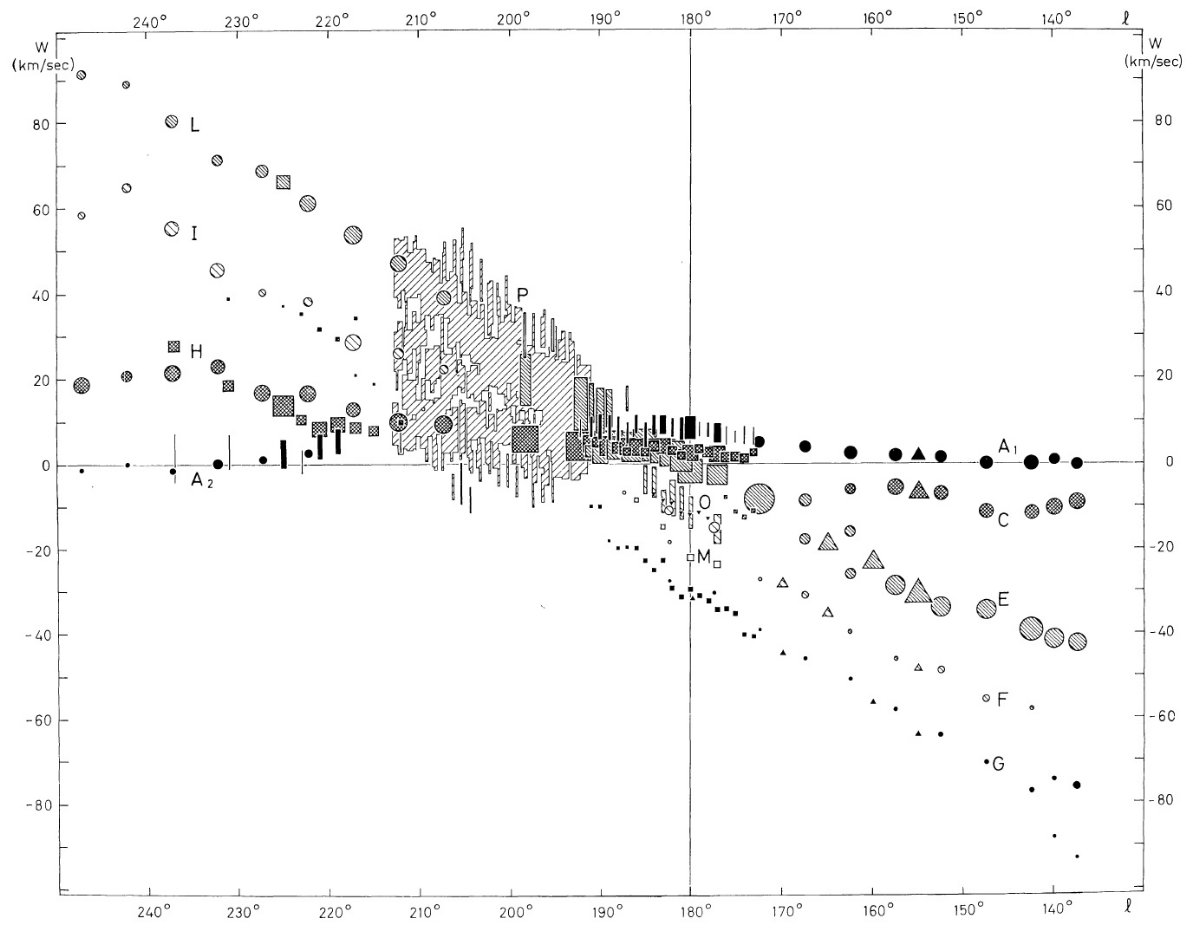
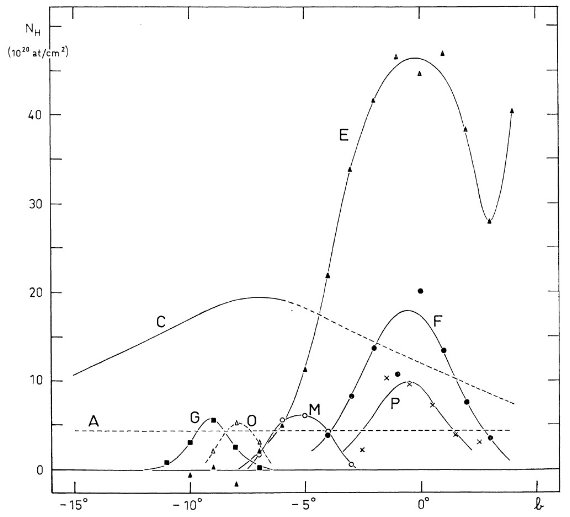
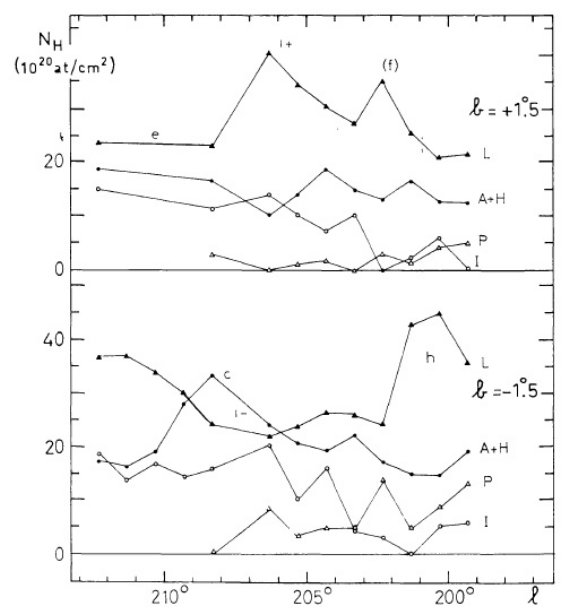
HI 空白部 HI 観測から銀河構造を導く際に問題になるのは、銀河中心方向と、反中心 方向である。そこでは、円運動からの小さなずれが距離決定に大きな影響を 与えるからである。そのため、両領域は空白にされるのが通例である。 円運動からのずれの直接観察 この方向が興味あるのは、円運動からのずれが直接観察できるからでもある。 特に反中心方向は負視線速度のずれが最大であるという興味深い現象が見られる。 最外側腕を追跡 観測の第１目標は、ライデンマップの最外側腕を追跡することである。反 中心方向ではこの腕は 30 km/s の接近を示し、かつ銀緯 -9° まで下がる。 これは Westerhout 1957 pp221 に明らかであるが、ここではより高分解能の 速度観測を行う。 速度分解能を上げる 第２目標は (l, v) 図の分解能を上げることである。このためガウシャン分解を 観測各点で試みた。それら観測点を下に示す。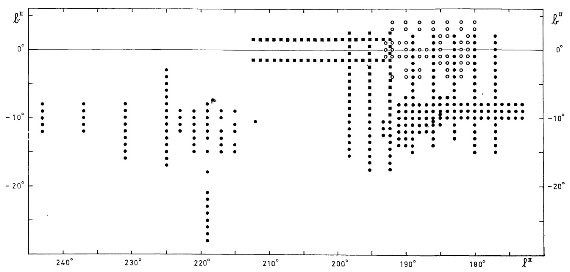  図１．ガウシャンフィットで速度分解を行った観測点の位置。 |
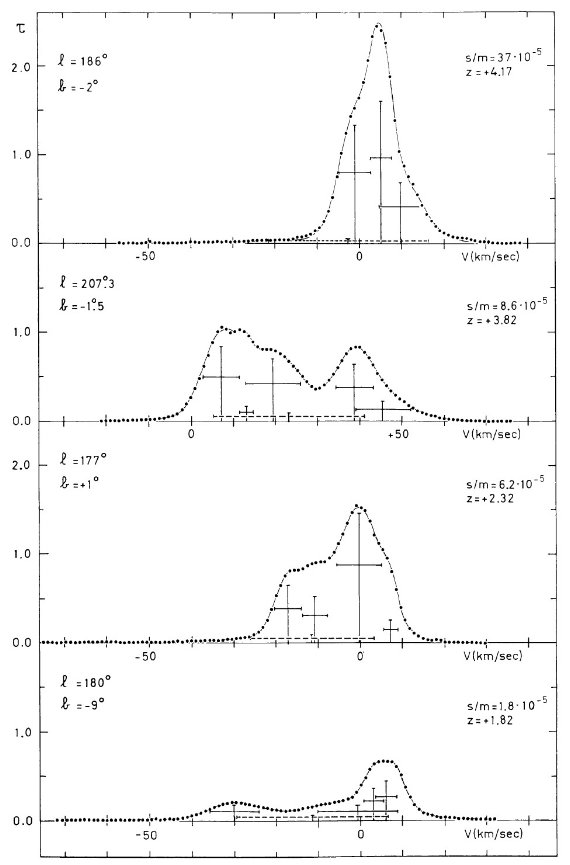
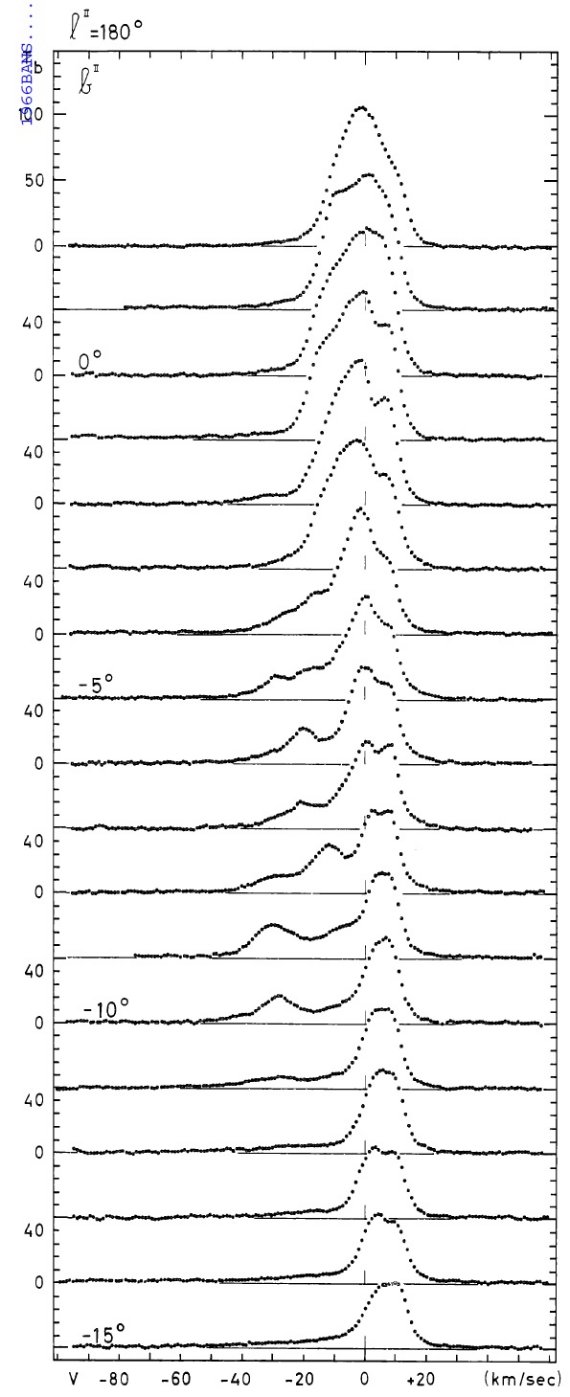
 図２．ガウシャンフィットの例。点線＝観測プロファイル。十字の縦棒＝ 定数項。横棒＝2 × σ |
|
名前の付け方 今回の研究では先入観を排除するため、わざと電波特徴には Hoglund 1963 のアルファベット名を採用した。図４には、丸＝Kootwijk サーベイによる、 三角＝Hoglund サーベイによる各成分の速度を示した。 A1 と A2 l < 160° と l > 220° では図中で異なる名前の特徴は互いに 離れていく。A1 と A2 は速度分散が狭く、銀緯方向の広がりが大きいのが 特徴である。その強度は b = [-10, +10] でほぼ一定である。これら二つはおそらく 同一の局所天体であろう。その空間分布を円運動の仮定から導くことはできない。 このため、Westerhout 1957 はこの特徴を彼の議論から省いた。 C と H C と H はより大きな速度分散と b の HPW = 10° という大きさを示す。 これらは一緒になって所謂オリオン腕＝局所腕を作っている。 E, F, I, L E, F, I, L の b 方向 HPW = 5° - 7° である。 E は非常に強い。 一方 F は非常に弱く、 l = 142° の先には追えない。E はペルセウス腕を 作る。Westerhout は L をその反中心の反対方向への連続と考えた。一方、I は 中間腕（intermediate arm）と呼ばれる。Hoglund は E の連続は L ではなく、 Ｉ であると考えた。 Ｇ Ｇは銀緯巾はやや狭い。これは外側腕＝ outer arm の継続を作っている。 これには二つの異常がある。 （１）反中心でかなり大きい v = -30 km/s を示す。 （２）l = [140, 180] の間に平均銀緯が b = 0° から -9°に落ちた。 |
 図４．反中心近くの (l, v) 図。丸＝Kootwijk サーベイによる。三角＝ Hoglund サーベイによる。濃い斜線＝銀緯(b)角が大。マークの面積は 夫々の特徴の表面密度を表す。影が濃いほど銀緯見込み角が大きい。 |
|
ウィング Lindblad 1966 の l = [177, 191], b = [-15, -13] のラインプロファイル を見ると、低輝度だが広いウィングがマイナス速度の方に伸びているのが見える。 銀河面に近づくと、この広いウィングは銀河面の下に現れる分子雲の強い光に 消される。Lindblad 1964 はこれを銀河面を覆う希薄な円盤からの放射と考えた。  図５．構造 B の (l, v) 図。四角＝信頼できるデータ。丸＝やや怪しい。 点＝大いに怪しい。 |
 Lindblad 1966 の図2．Dwingloo 観測アトラスの一部。 b = [-15, -13] のマイナス速度に広い ウィングが見える。これが構造 B である。 |
図３で濃い四角が構造Ａである。そのガウシャンフィットパラメタ―を図６
では (l, v) 図上にプロットした。図７には成分の平均密度をプロットした。
 図７．構造Ａの表面密度の銀経による変化。丸の大きさは寄与したラインプロ ファイルの数を表す。 |
図７，８を見て、著しい逸脱箇所は見られない。構造Ａ１とＡ２とは
同一の天体が銀経で分かれて見えるだけと考えてよい。
 図８．構造Ａ表面密度の平均値からのずれ。 |
|
図中の構造Ｇ 構造Ｇは最もよく分解された構造である。それは、l = [173, 188], b = [-11, -9] で強い極大を示す。速度は v = [-40, -20] である。 ( 図９では、 l = 150 付近にずっと強い 山があるが？) 本研究の目的の一つはこの腕の研究である。図３でこの腕は黒三角で表されている。 ラインプロファイルを調べると、この構造は２または３の成分から成る。図６では その重み平均を黒四角で示した。 構造Ｇの表面密度 図９には構造Ｇの表面密度分布を示す。平均視線速度も示した。 l = 140 ではこの腕は銀河面上にあり、ｖ = -80 km/s である。そこから腕は銀河面の下 に潜り始め、反中心方向で b = -9, v = -30 km/s に達する。その先も l = -192 まで辿れるが、強度は弱い。図９左、Dwingloo 観測は分解能が高く、この腕が 細いことを示す。 平均表面密度の緯度変化 図１０では、l = 173 - 180 方向での各構造の平均表面密度の緯度変化を示す。 構造Ｇ の極大は b = -9,1, 値は 5.7 × 1020 cm-2 であった。腕の巾は HPW = 2°.0 である。速度分散は 5.7±0.2 km/s. 延長？ こうなると、さらに銀経が大きいところで、この腕が正速度側に再び現れるか が気になる。実際、l ≥ 215 で b = [-20, -10] に銀河面近くのガスとは分離 して、強度極大の連なりが見える。図３にはこの成分を黒三角で印した。図６と 図９ではこれが構造Ｇのちょん切れた繋がりではないかと述べてある。l = [219, 225] では速度は構造Ｇの延長上にきれいに載ることが図６に示される。しかし、この 速度は構造 I と一致し、これは構造 G の低銀緯部に過ぎないかも知れない。 |
 図１０．反中心方向での各構造の平均表面密度。 |
４．５．構造Ｆ構造Ｆは l = 177 で強い独立した極大として、主極大の低速度側に現れる。 銀緯は b = [-3, +2] で l = [177, 183] で見られる。l = 177 と 183 では ２成分が認められるがどちらも構造 F とした。 ４．６．構造Ｍl = 177, 180, 183, 186 では、構造ＦとＧの間に、強度極大を b = -5 付近 に持ち、v = [-24, -8] の成分がある。これは構造ＦかＧと関連する可能性も あるが、未確認の内は一応別個の構造として扱う。４．７．構造Ｏl = [177, 184]、b =[-8, -7] , v = [-14, -6] km/s にかなり孤立した 極大が見える。多くの場合、極大は b = -9 に現れる。４．７．構造ＨＨ の要素l ≥ 219 では、これは A2 と分離して見える。l = [199, 217] では Ａ２ とは混ざってしまうが、I, L とは分かれて見える。 l ≥ 212 では 観測が銀河面下では限定された距離内である。l ≥ 225 ではラインプロ ファイルがいくつかに分裂してしまう。 図１１ 図１１には b = 1.5 と -1.5 でのいくつかの構造の表面密度の変化を l = [199.3, 212.3] で示した。 |
 図１１．一角獣座における幾つかの構造の b = [-1.5, 1.5] 平均表面密度の変化。 |
４．９．構造ＣとＥl = [177, 185] に構造ＣとＥがある。４．１０．構造Ｌ |
 図１２． |
５．３．構造Ａの解釈局所性の単一雲図１６には構造Ａの (l, v) 図を示す。 l < 77 では観測がそこまで広く なかったために構造Ａは欠けている。ある個所では構造 C/H と分離が困難である。 観測から得た速度曲線は非対称に見えるが、大体はプラス速度側にずれた 2・l の調和関数で近似できる。たった 2.5 km/s という小さな速度分散はこの 構造が一つの雲から成るという印象を与える。速度の 2l 依存性と大きな 銀緯範囲は構造が局所性であることを物語る。これらの特徴を単純なモデルで 説明するには膨張シェルがよいだろう。 モデル Blaauw 1946, 1952 はアソシエイションのモデルとして、一点から等方的に 飛び出す星の運動を銀河円盤内で調べた。その結果をここで用いる。 座標系(ξ, η) を太陽を中心に銀河回転に乗って回転する座標系とする。 ξ = 銀河中心と太陽を結び、外向きの軸。η = 銀河回転方向の軸。 t = 0 で星が等方的に速度 so で飛び出すと考える。 |
η 軸から ξ 方向に測った方位角 φ 方向に飛び出た星の初速度成分を
α=sosinφ, &beta:=socosφ とすると、星の
の運動は次の式で与えられる。
図１７はその解の数例である。t = 65 Myr のグラフは構造Ａを最もよく表現している。 図１６にはこのベスト解を拡大して示した。この解のパラメタ―は、 t = 65 Myr so = 6.2 km/s ξ1= -47 pc η1= -264 pc である。リングの長半径 = 650 pc, 短半径 = 280 pc, 反中心方向構造までの 距離は 530 pc である。 |
|
概要 腕１８は構造 C/H の (l, v) 図である。図の空白部では腕を追跡することは 非常に困難である。l < 90 では構造 C/H は構造 A と深く混ざり合ってしまう。 l < 75 では観測範囲が b = 5 以下と狭まるので、分離がさらに困難となる。 腕の逆端では視線速度が l = 270 でゼロになるのが明らかになる。 l = 280 付近で視線方向は腕の接線方向となり、そこでの速度構造は非常に複雑となる。 構造 C/H は腕なのか？ 図１８にはオリオン腕の太陽近傍付近の様子が示されている。この近傍性は l > 240 で視線速度の低下として強く表現されている。この構造が銀河腕の 一部であるという考えは、Westerhout 1957 が行った、 l = [73, 90] の混雑した 領域における、光学的深さの速度と銀緯依存性の研究に発している。そこでは 太陽からの距離の見積もりは円運動からの小さなズレに大きく影響される。 この研究では、構造 A と C、それにより狭い銀緯分布を伴う構造は全て、オリオン 腕に属すると考えていた。ライデンマップに描かれていたようなオリオン腕 はまだ完全に確実ではない。 |
オリオン腕の位置 図１８の l = [90, 270] カーブと合うオリオン腕の形は、半円を l = 240 方向に引き伸ばしたようなものである。l = 180 における (l, v) の勾配は、 反中心方向では観測が系統誤差の影響を強く受けるので、非常に決めにくい。 表２では +0.29 km/s が示唆されている。これは式 (10) 右辺の第１項だけ 生かすと、構造までの反中心方向距離 560 pc を与える。この値は前に述べた 構造 A までの反中心方向距離 530 pc と非常に近い。従って、構造 A と構造 C/H のガスは独立に扱う訳にはいかない。 |
|
円運動からの目立った逸脱はない E/L 腕の速度曲線は図６にある。 l < 130 では腕の視線速度は分裂する。 観測点を結ぶ滑らかな曲線を描き、反中心方向では構造 C の影響で少しプラス 側に速度がずれることを考慮すると、 l = 180 での構造 E/L 速度として、 -2 km/s を得る。つまり、 E/L 腕には円運動からの目立った逸脱はない。 |
距離 腕までの距離を円運動の仮定で求める。回転曲線の l = 180 での勾配は、 +1.22 km/s/deg である。 v = vo = 0, du/dθ = 0 の仮定 で、式１０から Ro(ω-ωo) = -70.1 km/s を得る。 これは腕の銀河中心距離 12.9 kpc を与える。 |
| これ等の構造を光学同定することは最も重要である。 |