
| 1982 - 1987 年の間に取得した炭素星ミラ R For の可視・赤外測光データを 示す。異なる変光位相での SED を輻射モデルを用いて解釈した。極小付近に おいて、中心星が隠される現象は星周シェル内側部でのダスト凝結で説明され る。この凝結は単に光度低下に伴う温度降下の帰結であろう。 |
極大と極小間で総光度は 2.3 倍変化する。1 μm 光学的深さは極小期に
1.0 極大期に 0.7 である。赤外カラーの変化は質量流出が一様と云う仮定と
合う。 Feast et al 1984 が報告した 1983 年極小の異常な暗さが再確認
された。これは提出したモデル内で説明可能であり、余分の独立シェル放出
や、ダスト雲による食を考えなくてよい。
(
光度低下の実証がポイントになる?mbol 変光曲線がこれで描けないか?
) |
|
R For = IRC-30021 = GL 337 = IRAS02270-2619 は、
(RA, Dec)1950 = (02h27m01.31s, -26°19'14".8), P = 388 d, で
ある。 Feast et al. (1984) は R For のモニタリング観測から 1983 年末の特に深い極小を 星周シェルの遮光が変化したためと考えた。 | その原因として、(i) 新しいシェルの放出, (ii) 既存シェル内でのダスト 形成, (iii) ダスト雲の通過, (iv) あちこちに放出されるダスト雲塊が こっちに向かった。この論文は第2の可能性が最も論理的でかつ観測と 合うことを示す。 |

|
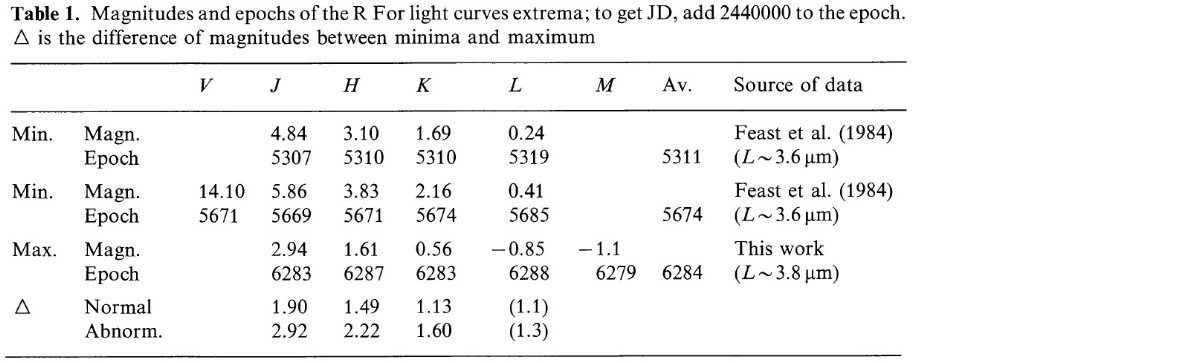
測光 観測は ESO 1 m 望遠鏡の標準測光器で行われた。U,B,V,R,I 測光は3回、 J,H,K,L,M は 18 回、N, N1, N2, N3, Q0 測光は 7 回行われた。 図1=測光結果 測光結果を図1に示す。回数は少ないが、周期性は明らかである。 Feast et al. (1984) の 1982-1983 データも図1に示す。彼らの J,H,K 測光と我々の 結果の一致は良い。明らかに 1983 極小は通常より暗い。この減少は 短波長ほど大きい。 |
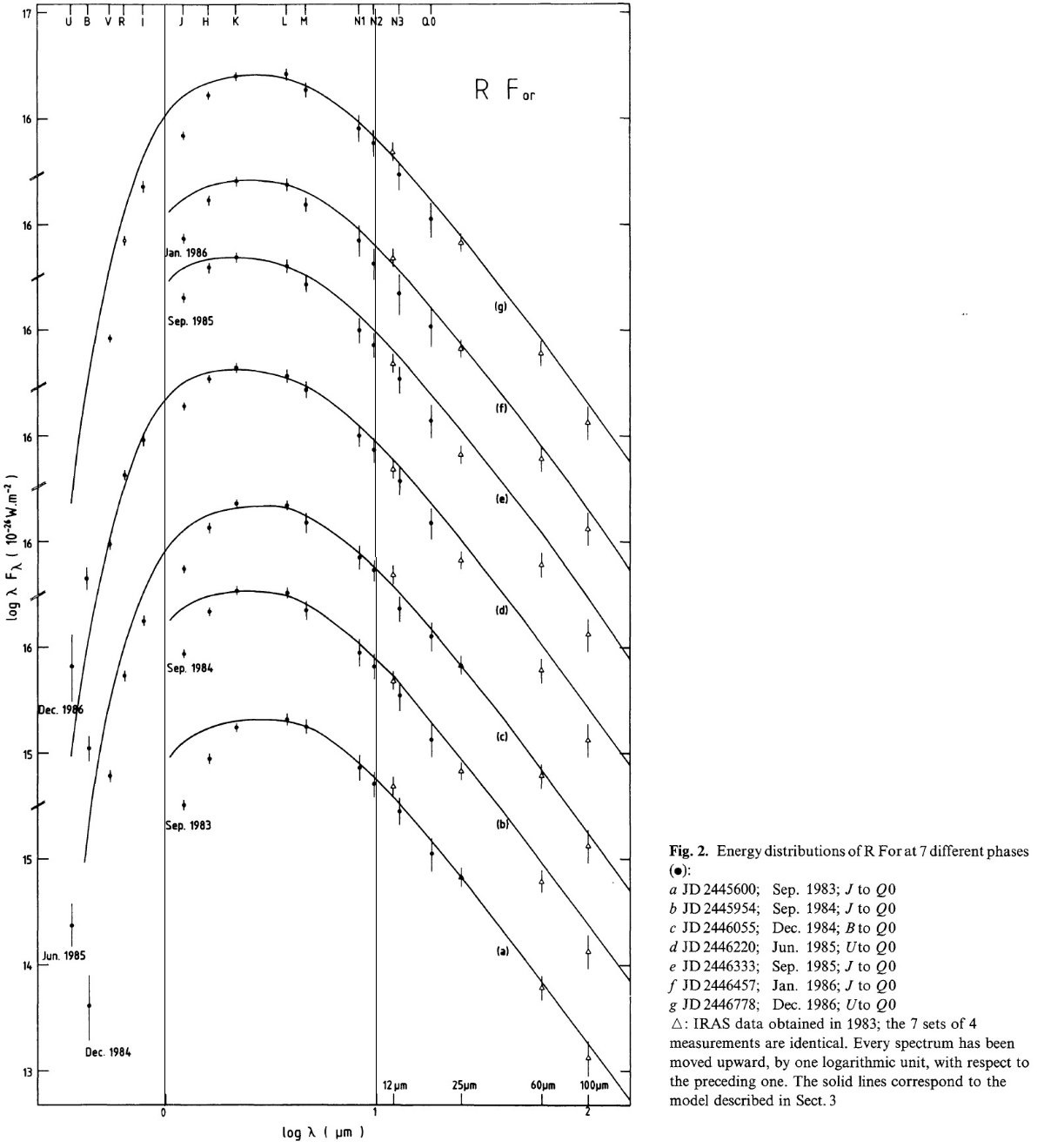
観測位相 図2には 7 時期の 1 - 20 μm SED を示す。全体は 1200 - 1400 K BB で近似できる。1985 年極大スペクトルはピーク 2.5 μm, 1984 年極小スペクトルはピーク 2. μm, 1983 年の異常期極小スペクトルはピーク λ > 3.2 μm, である。 1984 年 12 月、1985 年 6 月、1986 年 12 月 に、 1 - 20 μm とほぼ同時期に可視測光が行われた。IRAS は 1983 年である。 図1を見ると、これらの観測は下降期の中頃に撮られた。しかし 変光振幅は波長と共に小さくなるので、遠赤外での変光は第1近似では無視す る。こうして、7 スペクトルの FIR 域は全て IRAS データで補完されること となった。 |
|
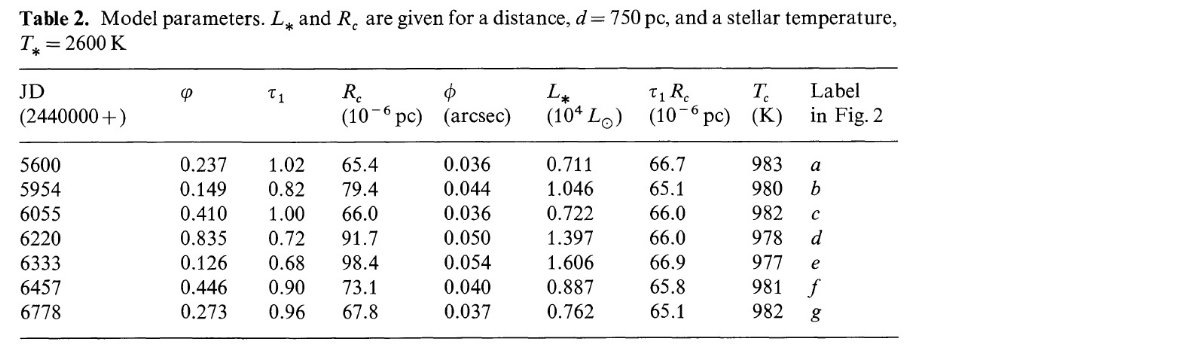
モデルの仮定 Le Bertre 1984 は Leung 1975 の方法を用いてダストシェルモデルの計算 プログラムを開発した。このモデルは、 (i) 星は Ts の黒体。 (ii) グレインが凝結温度 Tc 以下となる Rc とで存在する。 外側半径は SED に効かないので Ro = 10000 Rc に取り敢えず。 (この Ro が小さいというのが 最近の問題。 ) (iii) 密度分布は逆二乗則=一定速度 Ve の膨張。 ダストは形成後数 Rs で Ve に達する。 (ダスト形成域と加速域の密度分布 は要検討? ) (iv) 時間変化 マスロス率は周期 P のタイムスケールと永年変化 T (>P) のタイムスケール で変わる。この事実を念頭に (iii) は、変光周期は十分短いので VeP < Rc, かつ永年変化は十分遅いので Rc < VeT なために、 全体的な逆二乗則がダスト輻射領域で成立すると理解する。 天体の物理量 各数値計算のパラメタ―は、 Ts, Ls,τ1=τ(1μm), Rc(Tc と同意義) である。Cohen 1979 は晩期型炭素星の平均有効温度 Ts = 2600 Lo, Ls = 104 Lo とした。この計算でも平均値としてこの値を使う。 それから導かれる R For の距離(b=-68.2°)= 750 pc である。 |
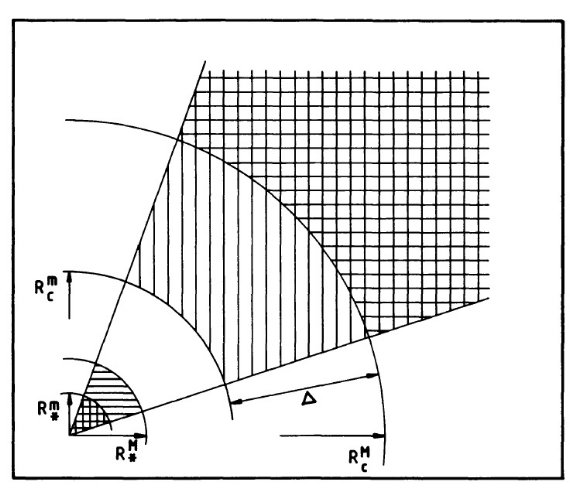 図3.変光極小から極大に移る時、 星半径は RsmからRsMへ、 シェル内側半径は RcmからRcM へと変わる。厚み Δ の層でダストは消えたり出来たりする。 縦縞=極小、横縞=極大。 |
|
ダストパラメタ― ダストのオパシティは Jura 1984 を採用し、 Q&lambda ∝ λ-1.3 とする。ダスト凝結温度は IRC+10216 の Le Bertre (1987) モデルから Tc = 900 - 1000 K とする。 |
変光の効果 Lsーー>Rcーー>τ1 なので、Ls の変化がモデルの 変化を生み出す。表2に我々が提案するモデルを示す。 図2にはその結果のモデルスペクトルを実線で示す。Tc = 980 K, τ1Rc ∼ 66 10-6 pc である。 変光位相 ψ は P = 388 d を仮定し、表1にある 1985 年の極大(ψ=0) から決めた。この表式では φ = 0.45 が極小となる。 (Ls は φ から決めたのか、それとも直接積分? ) ψ = 2 Tc/d = 内側空孔の視直径である。 |
|
(
ΔR = RcM-Rcm
と VeP の大きさの比較はどうなのか?この大小関係は大事そう。
) 赤外フィット モデルは全体として満足できる。赤外では J と H が暗いが、これは分子バンドの ためと解釈できる。 Feast et al. (1984) は 1.2 - 4.1 μm CVF スペクトルを取得した。それらは 1 - 2 μm 帯 に CN, C2, CO のバンドを示し、J, H 等級に影響するに違いない。 CN, CO は 2 - 4 μm 帯にも現れるが弱い。3.1 μm の深い C2H2, HCN バンドは L フィルターには重ならない。 10 - 20 μm 帯では調整は観測フラックスに関して少し超過である。これ は 0 等星のフラックスを少し低めに見積もったためかも知れない。 1983 年 9 月に対するモデル (a) は IRAS フラックスと合う。他のケース で合わないのがあるが、変光の効果だろう。 可視フィット 可視域の SED は星光球からの寄与が支配的である。炭素星の可視域は CN と C2 吸収を示す。λ 0.5 μm では C2 吸収 が非常に強い。モデルは BB を仮定しているので、U, B では観測に比べモデル は強い。 V, R, I バンドは相対的に分子吸収の効果は弱い。 内側半径の変化 R For に関して内側半径の変化を見積もると、極小から極大に掛けて Rc は 30 10-6 pc 動く。一方その間にマスロス流の動きは Ve P/2 = 8 10-6 pc である。従って、極小から極大の間に ダストの蒸発が起こる。 この研究でフィットしたモデルは 1983 年の 「異常」極小と同時期 またはその後での観測に対するものである。そのモデルが定常流の 1/r2 密度分布でフィットできたことから、 Feast et al. (1984) の説明 (1) = 新しい孤立シェルの放出はありそうにない。 また、低光度極小の時期と以前に放出されたシェルが Tc 位置に到達する時期 が一致するという偶然も首を傾けさせる。 ダスト雲による遮光という説明 (3), (4) は可能性としては残るが、不必要 に思える。また、遮光が低光度期と一致するという偶然は都合がよすぎる。 1983 年極小期の異常な暗さは中心星光度が通常の極小より低かったことの 結果として理解される。この低光度は Rc を縮小させ、光学的深さを 増大させる。第3章のモデルと表1の近赤外値を使うと、「異常極小」時には L = 5000 Lo, τ1 = 1.2 と予想される。 |
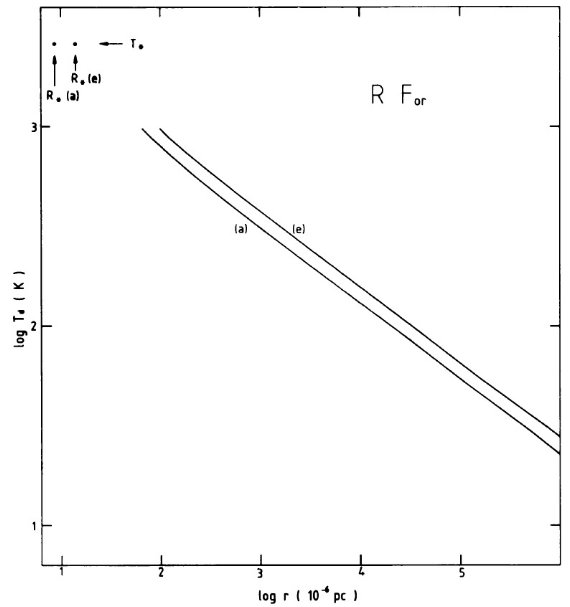 図4.星中心距離 r によるダスト温度の変化。a = 1983 年 9 月。 e = 1985 年 9 月。 |
| R For の7位相 SED のモデルを作った。 Jura の λ-1.3 オパシティ則とダスト凝結温度 980, 星の有効温度 2600 K を固定した。 τ1 = 0.68 - 1.2 となった。 | Lmax/Lmin = 2.3 であり、Rc,min/Rc,max = 1.5 である。⟨L⟩ = 104 Lo である。 1983 年極小の異常な暗さは極小時光度が (1/2)⟨L⟩ と低かった結果と解釈される。 |