Bolometric Corrections for Cool Giants Based on NIR Photometry

　アブストラクト　

　２．データベース　

　３．結果　

　３．１．BK_K 対 (J-K)　

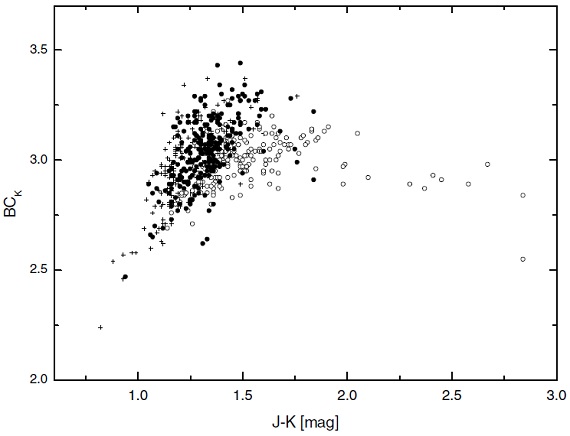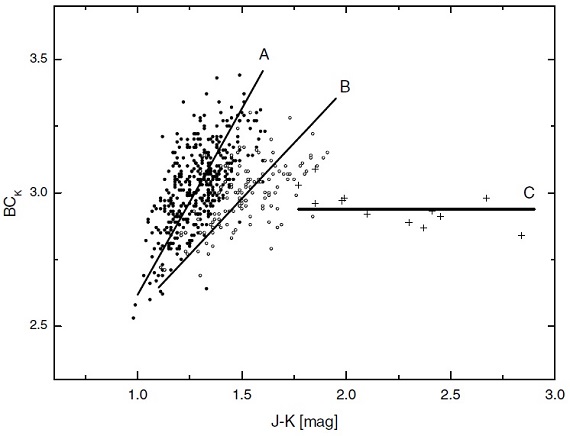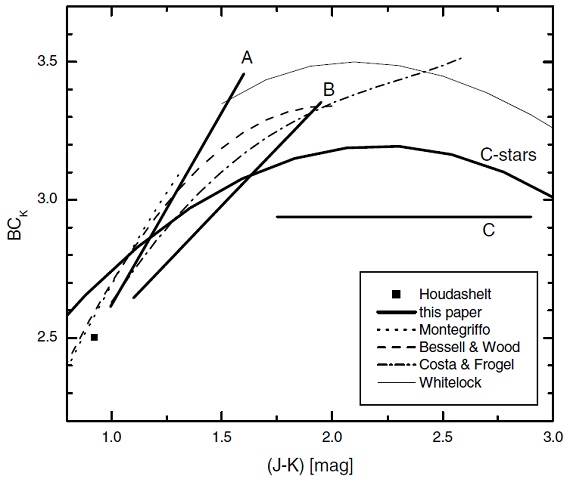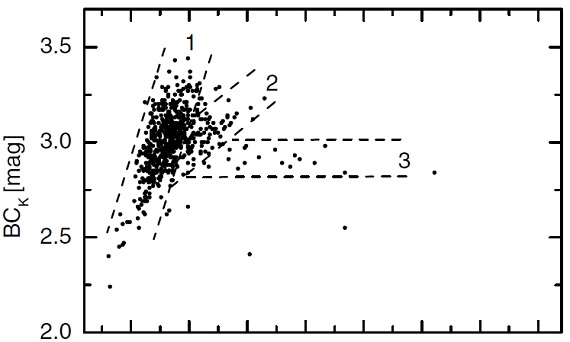
図１a．輻射補正 BCK 対 (J-K). スペクトル型 K, M. 　 　副構造３　 　図１a には BCK = mbol - K と (J-K) の関係を K-, M-型星に対してプロットした。図上には 1, 2, 3 の副構造が見える。 それらの勾配は 2, 0.5, 0 である。副構造間の重複もかなり大きい。 ただし、(J-K) > 2.2 では全てのサンプル星が副構造３に属する。した がってそこでは K 等級が mbol の良い指標となる。 副構造３の星は全てが二つの黒体成分を有していた。しかし、二黒体星は 図１の全体にわたっている。 　　 　炭素星の BCK は J-K = 2 まで単調に増加して行く。その先 では傾きが逆向きになって行く。そこで全体を二次式でフィットし、 　　BCK ＝1.70 + 1.35 (J-K) - 0.30 (J-K)2 を得た。 　L-ratio 　 　SED フィットから L-rati = Ldust/Lstar が計算できる。 単一黒体でフィットできた137 星はここでは考慮しない。 我々は L-ratio を三つのグループに分けて図２にプロットした。

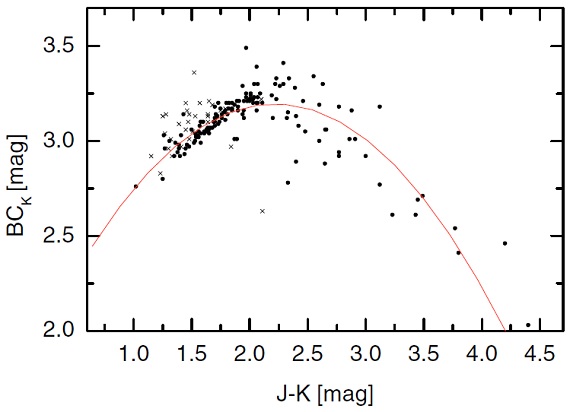
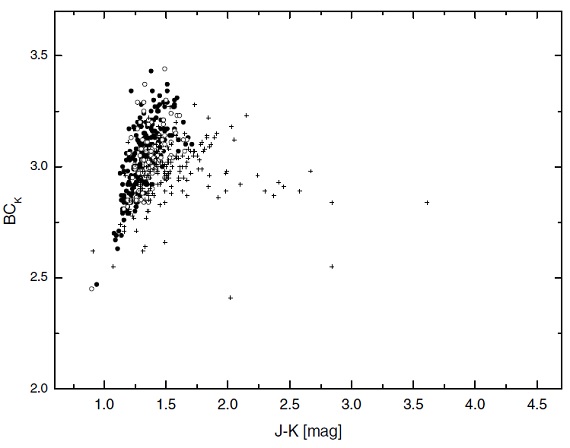
図１b．輻射補正 BCK 対 (J-K). スペクトル型 C. 図２．O-リッチで、２黒体SED の星に対する輻射補正 BCK 対 (J-K). 黒丸＝L-ratio<0.13. 白丸＝ L-ratio {0.013, 0.025]. 十字＝L-ratio≥0.025.

　３．２．その他の関係　

図３．O-リッチ星に対する輻射補正 BCK 対 (J-K). 黒丸＝Irrs. 白丸＝ SRs. 十字＝Miras. 　変光タイプ　 　図３にスペクトル型別の BCK 対 (J-K) 関係を示す。 副構造3 にはミラ型星しかない。しかし、ミラ型星は他の領域にも 分布するので、１対１対応ではない。 　失敗　 　以上の結果、光球とダストシェルの２成分分解では、輻射補正を 表現する助けとして不十分であることがわかった。2MASS による J,H,K データも助けにならない。 　別の分類の必要　 　図４にはサンプル O-リッチ星の (J-K) - (K-L') 二色図を示す。 それらを K-L' で３区分に分け、A, B, C と名付けた。 　図５＝新しい分類　 　図５には A, B, C 区画の星の BCK 対 (J-K) 関係を示す。 互いの重なりが殆どなくきれいに分かれている。 グループ A は Bessell, Brett 1988 の固有カラーに良く合っている。 J-K = 1.3 の Ｍ５ カラー付近で K-L' が急上昇し始め、黒体ラインに 達する。これがグループ B である。グループ C は黒体に沿って赤くなる。 これはダストシェルの温度を表すのであろう。グループ B はその中間の 過渡的段階である。

図４．O-リッチ星の (J-K) - (K-L') 二色図。 白丸＝K0, K3, M1, M5 巨星の固有カラー (Bessell, Brett 1988) 図５．O-リッチ星の BCK 対 (J-K) 関係。図４の３区画 星が重ならない。

　３．３．他の関係式との比較　

表１．ＢＣ　の線形表示式。 　Bessell, Wood 1984　 　Bessell et al. 1998 モデルに基づく BC に近い。J-K < 2 はグループ A と B の作る三角形の中をを通過する。A, B を区別しなかったためではないか？ 　Costa, Frogel 1996　 　Aringer et al. 2009 モデルからの BC に近い。C-星のみ。J-K < 2 は グループ A と B の作る三角形の中を通過する。 　Montegriffo et al. 1998　 　J-K が赤い方でグループＡに近づく。グループ B に対してはずれが大きい。

図６．様々な BCK 対 (J-K) 関係の比較。 　Whitelock et al. 2006　 　C-星のみ。A, B グループの平均に近い。 　グループ C　 　グループ C に対する BC は過去の文献にはない。（ホント？）

　６．結論