|
DDO 中間帯域測光を G, K 型の 1200 星に行い、CN 強度異常と絶対可視
等級を導いた。予想された通り、CN 強度指数 δCN は [Fe/H] と相関
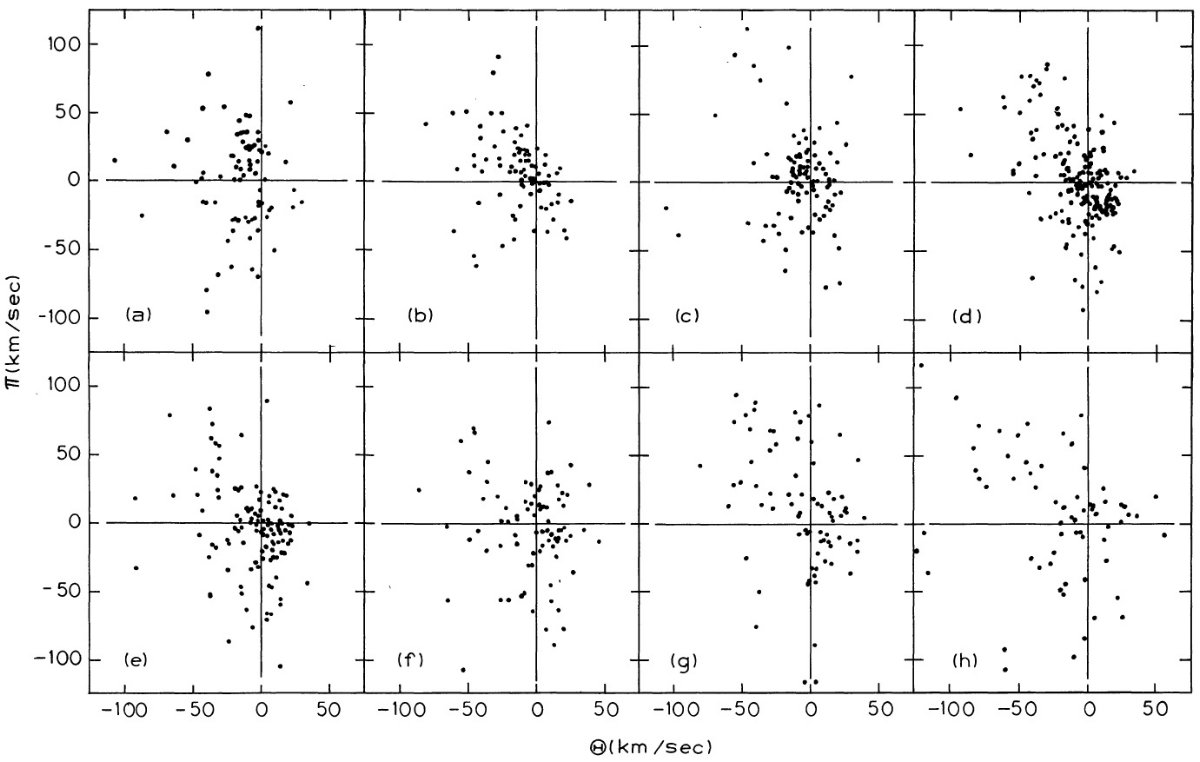
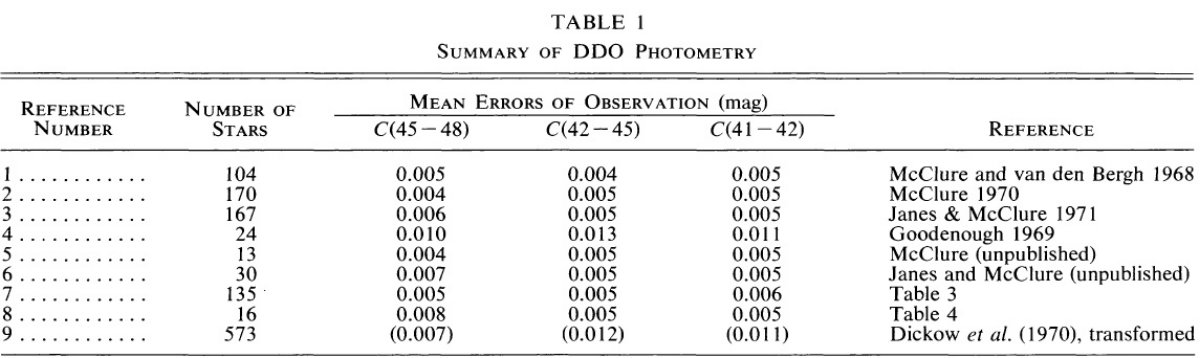
していた。一方、絶対等級の方は興味深い以下の結果を得た。 (i) K 線 絶対等級のウィルソン・バップ較正には修正が必要である。 (ii) δCN と Mv(K線) の間に相関はない。つまり、Mv(K線) にメタル依存性はない。 (iii) 新しい較正から出したヒアデス距離指数は (m-M) = 3.22 である。 | DDO 絶対等級に文献からの視線速度、固有運動を加えて 799 巨星の空間 速度を計算した。Z 方向速度は予想通り、δCN と相関がある。δCN が非常に弱い星は円盤上を高速で動いている。さらに、運動学から δCN には銀河系動径方向の勾配があるらしい。この勾配は銀河面上の 窒素の勾配を反映しているのであろう。 |
|
SMR 星 Spinrad, Taylor 1969 による SMR 星の発見以降、詳細な分光観測から、 このクラスの星は [Fe/H] が異常に高いというよりは、CN 吸収が異常に 強いと看做すべきと考えられるようになった。運動学的には SMR 星が 比較的古い種族に属している証拠がある。 |
G, K 型星の CN 強度と運動学特性 ここでは G, K 型星の CN 強度と運動学特性の関係を調べる。 これは銀河形成のモデルと 矛盾する結果である。主なデータは文献から得た視線速度、固有運動、 それに DDO 測光である。 DDO システムは CN 指数を含み、絶対等級も 得ることが出来るので適している。 |

データの出所を表1に示す。また、これまでに公表されていないデータを
表2に示す。今回新しくキットピークで観測した結果を表3に示す。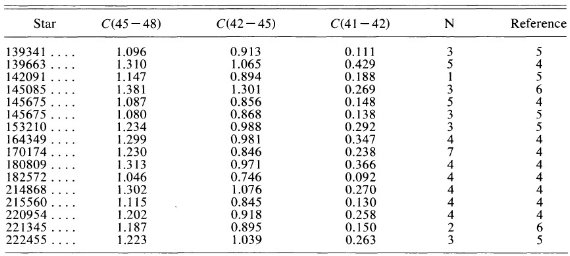 表2.これまで公表されていない観測 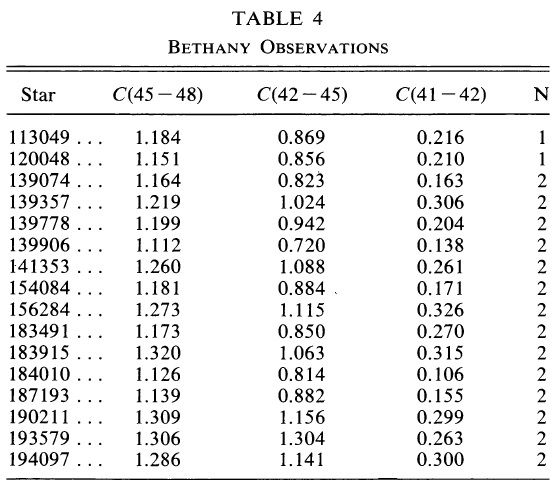 表4.Bethany 観測所の観測記録 |
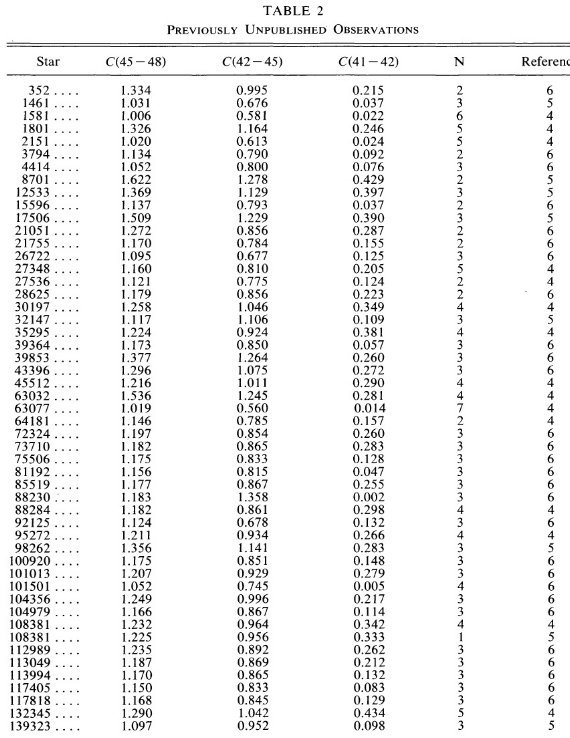 表2.これまで公表されていない観測 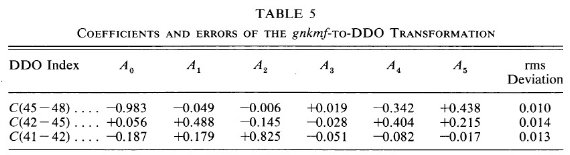 表5.コペンハーゲン gnkmf から DDO への変換係数 |
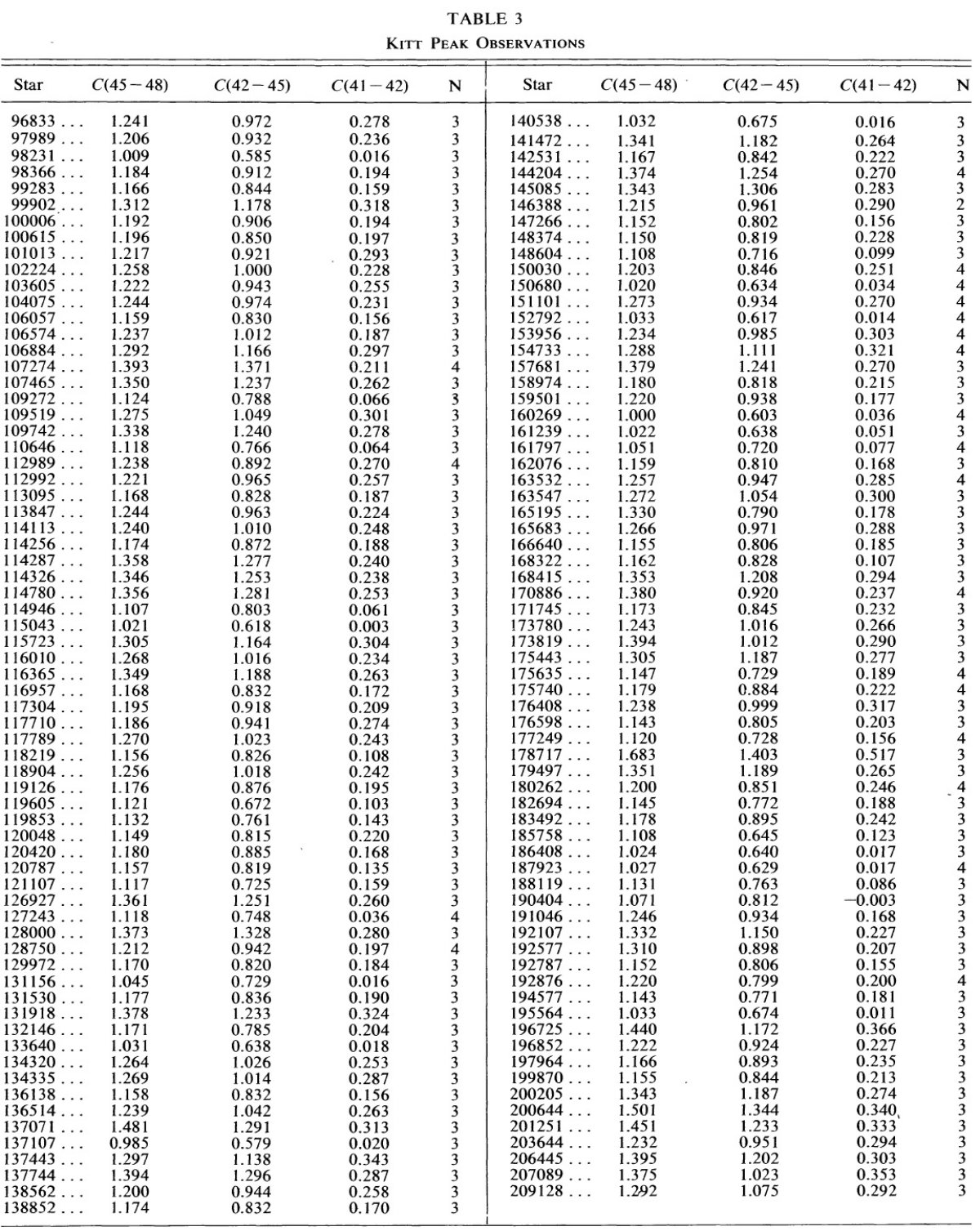
|
表6には DDO 測光と MK スペクトル分類を持つ較正用の星を示す。
これらは Ib 星意外 200 pc より近い。
C(41-42) と δCN C(45-48) と C(42-45) は有効温度と表面重力のよい指標である。そこで、 [C(45-48), C(42-45)] のペアに対して、標準的な C(41-42) を定めることが 出来る。対象星の C(41-42) とこの標準 C(41-42) との差が CN 強度異常で、 それはメタル量の指標となる。 標準 C(41-42) マップの作成第1段 (1)MK スペクトル型のある星を、スペクトル型・光度クラスの区画に分けて、 各区画毎に3つの DDO カラーの平均値を計算する。この平均値から二つの グラフを作る。図1は [C(45-48), C(42-45)] 面上に光度クラスをプロットしたもの、 図2は [C(41-42), C(42-45)] 面上に光度クラスをプロットしたものである。 図1にはスペクトル型情報も加えた。 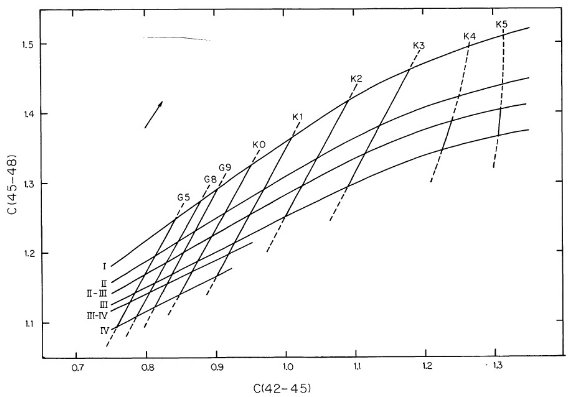 図1.[C(45-48), C(42-45)] 面上での平均光度クラスとスペクトル型。 矢印= E(b-V) = 0.1 に対応する赤化線。 |
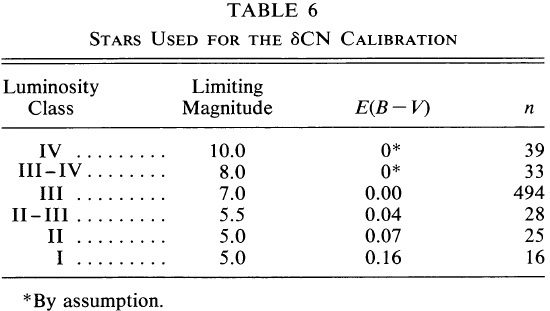 表6.δCN 較正に用いた星 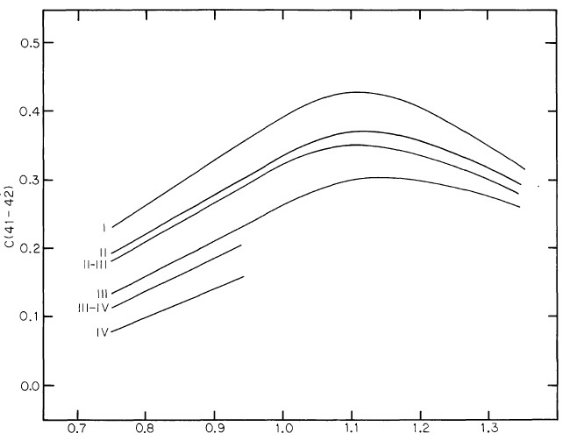 図2.[C(41-42), C(42-45)] 面上の平均光度クラス。矢印=赤化線。 |
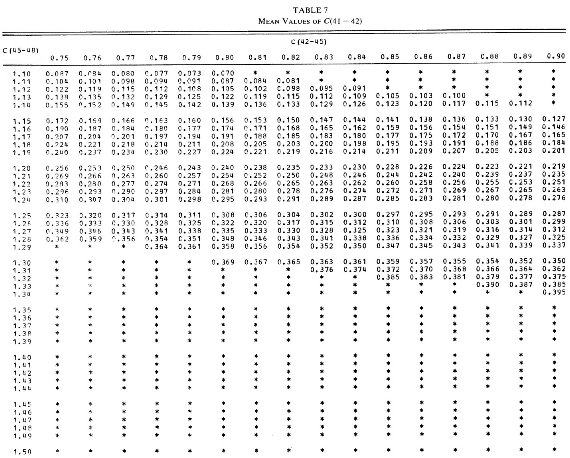
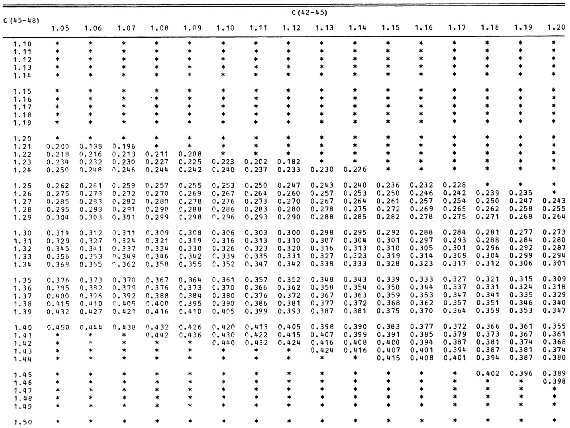
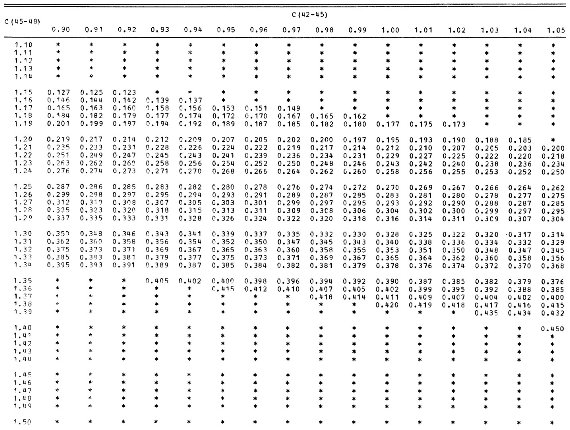
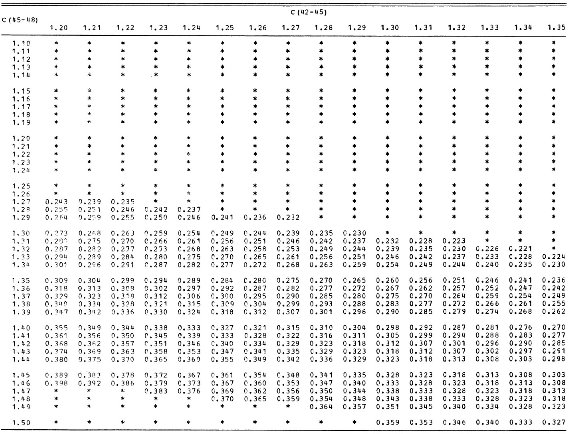
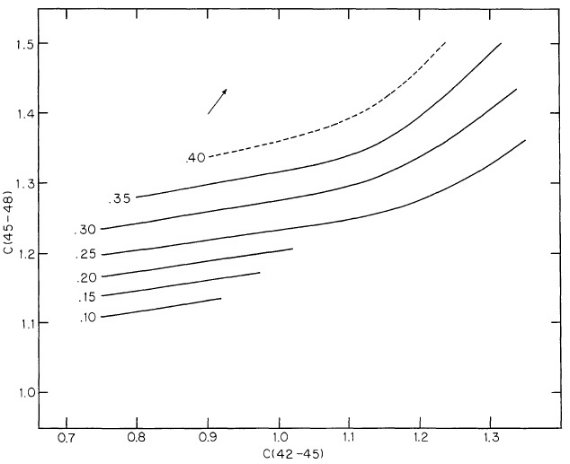 図3.[C(45-48), C(42-45)] 面上での標準 C(41-42) ライン。矢印は赤化。 C(41-42) = 0.40 ラインはデータ星の赤化のためやや不確か。 第2段 図2を用いて、C(41-42) と 光度クラスのペアに対して C(42-45) を探す。 次に [光度クラス、C(42-45)] ペアが図1を用いて対応する C(45-48) を定める。こうして選んだ C(41-42) に対して [C45-48), C(42-45)] 面 上に C(41-42)av 一定の線が引ける。 δCN 図3は C(41-42)av 一定線を示す。表7にはそれを数値で示してある。 ある星の C(41-42) が与えられた時、 δCN = C(41-42) - C(41-42)av δCN は McClure 1970 の δCm 指数と関係が深い。二つの指数は クラス III 星に関しては同一である。しかし、他の光度クラスでは異なる 定義を持つ。どちらも与えられた [C(45-48), C(42-45)]ペアに対する「標準」 C(41-42) からの差で定義される。したがって、両者の差は「標準」値の 定義の問題である。 |
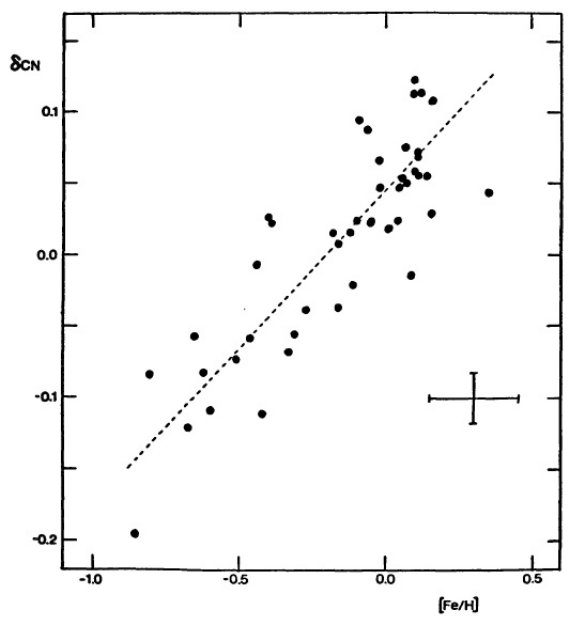 図4.Osborn 1971 リストにある 44 星の δCN と [Fe/H] の関係。 破線は平均線。 メタル量 図4の破線を式で表すと、 [Fe/H]DDO = 4.5 δCN - 0.2 (2) となる。個々星の [Fe/H] 精度は 0.10 - 0.15 であり、δCN から発生 する [Fe/H]DDO 精度は 0.07 あるので、式 (2) の信頼度には やや問題がある。 δCN は元来 C と N の存在量に関係する。子午線還流による C, N の増加の可能性も指摘されている。 |
  |
  |
|
ウィルソン・バップ効果 ウィルソン・バップ効果は G, K 型星に対し最も大きく、無矛盾な データセットを用意している。K 線の emission reversal log Wo 可視絶対 等級は次の式で与えられる。 Mv(K) = -14.94 log Wo + 27.59 (3) 現在 北天の 250 星の Mv(K) が測られている。内 179 星は DDO システムの データがある。これらから Mv(K) と Mv(DDO) の関係が調べられる。 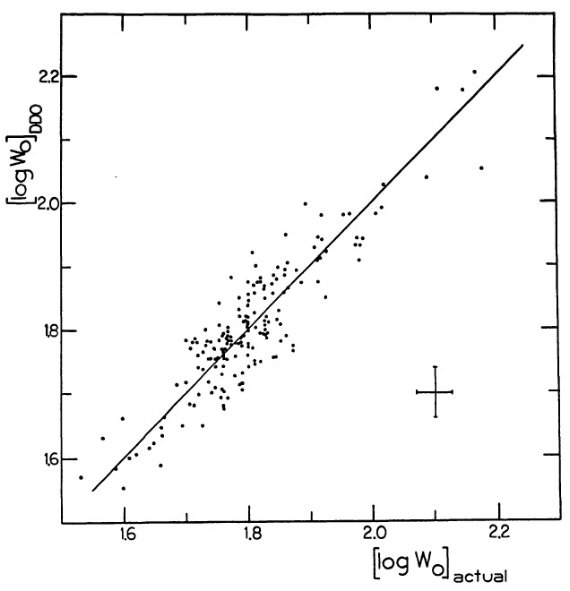 図5.log Wo と DDO 測光から逆算した [log Wo]DDO との 関係。直線は勾配1に設定。 |
log Wo と 三角視差から導いた Mv との関係 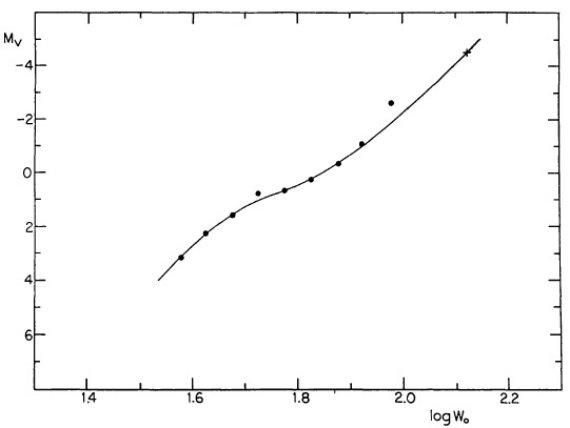 図6.log Wo と 三角視差から導いた Mv との関係= ウィルソン・バップ効果の新しい較正。 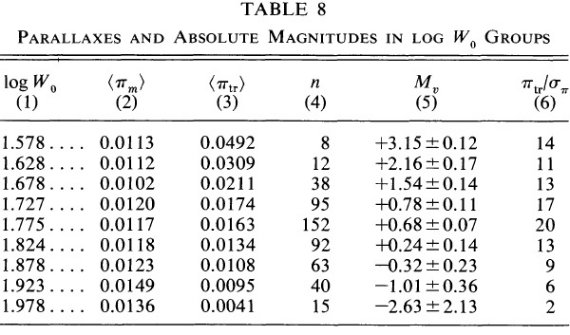 表8.低 Wo グループの視差と絶対等級 |
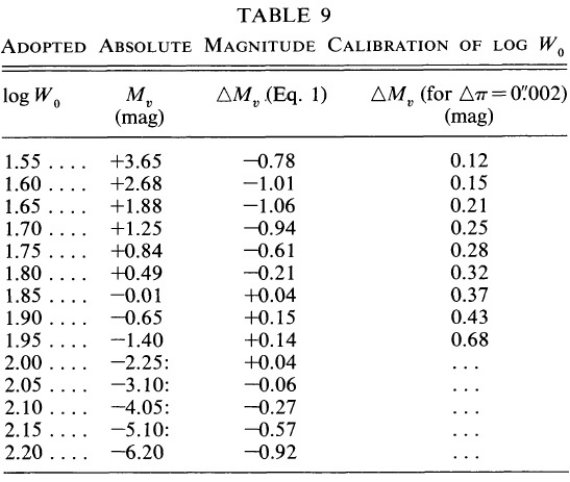 表9.log Wo と Mv の較正 |
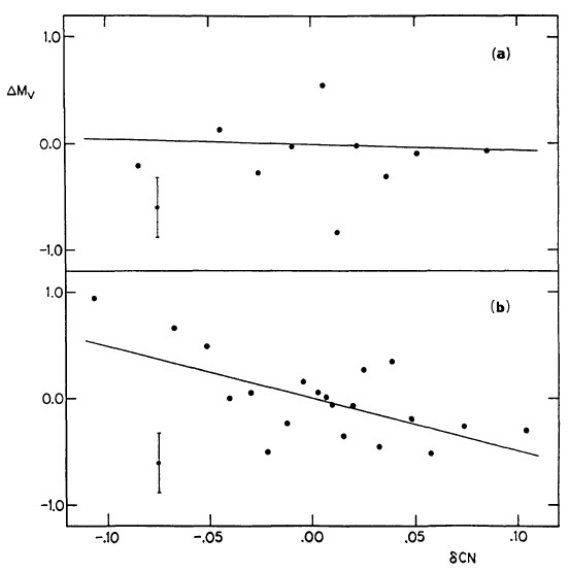 図7.(a): ΔMv = 分光絶対等級と三角視差絶対等級の差と δCN の関係。(b): 測光で決めた Wo からの絶対等級と三角視差絶対等級と δCN の関係。 |
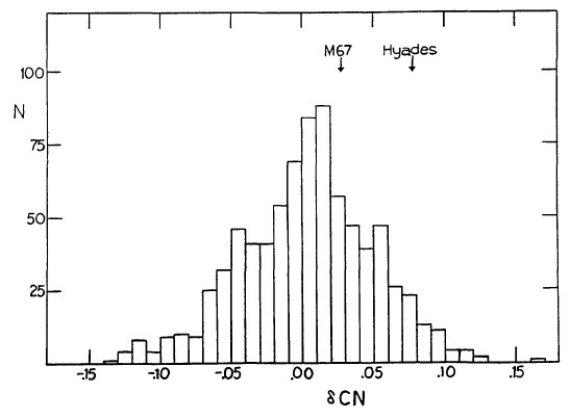 図8.δCN の分布ヒストグラム。比較のため、M 67 と ヒアデスの 位置を示した。 |
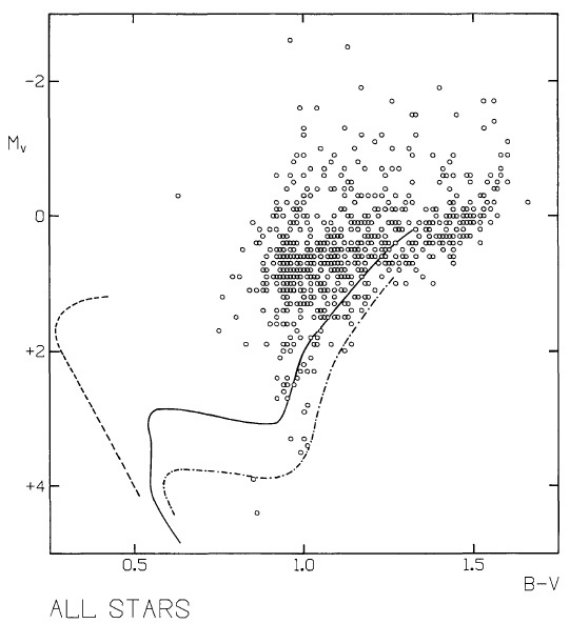 図9.B-V が公開されている星の CMD. 絶対等級は DDO 測光から計算。 破線=ヒアデス、実線 = M67, 一点破線= NGC 188 系列. |
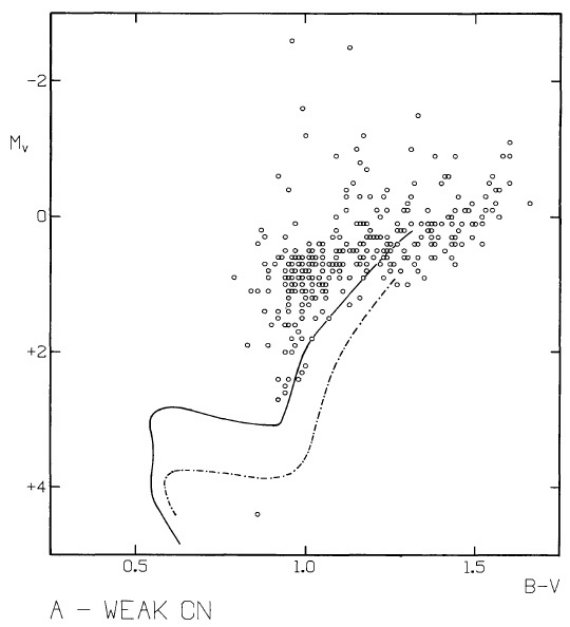 図10a.弱い CN 星の CMD. 実線= M 67, 一点破線= NGC 188. 二つの線の間に弱い CN 星がないことに注意。 |
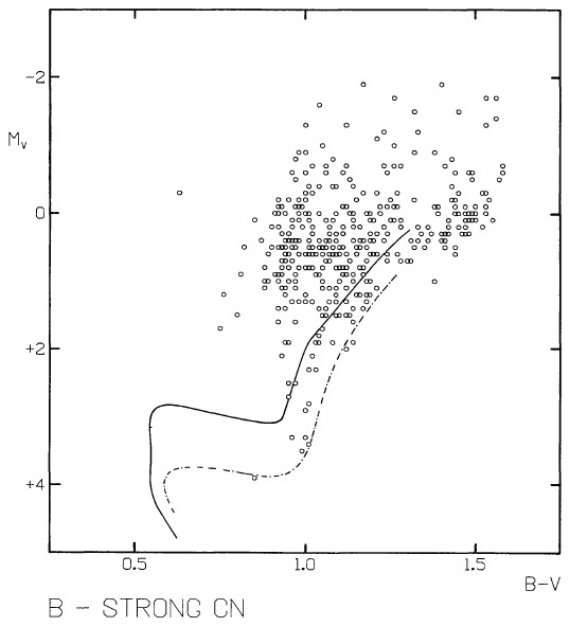 図10b.強い CN 星の CMD. |