Extended dust shell of the carbon star U Hya observed with AKARI



　
炭素星へ

アブストラクト

Context 　小中質量星はＡＧＢ期に激しいマスロスを行い、それは進化を左右すると考えら れている。星間空間に失われた物質は星周シェルを形作る。

Aims 　この論文では、あかりのFISUで撮った Hya　の　FIR像を示す。目的はシェルの 質量分布からこの星の過去のマスロス史を明らかにすることである。

Methods 　観測は FIS slow scan 65, 90, 140, 160 μ で行われた。画像サイズは 10' × 40' である。

Results 　FIS 像は丸いリングを示し、分離球殻状シェルを示唆する。中空シェルモデルは 内側半径 R=104"±3", half-mass thickness ΔRhm =16-23" ,ΔRhm/Rin=0.2 で、 密度分布のパワー指数は1.10-1.15 である。シェル中の　ダスト質量は(0.9-1.4) ×10-4(&kai;/25)-1M๏ である。 		パワー指数の制限は一意ではなく、-4.5 から +7 まであり得る。ダストマスロス 率は、(0.9-1.4)×10-4(&kai;/25)-1M๏ yr-1. 他のしっかりした値が指数則分布に対して決まった：ρ(118")= (1.8-2.4)×10-24(&kai;100/25)-1g cm -3 シェルの中心は星に対して約 9"(PA∼-85°)ずれている。また、シェル 内部星の北と南に放射光超過があるが、ＡＧＢマスロス初期に球対称マスロスからの 逸脱があった証拠かも知れない。PA=-70°, 距離5'の超過は多分ＩＳＭの ラム圧で剥ぎ取られた wake であろう。

Conclusions U Hya のダストシェルは星から分離して、球形である。有効巾は FIS の空間分解能 より狭い。これは熱パルスの直接的な結果か、２−星風相互作用か、停止ショックか、 それらの複合かも知れない。光学および遠赤外のサイズの違いは形成過程について 何かを示唆しているのかも知れない。何だ？

１．イントロ

　AGBマスロスの時間変動を示す観測が多数ある。例えばIRC+10216 (Grow 1997,1998, Mauron,Huggins 2000) マスロス変動を星の物理量変化に結び付けられるとマスロス メカニズムの理解へのカギとなるかも知れない。熱パルスはマスロスにかなり影響する と予想されている。(Vassiliadis,Wood 1993)

　特に遠赤外は遠方の 104 年以上昔に放出され、電波分子線では 追えない遠方のマスを観測できる。広がったダストシェルは星周ガスが星間空間に 入っていく作用域だが(Rowan-Robinson et al. 1986, Young et al. 1993, Libert et al 2007)、van der Veen,Habing 1988 はマスロスの不連続性を示唆した。 Willems, de Jong(1988), Chan,Kwok (1988) は IRAS 12-25-60 μ 二色図上で AGB星の分布をモデル化した。特に60μ超過の大きい星は激しいマスロスが熱パルス で中断され、現在低マスロスの可視炭素星の周りに分離シェルとなっているという シナリオを提案した。

　分離シェルはOlofsson et al 1988, 1990 によりＣＯ線で発見された。 幾つかの広がった、多分、分離シェルが遠赤外で実際に分離していることが確認さ 		れた。 (Waters et al 1994, Izumiura et al 1996, 1997) 理論面でも熱パルスAGBからの マスロス(Steffen et al 1998, Steffen,Schonberner 2000, Mattsson et al 2007), 星風と星間物質との作用(Villaver et al 2002, Wareing 2007)が研究された。スピツ アーやあかりのような衛星は冷たい広がったシェルの観測を推進した。

　この論文では、あかりによる U Hya の遠赤外観測結果を報告する。この星は V=5.4, ΔV=0.5, P=450 d の SRb である。マスロス量は 1.2 ×10 -7M๏/yr で、　v=6.9 km/s である。(Olofsson et al. 1993) 9Tc が検出されるが、この半減期は２０万年でｓ−プロセスで 作られる。したがって、この星は過去２０万年以内に３ｒｄドレッジアップを経験し たと考えられる。

　U Hya はIRAS の　Small Scale Structure Catalog　に載っており、Waters et al 1994 により、半径3 × 1017 cm (120")のリングが検出された。 この論文では U Hya のあかりＦＩＳ観測による結果を示す。

２．観測

まず、過去の観測のまとめを下に載せておく。


　ＦＩＳ観測は 65, 90, 140, 160 μ で行われた。ビーム幅は　各波長で FWHM = 37", 39", 58", 61" である。

３．解析と結果

　３．１．イメージ、フラックス　

図１　U Hya のあかり画像。左から N60, Wide-S(90), WIDE-L(140), N160。
　　　画像サイズは8.8'×24'、ピクセルは15"(N60,Wide-S),30"(Wide-L,N160)




　スロースキャンで撮られた画像(8.8'×24')を右の図１に示す。中心の点源は N60、WIDE-SでFWHM=40"、N160,WIDE-Lで60" である。広がった成分は半径が 約4' で、WAters et al 1994 が得た3.5'　と合致する。広がった成分の 最も明るいところはWIDE-Sで中心星ピーク値の1/5くらいである。また、N60 と WIDE-S では 100" 付近に輝度極小帯があり、明らかな円環状を呈している。

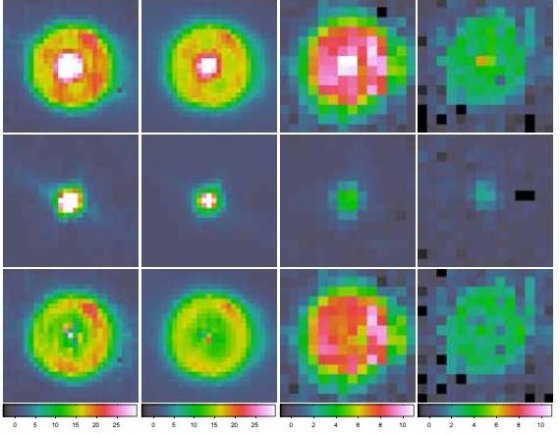図２　上段：分解前、中断：点源、下段：広がった成分


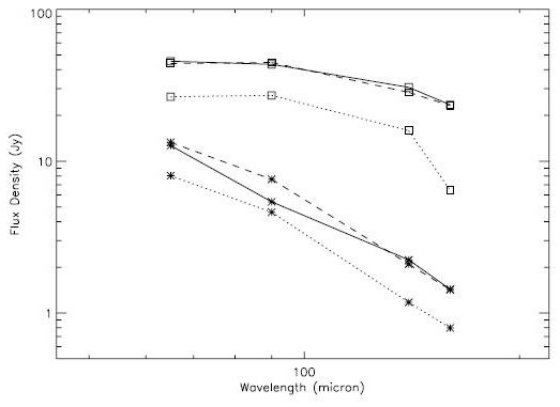　図２には元画像を点源と広がった成分に分けた結果を示す。大きさは8'×8' である。点源像はβ Peg(N60, Wide-S) とγGru(Wide-L,N160)を スケーリングして使用した。

　図３に点源と広がった成分のＳＥＤを描いた。中心天体の方が高温であることが はっきりと分かる。
図３　点源と広がった成分のＳＥＤ



　３．２．モデル解析　

　モデルは、点源の中心星＋球対称ダストシェル、と考える。まず、シェルの中心 を決める。半径80"から130"の間でシェル中心位置をずらしながら、等輝度線における データ点の分散を最小にする中心位置を求めた。意味は 良く分からない。　N60, Wide-S では、シェル中心は星から、0.6ピクセル右、 0.2ピクセル下であることが分かった。これは9.5" の差に相当する。ただしその方向は 固有運動とは一致しない。この解析ではこの差を無視し、４−２節で論じる。

　３．２．１．モデル　

　分離シェルモデル(Izumiura 1997)を使う。ダスト温度は星の光と熱平衡にあり、 シェルは全波長で光学的に薄いとする。Young,Phillips,Knapp 1993b によるとAGB星の 周りのダスト温度は距離 0.5 pc までは星の光で決まる。そこで仮定を、

　　　　　　　　　ρ(r) = ρ0 (r/r0)-α
　　　　　　　　　κ(λ)=κ0(λ/λ 0)-β

と置くと、Sopka et al 1988 より、

　　　　　　　　　TD(r) = T0 (r/r0) -2/(4+β)

　実際の解析では、上の分布とあかり点源関数(APSRF)との折り込みを取ってデータと 較べる。APSRF は近似的には二つのガウシアンの重ね合わせである。

　３．２．２．固定パラメター　

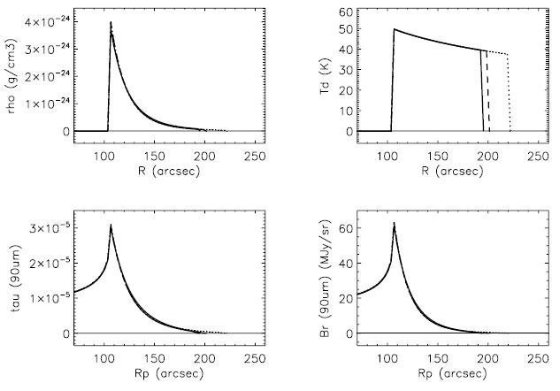
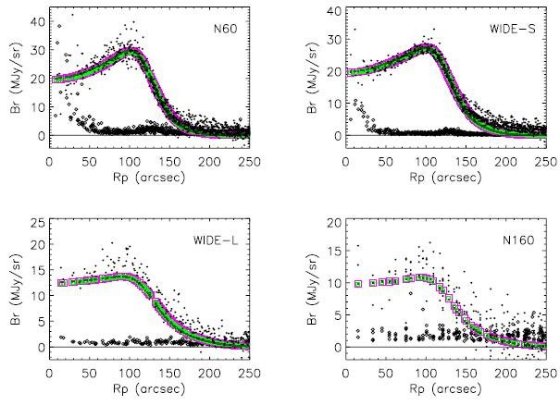
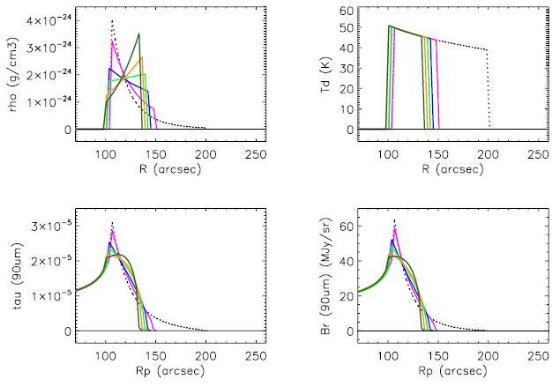
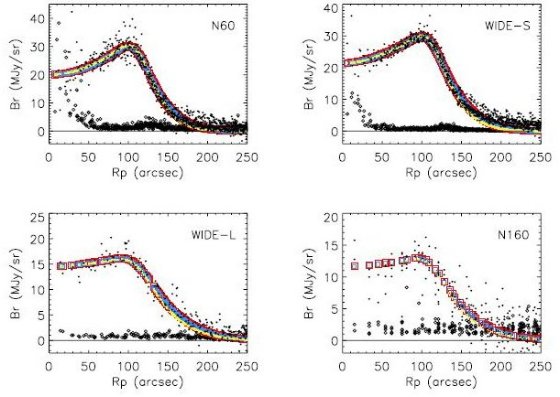
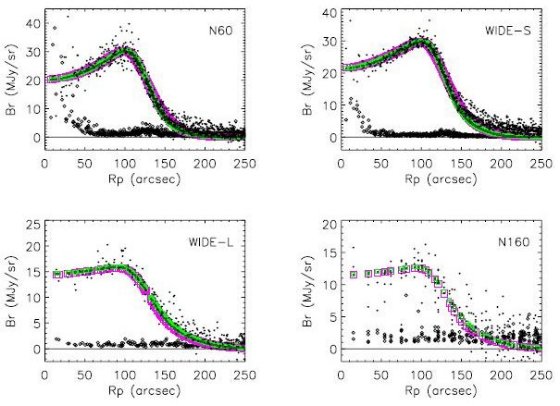
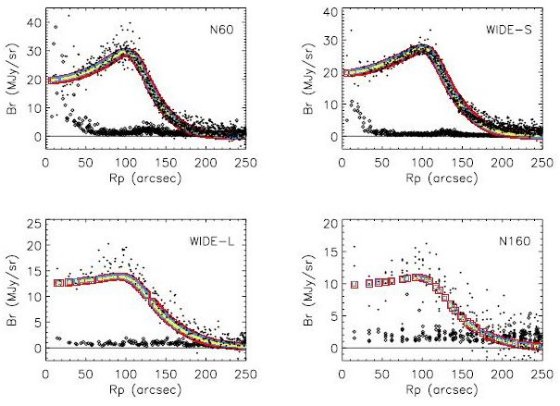　U Hya の距離を改訂ヒッパルコス(Leeuwen 2007)から162 pc ととった。中心星は 温度2800 K黒体輻射とした。Tsuji 1981は　Te = 2825 K、Groenewegen 		図４　シェルの輝度分布。





1992 は 2730 K としている。輻射等級(Gro.1992)と距離から、光度は 2960 L๏ となる。 　オパシティは 100 μ で 25 cm2g-1 (Hildebrand 1983) を採用した。もっと高い値（Drain 1981, Nakada 1988, Gronewegen 1998) も 出されている。

　３．２．３．フリーパラメター　

　モデルは５つのフリーパラメターを含む。それらは、Rin, ΔR, α, β, ρ である。

　Toは中心星の有効温度と光度、β, Rin から決まる。中心黒体 光源から期待されるフラックスを観測値と共に下の表２にまとめた。
表２　U Hya からの観測フラックスと黒体光源のフラックス。

　観測されるフラックスは計算値より大きいだろう、と言うのは現在進行中の マスロス雲からの放射が点光源には加わるからだ。 観測フラックスは分離シェルなしの10-7Mo/yr 星ＳＥＤと同じか？

表４　シェルのベストフィットパラメター。


　３．２．４．フィットの結果　

　χ2 = ∑r1<r<r2[(Bobs- Bmodel)/Eobs]2/(n-5) を最小にする フリーパラメターを探した。ここでBはピクセルフラックス、Ｅはエラーである。 表４にベストフィットのパラメターを載せた。Rhm は Rin から測ってシェル質量の半分に達する巾である。　パラメター中 Rin と β は比較的よく決まる。得られた値の Rin = 107" は Waters が IRAS で得た 105" とよく合う。また、 β = 1.15 の値は Jura(1988) が炭素星に得た 1.1 に近い。Nakada, Hildebrand, Le Bertre らも近い値を得ている。

　残りのパラメターもかなり良く決まった。α が大きいのはシェルが鋭い 壁を持ち、巾が狭いことを示す。ただ、問題はシェルの有効巾ΔRhm がピクセルサイズより小さいため、色々な(α, ρ0)の組み合わせが 同じくらいの　χ2 を与えることだ。

　ΔR, と α は PSRF の最も広がり、最も弱い成分に強く影響を受ける。 その表現として二つのガウシアンの重ね合わせは不十分である。フィッティングを 施す領域にシェル外側部を含めると、PSRF にはそんなに広がった成分が含まれてい ないので、大きな α と（または）大きな　ΔR に導かれる。この状況は 我々が最も狭い環状帯 (60", 140") でフィッティングを行った時にはっきりと 現れた。と言うのはそこでは PSRF の弱い部分が一番効かないからである。

　下の表５では環状帯 (60", 140") に対し、幾つかの固定した ρ0 で決まる α を載せている。 α が -4.5 から 7.0 まで変化しているが 　χ2 にあまり変化のないことがわかる。また、Mdust は安定して いる。これはMdustが基本的にフラックスに比例し、温度依存性が比較的小さい からである。ダスト温度はベストフィットモデルで 40 - 50 K であり、これは フラックス比 Br(65μ)/Br(90μ)∼1 にβ=1.1 の変形黒体輻射を 適用して得られる 49 K と合致する。




図５　上：　図４シェルの密度、温度分布。
　　　下：　光学的深さと輝度分布（折り込み積分前）



　　　　　　　　　表５　最も狭い環状帯(60", 140")でフィットして得たパラメター


図６　表５シェル(α=-4.5,0.5,4.5)の輝度分布。

図７　上：表５シェル(α=-4.5,-2.5,0.5,1.5,4.5)の密度、温度分布。
　　　下：光学的深さ、輝度分布。点線は表４ベストモデルのライン。
　よりよいフィットを求めて　

　 　ΔR, α, ρ0 の信頼できる値を決めるには、 （１）もっと良い空間分解能、（２）PSRF の裾野の値を良く決めること、と （３）シェル周辺部の高いS/Nの画像が必要なのである。

　これまでの解析から、もし N60 を 10 % 下げるか、WIDE-S を 10 % 上げるかする と χ2 が　(60"-140") で 6.01 から 4.88 へとかなり下げられる ことが

分かった。これは図２に見られるようにＳＥＤが　90 μ にキンクが見ら れることからもっともらしい。もし、ＳＥＤが滑らかであることを期待すると、 点源も広がった成分もWIDE-S(90μ)で　10-20 % フラックスが不足する。

　そこで、 WIDE-S(90μ) を 10 % 上げた画像に対して、ベストフィット探しを 行った結果が 表６，７と図 8，9, 10, 11である。解はかさ上げなしの時と似ているが 今回は β = 1.1 で Jura と同じになった。 χ2が下がる結果、解がユニークに決まるのか、 やはり皆同じようなのか？

　　　　　　　　　表６　WIDE-S10%かさ上げでフィットして得たパラメター



　　　　　　　　　表７　WIDE-S10%かさ上げで(60", 140")にフィットして得た パラメター





図８　表６のWide-Sかさ上げシェルの輝度分布。




図１０　表７のWide-Sかさ上げシェル(α=-4.5,-1.0,3.0)の輝度分布。

図９　表６のWide-Sかさ上げシェルのτと輝度。




図１１　上：表７Wide-Sかさ上げシェル(α=-4.5,-1.0,1.0,3.0)の密度、温度分布。
　　　　下：光学的深さ、輝度分布。点線は表６α=-6のライン。

　３．２．５．マスロス　

　モデルから決まったダストマスは、1.1 ×10-4(χ 100/25)-1 Mū である。これは 総マス 10-2(χ100/25)-1(fgd /100) Mū に相当する。ここにfgd(≈200-800)はガスーダスト比で ある。得られたダストマス≈10-4Mū は 光学観測から得られた 2×10-5Mū (Izumiura 2007) と近い。Gerard,LeBertre 2006 は２１−ｃｍ水素線を検出し、 直径32', マス＝0.0055 Mū とした。このサイズは分離シェル と同じ天体と看做せないが質量は今回求めたものと近い。Young et al 1993 は シェルがはき寄せられた星間物質であると考えて、4 ×10-3 Mū という値を与えた。ただし、彼らは距離＝２９０ｐｃ と考えていたので、マスを(1/1.8)にする必要がある。そうなると、このモデルで 説明するにはマスが地位さ過ぎることになる。

　我々が見つけた大事なことはシェルマスの半分は巾16"-23"という狭い

シェル に閉じ込められていることである。これはシェルの性質を考える大事なポイント である。

　ダストロス率は(1.8-9.6) × 10-8(ve/15) (χ100/25)Mū/yr である。これは 総マスロス率に直すと、(1.8-9.6) × 10-6(ve/15) (χ100/25)(fgd/100)Mū/yr に なる。Waters et al 1994 の 5 × 10-6Mū/yr と合っている。

　もう一つ、パワー則ダスト密度分布に関し、ρ(118") = 1.8(2.4) × 10-24(χ100/25)-1 g cm-3 は図７，１１から見られるように安定した値である。

三角型やガウシアンの密度分布も似たような χ2 を与えることを 注意しておく。

４．議論


　４．１．分離シェルの起源　

　Rowan-Robinson 1986 は IRAS 100 μ 超過放射は星風が星間空間物質と出会う 位置にいる分離シェルによると主張した。van der Veen と Habing 1988 はマスロス に不連続があると示唆した。

　Willems, de Jong 1988 と Chan,Kwok 1988 は炭素星で高いマスロス率時期が 中断されるというシナリオで IRAS ２色図上での炭素星分布を説明した。この説は 魅力的だが承認されているわけではない。広がった薄いシェルが炭素星のまわりで 発見されて(Olofsson et al 1988, 1990, 1993, Waters et al 1994, Izumiura et al 1996, 1997) 別の説が浮上してきた。次にそれらを検討しよう。

　４．１．１．熱パルスと２星風作用　

　Steffen et al 1998, Steffen,Schonberner 2000 はシェルの時間変化を計算した。 彼らは典型的ヘリウムシェルフラッシュがマスロスを発生させ、高速度星風を 短時間引き起こす事を示唆した。それは２星風作用（Kwok et al 1978）により 薄いダストシェルを産み出す。彼らは又、熱パルスの後、マスロス率が急激に低下し、 分離シェルを作り出すことを示した。

　Mattsson, Hofner,Herwig 2007 は輻射流体力学モデルにダスト形成と星風加速 領域を取り入れた計算を行った。彼らは熱パルスの結果マスの噴出が起こり、高速 星風となることが薄いシェルの形成に必要なことを示した。

　U Ant の場合　 　ある種の炭素星には分離分子シェルがＣＯで観測されている。(Olofsson 1996, 2000, Schoier et al 2005) U Ant の２重分離シェルの外側成分はダストの内側シェルと 一致する(Izumiura et al 1997) が外側ダストシェルには CO が検出されない ことを注意しておく。　シェルの数は３つ？　 ガスとダストの分離シェルのco-location は２星風作用のシナリオに合致する。 Schoier et al 2005 は、観測された薄い分離ＣＯシェルの解析から、 急激な高速マスロスが分子ガスシェルの原因である結論した。彼らは 10-7 M๏/yr の星風に １００年間続いた10-5 M๏/yr の星風が 襲いかかったと結論した。

　U Hya の場合　

　U Hya の分離シェルも U Ant（外側シェル） や Y CVn と同様に星風作用で 形成された可能性がある。ただ、そのどれも CO は未検出である。 Steffen,Schonberner 2000 はマスロス率が突然落下するだけで分離ダストシェル の形成に十分であり、全ての熱パルスが分離シェルを産み出すが、全てが はっきりした薄いガスシェル形成に適した性質を備えるわけではないと主張した。 これは薄い分子シェルの星から遠方での存在は星間紫外輻射場による解離 作用に強く依存するからである。これは、上の３つで分子シェルが存在しない理由 かも知れない。少なくとも U Hya の場合は 99Tc が検出されたこと から熱パルスが最近 105年内に起きたことは確実である。

　マスロス率とガスシェルの有無　また、CO が存在する星の現在のマスロス率は平均してより低い。 意味不明 CO が存在する星ではマスロス率が 10-7 M ๏/yr 以下だが、CO 不在星ではそれ以上である。熱パルス後マス ロスはいったん低下し、それから静謐水素殻燃焼状態でのマスロスへとゆっくり 増加していく。CO-不在の３つの星で現在のマスロス率が高いのは、前回の 熱パルス後の経過時間が長いことを意味し、それはシェルサイズが大きいことにも 現れている。

　銀河内の位置について言えば、シラス混入が大きいのは星間物質が濃いことを 意味し、それは大量の星間物質をはき寄せなければならないことで、沢山の 星間分子がシェルに取りこまれ、星周物質を解離から守る。。

　U Hya に関して分かった重要なことは、シェルが薄かったことである。 シェル内側半径 ∼ 100" と半質量厚みの２倍 < 50" から、シェルの 放出は 5000年から8000年まえにかけて起きたと評価する。 この３０００年は遅い星風の期間？それとも速い星風？

　ダストシェル膨張速度　 ここでは膨張速度 を 15 km/s と現在の U Hya のガス速度 7 km/s の倍としている。これは COが存在する分離シェルの速度を測ると現在星風速度より大きい場合が多い ことに合わせたのである。

　ガスとダストの結合　更に、ＣＯシェル に対応するダストシェルの位置が殆ど（全くではないが）同じである。これは ダストがガスと殆ど同じ速度で動いていることを意味する。 では、小さなずれがあったのか？あったらしい。小さなダストのズレ速度 が示唆されている。

　パルス間隔　 静謐水素燃焼期の U HYa の光度は (3-6) × 103 L๏ 程度である。太陽メタル量のMcore-L 関係(Boothroyd,Sackmann 1988 ApJ 328, 641)とMcore-パルス間隔関係(Boothroyd,Sackmann 1988 ApJ 328, 653)を使うと、 この光度に対するパルス間隔は (2-1) × 105 年である。 このパルス間隔は先に Tc から求めたこのシェルの年齢より一桁長い。この 関係はここで論じているシナリオに合致する。

　シェルのマス　 SS00 は、典型的な熱パルスシナリオでは、TT Cyg を例として、シェルサイズが (1-5) × 1017cm の時、分離シェルのマスは 0.007-0.01 M๏ であるとした。前に述べたが、 U Hya のシェルは長くても 3000(v/15km/s) 年 で、ダストマスにして 1.1 ×10-4(χ 100/25)-1M๏ , 総マスでは ∼ 10-4(χ100/25)-1M๏ である。すると、マスロス率は(10-6-10-5)M๏ になる。Mattsson et al 2007 のモデルでは中心星から 0.1 pc でのガス密度は 10-21 g cm-3 でダスト密度が10-24 g cm -3という U Hya の結果と合致する。

このように、熱パルスにより起こる高速星風と前の星風による２星風相互作用 説はもっともに見える。


　４．１．２．終端ショックシナリオ　

　高速星風説の欠陥は Y CVn には Tc も、他の S過程元素もないことである。 Y CVn が熱パルスを経なかったという意味ではない。しかし、分離シェルは他の 方法でも形成されるのかも知れない。

Rowan-Robinson et al 1986 は幾つかの IRAS 天体で検出された 100μ 放射は 星風が星間ガスと出会う箇所のダストシェルから出ていると主張した。Young et al 1993 は過去のマスロス物質が星間ガスに抑え込まれて溜まっていると進化の進 んだ星の周りの広がったダストシェルを説明した。しかし彼らの結果は、U Hya のような 0.1 pc くらいの広がりでは星間ガスの影響はほとんどないことを 示している。

　Libert et al 2007 は　termination shock model により、適当な一定強度の マスロスにより Y CVn の拡がったＨＩシェルを説明した。このような拡がった ＨＩシェルは Villaverm Garcia-Segura,2002 により、熱パルスによる星風強度の 変化で過渡的なシェルが ∼ 20000 年くらいの寿命で形成されることを示した。 彼らによると、R ≥ 0.5 pc ではもはや密度や速度分布はマスロス史を反映 しない。ただし、　U Hya シェルのような　0.1 pc くらいではマスロス史を なぞっている。

Gerard, Le Bertre 2006 は　26 星でＨＩを検出した。U Hya からの HI は 32' 直径に広がっていた。これはダストシェルの８倍の大きさである。 HI ガスが遠赤外で見えるダストシェルと直接つながっているわけではない。 ただ、もしかすると、彼らが見たのは西向きの星間風によりたなびいている シェルのガスを見ているのかも知れない。

　質量収支　

　このシナリオでは一定マスロスを仮定する。シェルを次の３つに分ける。

（１）内側の乱される前の一定マスロス星風

（２）圧縮された星風

（３）圧縮された外側物質。（星間物質,RGB星風,数サイクル前のAGB星風）

（１）と（２）の間には termination shock が、（２）と（３）の間には contact discontinuity が存在する。（３）の外側はバウショックで区切られる。

tFORM 昔に現在の一定マスロス率が開始されたとする。Rin=シェル 内側半径,　Rout=シェル外側半径, V = 風速、ρout= （３）での密度, M '=マスロス率とすると、 初めに Rout 内にあった（３）物質は全て シェルに掃き寄せられたと考え

　　　Mshell　=　M '　(tFORM-Rin/V) + (4/3)π Rout3ρout

　Ivezic, Elitzer 1995 の式によると、一定の星風は周りのガスを寄せ集めてシェル を形成するが、それは tFORM　後である。

　　　tFORM ≈ 3.2 × 109(M ' /n/V3 )1/2 yrs

ここで、M ',n と V は(M๏/yr), (cm-3)と(km/s) 単位である。同様に、 contact discontinuity の位置は、

　　　rshell ≈ 1022(M ' /n/V)1/2 cm

これらの式の値は Young et al 1993 の与える値と一致する。Young et al 1993 によると、吟緯 l = 38 ° 距離 = 162 pc の当たりでは、銀河面から 100 pc の高さで　n = 0.7 cm-3, 銀河面で　n = 2 cm-3である。 この値を入れると、現在値 M ' = 1.2 × 10-7 M๏ /yr, V = 6.9 km/s に対して、

　　　tFORM = 7.3 × 104年、　　 rshell = rshell = 617"

である。これらの値は U Hya の観測値より大きい。ただし、rshell の 値は Gerard, Le Bertre 2006 が観測した HI のサイズに合致する。ただ、前に 述べたように HI サイズは大きめに評価されがちである。また、tFORM が想定されているパルス間隔のかなりの割合を占めてしまう。

　Rout = rshell = 1.6 × 1018 cm, Rin = 2.4 × 1017 cm (100"), ρout = 1.6 × 10-24 g cm-3 (n = 0.7 cm-3), tFORM = 7.3 × 104年 を代入して、

　　　Mshell = 2.1 × 10-2( = 7.4 × 10-3 + 1.4 × 10-2)M๏

を得る。この値は U Hya の分離シェルに対して我々が得た値とよく一致する が、観測されたダストシェルのサイズと予想されたガスサイズとの不一致は 無視できる大きさではない。 Gerard, Le Bertre 2006 は HI マスに, サイズ = 32 ' として、5.5 × 10-3)M๏、 M ' = 0.2 × 10-7)M๏/yr を与えた が、これは CO 観測から得られる現在のマスロス率 1.2 × 10-7) M๏/yr に較べるとかなり低い。

　サイズの不一致は ρout を高めて、tFORM と rshell を U Hya の観測値に合わせれば軽減される。n = 13 (前の１７倍！) にすると、rshell = Rout として、 rshell = 3.6 × 1017 cm, tFORM = 1.7 × 104年, Mshell　=　 3.7 × 10-3( = 7.2 × 10-4 + 3.0 × 10-3)M๏ を与える。シェルマスは まあまあ受け入れ可能な範囲である。高い n は以前のマスロスによるものと 解釈できる。

　このように、termination shock model では、通常の星間密度の一桁上の 値が必要とされるのである。

　４．１．３．シェルの可視像　

　U Hya のシェルは V バンドでも撮像されている。シェル外縁半径は 130" である。 可視画像はWide-S像とよく一致している。 N60 と Wide-S 像の PA = -7° に 存在する明るい模様は V バンドでも認められる。シェルの半ピーク輝度の半径は Ｖバンドで 127 ± 3", Wide-S で 135 ± 3" である。この差は V バンドの PSRF の FWHM が　5" に対し、Wide-S の PSRF の FWHM が　40" と大きいことが原因である。

　しかし、光度極大の時期には可視半径=115 ± 5"は遠赤外半径= 100 ± 5" より明らかに大きい。前の値との 関係が分からん。何で光度極大の方が小さいの？ この差の一部はWIDE-S の大きな smearing beam が原因である。smearing は ピーク位置を数秒角内側にずらすからである。それで残るのは約 10" となる。 このようなずれが実際に生じるのは密度分布が外側に向けて急激に増加する 場合である。図７、１１の下側のパネルで α = -4.5 のケースを 見て欲しい。シェルの縁が 130" なのはこの解釈を支持する。


　この様な密度分布は熱パルスに伴うマスロス率の変化をそのまま反映して いるのかも知れない。熱パルスの前はダストとガスは非結合で、ダスト密度は 低く、ダスト速度は速かった。熱パルスによる小爆発マスロスではダストと ガスは結合していて、ダストは高密度で低速度であった。熱パルス終了後、 ダストは再びガスと非結合となり低密度高速に戻る。このような様子は SS00 でも現れている。さらに、外側に密度が増加するモデルは termination shock にも 2 星風モデルにも現れる。どちらが妥当か決められない。

波長に依りシェル半径が変化することは大変おもしろく今後も追究する価値が ある。また、シェルの膨張は50年で　1" くらいに相当し、観測可能である。 バック散乱を使った分光法での視線速度測定も将来可能であろう。
　４．２．中心星位置のずれ　

　シェルの中心は星から見て、PA = -85° ± 12° の方向に 9.5" ずれている。U Hya の固有運動の方向は PA=+132° であるから、 もし静止星間空間の中を運動しているならずれは PA=-48° 方向になるはず である。ずれのずれ＝-37° は星間ガス流を示唆する。そうだとすると、 下流側に (PA=-85°）に　wake が発生するだろう。実際、WIDE-S像を 見ると図１２で PA = -60° から -80° 方向に輝度超過がある。 もっと良い観測が必要である。

　このようなずれは、R Hya(Hashimoto et al 1998, Ueta et al 2006), ο Cet (Ueta 2008), R Cas (Ueta et al 2010) で報告されている。 それらは形状からバウショックとされていて、U Hya と異なる。

５．結論　

（１）U Hya シェルの遠赤外直接画像が初めて取れた。フラックスが測られた。

（２）モデルフィットの結果、

　　　Rin = 104" ± 3" = 0.08 pc

　　　ΔRhm = 16-23", ΔRhm/Rin =0.2

　　　κ ∝ λ-β とした時、β= 1.10-1.15

　　　ρ ∝ r-α とした時、α= 6.0-7.0
　　　　　　　　　しかし、α= -4.5 to 7.0 が可能。

　　　Mshell ≈ 10-2 M๏

　　　M ' (Rin)=(1.8-9.6)×10-6(v/15)(25/χ 100)(fgd) M๏/yr
　　　　　　　　　現在のマスロス率より一桁上である。

　　　ρ(118")=1.8(2.4)×10-24(χ100/25) -1 g cm-3 はロバスト 		（３）分離シェル形成シナリオを較べた。
　　　　　熱パルスと高速星風モデルはもっともらしい。
　　　　　しかし、星間密度を一桁上げれば、termination shock も可能。

（４）　可視と遠赤外でダストシェルのサイズに違いがある。ダスト密度が外側
　　　　に上がれば説明可能。必ずしもマスロス率の時間変化ではなく、前に
　　　　述べたモデルでも可能。

（５）シェル内で星の南北に輝度超過。非球対称マスロスの萌芽か？

（６）シェル中心が星から 9" ずれる。星間風の影響


より高い空間分解能の観測が必要である。